一種質量塊-彈簧自參數共振壓電俘能器研究
陳忠成,解小東,謝 進
(西南交通大學 機械工程學院,四川 成都 610031)
0 引言
近年來,收集環境振動能量為微電子設備提供電能的俘能器研究越來越多[1-3]。其中,壓電俘能器因其結構簡單、能量密度高而備受關注[4-5]。
目前多數壓電俘能器是以直接激勵方式工作。但有研究表明,參數激勵比直接激勵更能產生高的響應幅值[6]。Daqaq等[7]建立了參數激勵壓電俘能器的集中參數模型,并在該模型中考慮了幾何非線性和慣性非線性。Abdelkef等[8]建立了參數激勵壓電俘能器的分布參數模型。Lan等[9]研究了帶末端質量塊的參數激勵俘能器的內共振特性。
參數激勵壓電俘能器存在的主要問題是激勵閾值高及工作帶寬窄。為了克服存在的問題, Jia等[10-12]通過引入一個兩端固支的水平梁作為直接激勵,提出了一種自參數共振的參數激勵俘能器,實驗證明,與傳統俘能器相比,該俘能器激勵閾值低,工作帶寬寬。Yan等[13-14]推導了自參數共振參數激勵俘能器的理論模型,進一步揭示了其工作特性及其原理。Yang等[15]引入了一個水平梁,通過直接激勵的水平梁和參數激勵的豎直梁間的磁耦合來實現降低激勵閾值及提高工作帶寬的功能。這些新型的自參數共振參數激勵壓電俘能器的結構設計均增加一個水平梁作為直接激勵,以此對激勵起放大作用,進而降低了參數的激勵閾值,提高俘能帶寬。實際上,水平梁的增加是為系統增加了一個新的自由度,但加大了俘能器的結構尺寸。
本文借鑒自參數共振的參數激勵壓電俘能器增加一個自由度以降低激勵閾值及增加俘能帶寬的思路,提出在壓電梁末端增加質量塊-彈簧的二自由度參數激勵俘能器,并對該俘能器發生參數共振時的激勵閾值與俘能帶寬進行分析和討論。
1 質量塊-彈簧壓電俘能器的結構及數學模型
1.1 質量塊-彈簧壓電俘能器的結構及其動力學方程
本文提出的質量塊-彈簧壓電俘能器的結構如圖1所示。該俘能器在參數激勵俘能器壓電梁的末端加裝一個彈簧和質量塊。當俘能器受到外界沿z方向上的振動激勵時,壓電梁在末端質量塊及彈簧的共同作用下發生參數共振。圖中,h為彈簧的高度,m0為末端質量塊質量,l1為壓電片距離地面的距離,ls為梁長度,bs為梁的寬度,hs為梁的厚度,lp為壓電片長度,bp為壓電片寬度,hp為壓電片厚度,z(t)為外界激勵位移。
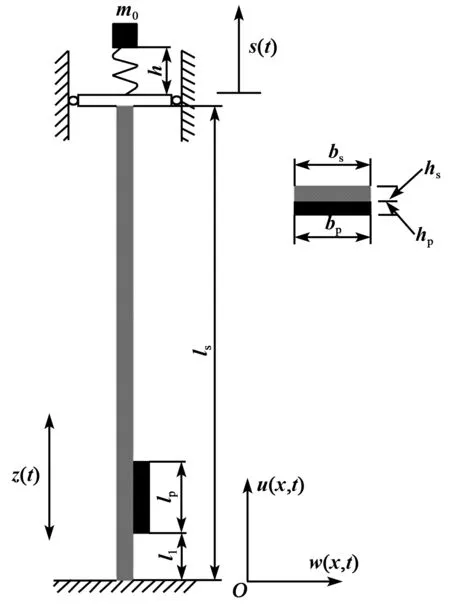
圖1 質量塊-彈簧壓電俘能器的結構
圖1所示結構與現有的一些參數激勵俘能器的主要區別是:本文提出的結構是在質量塊與壓電梁之間增加一個彈簧,相當于系統增加了一個自由度。本文假設壓電梁末端的滑動平臺的質量和彈簧質量都很小,可忽略不計,且彈簧為線性彈簧。
采用擴展哈密頓原理推導出俘能器的機電耦合數學模型。擴展哈密頓原理的表達式為
(1)
式中:q為壓電梁的廣義位移;s為末端質量塊相對于壓電梁末端的廣義位移;V為壓電片的電壓;t為運動時間;L=T-U-W為拉格朗日函數,T為系統的動能,U為系統的勢能;W為壓電片電勢能;δw為非保守力所做虛功的變分,且:
(2)
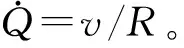
俘能器的動能為壓電梁的動能和末端質量塊的動能之和,即:
(3)
當梁足夠細長,假設梁不可伸展,梁的橫向位移和軸向位移間的關系為
(4)
俘能器的機械勢能包括梁應變的勢能、梁的重力勢能、末端質量塊的重力勢能及彈性勢能,則總機械勢能為
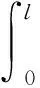
z(t)]dx+m0g[s(t)+z(t)+u(l,t)]+
(5)
式中:(′)為對位移求導;k為彈簧的剛度;s(t)為末端質量塊與壓電梁末端的間距;u(l,t)為壓電梁末端與地面的軸向間距;z(t)為地面上下振動位移;EI為梁抗彎剛度。
壓電片電勢能為
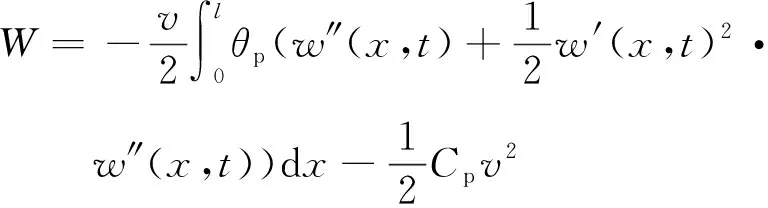
(6)
式中:θp為壓電片的機電耦合系數;Cp為壓電片的壓電電容。
為了得到系統的離散模型,假設一階振型占主導,壓電梁的橫向位移w(x,t)為
w(x,t)=φ(x)q(t)
(7)
式中:q(t)為只與時間相關的廣義位移;φ(x)為該系統的模態函數。對于兩端固支的邊界條件,模態函數為
(8)
將式(3)、(5)、(6)代入式(1)可得到質量塊-彈簧壓電俘能器的機電耦合方程:
(9)
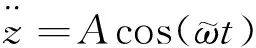
為了對比分析質量塊-彈簧對壓電俘能器俘能特性的影響,式(9)中令k=0,可得無彈簧的壓電俘能器,即現有的一些壓電俘能器的動力學方程為
(10)
1.2 質量塊-彈簧壓電俘能器的系統參數及動力學性能
本文中取壓電俘能器的系統參數及幾何尺寸如表1所示。表中,Es、Ep為楊氏模量,ρs、ρp為梁的密度,d31為壓電常數,ε33為介電常數。

表1 壓電俘能器的系統參數及幾何尺寸

k2q+k4q3=0
(11)
當k2>0時,壓電梁不屈曲,系統僅一個穩定平衡點(0,0); 當k2<0時,壓電梁發生屈曲,此時系統有3個平衡點, 其中1個為不穩定平衡點(0,0),另外兩個為穩定平衡點,即
(12)
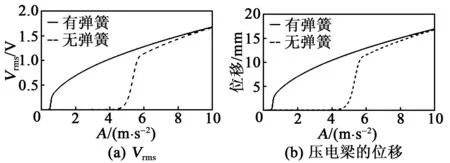
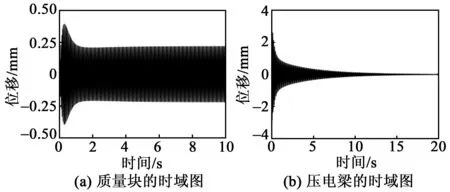
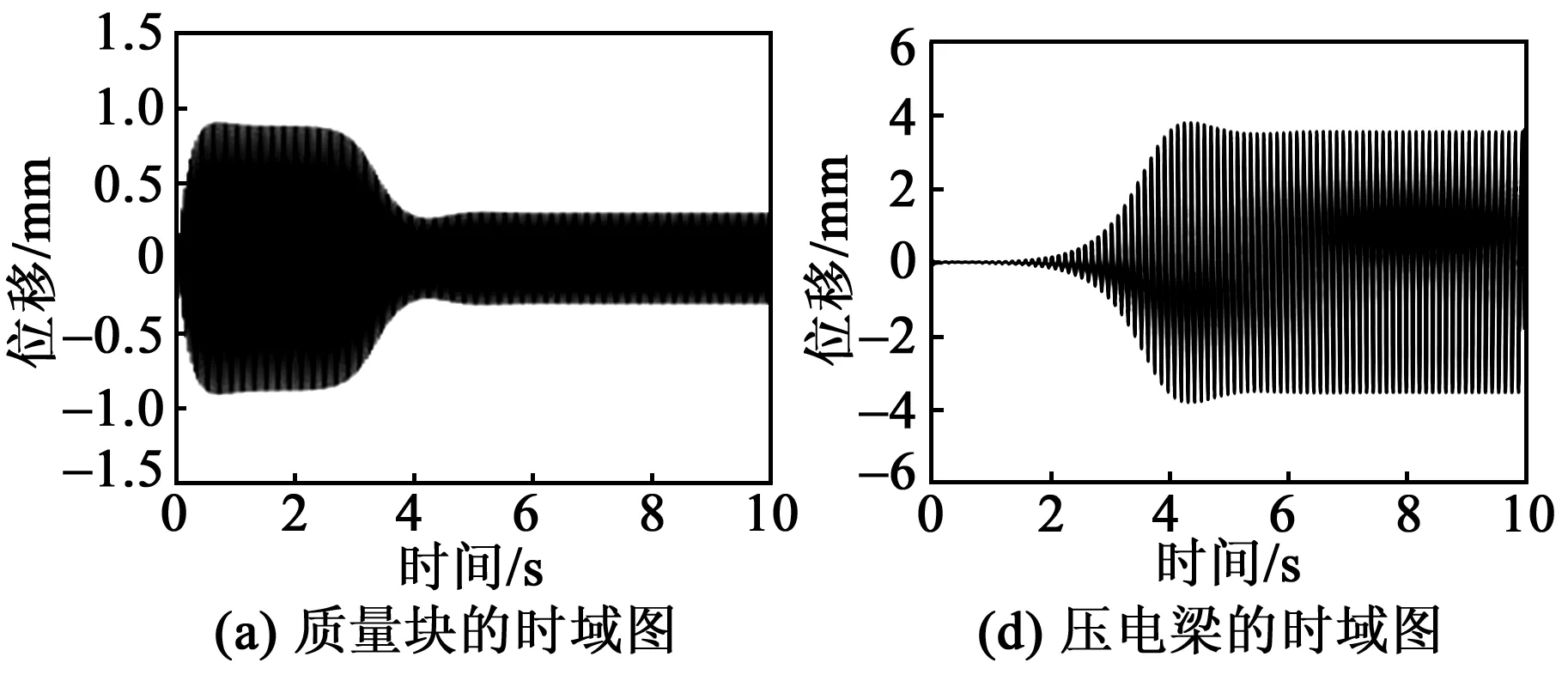
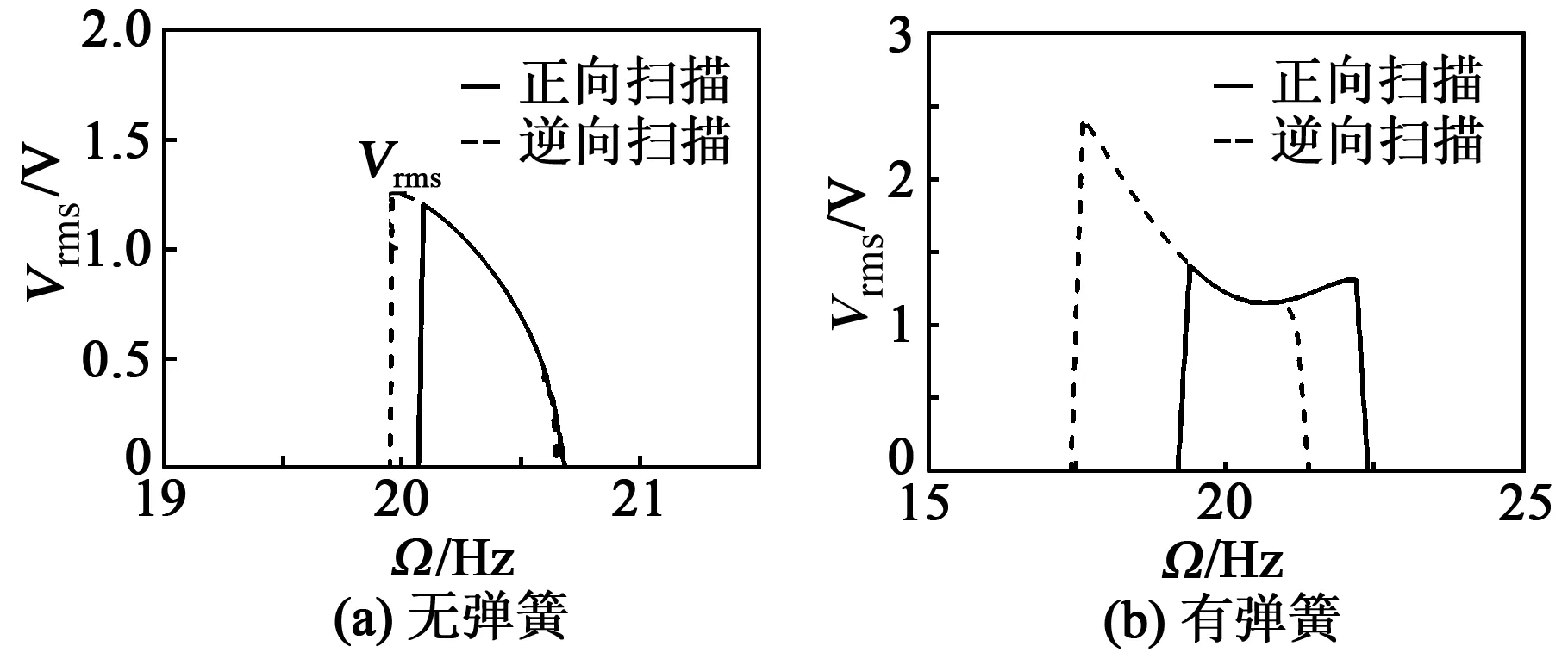
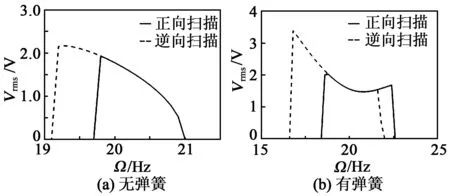
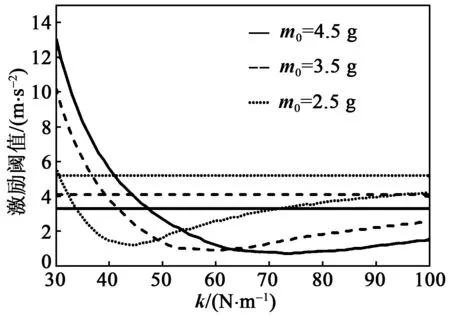
k2=0為壓電梁屈曲與不屈曲的分界點,對應的末端臨界質量用Mc表示。當m0 (13) 當m0>Mc時,壓電梁的固有頻率為 (14) 由表1中的系統參數和幾何尺寸及式(12)~(14)可得到系統的平衡點和壓電梁的f1隨m0的變化規律,如圖2所示。 圖2 壓電梁的平衡點和固有頻率 由圖2可知,Mc≈0.033 kg。當m0 彈簧-質量塊的固有頻率為 (15) 當m0 根據文獻[17],系統的輸出功率與均方根電壓(Vrms)的平方成正比。本文以Vrms作為俘能器的評價指標,則有: (16) 本文主要研究壓電梁在未發生屈曲時的自參數共振系統的俘能性能。根據1.2節的分析,選取m0=0.003 5 kg 本文采用數值分析法進行分析,在未特別說明的情況下,其仿真的初始值均取為0,R取為5 MΩ。 圖3為有、無彈簧時Vrms和壓電梁的位移隨著激勵幅值(A)變化的關系曲線。由圖可知,無論是否有彈簧,該系統都存在一個激勵閾值,只有A大于激勵閾值時,壓電梁才會發生參數共振。有彈簧時激勵閾值為0.5 m/s2,無彈簧時激勵閾值為4.2 m/s2。由此可知,在質量塊與壓電梁之間加裝彈簧能夠大幅降低俘能器的激勵閾值。 圖3 Vrms和位移隨A變化的關系曲線 為了進一步分析質量塊-彈簧的直接共振與梁的參數共振,取A=0.3 m/s2<0.5 m/s2,梁的初始位移取5 mm,作出質量塊和壓電梁時域圖,如圖4所示。 圖4 A=0.3 m/s2時壓電俘能器的時域圖 由圖4(a)可知,彈簧的振幅在1 s內先快速增大,然后又減小到一定值,這是因為彈簧將一部分能量傳遞給了壓電梁。由圖4 (b)可知,梁的振幅經歷了緩慢減小的過程,由于有彈簧的作用,減小的速率較慢。 當A=1.2 m/s2>0.5 m/s2,梁的初始位移為5 mm,作出質量塊和壓電梁時域圖,如圖5所示。 圖5 A=1.2 m/s2時壓電俘能器的時域圖 由圖5可知,質量塊-彈簧發生直接共振,而壓電梁發生了參數共振。質量塊-彈簧與壓電梁之間能量轉換過程為:剛開始激勵時,彈簧首先發生直接共振,經過一段時間后,將能量傳遞給壓電梁,促使壓電梁發生參數共振,再經過一段時間,彈簧的位移減小為一定值。由此可知,壓電梁的參數共振是外部激勵和彈簧共同作用的結果。 當A=5 m/s2時,俘能器的Vrms對于不同Ω的頻率響應如圖6所示。 圖6 A=5 m/s2時壓電俘能器頻率響應 由圖6(a)可知,無彈簧時,俘能器的正、反向掃頻有微小差別,俘能帶寬為20.70 Hz-19.95 Hz =0.75 Hz,均方根電壓峰值為1.2 V。由圖6(b)可知,有彈簧的俘能器的正、反向掃頻差異較明顯,說明加裝彈簧后系統表現出較強的軟化和硬化相結合的特性,增強了參數共振,俘能帶寬為22.4 Hz-17.4 Hz=5 Hz,帶寬提高了6倍以上,均方根電壓峰值為2.4 V,提高了近2倍。 如果進一步增大激勵幅值,差別會更明顯,圖7為A=8 m/s2時壓電俘能器頻率響應。此時,俘能帶寬從5 Hz增加到6 Hz,均方根電壓峰值從2.4 V 增加到3.4 V。 圖7 A=8 m/s2時壓電俘能器頻率響應 圖8為在不同m0下,俘能器的激勵閾值隨k的變化曲線,圖中水平線為未加彈簧時的激勵閾值。 圖8 激勵閾值變化曲線 由圖8可知,隨著k的增大,激勵閾值先減小后增大,呈下凹的變化趨勢。對于不同的m0,當k大于某一特定值,有彈簧時俘能器的激勵閾值均小于無彈簧時俘能器的激勵閾值,這說明只要加裝彈簧的k大于某一特定值,便具有減小俘能器激勵閾值的效能。 在f1∶f2=1∶2時,有彈簧的俘能器出現最小激勵閾值,這說明只有在系統出現了自參數共振時,俘能器的激勵閾值達到最小。 由圖2(b)可知,當m0 將滿足f1∶f2=1∶2的彈簧剛度k稱為最佳剛度K,得到的m0和K間的關系如圖9所示。圖中,當m0=Mc時,f1=0,則K=0。 圖9 m0與K關系曲線 圖10為取最佳剛度時,質量塊-彈簧俘能器的最小激勵閾值隨m0變化的曲線。由圖可知,m0越大,最小激勵閾值就越小,當m0>0.03 kg時,最小激勵閾值接近0。 圖10 m0與激勵閾值關系曲線 圖11為A=5 m/s2,取不同m0及其對應的最佳彈簧剛度時,質量塊-彈簧俘能器的頻率響應圖。由圖可知,m0越大,俘能帶寬就越大,且Vrms也增大。由于隨著m0的增加,f1減小,則圖11中的參數共振頻率隨著m0的增大逐漸向左偏移。 圖11 不同質量下梁的頻率響應 本文提出了質量塊-彈簧參數共振壓電俘能器的結構,利用加裝在質量塊與壓電梁間的線性彈簧,實現系統的自參數共振。 利用擴展哈密頓原理得到俘能器的機電耦合方程。數值仿真結果表明,加裝的彈簧剛度大于某一特定值,便可以減小俘能器激勵閾值,而此特定值與末端質量塊的質量相關。當質量塊-彈簧的固有頻率為壓電梁固有頻率的2倍時,系統可發生自參數共振,此時俘能器的激勵閾值達到最小,同時俘能帶寬也得到擴展。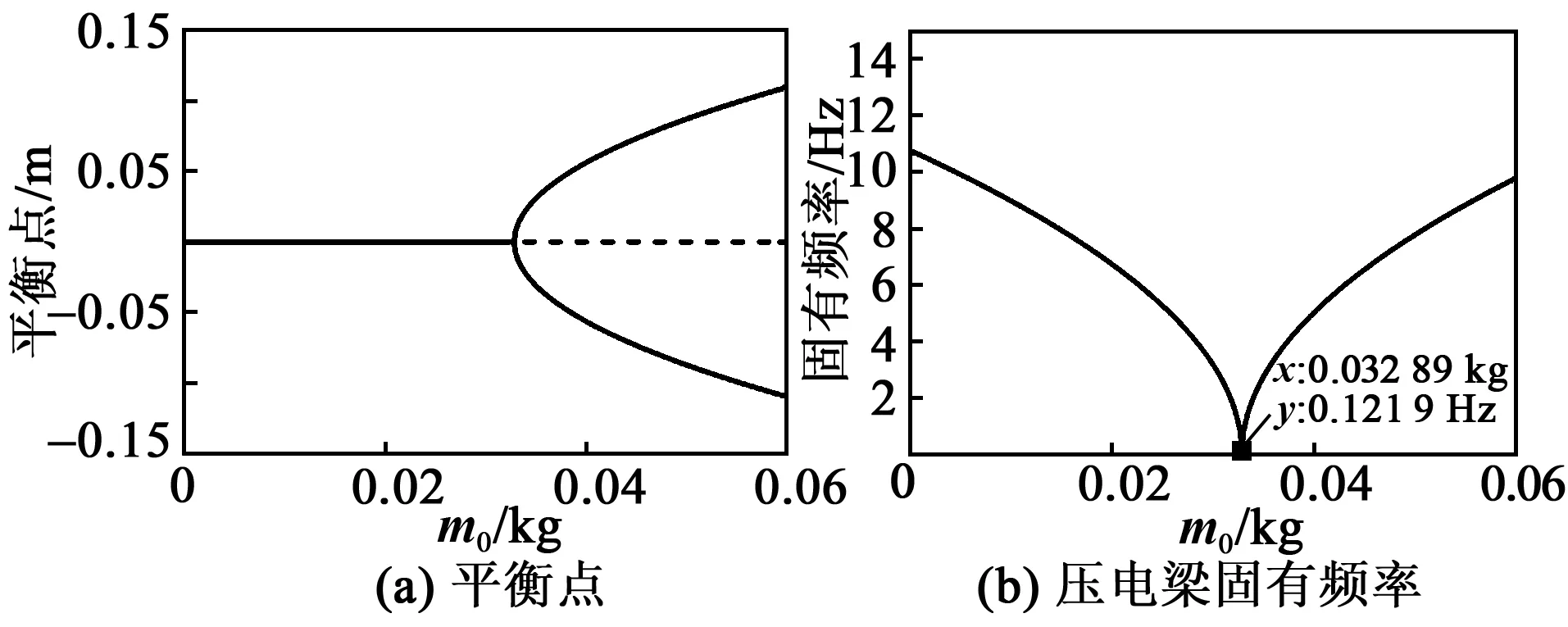
2 質量塊-彈簧壓電俘能器俘能特性分析
3 系統參數對俘能器的運動及俘能特性影響
3.1 m0及k對激勵閾值的影響
3.2 m0與最佳剛度(K)
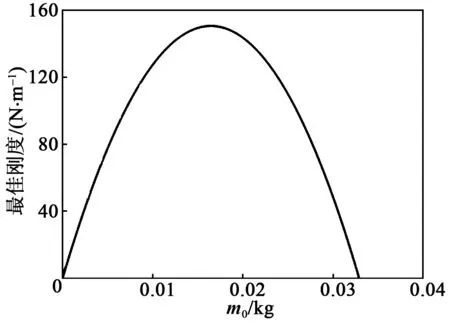
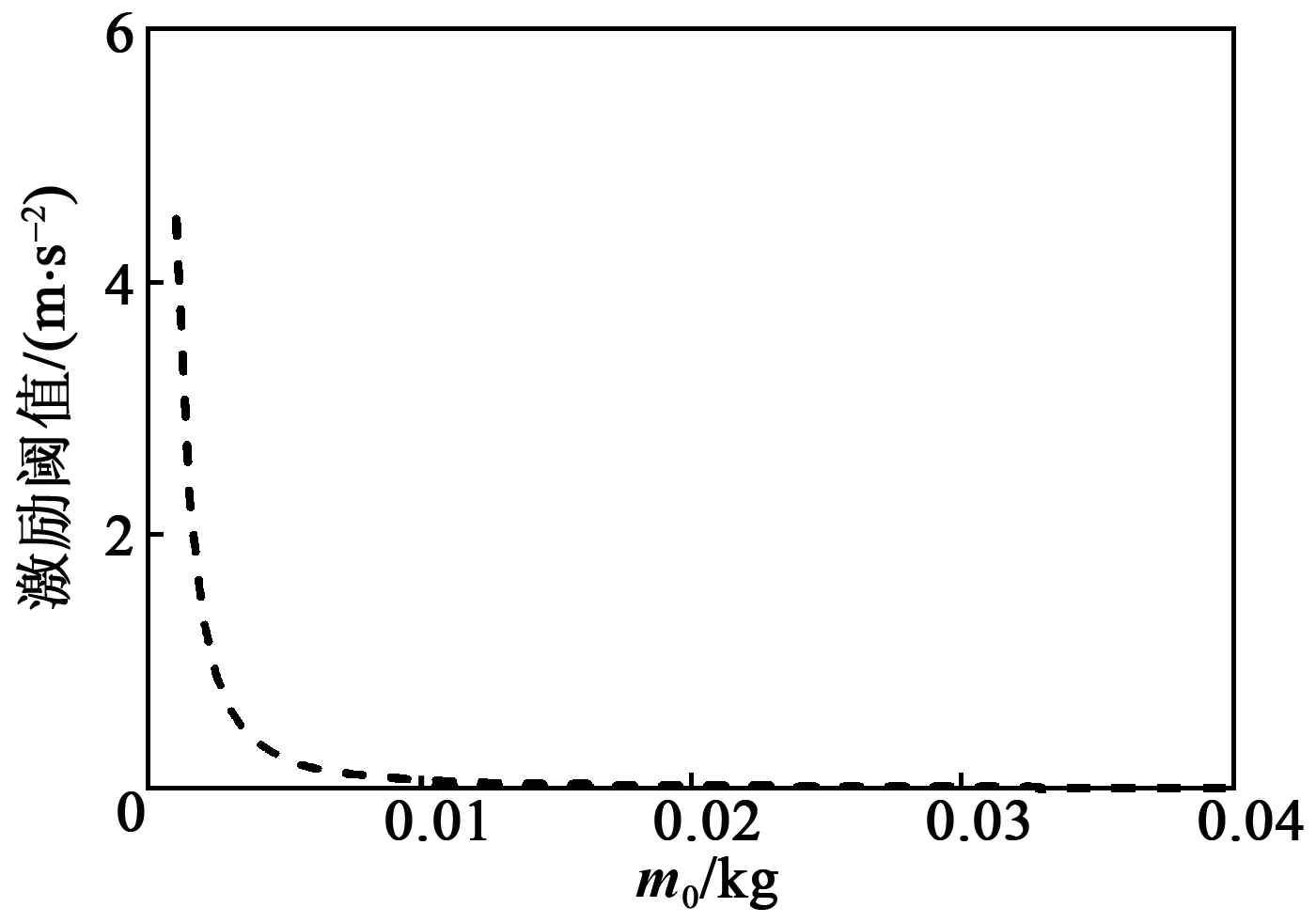
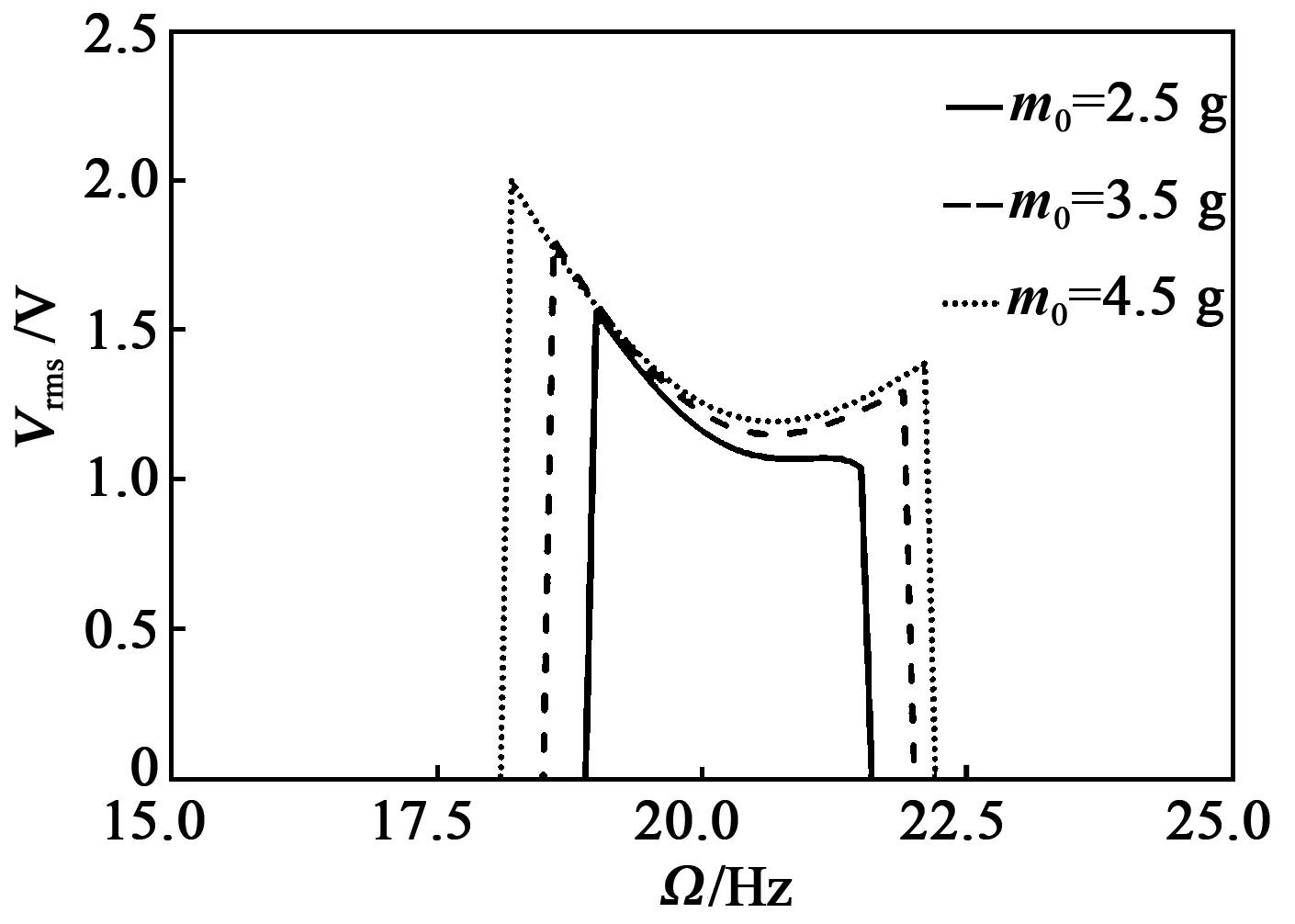
4 結束語

