雙體船湍流脈動壓力激勵水下輻射噪聲預報研究
龔 丞,李 聰,趙 超,王 偉
(中國船舶及海洋工程設計研究院,上海200011)
0 引 言
當船舶航行時,物面湍流邊界層內的速度擾動產生隨機的脈動壓力。這種隨機脈動壓力一方面直接產生輻射噪聲,另一方面激勵物面彈性結構振動并產生輻射噪聲。在低馬赫數情況下,船舶的水動力噪聲主要由脈動壓力激勵船體產生的輻射噪聲構成。目前國內外對流激噪聲的研究都進行了一定程度的簡化。Davies[1]針對矩形平板,采用頻率—波數譜概念,求解彈性結構受湍流脈動壓力激勵的振動和聲輻射。彭臨慧等[2]通過分析湍流脈動壓力頻率譜特性,總結了回轉體受湍流脈動壓力激勵頻譜分布經驗公式。呂世金等[3]運用功率譜的概念和模態平均法計算子單元受湍流脈動壓力激勵產生的聲輻射,建立了航行體水動力噪聲的計算方法。近年來,隨著計算機技術的迅速發展,使得運用計算流體力學(CFD)以及聲學有限元(FEM)方法對實船進行湍流脈動壓力的數值模擬以及水下輻射噪聲的預報逐漸成為可能。張楠等[4]使用大渦模擬的方法對SUBOFF潛艇模型進行了表面脈動壓力的分析,結果表明大渦模擬的計算精度是可靠的。張曉龍等[5]針對平板壁面湍流脈動壓力及其波數-頻率譜進行了數值計算,并探討了湍流脈動壓力的變化規律。江文成[6]利用大渦模擬求解了潛艇的繞流場,將流場計算得到的脈動壓力作為外載荷施加于潛艇結構,研究了流固耦合作用下潛艇的流激噪聲。
本文基于某小水線面雙體船,首先針對縮比模型進行CFD數值模擬,利用大渦模擬技術得到其結構表面的湍流脈動壓力分布,并與試驗數據進行對比,驗證該方法的可靠性。在此基礎上,對實船湍流脈動壓力分布進行模擬,并將脈動壓力頻譜作為輸入,采用聲學有限元方法預報了雙體船的水下輻射噪聲。
1 數值計算方法
1.1 大渦模擬控制方程

濾波后的連續性方程和NS方程可以表示為:
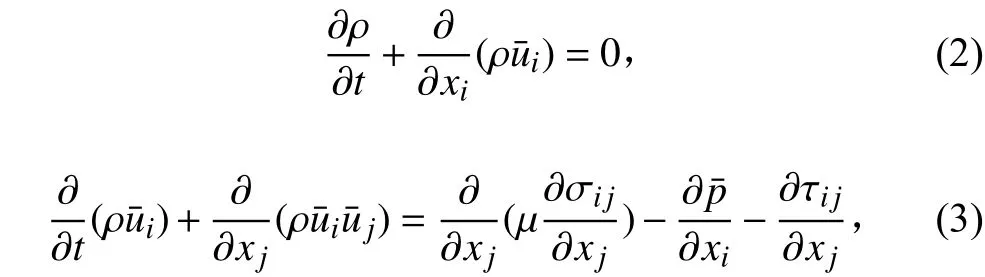
通過對無量綱的連續性方程與NS方程進行網格濾波可以得到濾波后的運動方程:
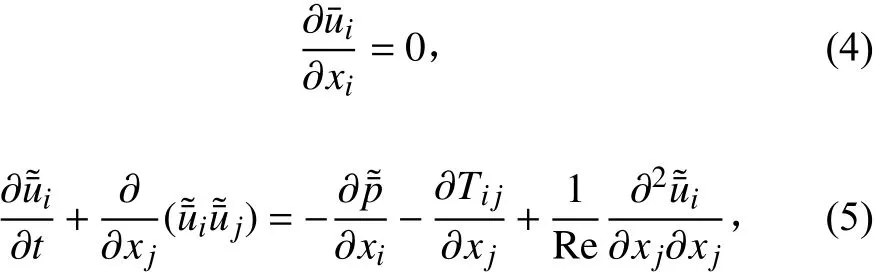
其中亞格子尺度應力為:

1.2 聲學有限元法
采用有限元方法首先將輻射聲場進行離散,假設觀測區域內有n個節點,任意一點的聲場聲壓可近似表示為:
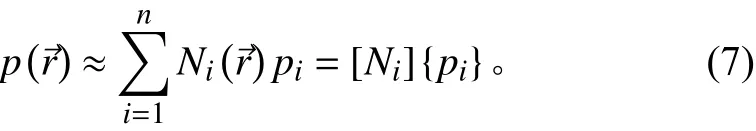
對于一個有限區域內的流體聲場,任意節點i上的聲壓滿足如下方程:
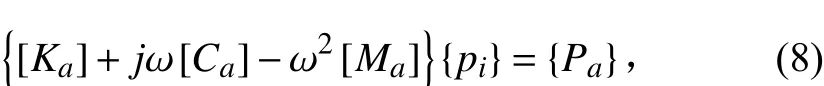
結構受激振動聲輻射動力學方程可以寫作:
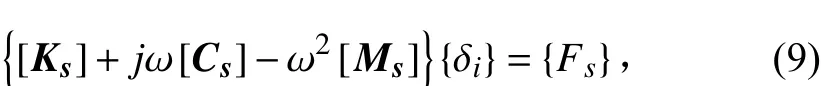
將結構有限元方程和流體聲學有限元方程結合,得到流固耦合有限元方程:

2 湍流脈動壓力的數值模擬
2.1 試驗與數值模型
雙體船湍流脈動壓力試驗在低速風洞中進行,模型長 4.5m,寬 0.36m,高 0.45m,縮尺比為 1:20。試驗中總共沿船長及型深范圍設置了20個測點,其位置如圖1所示。
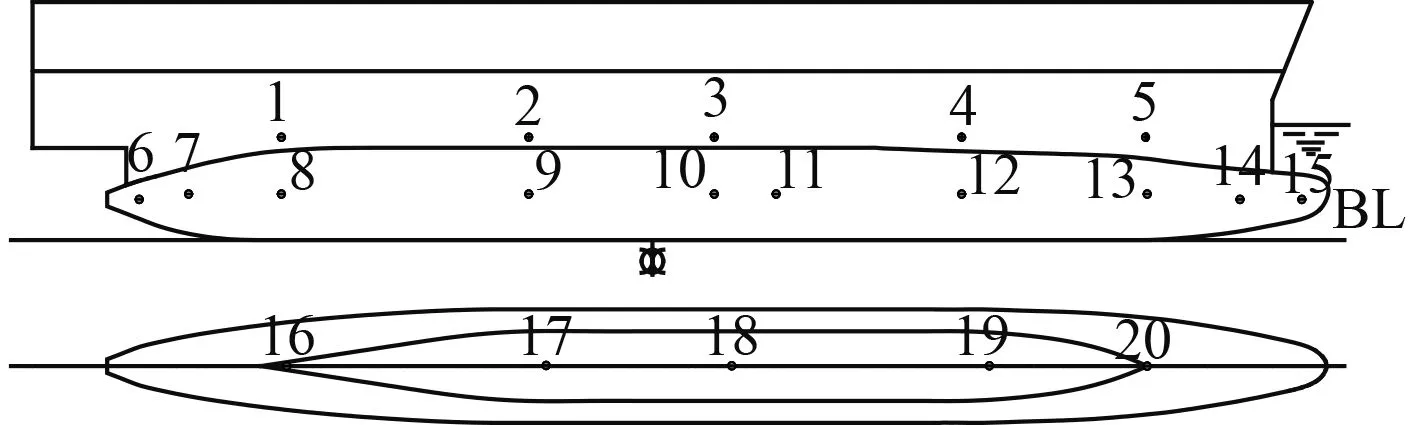
圖1 測點布置Fig.1 Measuring-point arrangement
數值模擬計算區域取為從船首向前1倍船長至船尾向后2倍船長的范圍,網格劃分示意圖如圖2所示。模型網格總數為415萬,實船網格總數為1127萬。
計算域前方邊界條件設定為速度入口,后方為壓力出口;中縱剖面處為對稱邊界條件;船體為壁面邊界條件。為消除流體在邊界上產生的虛假聲波對于近場流體真實脈動的影響[7],在入口邊界與側面邊界施加Bogey輻射條件,并在計算域下游設置了消聲區。時間步長湍流模式采用大渦模擬(LES)方法,時間項采用二階隱式格式離散,動量方程采用限界中心差分格式離散,壓力速度耦合采用SIMPLE算法。計算實船表面脈動壓力時自由面采用了 VOF(Volume of Fluid)方法進行模擬。

圖2 雙體船計算與網格劃分Fig.2 Computational domain and meshing of the catamaran
2.2 數值計算結果
2.2.1 模型脈動壓力計算與驗證
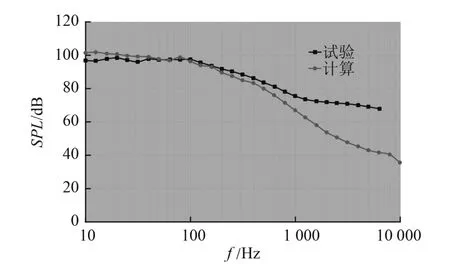
圖3 P1 點脈動壓力計算與試驗對比Fig.3 Comparison between simulation and experiment of turbulent pressure fluctuations at point P1
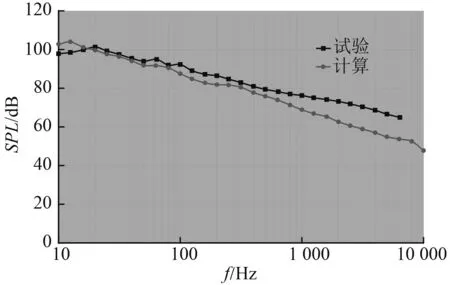
圖4 P5 點脈動壓力計算與試驗對比Fig.4 Comparison between simulation and experiment of turbulent pressure fluctuations at point P5
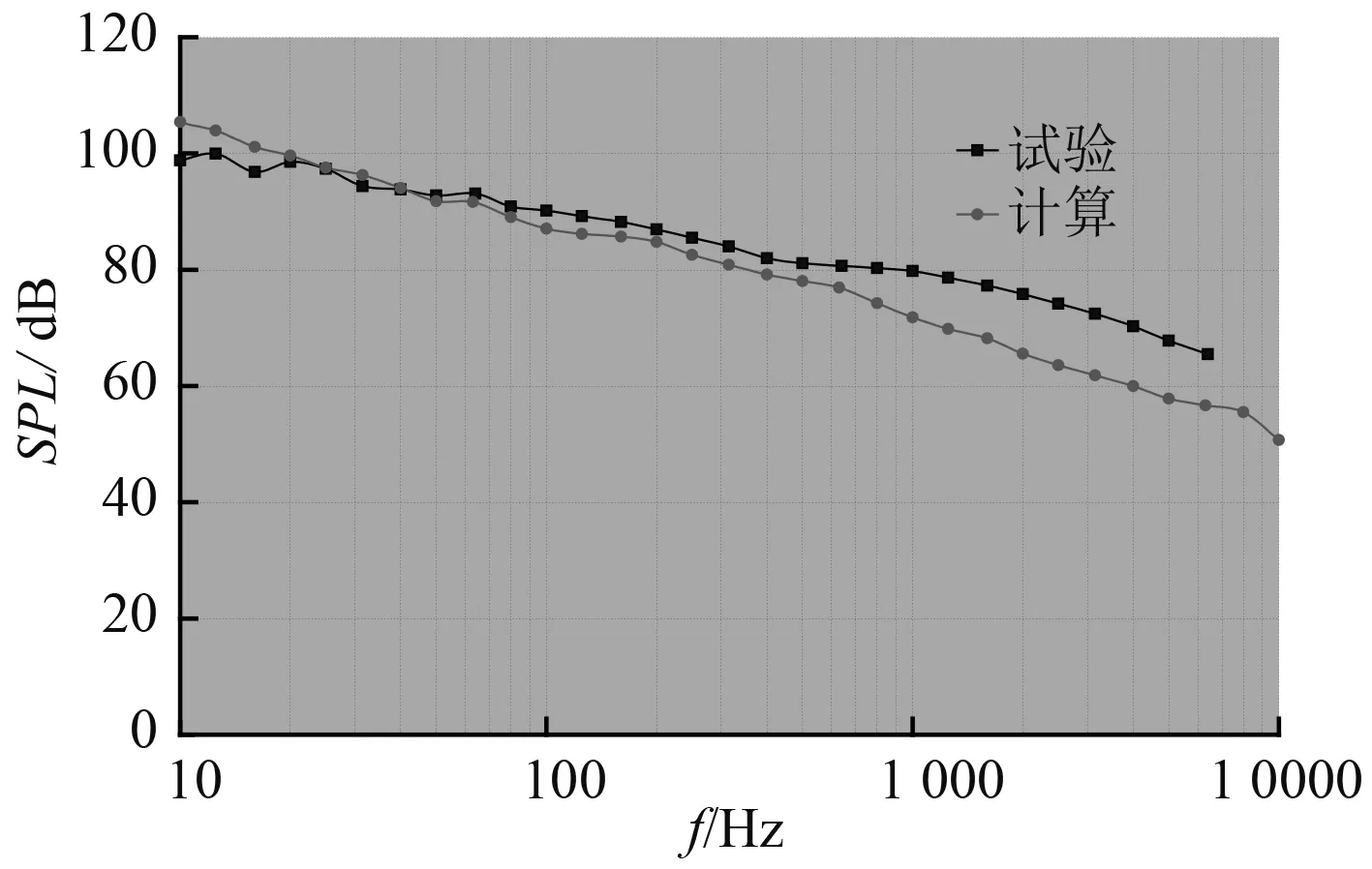
圖5 P10 點脈動壓力計算與試驗對比Fig.5 Comparison between simulation and experiment of turbulent pressure fluctuations at point P10
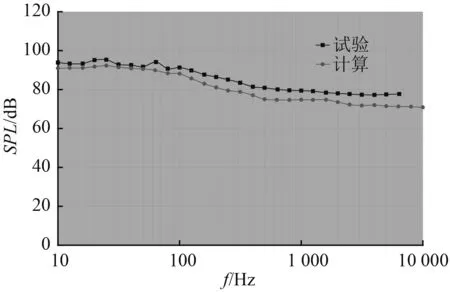
圖6 P19 點脈動壓力計算與試驗對比Fig.6 Comparison between simulation and experiment of turbulent pressure fluctuations at point P19
從模型脈動壓力頻譜計算與試驗對比圖可知:計算得到的脈動壓力功率譜譜型與試驗吻合良好;在2500Hz以下頻段,計算誤差為 1~5dB;在 2500Hz以上頻段,計算誤差為3~7dB。由此可知上述計算方法是可靠的。
2.2.2 實船脈動壓力計算
以6km航速為例,實船流場計算結果如圖7和圖8所示。從實船流線和壓力分布的計算結果可以看出,雙體船2個片體周圍的流場并沒有出現相互干擾的情況。對于片體而言,在自由面附近的流動出現些微波動,遠離自由面位置上的流動則相對光順。
實船脈動壓力頻譜計算結果如圖9所示,脈動壓力計算結果用1/3倍頻程(1/3oct)形式表達。從計算結果看,不同位置的脈動壓力自譜頻響曲線變化趨勢接近,整體趨勢都是低頻幅值較高,到了中高頻幅值開始衰減,與以往回轉體的脈動壓力自譜變化趨勢一致。

圖7 實船表面流線分布Fig.7 Streamline distribution of full scale ship

圖8 實船水下部分壓力分布Fig.8 Pressure distribution of underwater part of full scale ship
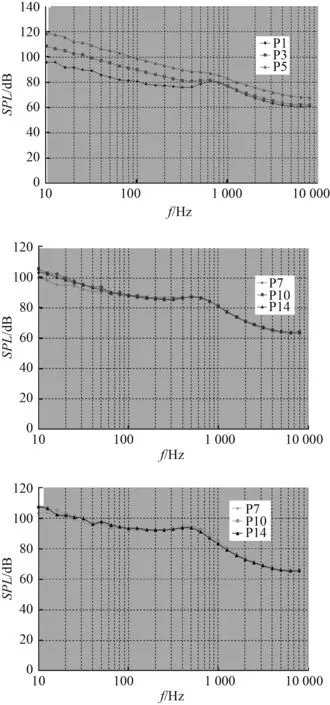
圖9 實船各測點脈動壓力(1/3oct)Fig.9 Turbulent pressure fluctuations of full scale ship at different points(1/3oct)
3 船體水下輻射噪聲預報
通過2.2節中CFD仿真得到了雙體船水線以下表面脈動壓力頻譜,將其作為激勵加載到結構表面,利用聲學有限元法計算船體的水下輻射噪聲。由于實船船體結構尺寸較大,網格數量較多,采用常規的有限元流固耦合建模方法將會帶來巨大的計算量,因此在計算過程中采用自動匹配層(AML)技術,該方法可以大大降低聲學網格量,而且對聲學邊界的形狀沒有要求,從而可以大大提升計算速度。
為了驗證聲學有限元法的可靠性,以幾何形狀簡單的平板為算例進行計算。Heatwole C.M 等[8–9]曾對簡支板的流激噪聲進行過仿真計算和試驗研究,圖10為文獻[8–9]中的試驗值及本文仿真計算結果。從圖中可見仿真計算結果與試驗結果吻合良好,從而驗證了本文數值計算方法對板殼流激噪聲的適用性和準確性。
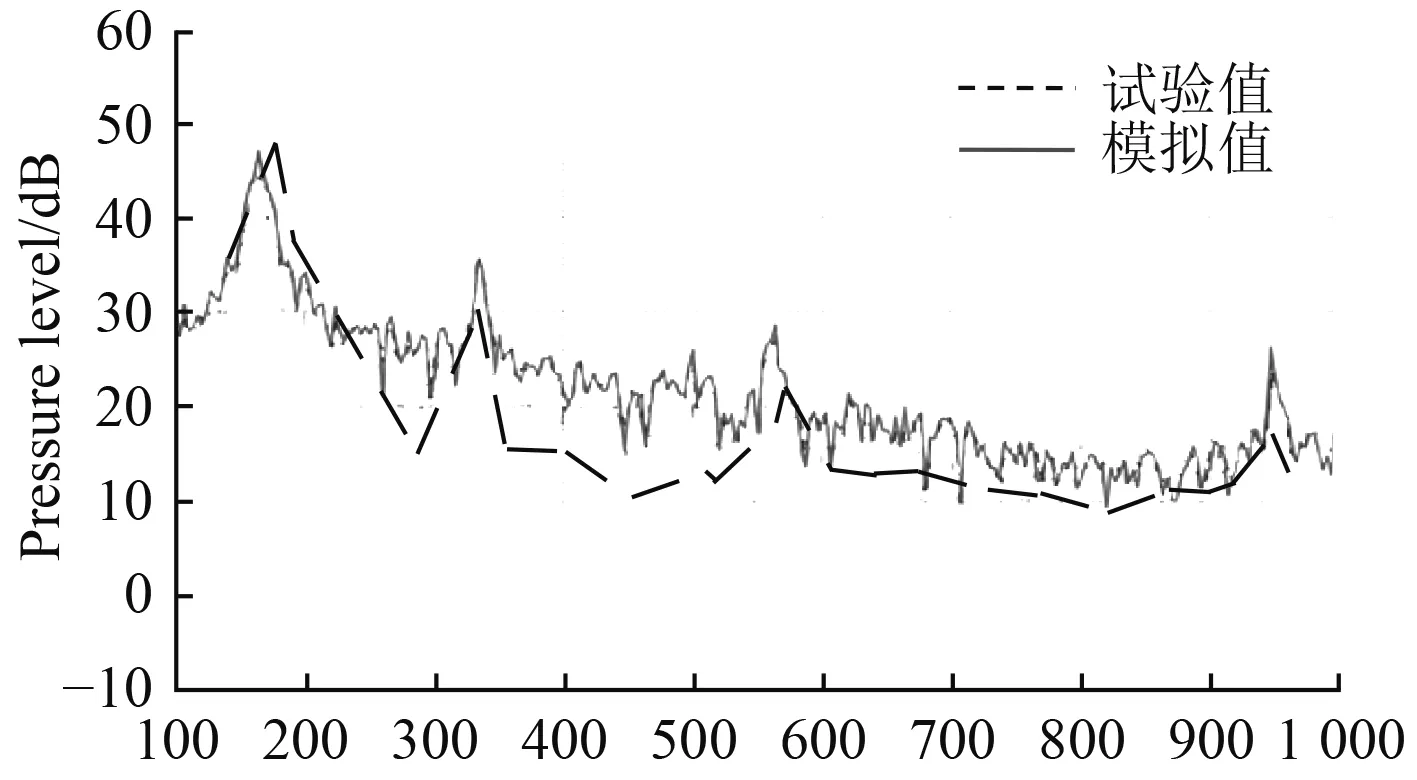
圖10 試驗及仿真計算結果Fig.10 Comparison between simulation and experiment result
雙體船聲學有限元模型及振動測點的位置如圖11~圖13所示。結構部分包含139214個單元,其中梁單元39028個,三角形殼單元4773個,四邊形殼單元 95413 個,流體部分包含 9508256 個體單元,計算頻率取為 20~150Hz。
圖14和圖15為6kn航速下船體表面不同位置的法向振速譜級。從圖中可以看出,不同測點處的振速隨頻率變化規律較為接近,在20~60Hz的范圍內振速譜級幅值隨著頻率增加而降低,在高于60Hz以后,振速譜級幅值趨于平穩。

圖11 雙體船水下結構有限元模型Fig.11 FEM model of the catamaran’s underwater structure

圖12 外場流體區域有限元模型Fig.12 FEM model of fluid region

圖13 振動測點位置Fig.13 Positions of vibration measuring-points
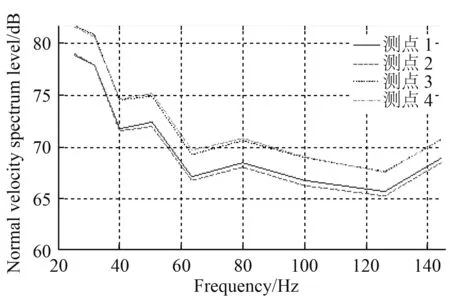
圖14 支柱測點法向振速譜級(1/3oct)Fig.14 Normal vibration velocity spectrum level of measuring-points on pillar area
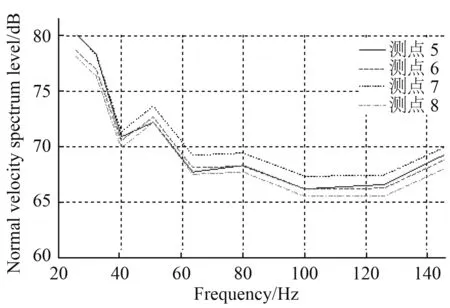
圖15 潛體測點法向振速譜級(1/3oct)Fig.15 Normal vibration velocity spectrum level of measuring-points on submersible area

圖16 有限元法與統計能量法計算結果對比Fig.16 Comparison between results from FEM and SEA method
圖16 為采用聲學有限元方法(FEM)與文獻[3]所采用的統計能量法(SEA)計算得到的雙體船在6kn航速下距離船體1m處的輻射噪聲結果。從圖中可以看出,在低頻范圍內有限元計算結果要高于統計能量法的計算結果,而在高頻段范圍內兩種方法的計算結果趨勢逐漸一致。這可以歸因于統計能量法在低頻段模態密度不夠,統計能量法計算聲輻射本身存在一定的誤差,而采用聲學有限元法則不存在該問題,因此采用有限元(FEA)法計算雙體船聲輻射是較為合理的。
4 結 語
本文采用大渦模擬技術,通過數值模擬計算得到了小水線面雙體船水下部分結構表面的湍流脈動壓力分布情況,并以此為激勵源,利用聲學有限元方法計算得到了雙體船航行狀態下的流激輻射噪聲。經計算發現采用大渦模擬技術能夠有效地模擬航行時船體周圍的湍流脈動壓力分布,較為準確地得到船體湍流脈動壓力。同時,聲學有限元法可以克服統計能量法在低頻段模態密度不足的缺點。計算結果表明,其在低頻段水下輻射噪聲的計算結果高于統計能量法,隨著頻率的提高二者的計算結果逐漸趨于一致,因此能夠較好地預報雙體船的流激輻射噪聲。

