基于歐拉梁的管路吸振器振動特性研究
姚伍平,彭 旭,唐文兵,張針粒,魯民月
(武漢第二船舶設計研究所,湖北 武漢, 430064)
0 引 言
在艦船上,由于轉子不平衡等原因,泵類旋轉機械存在軸頻、葉頻等十分突出的低頻振動線譜,通過基座、管路等通道向外傳遞[1?2]。動力吸振器(DVA)是被動控制振動線譜的有效手段,已經在汽車、船舶、建筑等領域廣泛應用。在設計和應用動力吸振器時,往往將控制對象簡化為質點或多自由度系統,根據等效質量和剛度來確定吸振頻率。艦船管路系統跨徑比大、自身固有頻率低、邊界條件復雜,對吸振頻率和控制效果有較大影響,在開展管路系統吸振設計時,管路已不適合簡化為質點或多自由度系統。因此,有必要針對艦船管路系統的特點,開展管路吸振器的振動特性研究。
吳崇建等[3]用彎曲波法建立了多點支撐歐拉梁的運動方程,研究了用動力吸振器抑制梁共振的特性。Park等[4]建立了懸臂梁上集中質量塊的頻率方程,與前人的研究成果吻合較好。尹志勇[5]等根據梁的能量傳遞理論設計了三向管路動力吸振器,并在試驗臺架上驗證了控制效果。梁建等[6]以附加阻尼吸振器的固支梁作為分析模型,定性研究阻尼吸振器對電路板共振響應的抑制作用,分析了等效質量比、固有頻率比和損失因子等對吸振器控制效果的影響規律。劉天彥等[7]針對管路系統設計了動力吸振器,并通過臺架試驗驗證了吸振器對特征頻率的抑制效果。雖然上述學者針對管路吸振器已開展了一些理論和試驗研究,但是在建模、設計時均未考慮支撐剛度、激勵及吸振器的相對位置等因素對吸振效果的影響。艦船上空間有限,管路支撐方式多樣,研究如何在復雜環境中合理布置管路吸振器,提升控制效果,具有重要的工程意義。
本文以歐拉梁振動理論為基礎,建立任意橫向激勵下,不同邊界下管路—吸振器系統的橫向振動模型,用有限元方法驗證模型的準確性,研究了吸振器安裝部位、控制對象和支撐剛度等對控制效果的影響規律。
1 管路吸振器系統振動模型
1.1 管路—吸振器系統振動模型
在兩端彈性支撐的管路上加裝管路吸振器,當管路長度遠大于管徑時,管路可簡化為歐拉-伯努利梁,吸振器可簡化為質量-彈簧系統。在任意橫向激勵作用下,管路—吸振器的振動模型如圖1所示。
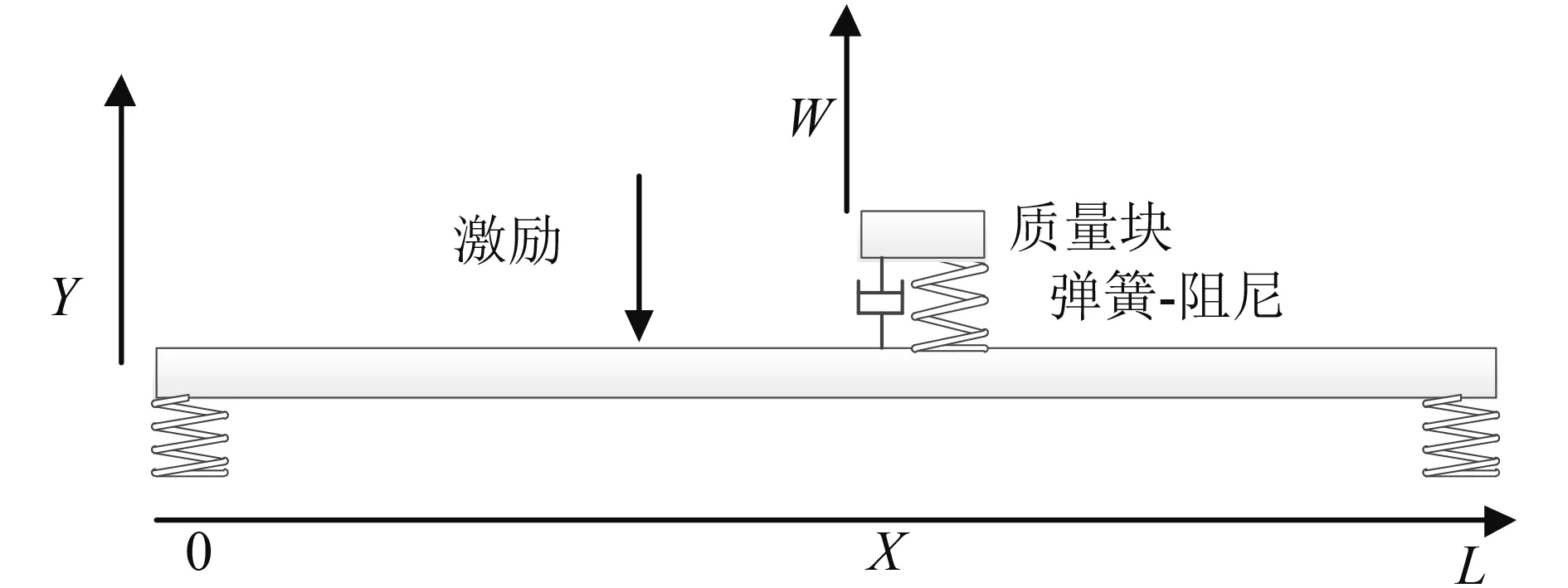
圖1 管路—吸振器振動模型Fig. 1 Pipe-DVA vibration model
管路—吸振器的彎曲運動方程如下:
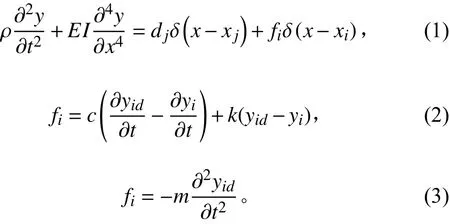
根據振動理論[8],梁的撓度可用振型函數和廣義坐標表示:


將式(4)代入式(1),然后代入式(5),可得:

式中,右邊第1項為激勵源,第2項為彈簧質量系統作用在梁上的力。兩邊分別乘以,在[0,L]上積分,利用振型函數的正交性和歸一性,可得:
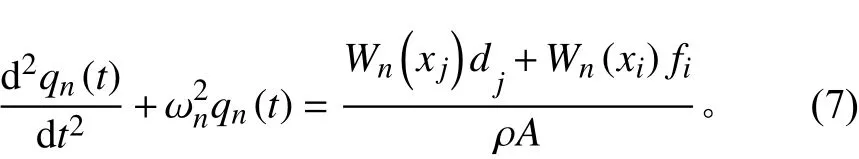
對式(7)進行傅里葉變換,可得:
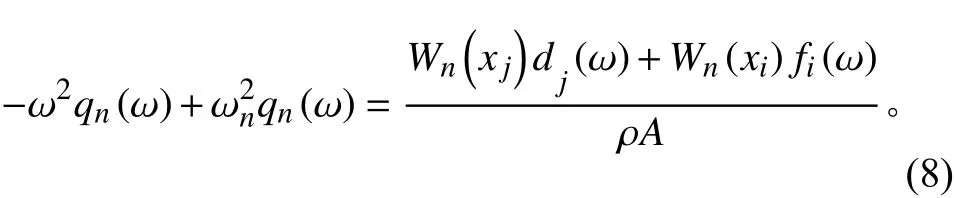
即

與此同時,對式(2)~式(4)進行傅里葉變換,可得:
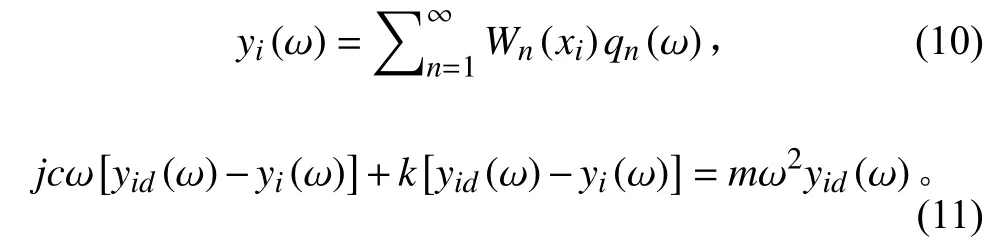

其中:
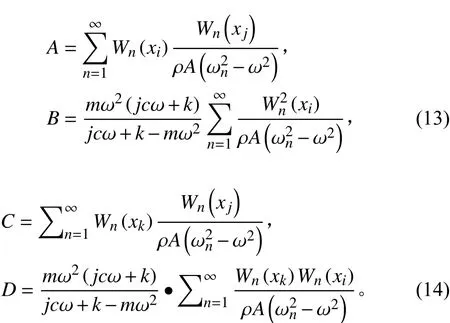
1.2 彈性支撐邊界下歐拉梁的振動方程
方程(5)解的形式為:


式(14)~式(17)若有非零解,則系數的行列式應為0。經過計算,可得:

式(18)即為管路兩端均在彈性支撐狀態下,梁的振動頻率方程。其中,分別為管路兩端支撐的彈性影響因素。
2 計算模型數值驗證
選取一種艦船常用的管路,用有限元方法驗證本文提出計算方法的準確性。管路規格為外徑D=57 mm,內徑d=50 mm,長度L=2 000 mm,材料為鋼材,彈性模量為2.1E11Pa,密度為7 850 kg/m3,泊松比為0.3。用有限元軟件和本文提出的模型,分別計算管路兩端分別為剛性支撐、自由和彈性支撐時,管路的前4階固有頻率和振型圖。在有限元建模時,管路采用的beam4單元,用combin14模擬彈性支撐邊界條件。3種邊界條件下,管路的固有頻率計算結果如表1所示。
由表1可知,在剛性支撐、自由和彈性支撐等3種邊界條件下,本模型計算得到的前4階固有頻率計算結果與有限元計算結果差別在1.6%以內。
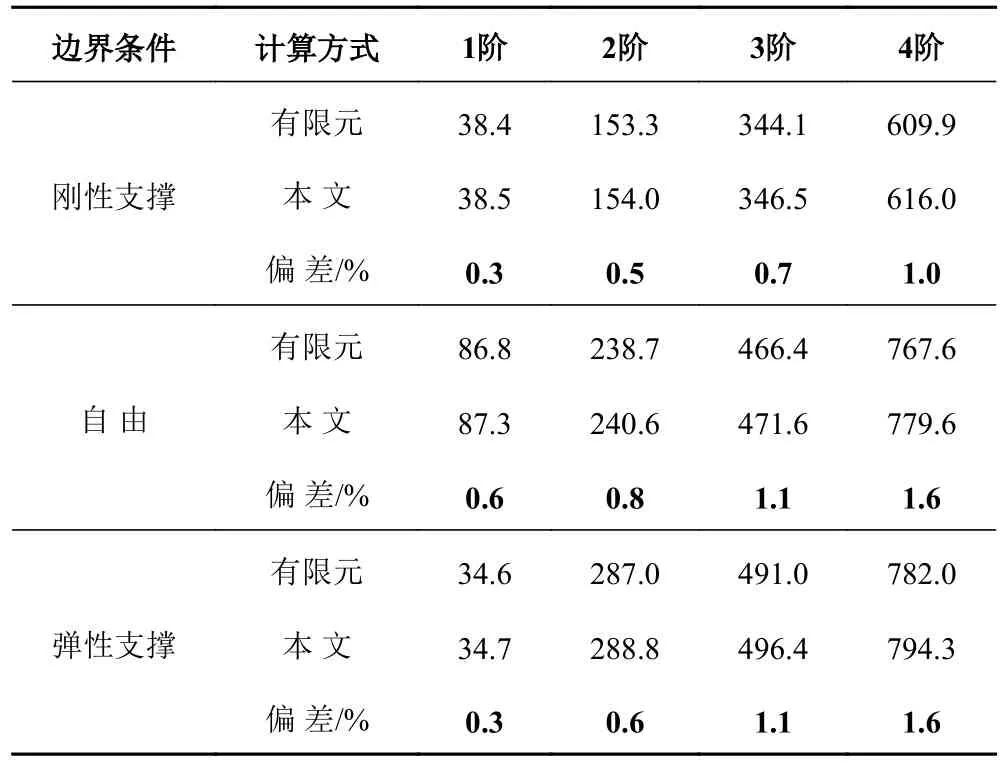
表1 三種不同邊界條件下固有頻率計算結果對比Tab. 1 Comparison of characteristic frequency under 3 boundary conditions
管路兩端分別為剛性支撐、自由和彈性支撐時,用有限元和本文提出的模型計算得到的管路前4階振型圖分別如圖2~圖4所示。
可以看出,在3種邊界條件下,本文計算得到的管路振型圖與有限元計算結果基本一致。綜合固有頻率和振型圖的計算結果來看,本文提出計算模型的準確性得到了驗證。
3 管路吸振器控制效果分析
3.1 管路吸振器參數設計
根據上一節計算結果,可知在上述剛性和彈性支撐邊界下,管路的一階固有頻率分別為為38 Hz和35 Hz,由此可以確定管路吸振器的特征頻率。按照設計經驗,吸振器與管路的質量比初步取為0.02,吸振器的剛度根據吸振頻率及自身質量可確定。圖6為在管路兩端剛性支撐和彈性支撐的邊界條件下,在管路中間x/L=0.5處加裝動力吸振器前后,在安裝部位施加單位激勵后管路的振動響應曲線。
可以看出,在2種邊界條件下,針對特定模態在管路加裝動力吸振器后,在單位激勵下,該階線譜的振動響應得到明顯抑制,而其他頻段基本不受影響。在共振頻率處,不僅在安裝部位,管路整體的振動都得到了有效控制。
3.2 吸振器控制效果影響因素分析
a)吸振器與激勵力位置關系
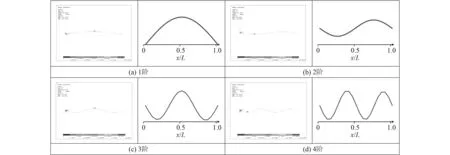
圖2 剛性支撐條件下管路振型圖Fig. 2 Pipe model shape under rigid support
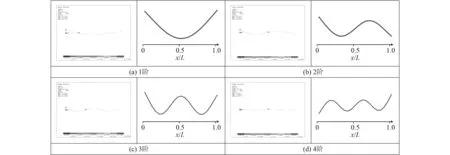
圖3 自由狀態下管路振型圖Fig. 3 Pipe model shape under free boundary

圖4 彈性支撐條件下管路振型圖Fig. 4 Pipe model shape under elastic support
艦船上空間緊張,管路支撐和吸振器的安裝位置都受到一定約束。因此,合理選擇管路吸振器和激勵力的布置位置,對于提高控制效果具有重要意義。圖7為管路吸振器的控制頻率為管路的1階固有頻率(35 Hz),管路分別在剛性和彈性支撐狀態下,受單位激勵作用管路的振動響應。
由圖7可以看出,針對特定管路模態,不論管路兩端為剛性還是彈性支撐,激勵力及吸振器的位置均對管路的振動響應有重要影響。針對控制頻率,激勵越靠近振動模態的位移極值點,管路整體的振動越大;吸振器布置越靠近振動模態的位移極值點,管路整體的控制效果越好;如果管路兩端為剛性支撐邊界,不論吸振器及激勵的位置如何變化,總有較好的控制效果;若管路兩端為彈性支撐,如果激勵的位置不在位移極值點,那么吸振器離激勵位置越遠,控制效果越差。在圖7(a)中,當DVA的位置與激勵距離△=0.75L時,加裝吸振器后管路最大位移與加裝前的比值為0.65,加裝DVA對管路振動控制效果較差。

圖5 中間加裝動力吸振器前后安裝部位振動響應對比(兩端剛性支撐)Fig. 5 Vibration response before and after DVA install(Both ends fixed)
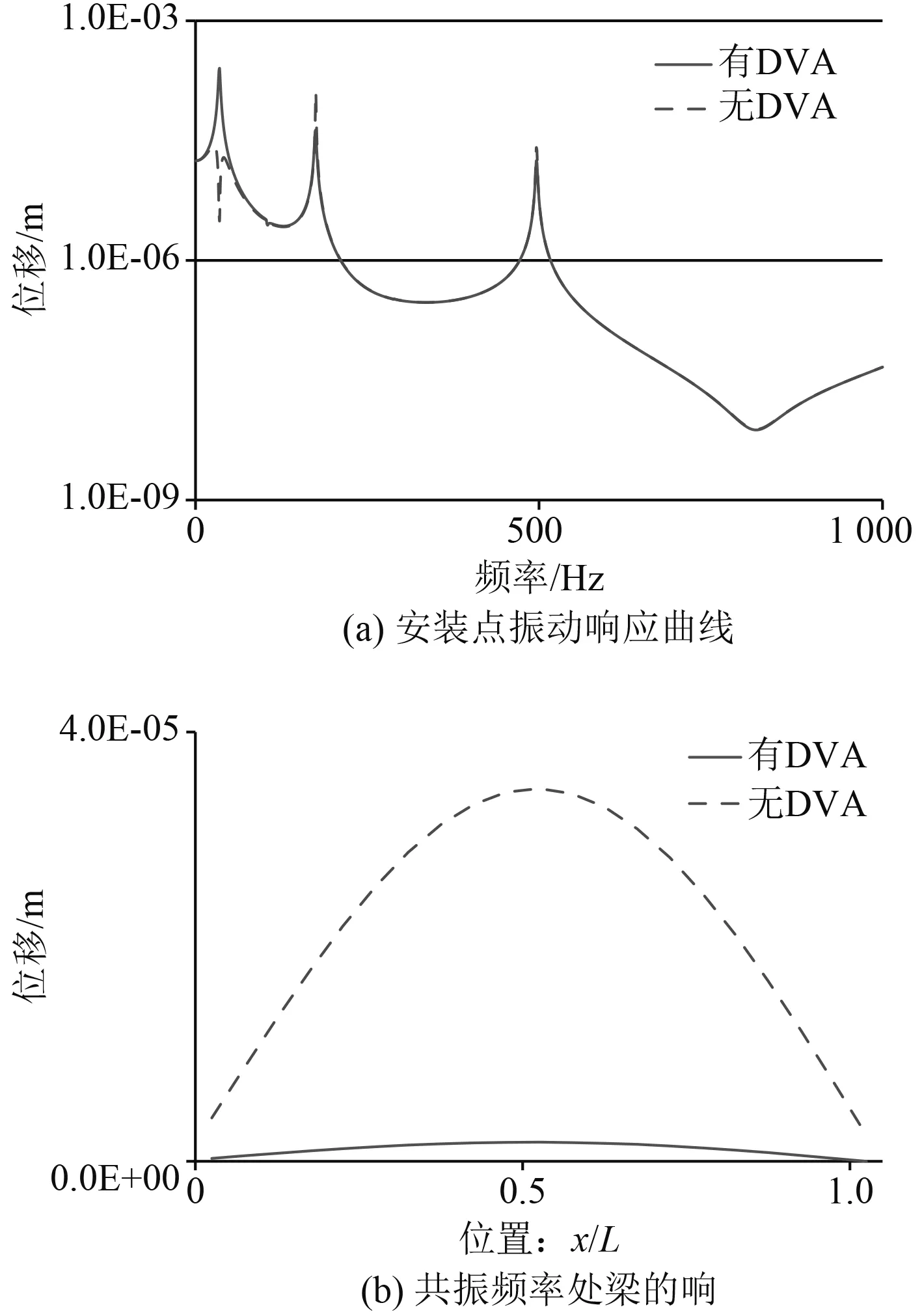
圖6 中間加裝動力吸振器前后安裝部位振動響應對比(兩端彈性支撐)Fig. 6 Vibration response before and after DVA install(Both ends with elastic support)
b)非共振頻率控制效果
艦船上管路系統的振動響應線譜除了來自于系統自身固有頻率,也包含來自設備的軸頻、葉頻等線譜激勵,后者在很多時候是管路振動響應線譜的主要來源。因此,針對線譜激勵的控制具有重要的實際意義。同樣受限于空間,合理選擇吸振器的布置位置,對于控制效果也具有重要意義。以艦船上常見的100 Hz振動激勵為對象,設計控制頻率為100 Hz的吸振器。圖8為管路分別在剛性和彈性支撐狀態下,在100 Hz頻率處,激勵位置與吸振器位置的變化對管路振動響應的影響規律。
由圖8可以看出,針對特定激勵,不論管路兩端為剛性還是彈性支撐,激勵力及吸振器的位置均對管路的振動響應有重要影響。針對控制頻率,如果吸振器的安裝位置與激勵的位置重合,那么管路整體的振動會受到良好抑制,如果激勵和吸振器均處于振動模態的位移極值點,抑振效果更加顯著;如果吸振器的安裝位置與激勵位置不重合,不論管路兩端是剛性還是彈性支撐,隨著二者之間距離的增大,控制效果越來越差;當吸振器與激勵的距離大于一定值時,會產生嚴重的負面效果,顯著放大管路的振動。在圖8(b)和圖8(e)中,激勵的位置處于x/L=0.25,若吸振器的位置加在x/L=0.75處,那么加裝DVA后,管路的振動反而被放大,加裝吸振器后管路上最大位移幅值與加裝前的比值分別為3.22和4.79。
綜上,在針對特定模態頻率和針對特定激勵應用吸振器時,管路系統的振動特性存在較大差異,后者對激勵及吸振器位置更為敏感。因此,以特定激勵為管路系統振動控制對象時,吸振器的布置應盡量靠近激勵位置。
3)管路支撐剛度
由管路的頻率方程可知,管路的振動特性不僅取決于自身,也取決于管路兩端的支撐剛度。綜合而言,管路支撐的彈性影響因素對管路的振動特性影響最大。圖9為2種規格管路的1階固有頻率隨彈性影響因素的變化情況。管路規格分別為D=57 mm,d=50 mm,L=2 000 mm和D=114 mm,d=100 mm,L=3 000 mm。

圖7 激勵及吸振器位置對特定模態控制效果的影響Fig. 7 Influence of DVA position on control effect aimed at specific modal

圖8 激勵及吸振器位置對特定激勵控制效果的影響Fig. 8 Influence of DVA position on control effect aimed at specific excitation
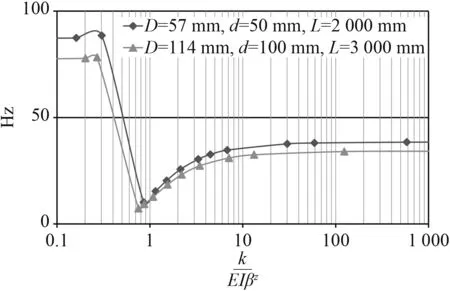
圖9 管路一階固有頻率隨支撐剛度的變化曲線Fig. 9 First characteristic frequency vs support stiffness
4 結 語
通過本文的研究工作,可以得出以下結論:
1)本文提出的一種管路吸振器的振動特性計算方法,在剛性支撐、自由支撐和彈性支撐等不同類型的邊界條件下,管路的前4階固有頻率與有限元計算結果偏差在1.6%以內,振型的計算結果基本一致。
2)針對特定模態頻率,如果激勵的位置不在振動極值點,那么吸振器離激勵位置越遠,控制效果越差,甚至沒有控制效果;吸振器及激勵的位置對管路剛性支撐條件的影響要小于彈性支撐。針對特定頻率的激勵,吸振器與激勵位置重合時有良好的控制效果,如果吸振器的安裝位置與激勵位置不重合,不論管路兩端是剛性還是彈性支撐,那么隨著二者之間距離的增大,控制效果越來越差,在某些條件下管路振動甚至放大超過3倍。因此,在應用管路吸振器時,應區分控制對象為特定模態頻率還是特定激勵;以特定激勵為管路系統振動控制對象時,高度重視吸振器的布置位置,盡力使其靠近激勵。
3)若彈性影響因素特定區間內,管路1階固有頻率對支撐剛度十分敏感。當大于10時,管路兩端類似剛性支撐,支撐剛度的增大對1階固有頻率的影響在10%以內;當小于0.1時,管路兩端類似自由狀態,支撐剛度的減小對1階固有頻率的影響在1%以內。因此,以管路振動模態頻率為控制對象設計吸振器時,需要重視管路兩端支撐剛度的影響。

