q-二項式定理、q-高斯和公式及q-歐拉變換公式的概率證明

湖南環境生物職業技術學院 劉現芳

利用隨機變量的期望值來證明一些重要定理，這種概率方法是數學領域的一個重要手段， 并且在數論、代數、組合數學等數學領域已有比較成熟的研究，而在基本超幾何級數中亦有許多重要應用。例如，在統計學領域里，Kadell[3]將Ramanujan’s1ψ1和實現了一種新的證明方式—概率證明，再比如，Fulman[1]利用Markov Chain 概率理論將Rogers-Remanujan 等式得到概率證明方法；而Chapman[2]在Fulman 的理論成果上加以研究，也用概率的方法推廣證明了Andrews-Gordon 等式。

根據文[4][5]的研究成果容易知道，文章中構造了一個離散型隨機變量X，并且根據隨機變量提出了一個全新的概率分布W（x；q），如下：

滿足：pn，k（x；q）＞0，Σpn，k（x；q）=1，x＜0，0＜q＜1，n=0，1，k=0，1，Λ。

利用上式概率分布，得到了q-二項式定理、q-高斯和公式的一個概率證明方法，并且得到了幾個新的求和公式及變換公式。

隨機變量的期望值是概率統計學中的一個非常重要的理論，如果我們假設存在離散型隨機變量X，若它的概率密度函數為p（x），那么我們將E[X]作為隨機變量X 的期望值的一個標記，其定義如下：

首先是知識準備，我們給出引理1、引理2 以及一些重要的知識概念：

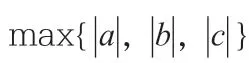
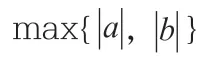
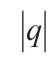
q-升階乘的定義為：

并且，

q-二項式系數我們定義如下：其中任意的n，k ∈N，

q-升階乘的乘積形式定義：

若任意的n，k ∈z+，有：

我們將上式級數rs[6][7]稱為雙邊級數。

當s=r+1 時，Heine 將q-基本超幾何級數r+1r 的定義如下：

如果s=r+1，而且qa1a2…ar+1=b1b2…br，我們稱r+1r 這個基本超幾何級數是平衡的（balanced）。

從Ramanujan’s1ψ1中可以導出一個Andrews-Askey 積分[9]：

其中，分母不含零因子。

最近，文[10]更進一步地推廣了Andrews-Askey 積分，有如下形式：

其中，分母不含零因子。

文章的主要目的是利用給出的期望公式對q-二項式定理、q-高斯和公式進行簡單的概率證明，并且利用引理3 推廣的新q-積分公式證明了q-歐拉變換公式。

一、q-二項式定理

q-二項式定理是數學中的一個重要結論，并且廣泛地應用在特殊函數、物理學、量子代數和量子統計學等科學領域。Cauchy、Heine[11]和Jacobi 就非終止型q-級數導出了q-二項式定理。此外，還包括許多q-二項式定理的證明方法。例如，Askey 利用有限差的方法更好更簡便地給出了證明等。本小節，我們通過隨機變量的期望值的計算，從而得到了q-二項式定理的一個簡便證明方法。

定理1[6][7]q-二項式定理：

證明：在引理1 中，我們令c=0，有：

結合上式及引理2，容易得到：

因此，我們有：

即

將ab 用a 代換，可以得到：

q- 的高斯和公式在q- 級數中占有重要地位。1847 年，Heine[11]導出了q 化的高斯和公式；在組合數學理論基礎上，Stanton 和Joichi 得到了q-高斯和公式的雙射證明方法;Rahman和Suslov 利用一階線性差分方程證明了q-高斯和公式。下面，我們利用概率方法對q-高斯和公式進行簡單的證明。

定理2[6][7]q-高斯和公式：

在引理2 中，我們令a=0，有：

結合(23)和(25)兩式，易得：

將c 用a 代換，b2用c 代換，易得：

由此，我們證明了q-高斯和公式。

注釋1：我們對于q-二項式定理、q-高斯和公式的證明過程比文[5]的證明過程更簡單。

三、q-歐拉變換公式

q-歐拉變換公式是q 級數中的一個重要變換公式。Heine[11]導出了q 化的歐拉變化公式，本節中，我們在利用文[10]推廣的新的積分公式的前提下，給出了q-歐拉變換公式的概率證明。

定理3[6][7]q-歐拉變換公式：

證明：設-1＜x＜0，那么在引理1 的等式（3）中，我們設特殊值a=0，則有：

另一方面，利用定義(12)，我們易得：

利用定義(13)，結合(30)和(31)，有：

根據引理3 的等式（15）和概率分布W（x；q），有：

因此，我們可以得到：

結合(29)和(32)兩式，化簡可得：

在上式中，將（c，cx，bcx）依次用（a，b，c）代換，易得：

由此，我們證明了q-歐拉變換公式。

注釋2：利用Heine 變換公式

進行兩次迭代，我們也可以得到q-歐拉變換公式。

注釋3：上述所有證明過程中，我們都是假設-1＜x＜0。實際上，當-1＜x＜1 的時候，利用解析延拓定理，上述結論仍然成立。

注釋4：我們認為隨機變量X 服從概率分布W（x；q）在q-級數中有更廣泛的應用，利用概率分布，我們可以更進一步地證明q-級數中更多的和公式及變換公式。