積累基本圖形,走入幾何
湖北省武漢市第十二初級中學 裴 紅
一、積累基本圖形的意義
初學幾何的同學總感覺證明題目太難了,苦于看不清圖形,找不到證明的方法,特別是對于初一年級的學生而言,學會識圖是幾何入門的第一關。學會識圖主要指:(1)能從不同角度、不同方位去看圖形;(2)熟悉基本圖形;(3)利用標準圖形認識變式圖形;(4)善于把復雜圖形分解為基本圖形。由此可知,在初一學生學習幾何的過程中,識別基本圖形的過程就是學會識圖的過程。
二、積累基本圖形的途徑
1.課本學習的總結歸納
中學生的解題積累基本上就是課本的學習積累,因此,對課本學習內容進行總結歸類,是積累基本圖形的一個基本途徑。比如:
(1)每一個關鍵概念、每一條重要定理都對應一個基本圖形。相交線(垂線)、平行線是兩條直線的位置關系,是基本圖形;對頂角、鄰補角、“三線八角”,也可以算是基本圖形;三角形的邊、內角、外角、中線、高、角平分線、面積等也組成基本圖形。
(2)每一單元學習之后,對例題、作業進行一些總結,弄清一共有幾個主要基本圖形?每一基本圖形對應哪些基本結論?對于這些基本結論各有哪幾種解決方法?哪種方法比較簡潔?這既是一個解題反思的過程,又是一個積累基本圖形和基本結論的過程。下面舉例說明。
例1:觀察下面兩個八年級上冊的課本原題。
(第17 頁習題9)如圖,∠1=∠2,∠3=∠4,∠A=100°,求x 的值。

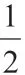
例1 變式1:將基本圖形1 的條件變化,可得基本圖形2 與基本圖形3。
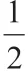
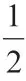
例1 變式2:將基本圖形1 一般化,可得基本圖形4 和基本結論4:如基本圖形4,在四邊形ABPC 中,∠P=∠A+∠ABP+∠ACP。
進一步觀察基本圖形4 可得下列結論:
基本結論5:∠P>∠A。
基本結論6:AB+AC>PB+PC。
2.解題過程的分析提煉
一方面,可以將題目加以組合或分解,使組合后的新問題或分解后的各個子問題成為基本圖形;另一方面,也可以將基本圖形加以深化或重組,用整合過的綜合圖形來解決所面臨的問題。
例2:(節選自七年級下冊課本第7 頁練習2)如圖2-1,∠1 與哪個角是同旁內角?它們分別是哪兩條直線被哪一條直線所截形成的?
例2 的圖形比較復雜,要解決這個問題,就需要確定∠1 是哪兩條直線被哪一條直線所截形成的,所以我們引導學生分類討論截線,得到圖2-2、圖2-3、圖2-4,從而解決問題。
3.基本圖形網絡化
這種積累基本圖形途徑的本質是:形成知識網絡,優化認知結構,在這個積累知識的過程中,會形成越來越清晰的思維路徑圖,而這個思維路徑圖又會在基本圖形積累中越來越牢固、越來越暢通。下面舉例說明:
例3:
(1)“疊加”探究基本圖形
學習了三角形外角定理后,可以得到基本圖形5。將兩個基本圖形5 疊加可以組成基本圖形2 和基本圖形6,再將兩個基本圖形6 疊加又可以組成圖3-2。
(2)“分解”探究基本圖形
如圖3-1,在基本圖形4 中,延長BP 交AC 于M,可以得到兩個基本圖形5。
(3)“互推”探究基本圖形
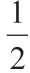
(4)“結網”探究基本圖形
整體觀察上述思維路徑圖,可以發現其核心圖形為基本圖形5,觀察從基本圖形2 到基本圖形1、基本圖形3 的互相轉化的過程,它們主要是依據基本圖形7 構造直角三角形,利用基本圖形5 將這三個結論串聯起來,就可以達到“憶一個出一串”的效果。
隨著學生所學知識的增多,上述思維路徑圖還會不斷生長。幾何學習的過程就是通過不斷完善思維路徑圖,提高學生識圖、辨圖、用圖的空間能力,發展學生的空間觀念。

