考慮應(yīng)變率的廣義壓電熱彈理論及其應(yīng)用1)

李吉偉 何天虎

(蘭州理工大學(xué)理學(xué)院,蘭州 730050)

引言

隨著器件小型化及現(xiàn)代加熱技術(shù)的發(fā)展,如超短激光脈沖,微波等,用于模擬材料在極短時間內(nèi)[1-9]的熱力學(xué)行為的經(jīng)典熱彈性理論令人質(zhì)疑.針對極端條件下的傳熱問題,學(xué)者們對傅里葉定律進行了修正,基于不同機理,得到了形式各異的非傅里葉熱傳導(dǎo)模型.第一個修正的模型是由Cattaneo[10]和Vernotte[11](C-V) 提出的,他們通過弓入熱松弛時間因子和熱流率的乘積項對經(jīng)典傅里葉定律進行了修正,得到了波型的熱傳導(dǎo)方程.此后,Lord 和Shulman(LS)[12]及Green 和Lindsay(G-L)[13]發(fā)展得到了廣義的熱彈性理論.其他的廣義熱彈理論模型包括:考慮或不考慮耗散的G–N[14-16]模型、慣性熵模型[17]、熱質(zhì)模型[18]等.在過去的數(shù)十年間,分?jǐn)?shù)階微積分在描述反常擴散等問題方面得到了長足發(fā)展,并被學(xué)者們弓入了熱彈性理論,建立了分?jǐn)?shù)階型的廣義熱彈性理論,如Povstenko[19]提出的分?jǐn)?shù)階熱彈性理論,Youssef[20]提出的L-S 型分?jǐn)?shù)階理論,Sherief等[21]、Ezzat[22]和于亞軍等[23]的分?jǐn)?shù)階理論,以及G-L 型分?jǐn)?shù)階理論[24]等.許光映等[25]基于分?jǐn)?shù)階理論,研究了非高斯分布激光熱源輻射下半無限大體內(nèi)部的復(fù)雜傳熱過程及熱變形,給出了溫度場和應(yīng)力場的解析解.針對電磁介質(zhì),學(xué)者也建立了廣義電磁熱彈理論來研究相關(guān)問題,如Sherief 和Anwar[26]將第三類熱邊界條件應(yīng)用于圓環(huán)的內(nèi)外表面,研究了無限傳導(dǎo)和有限傳導(dǎo)圓環(huán)的動態(tài)響應(yīng)問題.何天虎等[27]求解了無限長圓柱體的廣義電磁熱彈問題.除此之外,在廣義熱彈問題中,考慮記憶依賴效應(yīng),也弓起了學(xué)者們的關(guān)注.張培等[28]基于記憶依賴非局部廣義熱彈理論,研究了兩段固定、受移動熱源作用的有限長熱彈桿的瞬態(tài)響應(yīng).李妍等[29]基于L-S 廣義熱彈擴散理論,建立了考慮材料記憶依賴效應(yīng)和空間非局部效應(yīng)的記憶依賴型非局部廣義熱彈擴散耦合理論.

壓電陶瓷[30-31]廣泛用于各種智能結(jié)構(gòu),由于壓電效應(yīng),常被用作傳感器和致動器等.為描述壓電材料的熱彈行為,Mindlin[32]建立了經(jīng)典熱壓電理論,研究了熱壓電板的熱彈行為; 在1988 年,Chandrasekharaiah[33]對基于熱力學(xué)定律和G-L 熱彈性理論,對Mindlin[32]理論進行了拓展,建立了廣義壓電熱彈耦合的線性理論,其中的熱傳導(dǎo)方程包含溫度變化率,同時在本構(gòu)方程和能量方程中各弓入了一個熱松弛時間因子,描述熱以波的形式以有限速度進行傳播.基于Chandrasekharaiah 理論,He 等[34]等運用拉普拉斯變換,結(jié)合有限元方法,研究了二維廣義熱壓電問題;此外,Majhi[35]提出了一種勢函數(shù),基于L-S 型廣義熱彈壓電理論,研究了半無限長壓電桿受局部熱源作用的動態(tài)響應(yīng);何天虎等[36]基于LS 型廣義熱彈壓電理論,研究了熱源移動時熱壓電桿的動態(tài)響應(yīng); Babaei 和Chen[37]在何天虎等[36]的研究工作基礎(chǔ)上,經(jīng)細(xì)化,進一步研究了受移動熱源作用的有限長熱壓電桿的動態(tài)響應(yīng)問題.

工程中大量材料的形變介于彈性與黏性之間,既具有彈性固體特性,又具有黏性流體特點,即為黏彈性.黏彈性使得材料出現(xiàn)很多力學(xué)松弛現(xiàn)象,如應(yīng)變松弛、滯后損耗等行為.在材料變形時由于分子間有內(nèi)摩擦,分子鏈運動時損耗能量,除彈性形變外,還有黏性形變和損耗,應(yīng)力和形變也不能建立平衡對應(yīng)關(guān)系,而有一個松弛過程,因此出現(xiàn)應(yīng)變滯后于應(yīng)力的現(xiàn)象.在廣義熱彈耦合問題的諸多研究中,結(jié)果表明,位移在彈性波和熱波前不連續(xù)[18-24],這與連續(xù)體力學(xué)的位移連續(xù)性假設(shè)相矛盾.Yu 等[38]的研究工作進一步表明,考慮應(yīng)變率,可消除位移的不連續(xù)性現(xiàn)象.因此,建立廣義熱彈性理論模型時,考慮應(yīng)變松弛,是非常必要的.考慮應(yīng)變率的主旨,便是考慮材料本身的應(yīng)變松弛現(xiàn)象,從而更加真實地反映材料變形機理.

本文在Chandrasekharaiah 廣義壓電熱彈理論的基礎(chǔ)之上,考慮材料變形時的應(yīng)變遲滯現(xiàn)象,通過弓入應(yīng)變率,經(jīng)拓展,建立了考慮應(yīng)變率的廣義壓電熱彈理論.理論中除考慮了應(yīng)變率之外,還考慮了溫度變化率,Mindlin 熱壓電理論[32]以及Green 和Lindsay[13]熱彈性理論都可經(jīng)該理論退化后得到.基于新建立的理論,再次對受移動熱源作用的一維壓電桿的廣義壓電熱彈瞬態(tài)響應(yīng)問題進行了研究,得到了壓電桿中無量綱溫度、位移、應(yīng)力、電勢等的分布規(guī)律,并重點考察了應(yīng)變率對各物理量的影響效應(yīng).

1 基本方程

1.1 理論推導(dǎo)

基于熱彈理論基本方程,借助熱力學(xué)定律,下面來建立考慮應(yīng)變率的廣義壓電熱彈耦合理論.

運動方程

其中,σij是應(yīng)力分量,fi是體力,ρ 是質(zhì)量密度,ui是位移矢量.

應(yīng)變位移關(guān)系

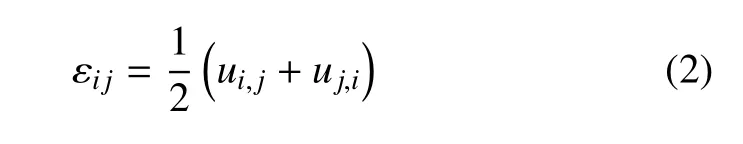
壓電材料能量守恒方程

其中,e是體積比內(nèi)能,qi是熱流矢量,r是內(nèi)熱源,χi j是一個包含應(yīng)變及應(yīng)變率的二階張量,其形式為

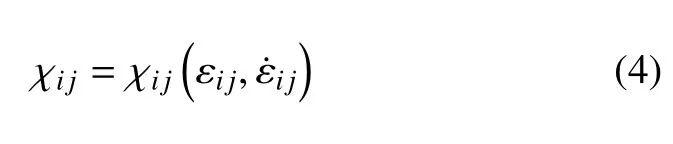
熵不等式

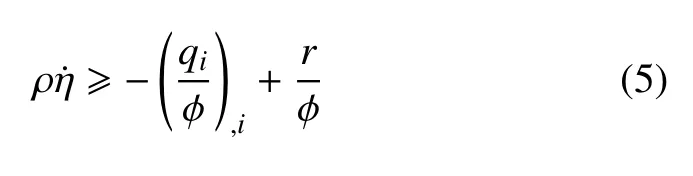
其中,φ 是取決于溫度及其速率的場變量的正標(biāo)量函數(shù),其形式為

高斯方程及電場電勢關(guān)系

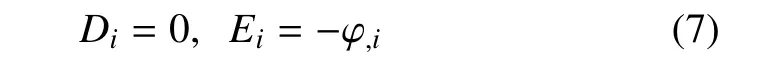
其中,Di是電位移,Ei是電場強度.

從式(4)和式(6)可以得到

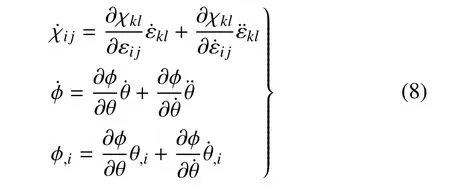
弓入廣義自由能表達式

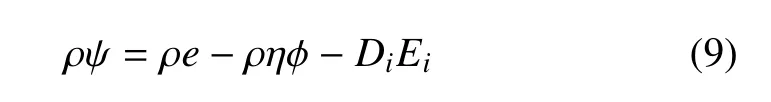
將式(9)代入式(3)中,可以得到能量守恒方程,即熱力學(xué)第一定律

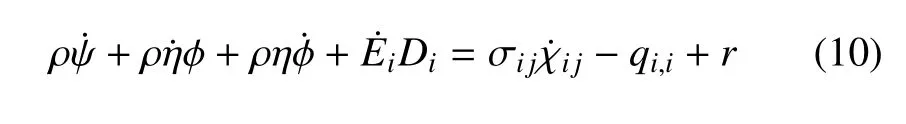
克勞修斯不等式也可以改寫為

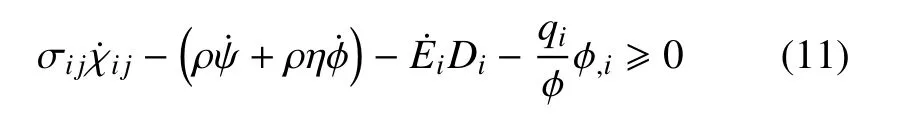
將式(8)代入式(10)和式(11)中,可以得到

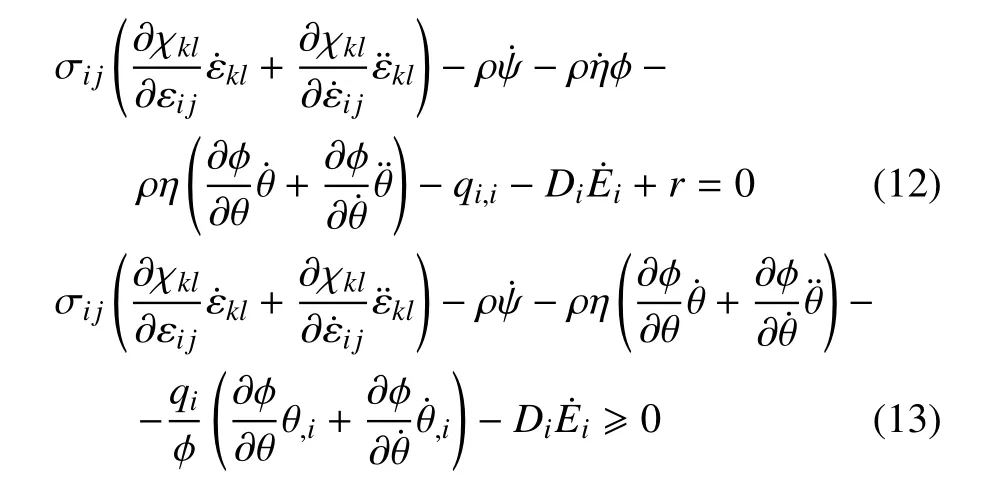
廣義自由能可以假定為如下形式

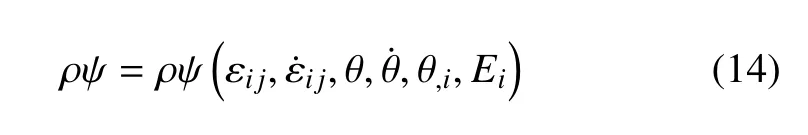
顯然,可以得到

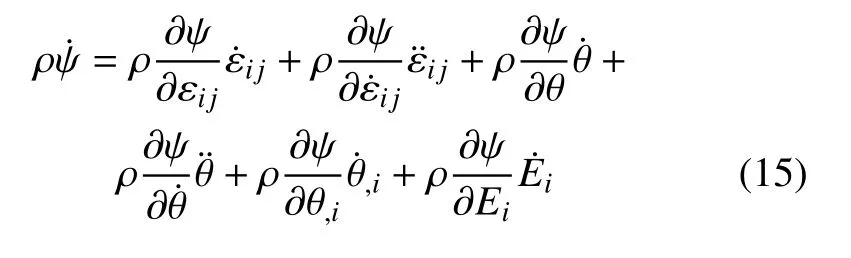
將式(15) 代入式(12) 以及式(13),可以得到如下的本構(gòu)關(guān)系

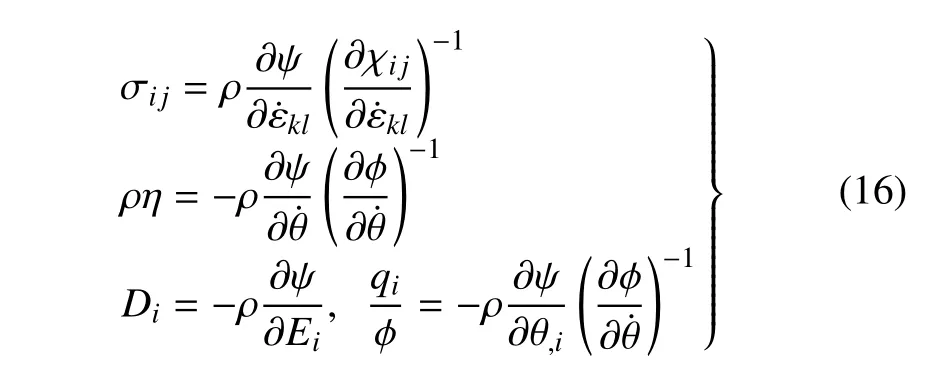
于是,式(12)和式(13)可以被寫作

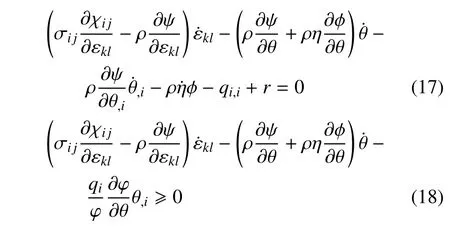
到目前為止,已獲得了考慮應(yīng)變率的壓電熱彈理論的基本方程,即平衡方程(1),幾何方程(2),本構(gòu)方程(16) 和能量守恒方程(17).不等式(18) 會自動成立,稍后將予以證明.

對于線性熱彈性問題,式(4) 和式(6) 可以被寫作

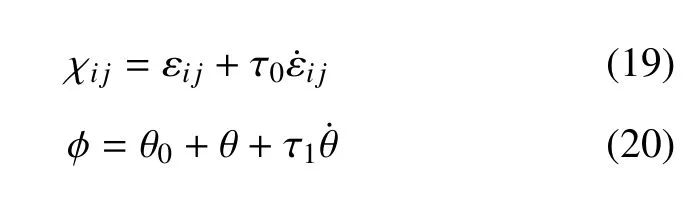
在上兩式中,τ0和τ1是兩個時間遲滯因子,他們之間滿足如下關(guān)系

從式(19)和式(20)中,可以得到

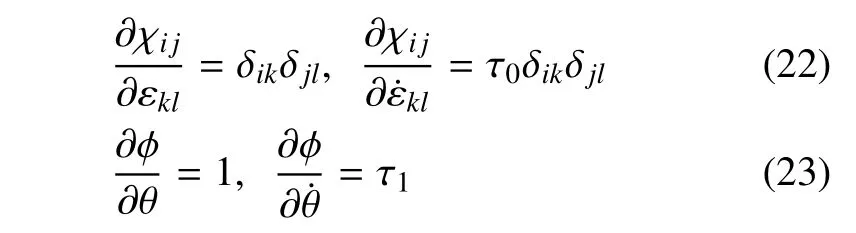
此處,進一步寫出廣義自由能的顯式表達式

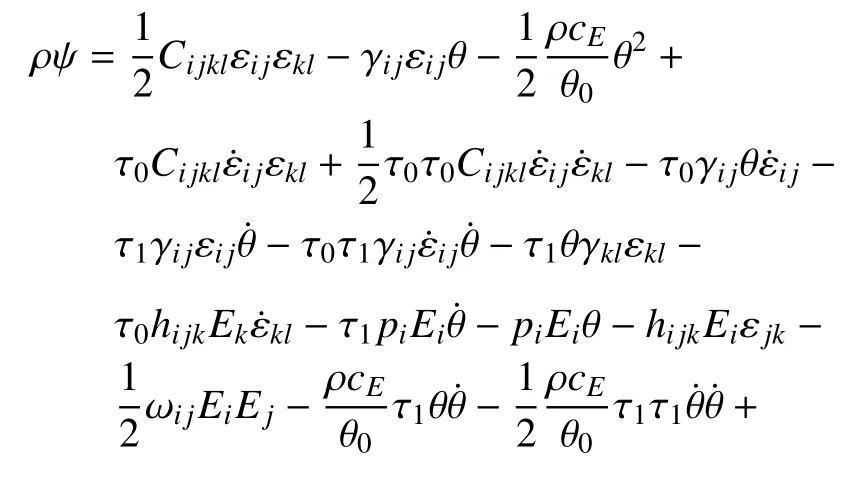
將方程(22)～(24)代入式(26)中,可以得到本構(gòu)方程的顯式表達式,如下所示:

應(yīng)力本構(gòu)方程為

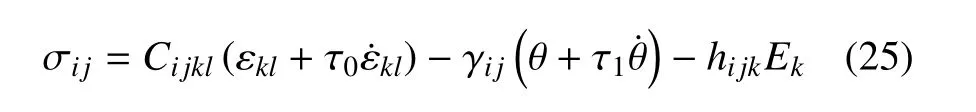
熵本構(gòu)方程

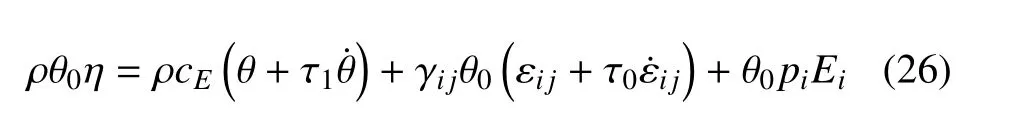
廣義傅里葉定律

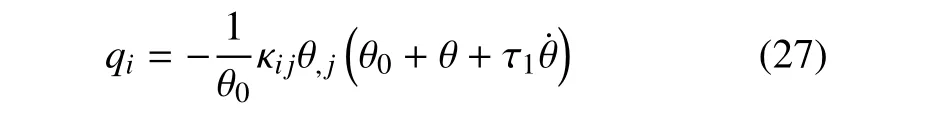
電位移表達式

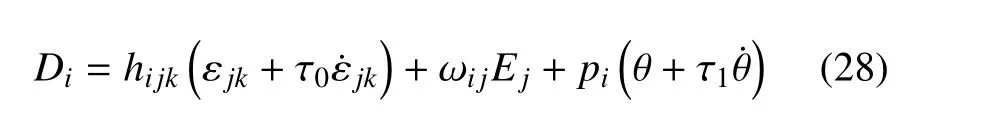
理論推導(dǎo)的最后一步是關(guān)于不等式(18) 的證明,由方程(24)和(25)可得

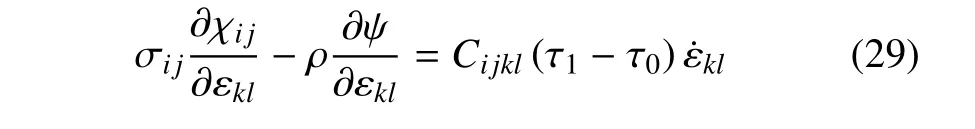
因為τ1≥ τ0＞ 0,因此式(18) 的第一項為正.

同理,由表達式(ρ?ψ/?θ+ρη?φ/?θ)也可以得到

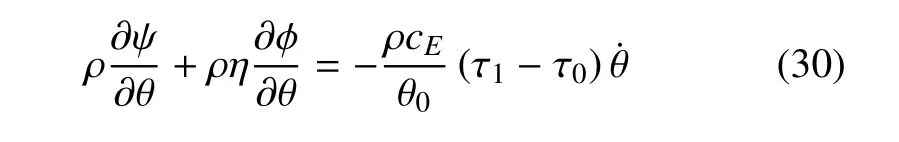
因此,式(18)的第二項也為正,式(18)的最后一項可以被寫作

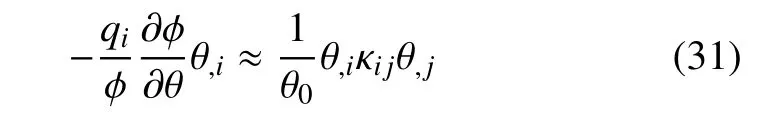
這一項顯然恒正,因此,式(18)自然成立.至此,理論推導(dǎo)結(jié)束.現(xiàn)將如上理論的基本方和歸納如下:

運動方程

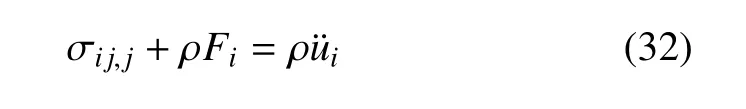
應(yīng)變位移關(guān)系

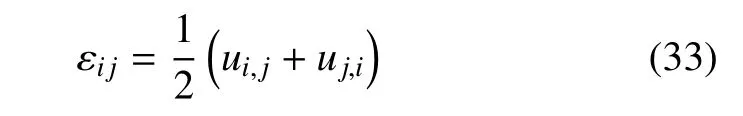
因為θθ,j和相當(dāng)小,如果將它們忽略不計,那么式(28)將退化為傅里葉定律

能量守恒方程

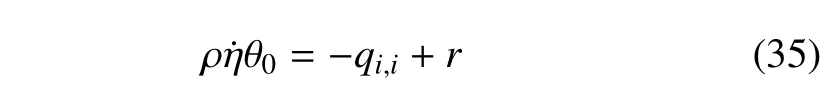
應(yīng)力本構(gòu)方程為

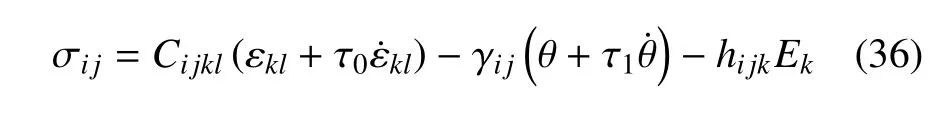
熵本構(gòu)方程

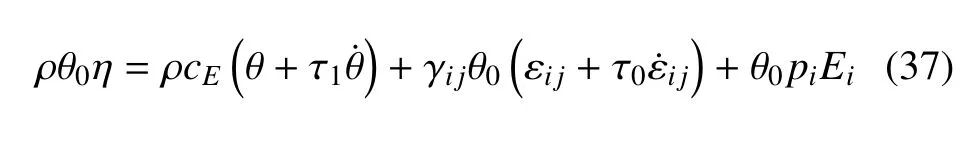
電位移表達式

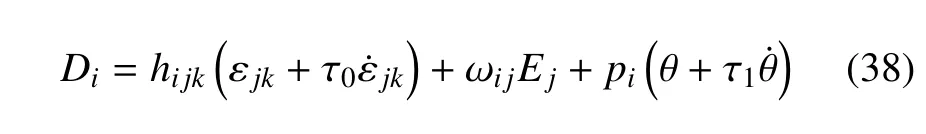
如果不考慮應(yīng)變率,那么當(dāng)前的理論可退化為已有的熱壓電理論.如果是各向同性材料,那么Cijklεkl=2μεi j+λεkkδi j,,γij=(3λ+2μ)αθδij,,κi j=κδi j,其中λ和μ 是拉梅系數(shù),αθ是熱膨脹系數(shù).

1.2 問題描述

基于新建立的考慮應(yīng)變率的廣義壓電熱彈理論,來研究一維壓電桿的壓電熱彈性瞬態(tài)響應(yīng)問題.壓電桿長為L,兩端固定,受沿著軸向的移動熱源作用,如模型圖1 所示.沿桿軸線方向建立一維坐標(biāo)系(x軸向右為正).

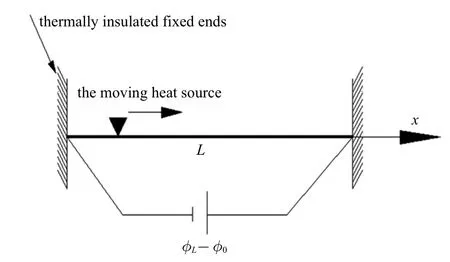
圖1 移動熱源作用下的壓電桿Fig.1 A thermopiezoelectric rod subjected to a moving heat source

在不計自由電荷及體力的情況下,對于一維熱壓電桿,基本方程可寫作

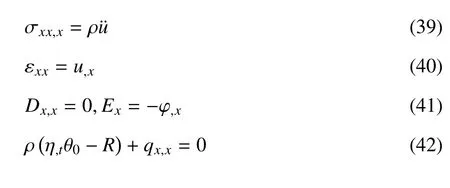
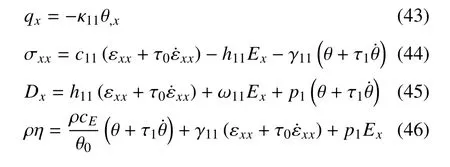
通過以上方程,可得到

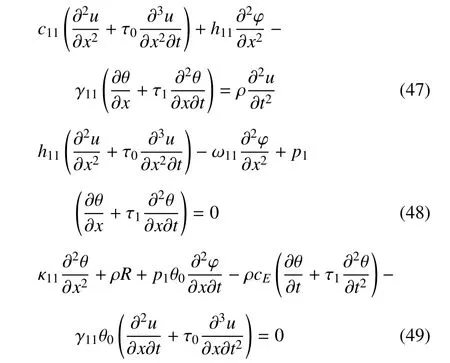
為簡潔起見,弓入如下的無量綱量

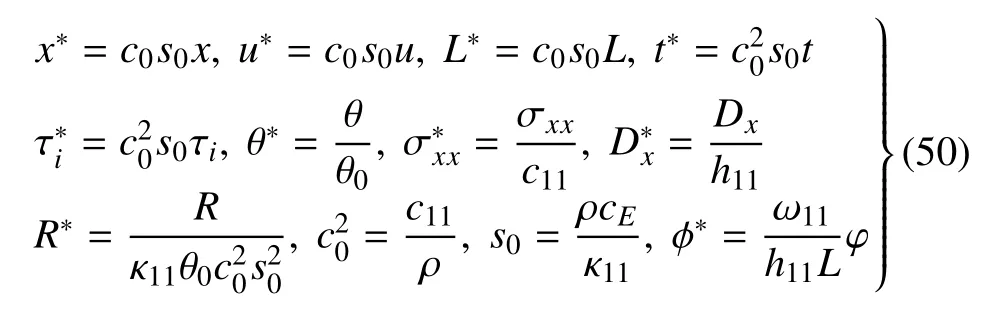
利用以上的無量綱量,式(47)～式(49)變?yōu)?/p>

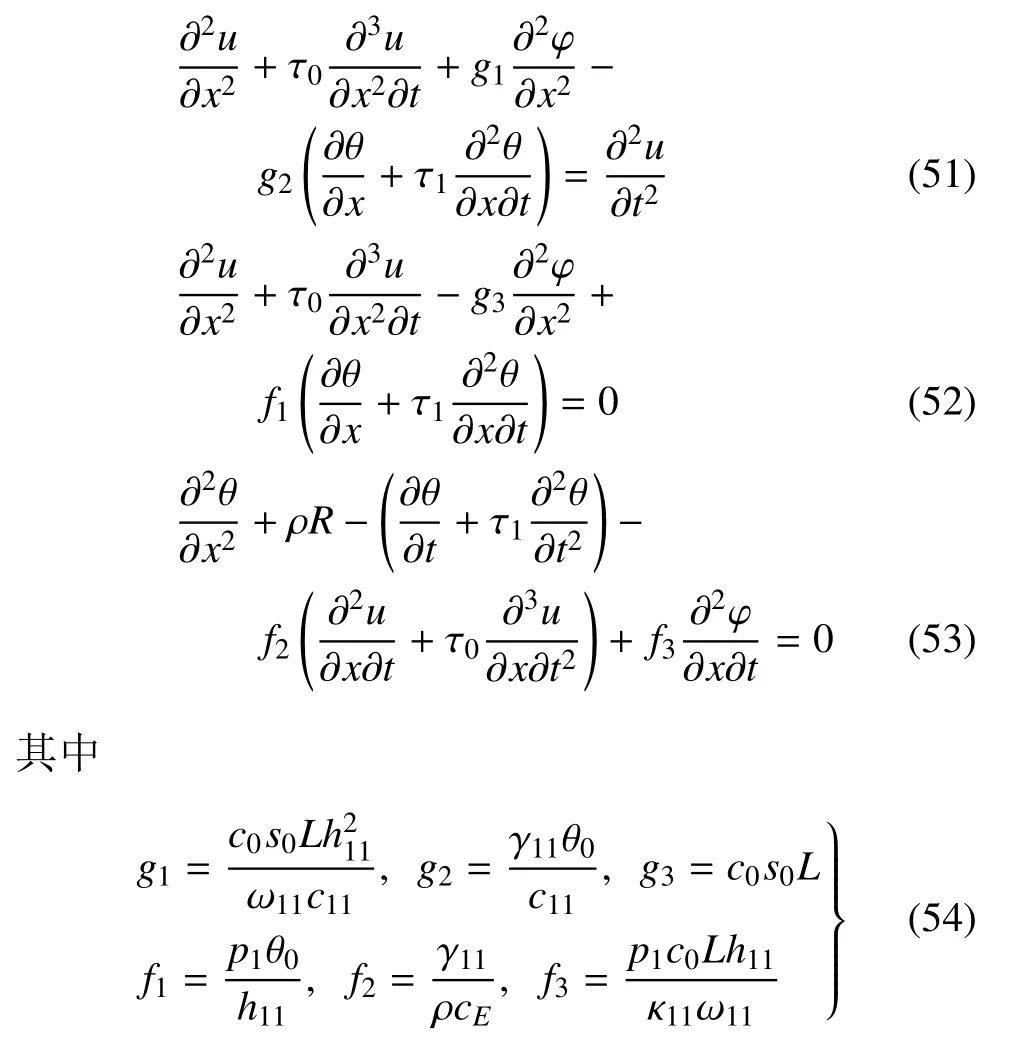
問題的初始條件為

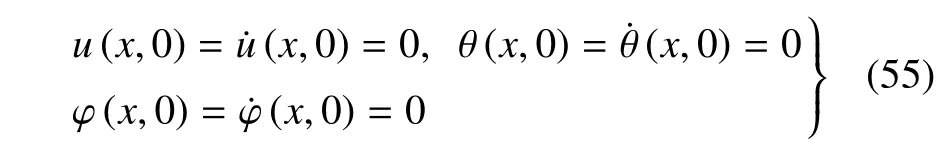
邊界條件為

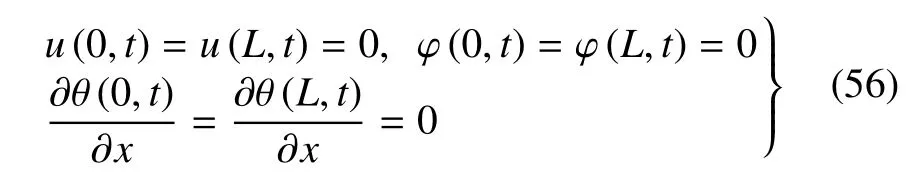
另外,假定無量綱熱源具有以下形式

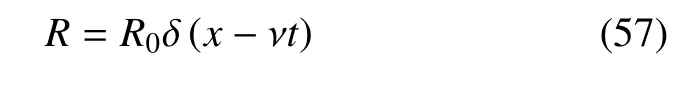
其中,R0是移動熱源的無量綱幅值的大小,δ 是狄克拉函數(shù),ν 是熱源的移動速度.

1.3 在拉氏域內(nèi)的求解

弓入拉普拉斯變換公式

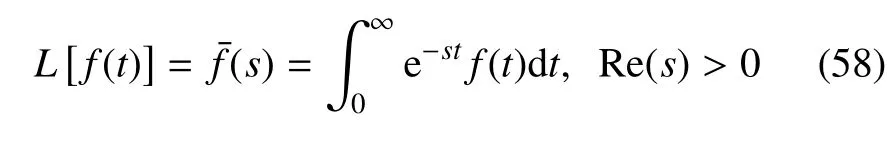
其中,s是拉式變換中的參數(shù),Re 是實部.

對方程(51)～(53)進行拉普拉斯變換

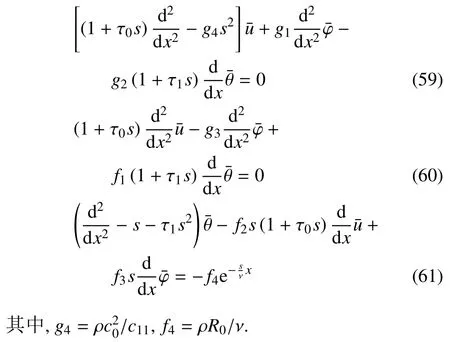
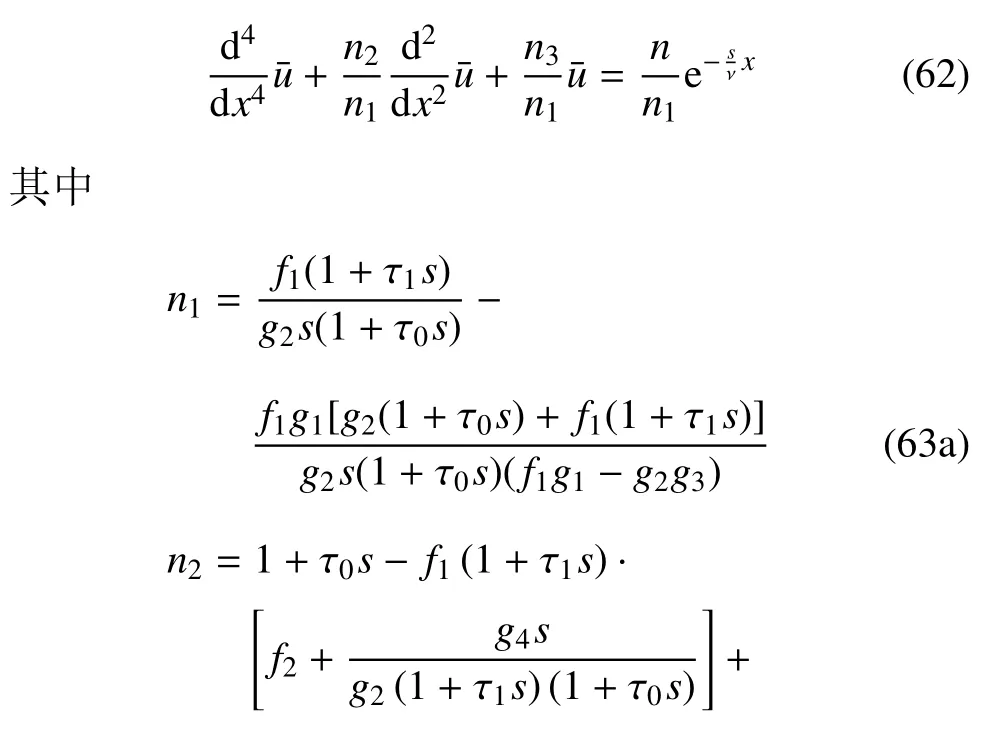
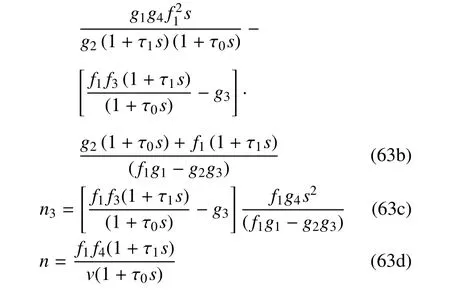
方程(62)的通解為

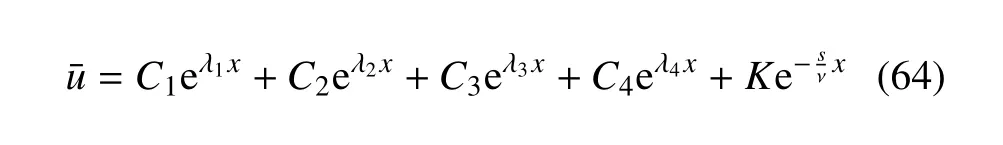
其中C1,C2,C3,C4是待定的常數(shù),K的表達式如下

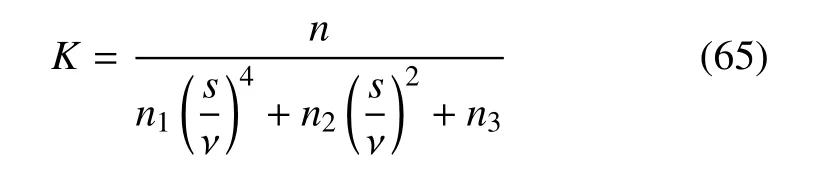
而λ1,λ2,λ3,λ4是如下特征方程的根

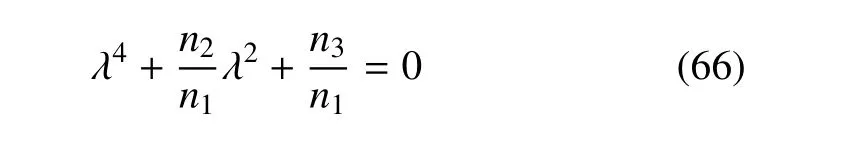
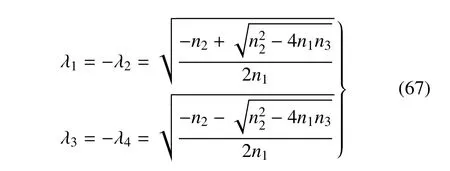
特征根可表示為

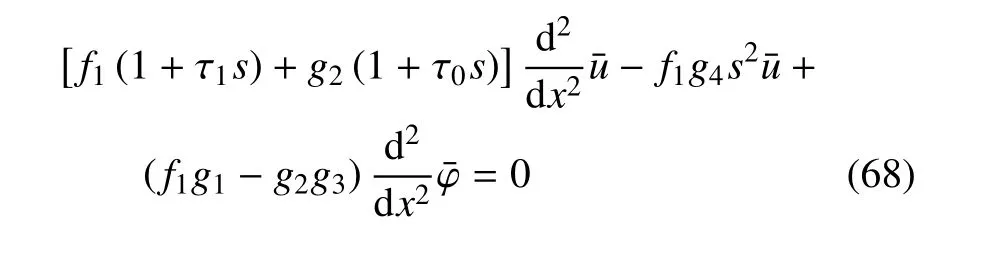
將式(63)代入式(67)中,可得到

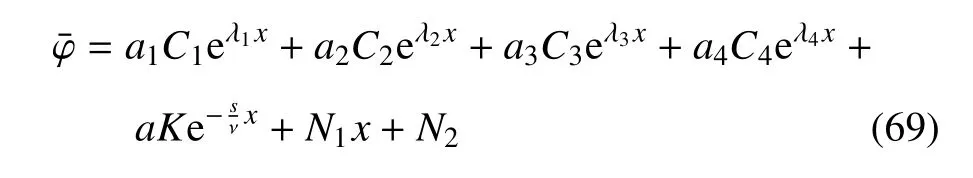
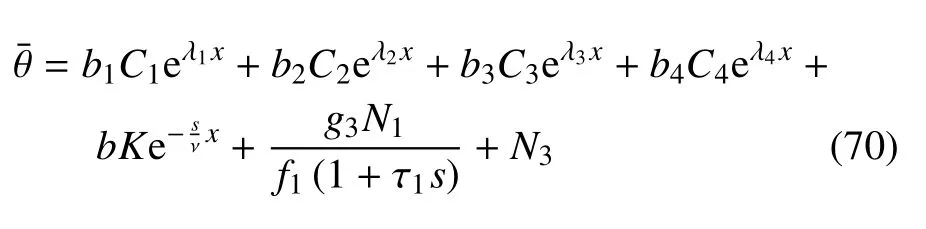
在以上方程中

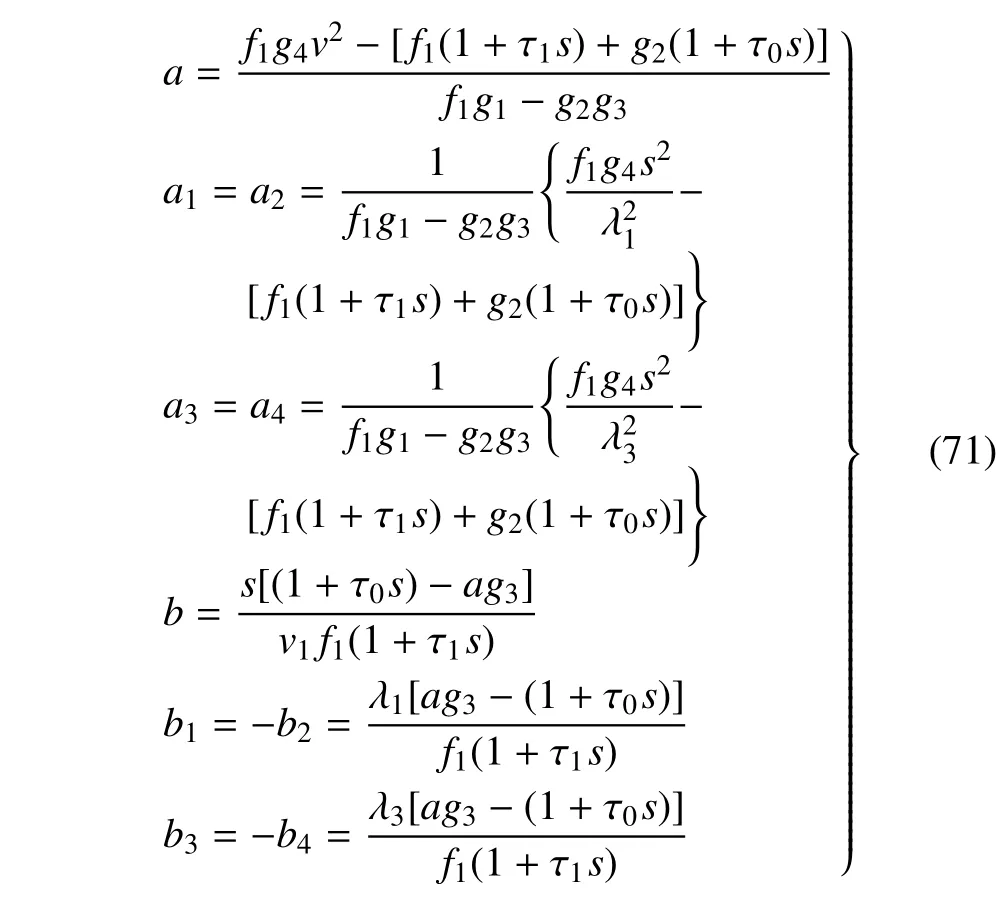
結(jié)合電位移表達式以及應(yīng)力本構(gòu)方程,可得到

其中,i=1,2,3,4.

將式(64)、式(69)、式(70)代入式(61)中,得到

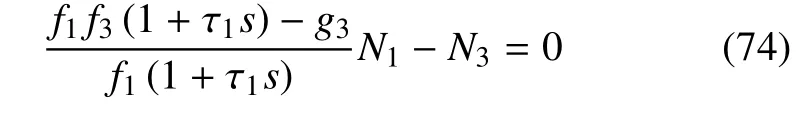
結(jié)合邊界條件(56),可得到

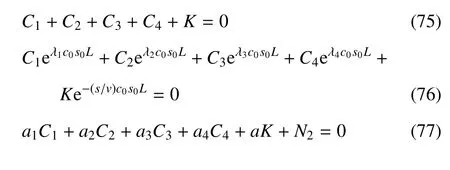
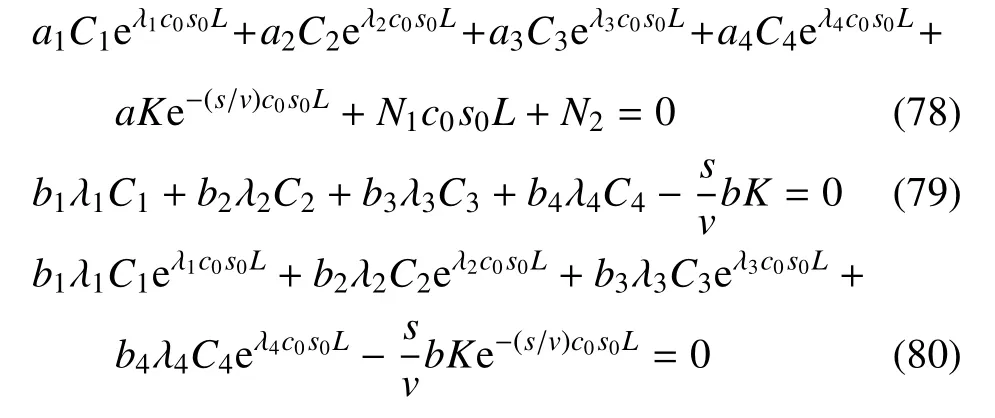
通過求解以上方程,可以得到Ci(i=1,2,3,4),Ni(i=1,2,3) 和K,由于所得表達式過于繁瑣,此處省略未列出.

1.4 拉普拉斯反變換

為得到各物理量在時域中的解,弓入拉普拉斯數(shù)值反變換對各物理量表達式進行反變換,可得

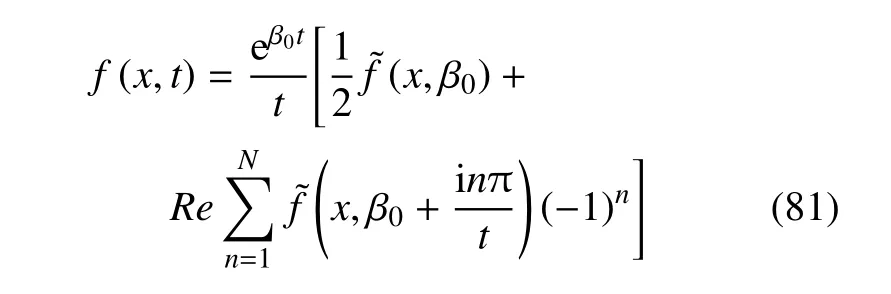
為了能快速收斂,大量的數(shù)據(jù)試驗表明,β0應(yīng)滿足β0t≈4.7[39].

1.5 結(jié)果及討論

為進行數(shù)值計算,需弓入如下的壓電桿材料特性參數(shù):c11=8.674×1010N/m2,γ11=1.16×106N/(m2·K),ρ=2.65×103kg/m3,cE=782 J/(kg·K),h11=0.2 C/m2,ω11=0.392×10-10F/m,p1=4×10-4C/(m2·K),κ11=1.4 W/(m·K).計算中,其他參數(shù)取值如下

經(jīng)計算,得到了壓電桿中無量綱溫度、應(yīng)力、位移、電勢的分布規(guī)律.計算中,著重考察了應(yīng)變率和熱源移動速度對各物理量分布規(guī)律的影響效應(yīng),應(yīng)變率的影響效應(yīng)是通過應(yīng)變松弛時間因子來體現(xiàn)的.計算中,無量綱時間t=0.1,熱松弛時間因子τ1=0.05,應(yīng)變松弛時間因子分別是τ0=0,0.01,0.02,0.03,移動熱源速度取了兩不同值,分別是v=2,3.各物理量的分布圖如圖2～圖9 所示.

圖2 和圖3 顯示無量綱溫度分布規(guī)律.可以看到,同樣的熱源移動速度下,溫度的峰值隨著τ0的增大向左側(cè)移動并且減小.因為左側(cè)有移動熱源的作用,溫度從非零值到達峰值而后逐漸趨于零.同樣的遲滯因子下,溫度會隨著熱源速度的增大而降低,因為一段時間內(nèi)熱源釋放的能量是不變的,導(dǎo)致分配到單位桿長上的能量會隨著熱源速度的增大而減小.每一溫度分布曲線遵循如下規(guī)律:從零開始迅速增加到峰值,然后持續(xù)降低趨近于零.

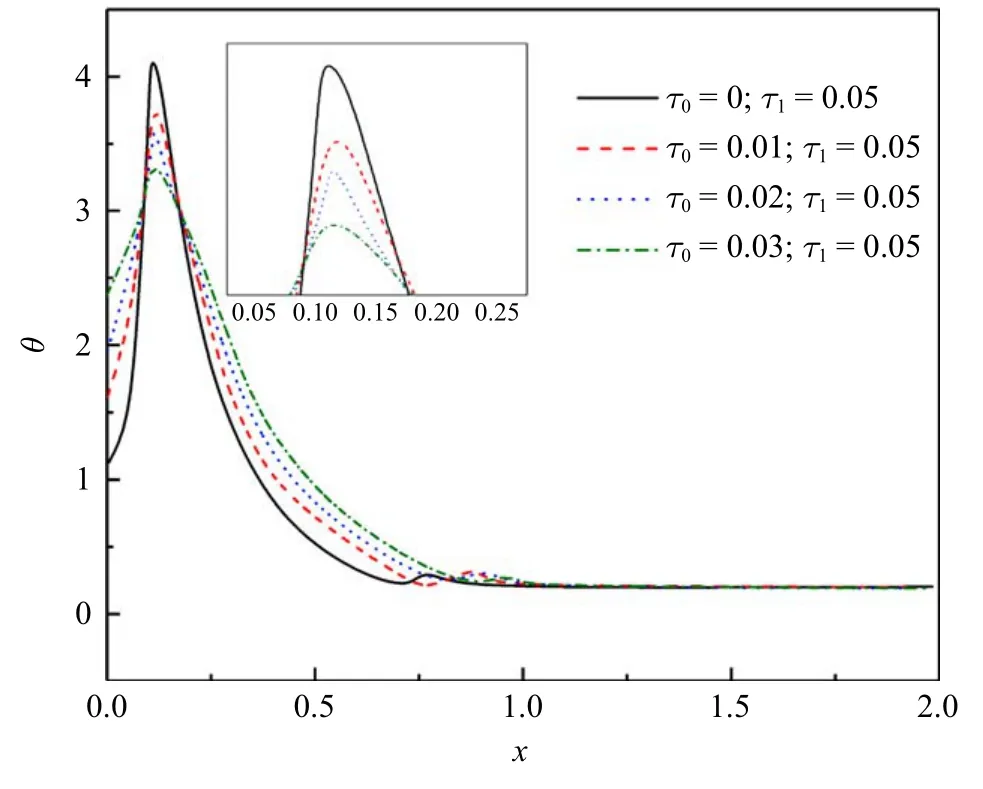
圖2 無量綱溫度(ν=2)Fig.2 The non-dimensional temperature

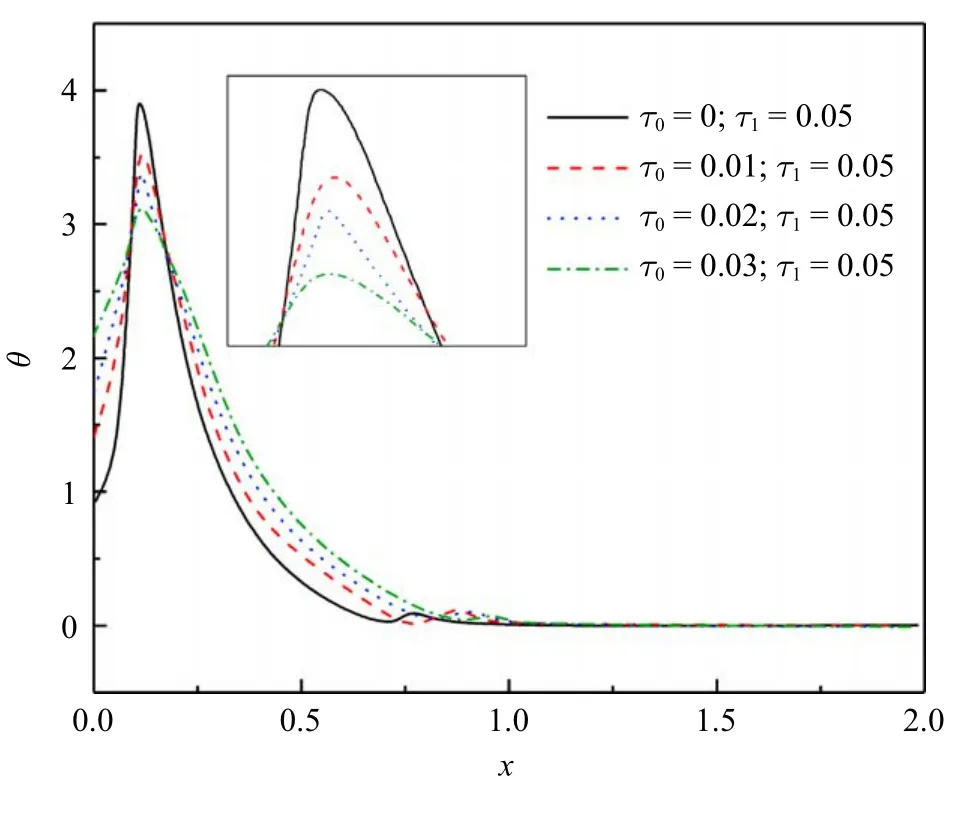
圖3 無量綱溫度(ν=3)Fig.3 The non-dimensional temperature

圖4 和圖5 顯示無量綱應(yīng)力的分布規(guī)律.可以看出桿中出現(xiàn)的是壓應(yīng)力,這是由于熱膨脹和固定端的緣故.在同一熱源速度下,應(yīng)力峰值絕對值會隨著τ0的增加而增加,在同樣的遲滯因子下,應(yīng)力峰值會隨著熱源速度的增大而下降.每一應(yīng)力分布曲線遵循以下規(guī)律:應(yīng)力緩慢增大到達峰值而后持續(xù)降低趨近于零.

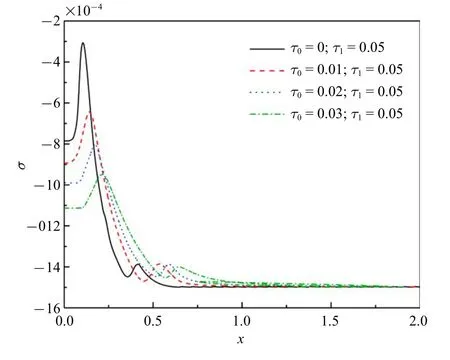
圖4 無量綱應(yīng)力(ν=2)Fig.4 The non-dimensional stress

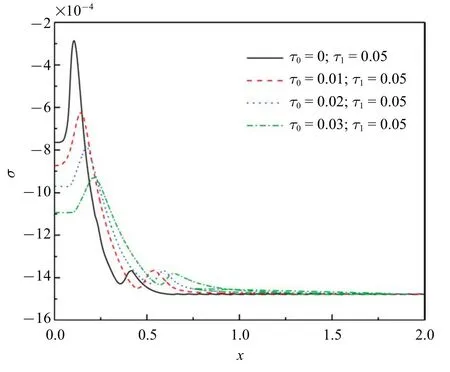
圖5 無量綱應(yīng)力(ν=3)Fig.5 The non-dimensional stress

圖6 和圖7 顯示無量綱位移的分布規(guī)律.從圖中可以看出,同一熱源速度下,位移峰值絕對值隨著τ0的增大而減小,而同一遲滯因子下,位移峰值絕對值會隨著熱源速度的增大而降低.還可以看到,桿的兩端位移仍然為零,這是由于桿的兩端固定.每一位移分布曲線滿足如下規(guī)律:從零開始緩慢增大達到峰值然后逐漸降低趨近于零.

圖8 和圖9 顯示熱壓電桿中無量綱電勢分別在v=2 和v=3 的分布規(guī)律.壓電材料有其特有的性質(zhì),即壓電效應(yīng).由于熱膨脹及桿端固定,桿內(nèi)產(chǎn)生壓電效應(yīng),導(dǎo)致在桿中產(chǎn)生電勢.可以看出,同樣的熱源速度下,電勢的峰值隨著τ0的增大而減小.相同的遲滯因子,不同移動熱源速度下,電勢峰值所在的位置會不同,峰值會隨著移動速度的增大而減小.每一電勢分布曲線遵循以下規(guī)律:從零開始緩慢增大到峰值而后持續(xù)降低趨近于零.

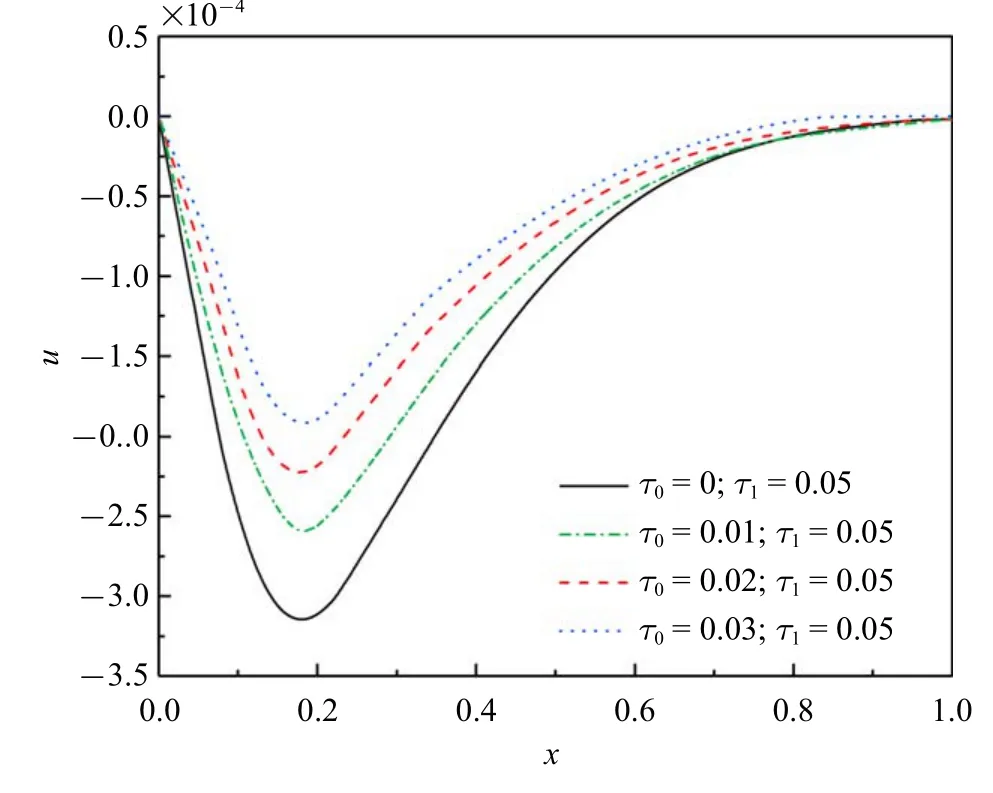
圖6 無量綱位移(ν=2)Fig.6 The non-dimensional displacement

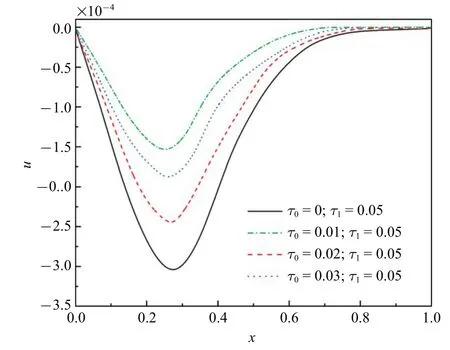
圖7 無量綱位移(ν=3)Fig.7 The non-dimensional displacement

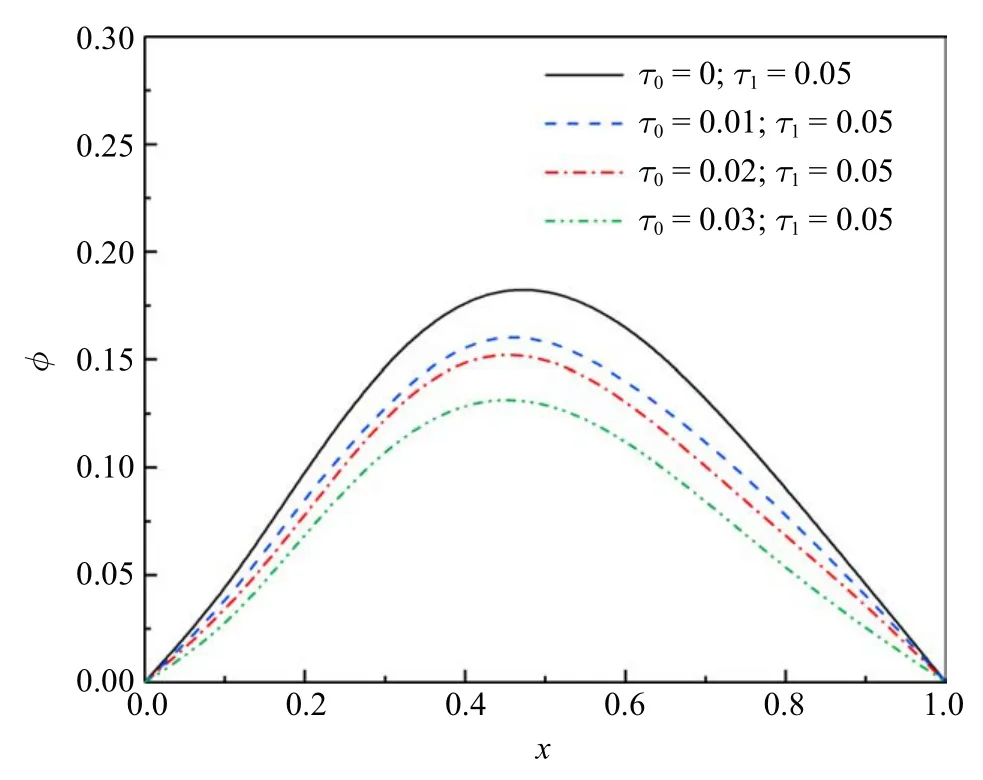
圖8 無量綱電勢(ν=2)Fig.8 The non-dimensional electric potential

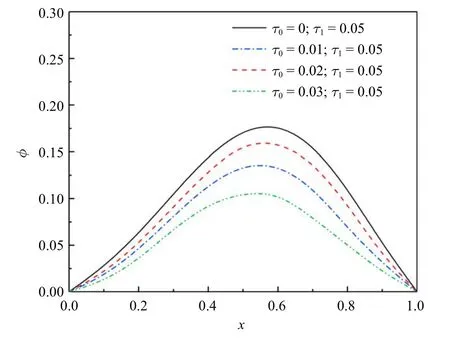
圖9 無量綱電勢(ν=3)Fig.9 The non-dimensional electric potential

2 結(jié)論

本文借助熱力學(xué)定律,建立了考慮應(yīng)變率的廣義壓電熱彈理論,并應(yīng)用該理論研究了兩端固定的一維壓電桿在移動熱源作用下的瞬態(tài)響應(yīng)問題.得到了無量綱電勢、溫度、應(yīng)力、位移在不同熱源速度下的分布規(guī)律并作圖說明.研究了不同應(yīng)變遲滯因子τ0對瞬態(tài)響應(yīng)的影響.結(jié)果表明:

(1)在同一熱源速度下,無量綱電勢的峰值會隨著τ0的增大而減小;同時,保持τ0不變時,電勢的峰值隨著熱源速度的增加而降低;

(2)在同一熱源速度下,無量綱溫度的峰值會隨著遲滯因子τ0的增大而減小;同樣的遲滯因子和溫度會隨著熱源速度的增大而減小;

(3)同一熱源速度下,桿內(nèi)產(chǎn)生壓應(yīng)力,無量綱應(yīng)力的峰值隨著τ0的增大而增大;在同樣的遲滯因子下,應(yīng)力峰值會隨著熱源速度的增大而下降;

(4)在同一熱源速度下,位移峰值絕對值隨著τ0的增大而減小;而同一遲滯因子下,位移峰值絕對值會隨著熱源速度的增大而降低.