一類Duffing 型系統的不動點混沌和Fold/Fold 簇發現象及機理分析1)

陳婭昵 孟文靜 錢有華

(浙江師范大學數學與計算機科學學院，浙江金華 321004)

引言

在非線性動力學中有一類問題中有一些參數隨著時間的推移而緩慢變化，造成了在同一個系統中存在兩個或兩個以上的時間尺度，這也被稱為多時間尺度問題[1-3].多時間尺度問題具有廣泛的應用背景，包括生物網絡系統中的神經放電模式[4]、金屬氧化反應等.但由于其復雜性，很難用準靜態解、奇異攝動法等來研究其解析解，一般只能得到近似的數值解，因此數值分析的方法應運而生.通過數值模擬發現多時間尺度相比于單一的時間尺度具有更復雜的系統表現，如混合模式振蕩[5-10].

混合模振蕩又稱簇發振蕩，是一種復雜的振蕩模式，它的特征是小振幅振蕩和大振幅振蕩的結合，可以用快速和緩慢的子系統來描述.當系統處于小幅度振蕩時，系統表現出靜息狀態；當系統經過相關分岔點時會突然失去平衡，進入大幅度振蕩，此時系統表現出活躍態.隨著慢變量的引導，系統又會從不平衡走向平衡，由活躍態走向靜息態，振幅也從大幅度的振蕩變為小幅度的振蕩，而一旦達到分岔點時，會類似地出現之前的現象.此時的系統就是在靜息態和活躍態之間不停地跳躍，稱為混合模式振蕩.

混合模式振蕩也會出現在快慢耦合系統中.Rinzel[11]提出了利用凍結子系統的方法來解釋混合模式振蕩的想法，這就是我們所知道的快慢分析，它的應用取得了很大的效果.在Izikevich[12]的工作中，創建了混合模式振蕩的分類.在快速慢分析的基礎上，在研究多時間尺度的系統中，眾多學者研究了快慢系統中混合模式振蕩出現的機理.例如：Qian 等[13]研究了含兩個慢變量的耦合系統的混合振蕩模式，討論了不同時間尺度下的系統動力學行為以及時滯對系統行為的影響；Qian 等[14]研究了單參數激勵和雙參數激勵下的兩自由度非線性耦合的Duffing 方程，利用快慢分析方法對耦合系統進行離散，通過數值模擬發現系統會產生簇發振蕩現象，并討論了相關的振動動力學行為；Han 等[8]使用緩慢參數和外部激勵來模擬兩個緩慢變化的周期參數，并研究了不同時間尺度下的動態響應問題；Zhang 等[15]使用雙穩態不對稱復合材料層合板對兩個慢參數激勵的系統以及動態跳躍現象進行了實驗和理論分析，提出了一種利用時變原理曲率描述雙穩態非對稱層合板動態切換現象的新方法；Chen 等[16]展現了具有周期激勵的耦合振蕩器的弛豫振蕩，以典型分叉模式為例，討論了外激勵變化對動態響應的影響，在靜止狀態和重復尖峰振蕩之間交替可以得到簇發振蕩；Li 等[17]在具有緩慢周期性參數激勵的Duffing 振蕩器中，通過數值模擬發現了一種稱為周期混沌運動的新型響應，稱為不動點混沌；Lin 等[18]研究了一種簡單的三元記憶電路周期簇發振蕩的分岔機理；Wang 等[19]也研究了簡單的自主記憶電路，分析了其對稱性、耗散性和平衡穩定性.茍向鋒等[20]基于參數平面的耦合研究了單自由度齒輪傳動系統安全盆侵蝕與分岔；畢勤勝等[21-22]討論了不同系統的簇發振蕩及其分岔行為；張正娣等[23-24]對于幾類非光滑的系統進行了簇發振蕩分析；Han 等[25-26]對Duffing 系統進行研究，發現了時滯周轉引起的新的簇發振蕩類型，叉式翻轉遲滯簇發振蕩以及復合叉式遲滯簇發振蕩.

本文通過構造參數空間來解釋簇發現象產生的機理.下面簡述這一理論的發展過程.

Rinzel 等[11,27]是第一個利用“解剖”方法來研究快慢系統的簇發振蕩，他認為簇發振蕩取決于所遇到的分岔，即通過研究慢變量經歷不同分岔時產生的躍遷可以對簇發振蕩行為進行分類.1995 年，Bertram 等[28]研究了Chay-Cook 模型的兩參數分岔圖，他們發現這可以看成是三參數焦點型退化Takens-Bogdanov 奇點展開的一個切片.2000 年，Izhikevich[12]發現簇發振蕩開始和偏移時的不同位置會導致動態響應發生質的變化.并且基于起始/偏移分岔對來編譯可能的簇發振蕩分類法.2008 年，Stern 等[29]發現其中一種亞臨界Hopf 簇發振蕩，它不在余維三奇點展開中出現.2016 年，Osinga 等[30]，研究了生物學和數學的交叉流：偽高原簇發的余維.在一個立方Li′enard 系統的分岔中，發現Fold/homoclinic 簇發振蕩與Fold/subHopf 簇發振蕩具有非常相似的潛在分岔圖，但它不是余維三的，因此可以預測具有余維四.最后通過展示了一個雙退化的Bodganov-Takens 點的部分展開中識別出一個三維切片，并證明這個余維四奇異性導致了幾乎所有已知的簇發振蕩類型.2017 年，Saggio 等[31]提出幾乎可以產生所有種類的簇發振蕩模型，模型包含兩個子系統，對于快子系統，可使用高余維奇點平面展開.在分岔圖中，可以確定簇發振蕩所需穿過正確分岔序列的路徑.而慢子系統沿路徑來回引導快子系統.

本文在文獻[15]的基礎上，針對一類含有兩個慢變量的系統使用數值模擬的方法研究了在參數較大的情況下產生的分岔.本文使用數值模擬和基于參數空間的理論分析研究了在參數較小的情況下系統存在雙穩態和Fold/Fold 簇發振蕩現象，并為控制該系統得到簇發振蕩現象提供了參考數據.其中對參數大小的界定標準如下：以1 為界，若參數大于1，認為它是較大的；小于1，則認為它是較小的.

1 不動點混沌

在這一部分我們主要分析了一類含有兩個慢變量的Duffing 系統在參數較大情況下的動力學行為.通過數值模擬，得到了系統的時間歷程圖和相位圖.研究表明系統存在不動點混沌，并且隨著參數的變化，不動點混沌會表現為單支存在或者雙支合并形式.之后本文進一步解釋了系統不動點混沌產生的機理.

考慮如下系統

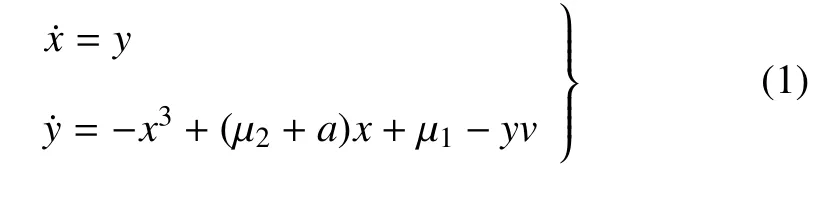
其中，μ1=β1cos(ω1t),μ2=β2cos(ω2t).β1,β2表示振幅，v表示阻尼系數，ω1,ω2表示頻率，v,β1,β2被認為是擾動參量.文獻[15]對該系統在實驗上發現了雙穩態現象，并從理論上解釋了雙穩態現象及動態跳躍現象.

首先假設a=0，則系統(1)變為

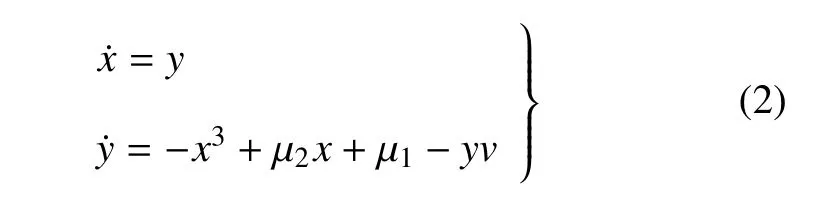
對于系統(2)，為不失一般性，選擇β1,β2＞0 并假設ω1=ω2=ω.由于剛度和外激勵項是周期性時變的，因此它在一個半周期是正的，在另一個半周期是負的.由于剛度和外激勵項的周期性時變性，導致系統產生高度復雜和不尋常的動態響應，包括周期混沌運動的新現象.

固定β1=0.1，β2=6.257 5，v=0.3 時，當ω=0.7 和ω=0.135 5 時，混沌吸引子存在，如圖1 和圖2 所示.

文獻[17]介紹了不動點混沌，這是一種新的混沌現象.它的典型特點是存在一個不動點.對于ω ?1，系統具有兩個不同的時間尺度，一個是快時間尺度，一個是慢時間尺度.當ω=0.135 5，β1=0.1，β2=3.3，v=0.3 時，兩個混沌吸引子共存.這些吸引子的最大Lyapunov 指數是正的，表明它們確實是混沌的.而當β2改變時，兩個共存的吸引子會分開，出現單獨左支或者單獨右支的情況.下面保持其他參數不變，而只改變β2分別為2.0 和2.7.

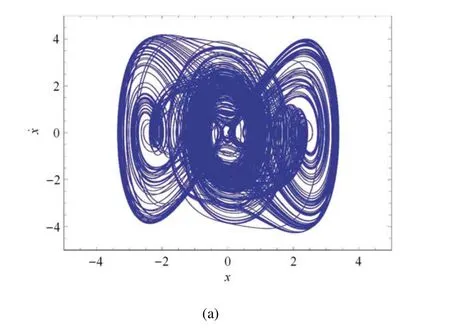
圖1 β1=0.1,β2=6.257 5,v=0.3，當ω 分別取0.7 和0.135 5 時系統(2)表現出混沌吸引子Fig.1 β1=0.1,β2=6.257 5,v=0.3，system(2)shows chaotic attractors when ω=0.7 and ω=0.135 5,respectively

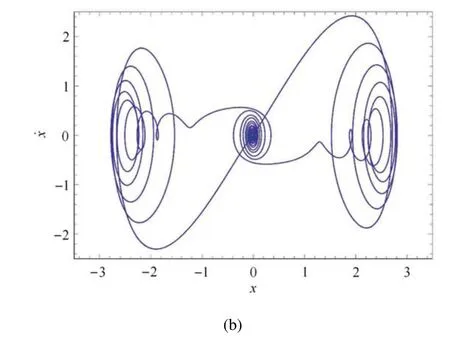
圖1 β1=0.1,β2=6.257 5,v=0.3，當ω 分別取0.7 和0.135 5 時系統(2)表現出混沌吸引子(續)Fig.1 β1=0.1,β2=6.257 5,v=0.3，system(2)shows chaotic attractors when ω=0.7 and ω=0.135 5,respectively(continued)

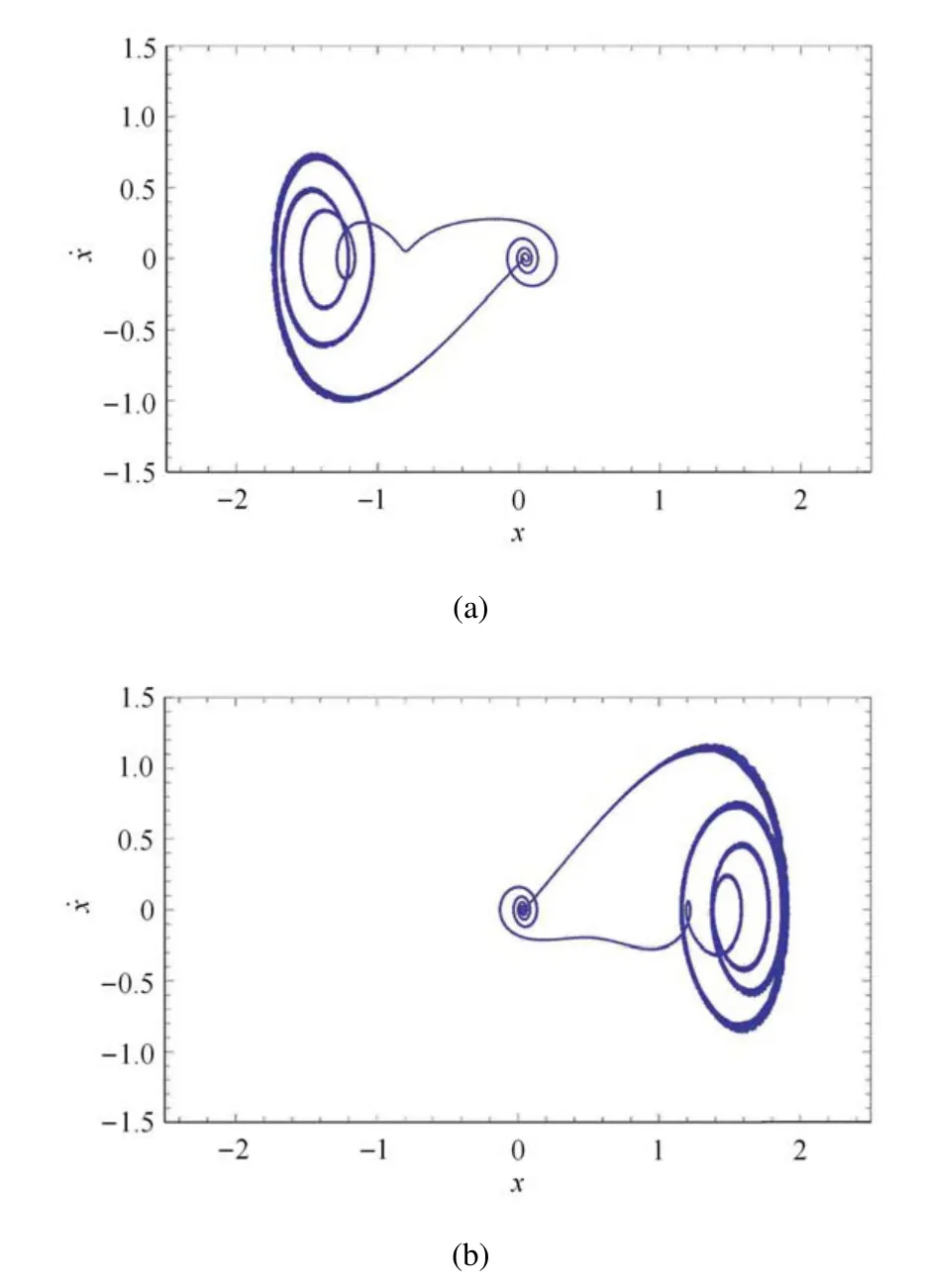
圖2 ω=0.1355,β1=0.1,v=0.3，系統(2)在β2=2.0 時表現出單獨左支行為，在β2=2.7 時表現出單獨右支行為Fig.2 ω=0.1355,β1=0.1,v=0.3，system(2)shows the behaviors of left branch alone with β2=2.0 and right branch alone with β2=2.7

為進一步研究不動點混沌的機理，討論了快慢系統的分岔行為.對于ω ? 1，周期激勵μ1=β1cos(ωt)，μ2=β2cos(ωt)分別在[-β1,β1]和[-β2,β2]之間變化緩慢.將μ1,μ2近似地視為一個常數，并將cos(ωt)用作自治系統的分岔參數.

系統(2)的靜態平衡解滿足

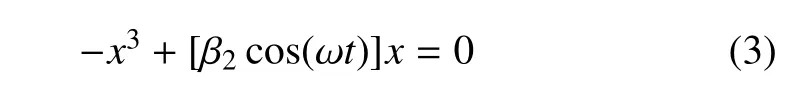
當cos(ωt) ＜ 0 時，系統只有一個穩定平衡點；當cos(ωt) ＞0 時，平衡解由于發生分岔而失穩，產生了一對對稱穩定的分岔解，；因此pitchfork 分岔發生在cos(ωt)=0，記為PF.圖3給出了系統的離散分岔圖.

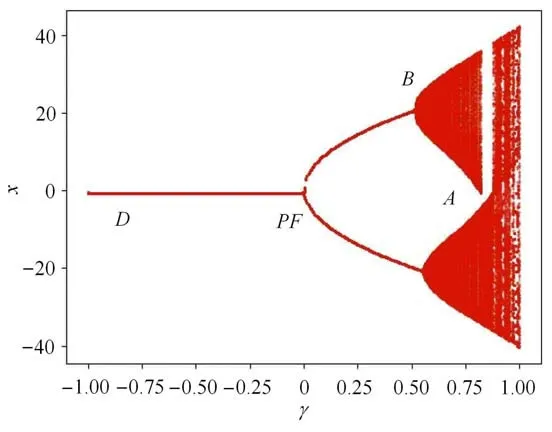
圖3 β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3 時系統(2)的離散分岔圖Fig.3 Discrete bifurcation diagram of system(2)when β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3

取β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3 來說明不動點混沌機理.圖3 顯示了規則運動和混沌變化的過程.與上圖對應，我們可以看到，A所在的地方是未被紅色區域覆蓋，此時系統的狀態是靜默的.在A的右側，已被紅色覆蓋，A可以跳躍到上分支或者是下分支，變成了尖峰狀態.因此點A是靜止狀態到尖峰狀態的轉換點.隨著激勵的增大，系統在穩定分支的周圍擁有尖峰狀態.當激勵達到最大值，它們開始改變方向，并在同一穩定分支上移動，隨著激勵的減小而停留在靜默狀態.當軌跡到達分岔點PF時，它可能被左穩定點吸引，并開始接近穩定平衡點.激勵達到最小值，它處于D點.此時，它重新向A點移動，通過平衡點(0，0).然后平衡點(0，0)變得不穩定，逐漸到達B點.在軌跡集合中顯示的隨機性很可能是因為當系統被吸引到穩定平衡(0，0)時，響應變量x和y是非零的并且很小.在數值計算或實驗中，這樣的小數字實際上是隨機的.因此，離開平衡(0，0)的軌跡在每個周期都有不同的初始條件.對該系統中的初始條件的敏感性顯然是混沌的一種性質，所以構成了一個混沌運動.圖4 中顯示的最大Lyapunov 指數從0.3 變化到小于0.01.它顯示了系統豐富的動力學性質，暗示了系統的復雜性.因此，我們對該系統進行了一系列的數值研究.圖4 也說明了這一點，當最大Lyapunov 指數大于0 時，表示系統存在混沌現象.

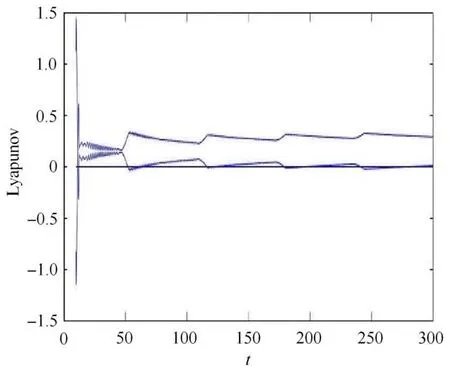
圖4 β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3 時系統(2)的最大Lyapunov 指數Fig.4 Maximum lyapunov exponent of system(2)when β1=0.1,β2=6.257 5,ω=0.135 5,v=0.3

2 Fold/Fold 簇發振蕩

在這一部分，主要考慮系統(2)中當兩個慢變量的振幅β1＜1,β2＜1 時系統簇發振蕩現象.系統(2)來源于文獻[15].文獻[15]從理論和實驗兩個方面研究了雙穩態不對稱層合板在外激勵的作用下的動態跳躍現象和非線性振動行為，并且發現雙穩態不對稱層合板在位于中間的不穩定平衡位置時附近會有兩個穩定態振動，分別位于上穩定態分支或下穩定態分支.如圖5 所示.當系統從一穩定分支跳躍到另一穩定分支時，它就會產生出文獻[15]所說的動態跳躍現象，從理論上分析也就是Fold/Fold 簇發振蕩.本文對文獻[15]中的系統考慮了不同參數的情況.

在快慢系統中，會產生一系列的簇發振蕩、尖峰和靜止的周期性變化.其中，一個或多個慢變量通過一系列分岔傳遞快變量，這些分岔介入導致振蕩和穩態之間的轉換.在以往的研究中發現折疊分岔是余維一的，而兩個折疊分岔曲面相交會形成二余維的尖點，如圖6 所示.本文通過折疊分岔來解釋Fold/Fold 簇發振蕩現象.

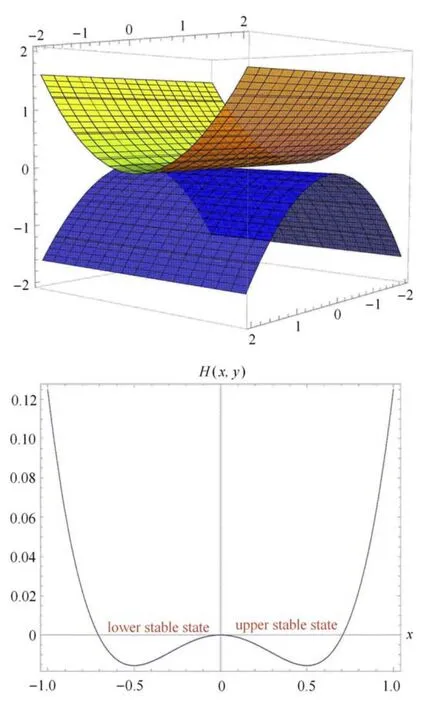
圖5 雙穩態不對稱層合板與動態跳躍現象Fig.5 Bistable unsymmetrical composite square panel and dynamic fracture phenomenon

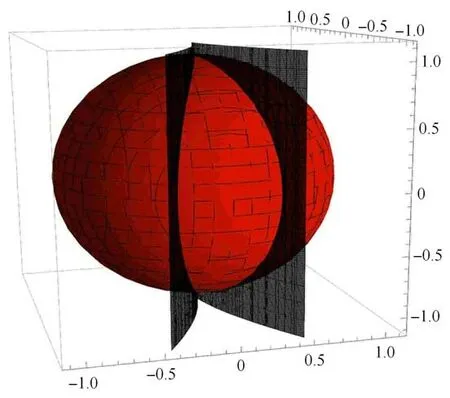
圖6 以單位球面為邊界的分岔Fig.6 Bifurcation with unit sphere as boundary

此時系統寫作快慢系統形式

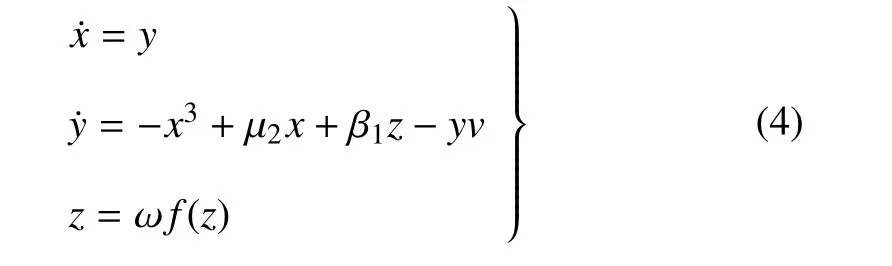
其中

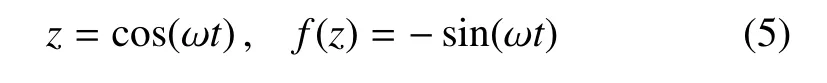
現在將系統視為一個質點，它受到作用在兩個垂直方向μ1，μ2軸上的簡諧運動，此時這兩個分振動可以表示為

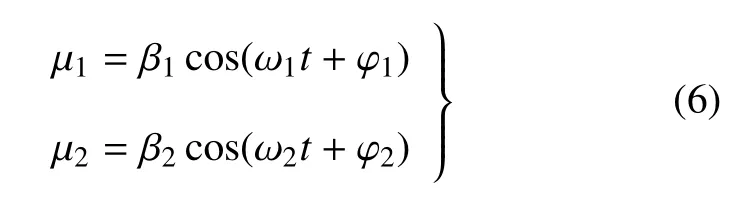
其中，ω1:ω2=1 :2，φ1-φ2=π.可以給出軌跡方程如下

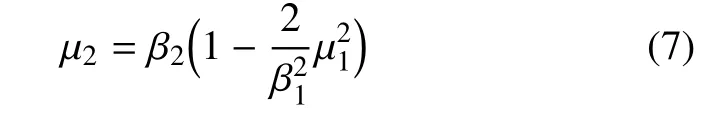
此時任意的β1，β2，a都會產生Fold/Fold 簇發振蕩，見圖7.下面將詳細介紹系統是如何運動的.

在這里可以將相圖與時間歷程圖對應起來解釋更微觀的情況.圖7 顯示了簇發振蕩，當β1=0.38,ω=0.03,v=0.1 時系統發生Fold/Fold 簇發振蕩，在這里可以發現，吸引子在兩個平衡點F1，F2附近振蕩.F1位于平衡上分支，F2位于平衡下分支.其中的兩段尖峰振蕩分別對應于平衡點附近，被平衡點F1，F2之間的跳躍運動所連接.在時間歷程圖上，發現軌跡可以在兩個重復的尖峰振蕩S P+，S P-之間跳躍，這一運動是對稱的.從更深層次的來看，重復尖峰振蕩的頻率在改變，那是因為相關平衡點在平衡分支上的位置變化，造成了特征值的變化，使得S P±隨著慢變參量ω 的變化而變化.

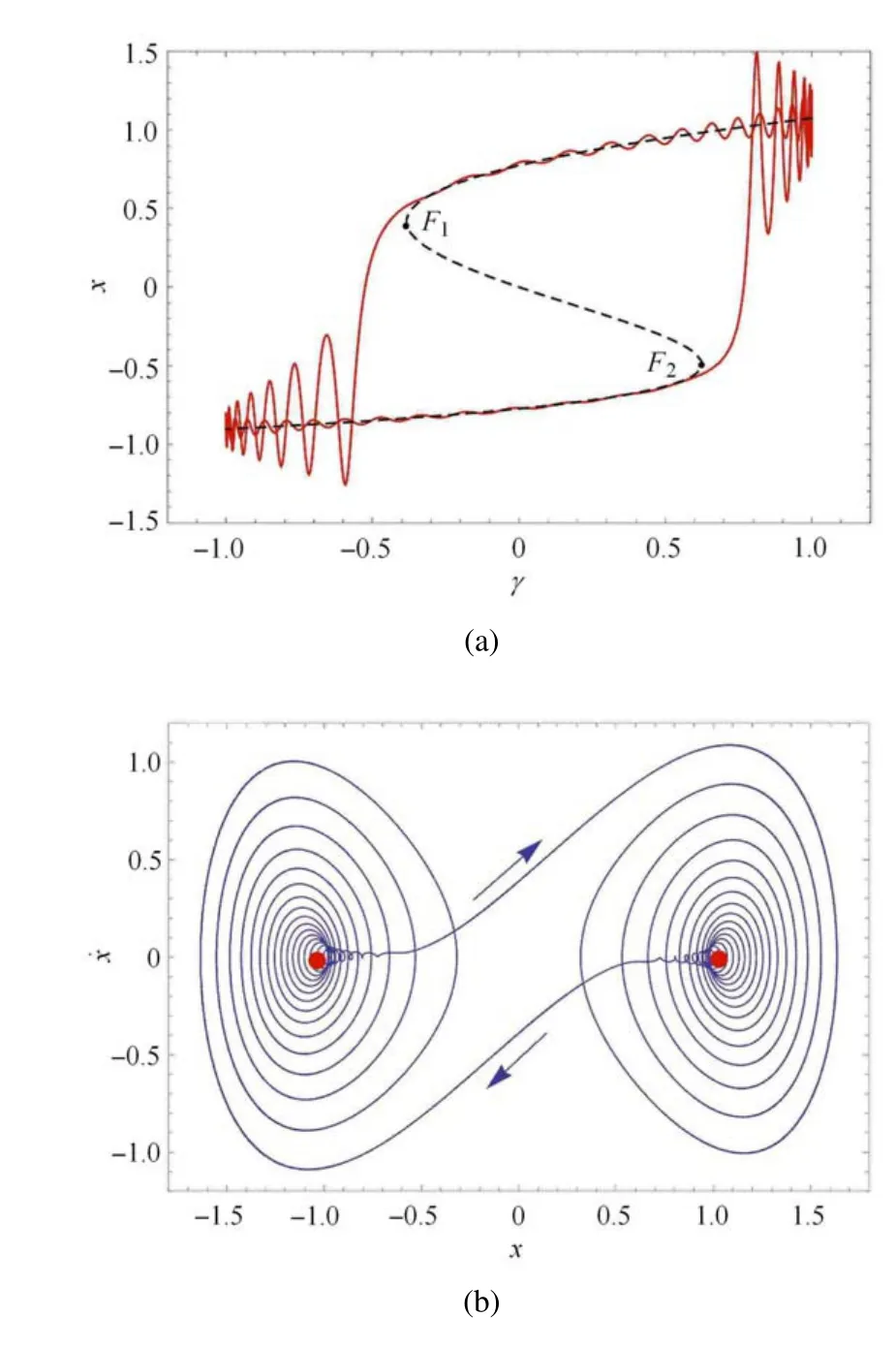
圖7 Fold/Fold簇發振蕩的疊加圖、相圖和時間歷程圖Fig.7 Composition diagram,phase diagram and time history diagram of Fold/Fold bursting

文獻[16]表示重復尖峰狀態可能圍繞F1振蕩，平衡點可能從一種狀態轉變為另一種狀態，尖峰行為可以主要由具有較小實部的相關特征值來決定.

假設系統從下分支上的某一點開始運動，它沿著S 型曲線緩慢向右側移動，直到到達折疊點，它突然從下分支跳躍到上分支，并且圍繞上平衡分支F1開始大幅振蕩，表現為S P+.隨著慢變參數的增大，振蕩逐漸減弱.直到慢變參數到達1，系統開始反向運動，然后進入弛豫振蕩狀態，最后進入靜息態，隨著慢變參數的不斷減小，系統到達另一個折疊點，并且在此時從上分支突然跳躍到下分支，開始圍繞F2進行大幅振蕩，表現為S P-.振蕩逐漸減弱，直到慢變參數到達-1，系統開始反向運動，然后進入弛豫振蕩狀態，最后進入靜息態.如此循環.這就構成了一個周期完整的Fold/Fold 簇發振蕩.

該簇發振蕩的類型可以稱為對稱周期性Fold/Fold 簇發振蕩，因為此時的系統穿過路徑曲線的位置是對稱的.

然后解釋β1,β2,a的任意性不改變系統的動力學行為.使用一條曲線路徑，軌跡的形狀如圖8(a)所示.為了方便觀察雙穩態現象，對系統進行歐拉離散，得到圖8(b).可以看出圖8(b)存在兩條分支，如果沒有Fold/Fold 簇發振蕩，離散后的分岔圖只會有一條曲線.當a=0 時，它有一個點(0,β2)始終在μ2軸的上方，而規定了β2必須大于0，這也就解釋了在0 ＜β1＜1，0 ＜β2＜1 的情況下，無論β1，β2的取值為多少，都不影響Fold/Fold 簇發振蕩產生.并且，此時的Fold/Fold 簇發振蕩是對稱的.

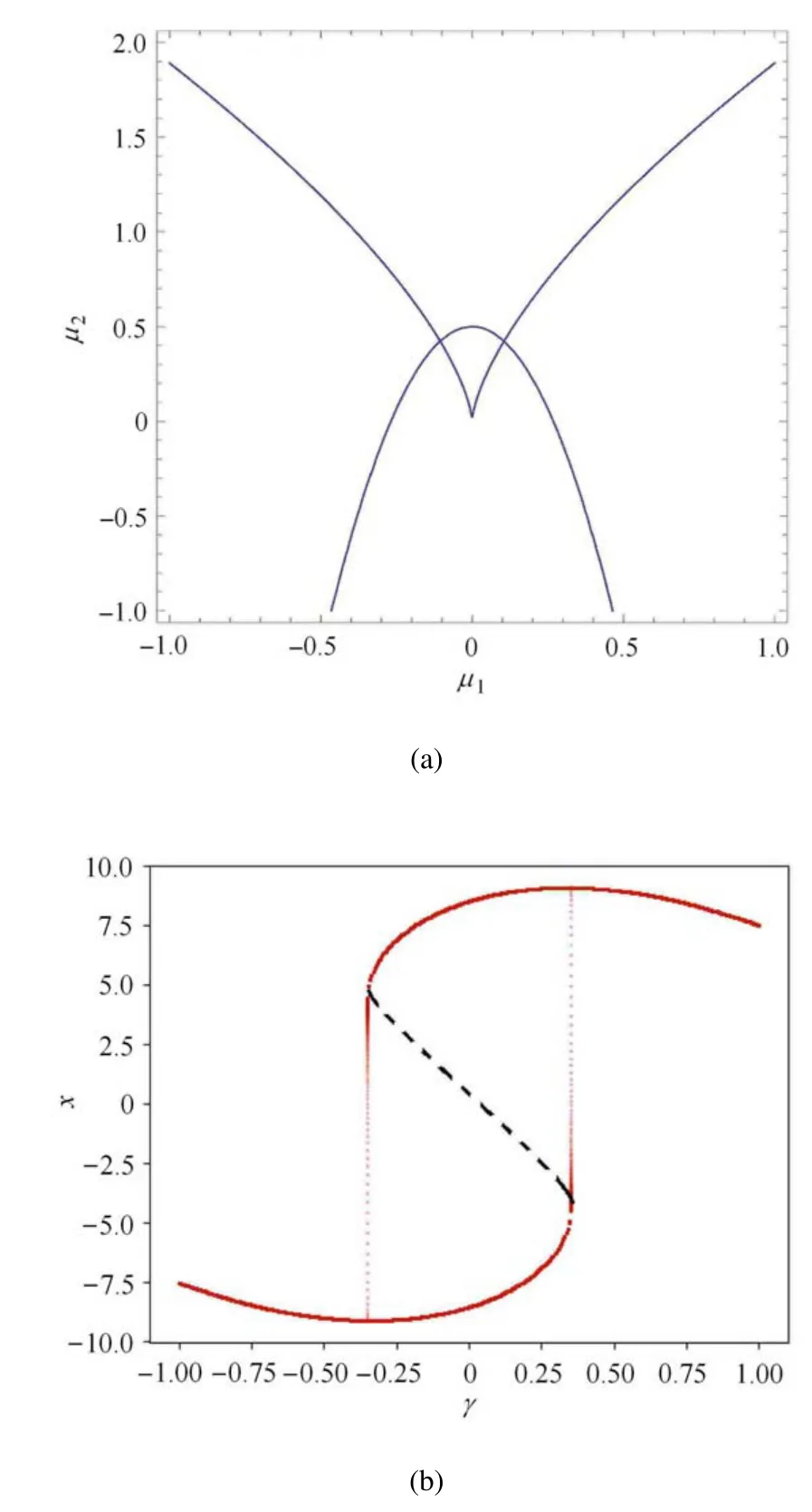
圖8 對應的路徑與離散分岔圖Fig.8 The corresponding path and dispersed bifurcation diagram

其次，考慮a的變化會帶來什么影響，此時，鞍結曲面的位置由.路徑方程變成為

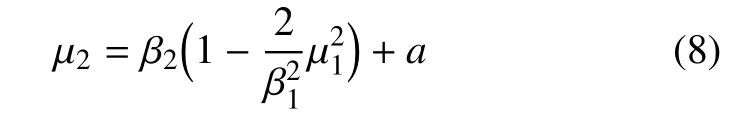
相當于原路徑向上平移了a個單位，路徑與鞍結曲面必然會相交，只需要保證是在有效范圍內相交即可.又由于任意a∈(0,1)都滿足0 ＜μ2＜1.這也解釋了無論a為何值，在上述的路徑下，這并不影響系統從一側曲面穿到另一側曲面.更多關于不同頻率比與相位差的情況，如表1 所示.

表1 β1=0.38,β2=0.34 三種情況下的分岔圖Tabel 1 Three bifurcation diagrams in case of β1=0.38,β2=0.34

3 當a ≠0 時，Fold/Fold 簇發振蕩的出現與消失

在上一部分中主要介紹了系統(2)的相關簇發振蕩，結合時間歷程圖、相位圖、疊加圖仔細地說明了系統是如何運動的.通過參數空間的展開理論和路徑說明了系統(2)發生簇發振蕩的原因，以及在不同參數下系統的不同行為.在這一部分，介紹新增的常系數項會對系統(1)的動力學行為帶來什么影響.先通過數值模擬，發現了一種現象，之后進一步揭示這一現象產生的機理.

考慮當a≠0 時對簇發振蕩產生什么影響.固定β1=0.38，ω=0.03，β2=0.80，當a從0.22 變化到0.23 時系統的動力學行為發生巨大的變化.

由圖9 可以看出在a=0.22 時，時間歷程圖表示了簇發振蕩的存在，而當a=0.23 時，時間歷程圖由原來的兩段振蕩變成了只有上部分的細微振蕩，此時簇發振蕩已經消失.使用線性路徑解釋常系數項a的出現卻會帶來Fold/Fold 簇發振蕩.

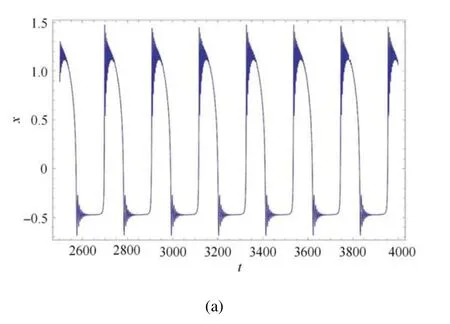
圖9 β1=0.38,ω=0.03,β2=0.80,v=0.1，系統(1)的時間歷程圖當a=0.22 時表現出簇發振蕩，當a=0.23 時簇發振蕩消失Fig.9 β1=0.38,ω=0.03,β2=0.80,v=0.1,time history diagram of system(1)showing the bursting oscillation with a=0.22 and bursting oscillations disappear with a=0.23

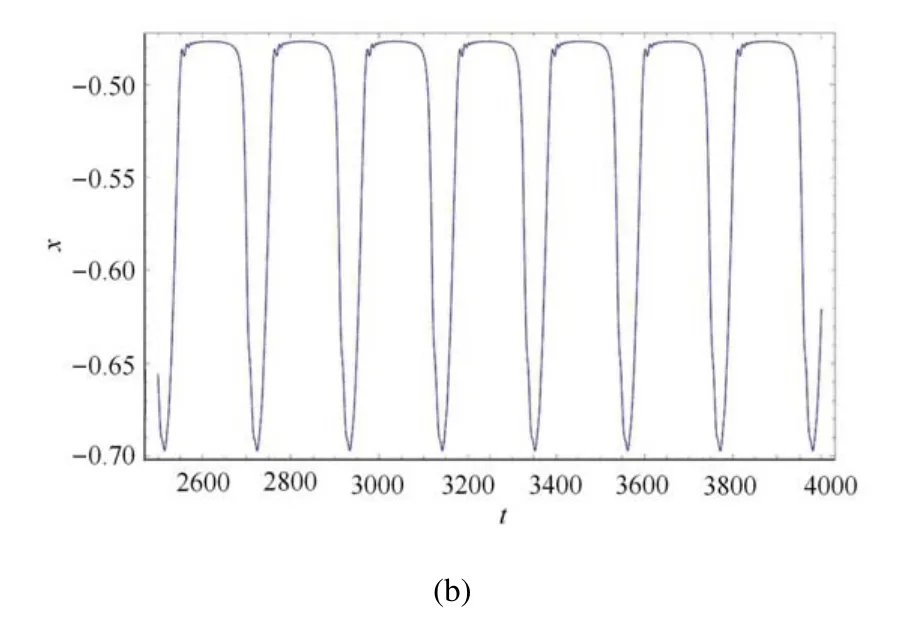
圖9 β1=0.38,ω=0.03,β2=0.80,v=0.1，系統(1)的時間歷程圖當a=0.22 時表現出簇發振蕩，當a=0.23 時簇發振蕩消失(續)Fig.9 β1=0.38,ω=0.03,β2=0.80,v=0.1,time history diagram of system(1)showing the bursting oscillation with a=0.22 and burstingoscillations disappear with a=0.23(continued)

事實上，若沒有常數項，此時路徑方程為

此時路徑表現為經過原點的線性函數，無論如何，都不會實現從一側曲面穿越到另一側曲面.若增加了常系數項，則為從一側曲面穿越到另一側曲面提供了可能的路徑，僅在二維空間角度考慮，我們有線性路徑

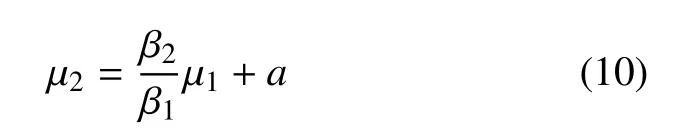
當β1=0.38,β2=0.80,a=0.22 時，路徑為μ2=2.11μ1+0.22，此時正處于臨界狀態.路徑經過鞍結曲線的一側，但與另一側相切，也就是恰好沒有經過，此時若控制a＜0.22，路徑會穿過左右兩側的曲線，可以實現不對稱的Fold/Fold 簇發振蕩.

4 多重Fold/Fold 簇發振蕩

本節將討論當μ1=β1cos(nθ)而μ2=β2cos(θ)時會產生什么現象，并且給出了不同現象背后的原因.此時系統變成如下形式

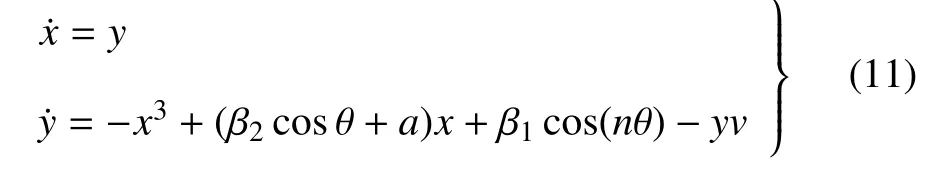
此處，令cos(nθ)=fn(cos θ)，使用結合二項式展開和de Moivre 公式，可以得到

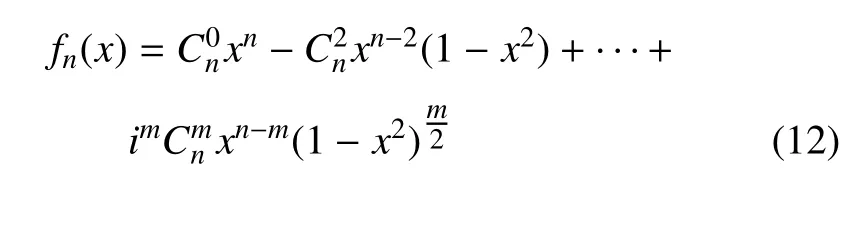
當n=3 時，代入cos(3θ)=4 cos3θ-3 cos θ，可以得到路徑方程為

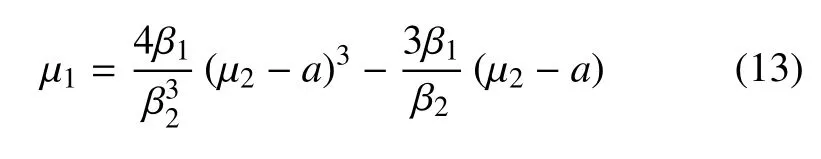
此時的路徑關于μ2=a成中心對稱.選用不同的參數可以實現該路徑與鞍結曲面交點個數的不同，該系統的動力學行為最高可以表現出三重Fold/Fold 簇發振蕩.固定β1=0.436,β2=0.327,ω=0.03，v=0.1 通過改變參數a來實現不同重數的Fold/Fold 簇發振蕩.a=0.5 的時間歷程圖、疊加圖和路徑圖如圖10 所示.

在圖10 中的時間歷程圖中，陰影部分表示一個周期內的動力學行為，黑色方框表示這個周期內發生Fold/Fold 簇發振蕩.可以很明顯看出，當a=0.5 時系統發生三次Fold/Fold 簇發振蕩.隨著a的減小，系統的“1,2,3”振蕩會出現不同程度的變化.當a=0.2 時，系統將只發生兩次Fold/Fold簇發振蕩，與a=0.5 相比，振蕩“1,2”的差別不大，但是振蕩“3”會明顯減弱.當a=-0.1 時，系統的動力學行為會再次改變，與前兩者相比，振蕩“1”的差別不大，振蕩“2”明顯減弱，而振蕩“3”幾乎不顯示振蕩行為.最后當a=-0.5 時，振蕩“1,2,3”幾乎都會消失了，此時沒有發生Fold/Fold 簇發振蕩.其中振蕩“3”消失的最為徹底，其次是振蕩“2”，振蕩“1”還殘存著微弱的振蕩.

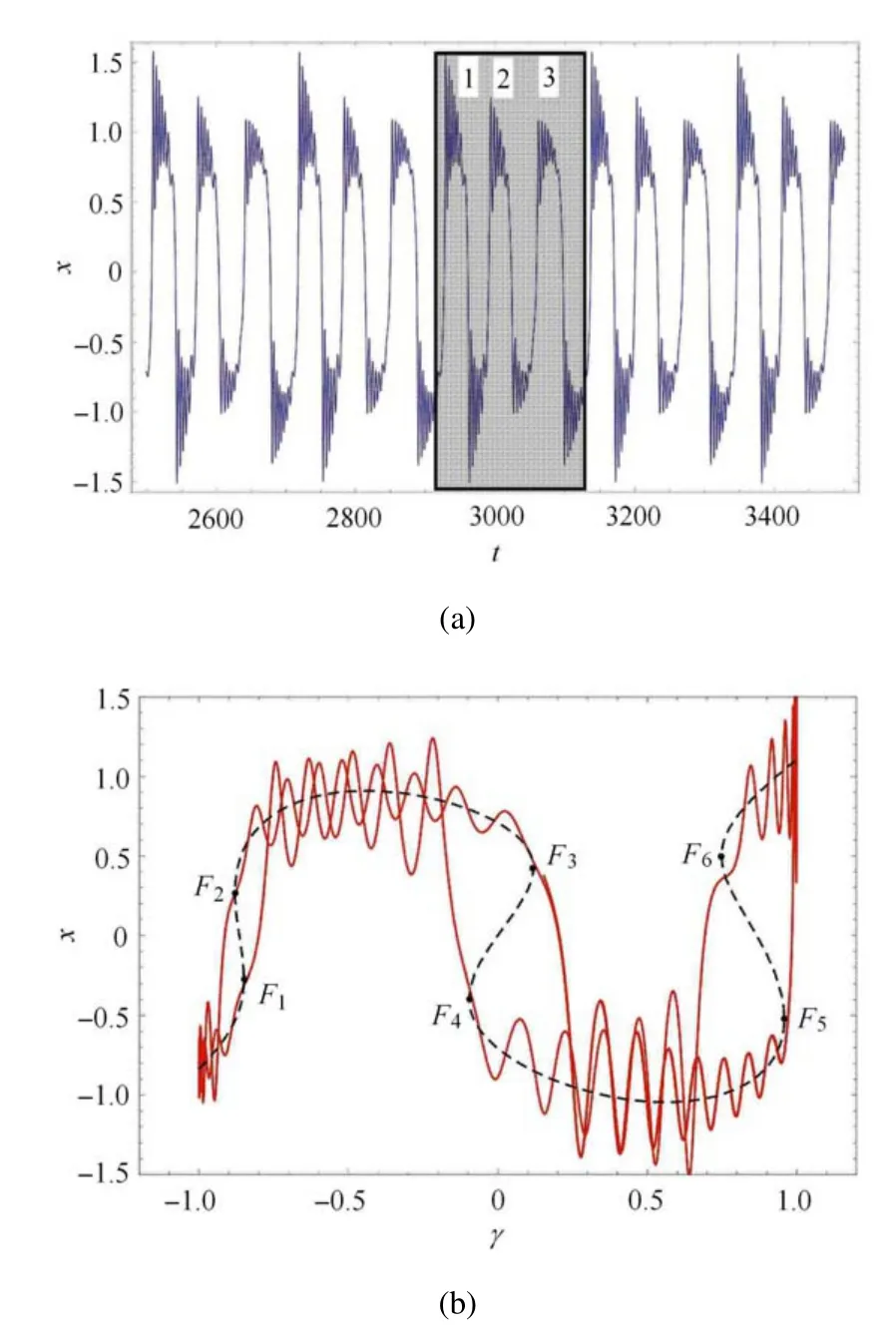
圖10 對應的時間歷程圖、疊加圖、路徑圖Fig.10 Time history diagram,composition diagram and path diagram

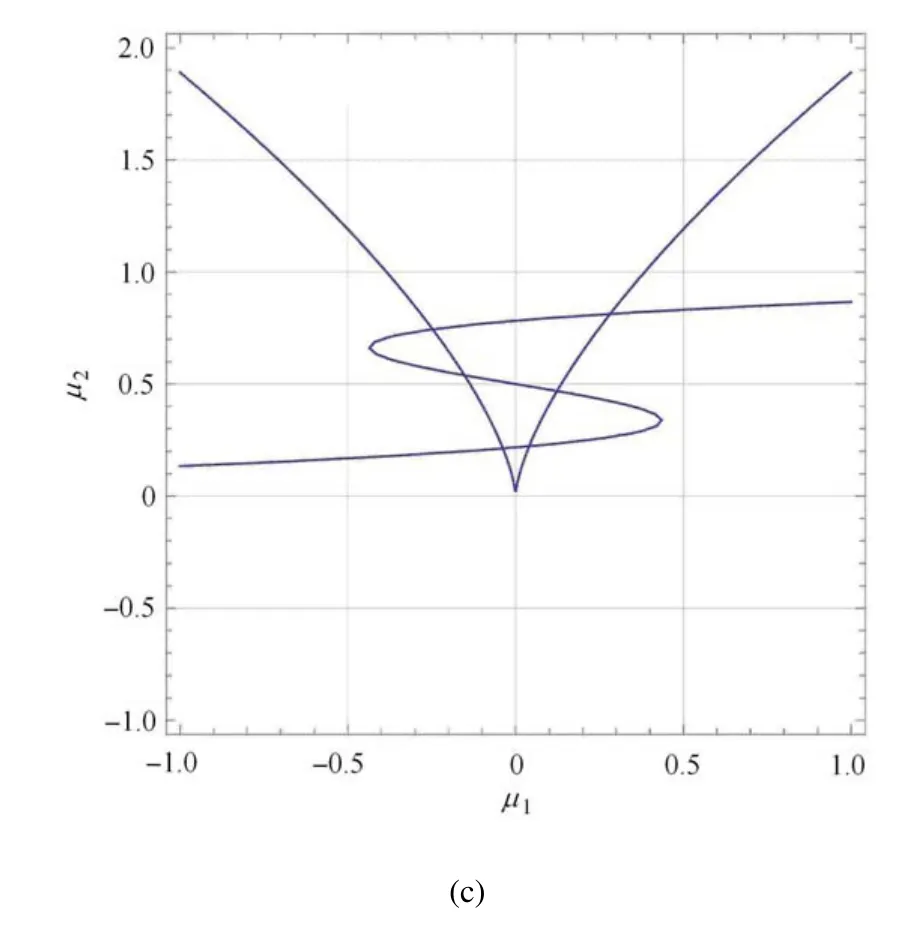
圖10 對應的時間歷程圖、疊加圖、路徑圖(續)Fig.10 Time history diagram,composition diagram and path diagram(continued)

這是由于路徑最多與鞍結曲面三次相交，即穿過鞍結曲面的兩側.一次相交就對應于一次Fold/Fold 簇發振蕩.在a=0.5 時，產生了三次相交，在a=0.2 時，產生了兩次相交；a=-0.1 時，產生了一次相交；a=-0.5 時沒有相交.

從路徑圖中可以發現路徑與曲面相交的情況復雜多樣.表2 表示了不同情況下的Fold/Fold 簇發振蕩.

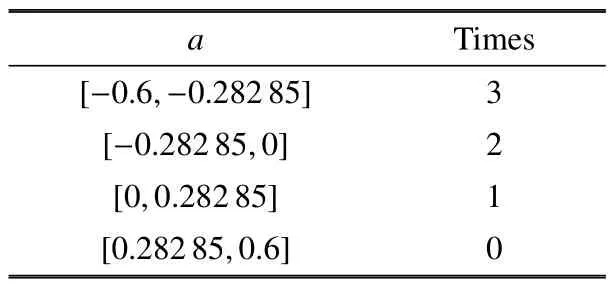
表2 Fold/Fold 簇發振蕩重數與a 的關系Tabel 2 The relationship between a and the number of Fold/Fold bursting

關注最大重數在理想的狀態下與n之間存在的聯系.以n為奇數時為例，結合二項式展開和de Moivre 公式，整理系數可以得到

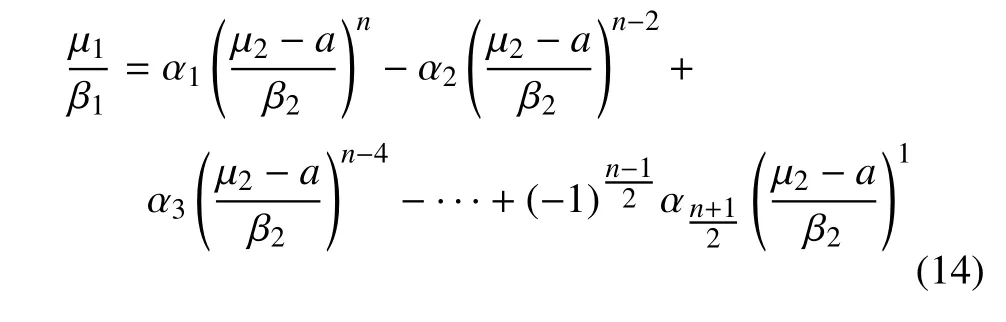
從該式的固有特點可以看出路徑都可以分割成n段，因此理想狀態下，如果能使得n段都與鞍結曲面有交點，就可以產生n重Fold/Fold 簇發振蕩.

5 結論

系統(1)是一類含有兩個慢變量的Duffing型方程，實驗研究表明其存在雙穩態現象.為了深入理解系統(1)的動力學行為，本文從數值模擬和理論分析兩個方面來討論該系統的混沌特性及簇發振蕩行為，得到的結論如下.

(a) 對于系統(2)當振幅參數取值大于1 時，系統表現出了不動點混沌.并且隨著參數的變化，不動點混沌可能表現為單支存在或者雙支合并.通過叉式分岔解釋了當慢變參數小于0 時，系統只有一個穩定解，而當慢變參數大于0 時，系統產生一對穩定的解，隨著慢變參數的繼續增大，系統出現了混沌.

(b)對于系統(1)來說，它只會產生Fold/Fold 簇發振蕩，這是由于它的參數空間中只有鞍結曲面，如果存在其它曲面，對于路徑的變化應該十分敏感.并且產生的Fold/Fold 簇發振蕩與v的取值無關.對于μ2-μ1型的路徑不論是曲線還是線性只要保證它能在有效范圍內穿過鞍結曲面的兩側，就能發生Fold/Fold 簇發振蕩現象.這能解釋第二部分中a,β2選擇時的任意性的原因；第三部分中常系數項a的變化使得系統發生巨大改變的原因.值得一提的是穿越鞍結曲面的位置還與Fold/Fold 簇發振蕩的對稱有關.更多關于不同頻率比與相位差的情況，表1 標注了它們是否會得到Fold/Fold 簇發振蕩.

(c)當μ1=β1cos(nθ)，μ2=β2cos(θ)時使用μ1-μ2路徑討論產生的現象，此時系統表現出多簇發振蕩現象.探究了不同重數的Fold/Fold 簇發振蕩與n值之間的關系.由于路徑都可以分割成n段，因此理想狀態下，n段都會與鞍結曲面有交點，從而產生n重Fold/Fold 簇發振蕩.