自抗擾控制框架下的摩擦力振動分析1)

樸敏楠 王穎 周亞靖 孫明瑋,2) 張新華 陳增強

*(南開大學人工智能學院,天津 300350)

?(空間物理重點實驗室,北京 100076)

**(北京自動化控制設備研究所,北京 100074)

引言

摩擦力廣泛存在于各種機電系統,是影響控制性能的關鍵因素[1-3].在低速運動時,摩擦力會誘發極限環振動.對于給定的控制器,準確地分析極限環振動對控制參數選取以及決定是否更改控制策略有重要的指導意義.

盡管PID 控制及其各種改進形式是運動控制中最常用的算法,其單自由度控制結構下固有的抗擾和跟蹤性能矛盾問題一直是尋求性能更佳控制器的動力.為改進傳統PID 控制,中科院系統科學研究所韓京清研究員提出了一種新的工程化控制方法—ADRC[4].該方法將串聯積分器視為系統標準型并采用擴張狀態觀測器(extended state observer,ESO)對總擾動進行實時估計.具有兩自由度控制結構的ADRC通過ESO 和誤差反饋控制律可以實現抗擾和跟蹤性能的分開設計.近些年來,ADRC 在運動控制平臺上得到了越來越多的成功應用[4-10].由于ADRC 的等效控制律中存在積分作用,在低速運動時容易產生極限環或者黏滑振動.目前,ADRC 框架下的摩擦力振動研究甚少,僅有的工作也是基于描述函數法[8-9],得出的分析結果在只有庫倫摩擦力時精度尚可,但是當考慮靜摩擦力時卻存在較大的誤差[11].

在已有文獻中,摩擦力振動分析基本都是針對PID 控制或者PD 控制,主要采用描述函數法、代數方法、相平面法和非線性動力學系統分析方法[11-20].描述函數法是一種近似方法,僅適用于分析在有限時刻速度為零的極限環,因此具有一定的局限性.針對一類僅包括靜摩擦力和庫侖摩擦力的單自由度運動系統,文獻[14] 采用精確的代數方法證明了任何可以使系統穩定的PID 控制參數組合都會產生極限環.代數方法雖然能夠提供準確的分析結果,但是由于需要計算解析解,其僅適用于低階控制系統(三階及以下)和特定的靜態摩擦力模型.針對靜態摩擦力模型,文獻[15-17]采用相平面法將三維控制系統降為一維,并通過事件對映(event map) 分析了不同摩擦力模型以及參數對平衡點集和極限環的影響.對于帶有Stribeck 效應(零速度附近的摩擦力驟降)的指數摩擦力模型,文獻[17]中結果表明Stribeck 負斜率參數會直接影響極限環解的個數、穩定性以及能否通過參數整定消除極限環.該結論可視為文獻[14]中結論的拓展,對現實中能夠通過PID 參數調節消除極限環的一些情形進行解釋.盡管事件對映是一種直觀有效的分析方法,但是由于需要將系統用一維對映來表示,其僅適用于靜態摩擦力模型,無法對包括更為復雜的動態摩擦力模型的運動控制系統進行分析.隨著計算能力的增強,針對一般非線性動力學系統的分析工具如打靶法、軌跡跟蹤(path following)、分岔圖、Floquet 理論等被弓入到閉環的摩擦力振動分析中[18-27].該方法能夠對包含一般摩擦力模型的系統進行分析.針對靜態切換摩擦力模型[21]和動態LuGre 模型[28],文獻[18]采用簡單打靶法結合軌跡跟蹤得到關于控制增益的極限環解枝軌跡.結果表明包含這兩種摩擦力模型的系統呈現出非常相似的特性,當控制增益大于某一臨界值時,極限環會消失.文獻[19-20] 聯合解析方法和數值方法,針對三階控制系統采用打靶法結合二分法在理論參數范圍內計算令極限環消失的最小積分泄漏值.文獻[22]采用分岔圖對設計狀態觀測器和摩擦力前饋補償策略的閉環系統進行極限環分析.

基于上述分析,本文研究ADRC下的極限環振動.首先,考慮兩種典型的靜態和動態摩擦力模型,設計不同階次的ADRC,并得到其等效形式以沿用PID 控制下的結論以及與PID 控制進行比較.為了準確計算高階控制系統的極限環,采用非線性動力學系統的分析工具[29-32],使用打靶法結合擬弧長延拓跟蹤關于ESO 帶寬的極限環解枝.通過計算Floquet 乘子(floquet multiplier,FM) 判斷極限環的穩定性、分岔點的出現以及類型.擬弧長延拓方法能夠克服傳統局部延拓方法不能順利通過折疊點的缺點.此外,通過雅可比矩陣和近似數值方法對兩種系統平衡點集的局部穩定性進行了分析.最后,通過仿真研究了Stribeck 負斜率參數、控制器階次、誤差反饋調節帶寬以及觀測器帶寬對極限環以及平衡點集的影響,并對比兩種摩擦力模型下的結果.所得結論可以解釋一些現實情形并對參數整定提供一定指導.

1 模型介紹與控制器設計

考慮一類二階運動系統

其中,J是轉動慣量,θ 是轉動角度,u是控制電壓,cm是輸入增益,Ff是摩擦力.現實中的摩擦力特性多種多樣,為了描述這些特性,不同復雜程度的摩擦力模型相繼被提出,主要分為靜態摩擦力模型和動態摩擦力模型.文中選用兩種經典模型,靜態切換模型[21]和動態LuGre 模型[28].切換模型可表示為

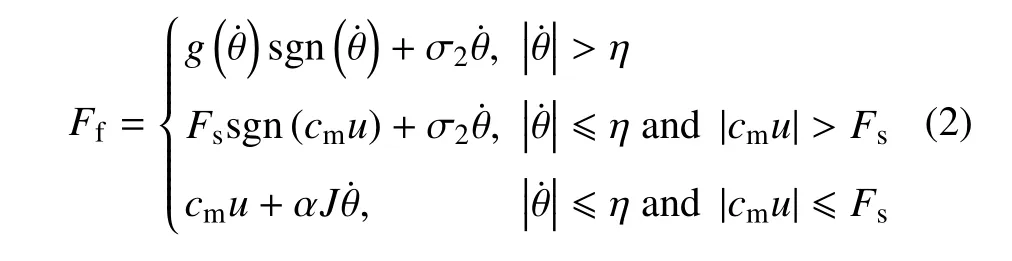
其中,η 是角速度閾值,σ2是滑動摩擦力系數,Fs是最大靜摩擦力,α 是自定義的停滯階段的加速度,的形式為

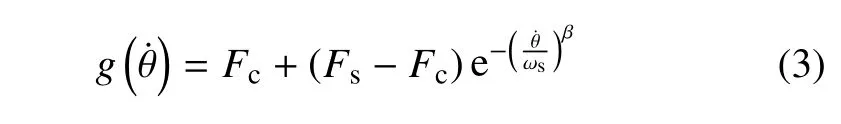
其中,Fc是庫倫摩擦力,ωs是Stribeck 角速度.該模型包括三部分,即滑動階段、由停滯切換到滑動的過渡階段以及停滯階段.通過弓入α 定義停滯狀態可以避免傳統Karnopp 模型[33]的數值不穩定問題,并且使得控制系統微分方程組變為非剛性,提高數值積分效率.Stribeck 效應指的是克服最大靜摩擦力之后摩擦力絕對值的迅速減小,是產生極限環振動的主要原因[34].β 決定了Stribeck 效應的負斜率,即摩擦力在低速時的變化速度,是影響極限環振動的關鍵參數.為了描述預滑動、滯后回線、可變最大摩擦力等現象,文獻[28]提出了LuGre 模型.該模型假設接觸面在微觀上是不規則且粗糙的,兩個剛體通過一些彈性鬃毛接觸.鬃毛的平均變形用z表示,其動態為

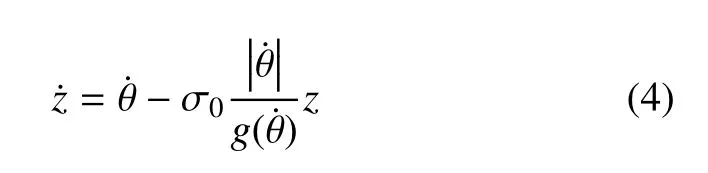
摩擦力可由鬃毛的撓曲產生,可表示為

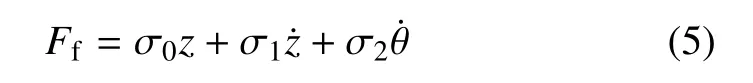
其中,σ0是鬃毛剛度,σ1是微觀阻尼系數.

現基于式(1)設計角度控制器.首先將式(1)改寫為

其中,b0=cm/J,d=-Ff/J.下面設計降階擴張狀態觀測器(reduced-order extended state observer,RESO)[36]對摩擦力進行估計.假設角度和角速度信號同時可測,則分別可以設計一階或者二階RESO.當采用角速度作為輸入時,可設計一階RESO

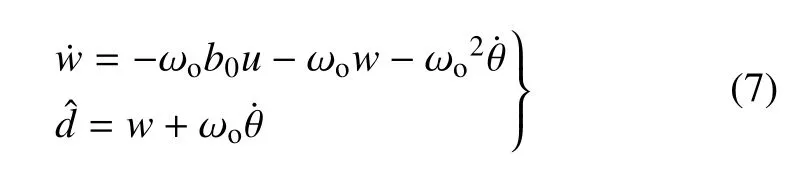
其中,w為中間狀態,ωo為觀測器帶寬,?d為摩擦力估計.得到摩擦力估計后,控制律可設計為

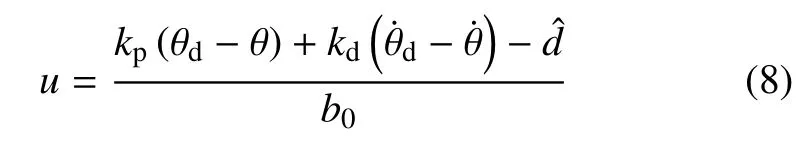
其中,θd為參考指令,kp和kd分別為比例和微分增益,為了便于分析,這里根據參數化帶寬ωc將其設計為

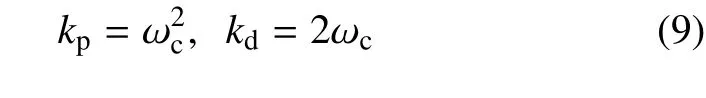
由文獻[35-36]可知,式(7)和式(8)下的等效控制律就是PID 控制,因此已有文獻中關于PID 控制在極限環振動上的結論同樣適用于針對二階對象設計一階RESO 的情形.基于文獻[14,17-18]中PID 控制下的結果,可以得到ADRC 下的幾個關鍵結論:

(1)針對只包含靜摩擦力和庫倫摩擦力的靜態模型,任何可以使系統穩定的ADRC 參數組合都會產生極限環[14].

(2)針對切換模型(2),當β ＜1 時,平衡點集是不穩定的,穩定極限環一直存在且不能通過調節ADRC參數消除(與結論(1) 吻合); 當β ＞1 時,平衡點集是局部穩定的,在一定ADRC 參數范圍內,穩定和不穩定極限環同時存在且能夠通過調節ADRC 參數消除[17].

(3)針對LuGre 模型(5),當β=2 時,極限環振動特性和切換模型下β=2 時基本一致[18].

當采用角度作為輸入時,可設計二階RESO

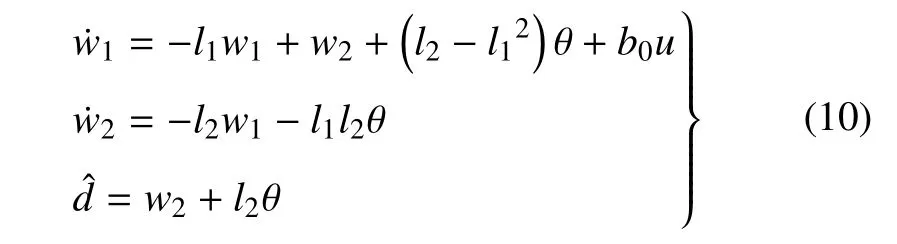
其中,w1和w2為中間狀態,l1和l2為觀測器增益,為了便于分析,這里根據參數化帶寬ωo將其設計為

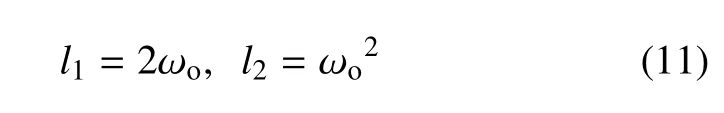
基于式(10) 可以得到RESO 對擾動估計的傳遞函數為

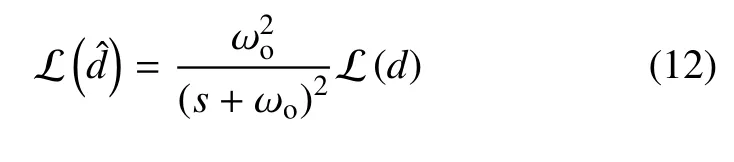
其中,L 表示拉氏變換運算符號.可以看出擾動估計的本質為擾動的低通濾波輸出.顯然,ωo越高,越能夠快速地跟蹤和補償摩擦力.因此,ωo是影響極限環振動的關鍵參數.此外,ωo的取值會受到測量噪聲、未建模高階動態等因素的限制.結合式(6)、式(8)和式(12)可以得到控制量在零初始條件時的拉氏變換為

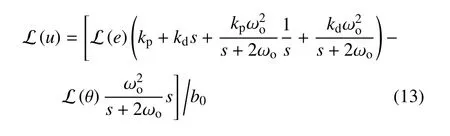
其中,e=θd-θ.可以看出ADRC 的等效控制律包括PD 控制、誤差積分濾波輸出、誤差濾波輸出和角速度濾波輸出.基于式(13),定義新的閉環系統狀態

其中,x1,x2,x3分別是誤差、誤差導數和誤差積分,x4是誤差的低通濾波輸出.相比于PID 控制,閉環系統增加了誤差濾波狀態x4,上述結論(1)～(3)可能不再適用,因此是本文的研究重點.將系統狀態重構為式(14)是為了揭示出控制器的本質以及便于將后面得到的結果與PID 控制的結果進行比較.在研究極限環振動時,不失一般性,令θd=˙θd=¨θd=0.對于切換模型,閉環系統可表示為

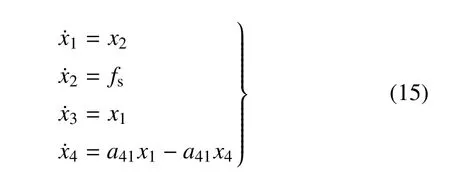
其中,切換函數fs為

其中

對于LuGre 模型,閉環系統可表示為

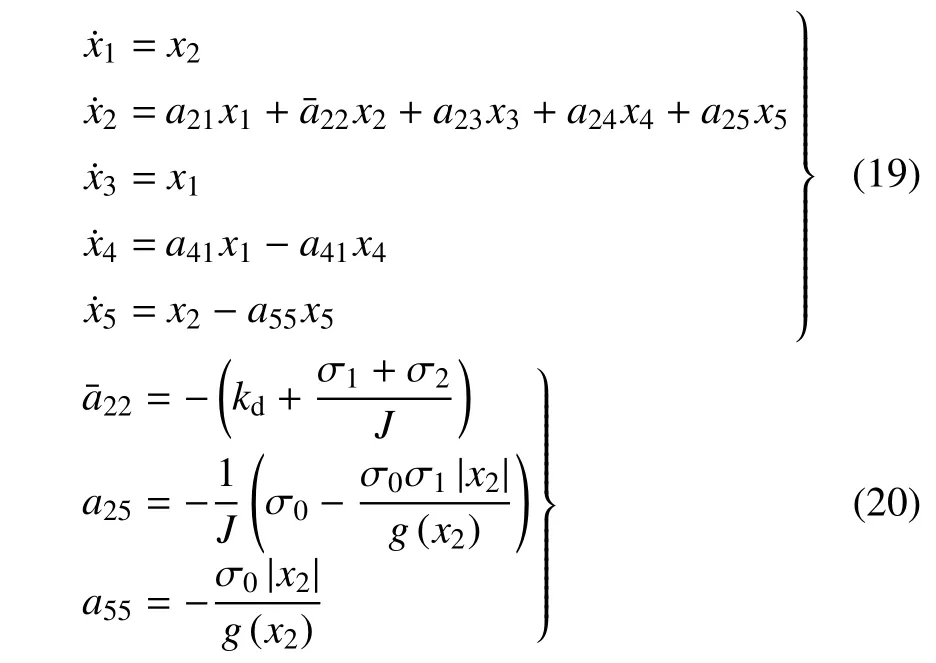
其中,x5=z.針對系統(15)和(19),本文研究控制參數ωc,ωo以及摩擦力參數β 對極限環存在性以及穩定性的影響.對于給定的控制和摩擦力參數,問題的關鍵即為準確地求解出自治系統(15)和(19)的全部周期解.

2 系統周期解計算與分析

對于系統(15)和(19),極限環的計算和分析方法相同,該部分僅針對系統(15)進行介紹.系統(15)是自治系統,即等式右端的向量場不與時間t顯式有關,不失一般性,起始時間可設為0.假設φt(x0,λ)為系統(15) 在初始條件x0=[x1(0)x2(0)x3(0)x4(0)]T下的解,其中,λ 為某個參數變量.求解極限環即為求解一個兩點邊值問題

其中

則ci可由下式解出

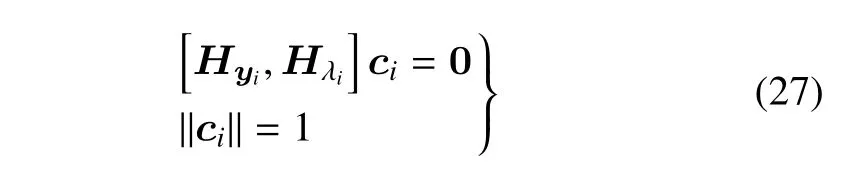
基于式(21)可得

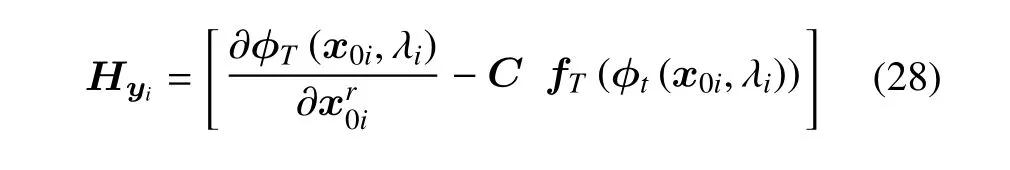
其中,帶下標i的變量表示解枝上第i個點對應的值,

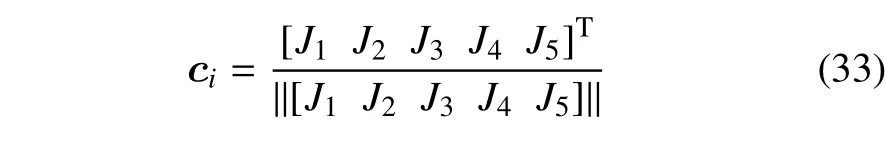
現采用牛頓迭代法對式(25)進行求解

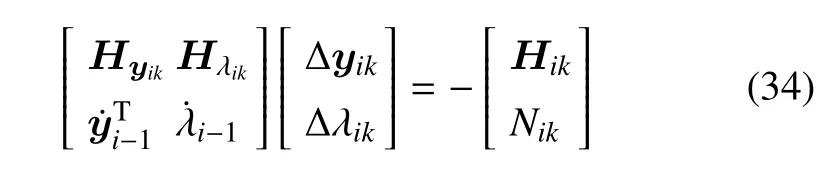
其中,下標k(k=1,2,···)表示迭代次數

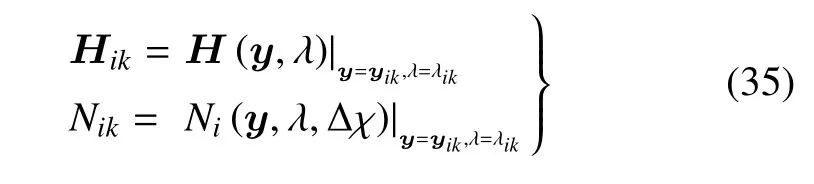
則待求解變量的迭代公式為

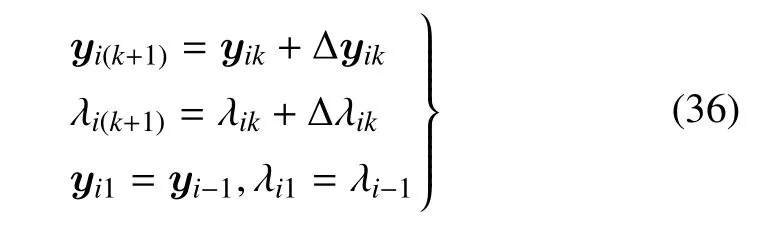
在每次迭代中,都需要多次在不同初始狀態和控制參數下進行仿真,即將一個兩點邊值問題轉化為多次的初值問題求解,這就是打靶法的思想.重復上述迭代過程直至滿足終止條件

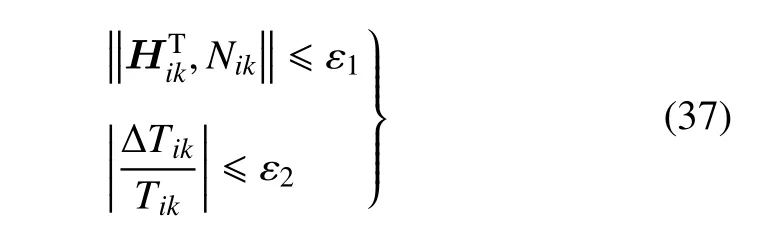
其中,ε1＞0 和ε2＞0 為充分小的值以保證求解精度.傳統局部延拓法在折疊點處存在奇異問題,無法通過折疊點繼續跟蹤解枝.擬弧長延拓法通過弓入擬弧長變量,可以避免奇異問題從而順利通過折疊點.當y為一維時,該方法的簡化原理圖如圖1 所示.

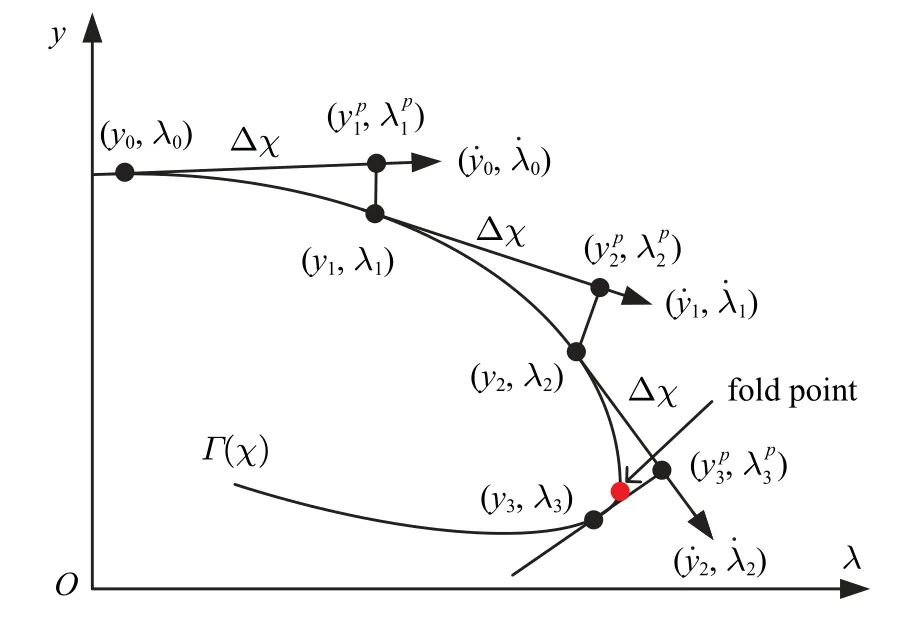
圖1 擬弧長延拓方法原理Fig.1 Principle of pseudo arc-length continuation method

極限環的穩定性以及解枝可能出現的分岔由單值矩陣的特征值FM 判斷.當所有FM 位于單位圓內時,極限環是穩定的.隨著控制參數連續變化,當某個FM 的模變為大于1 時,系統將出現動態分岔,穩定周期解被破壞[38-40].根據FM 變化情況的不同,可能出現3 種分岔:環面折疊分岔(cyclic fold bifurcation,CFB)、倍周期分岔(period doubling bifurcation,PDB)和環面分岔(torus bifurcation,TB).具體來說,當有一個FM 沿著實軸從(1,0)穿出單位圓時,將出現CFB;當有一個FM 沿著實軸從(-1,0)穿出單位圓時,將出現PDB;當有一對共軛的FM 穿出單位圓時,將出現TB.

3 平衡點集與局部穩定性

該部分首先介紹LuGre 模型下的平衡點集以及穩定性判定.由LuGre 模型性質可知[16],|z(t)| ≤Fs/σ0.因此,系統(19)的平衡點集為

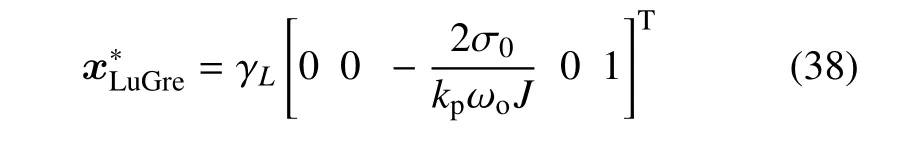
其中,|γL| ≤Fs/σ0.誤差、誤差導數以及誤差濾波輸出在平衡點處都為零,鬃毛變形產生的摩擦力由積分作用產生的控制力完全補償.平衡點集的局部穩定性可通過計算雅克比矩陣的特征值確定.由于Lu-Gre 模型是非光滑的,在求解雅可比矩陣時需要使用廣義微分[41].向量場f(x)在點x處的廣義微分定義為包含左導數f′-和右導數f′+的最小閉凸包

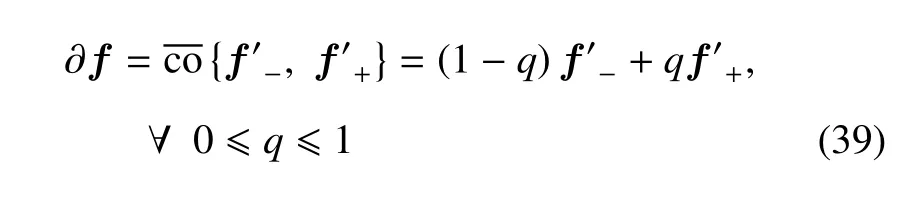
根據式(39)可以得到系統(19)在處的雅可比矩陣為

其中,I5×5為五階單位矩陣,各系數為

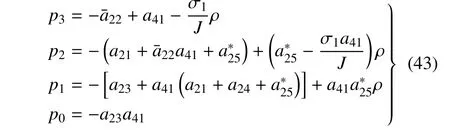
當ωc＞0 且ωo＞0 時,可以得到全部系數為正.根據Hurwitz 判據,平衡點集穩定的充要條件為

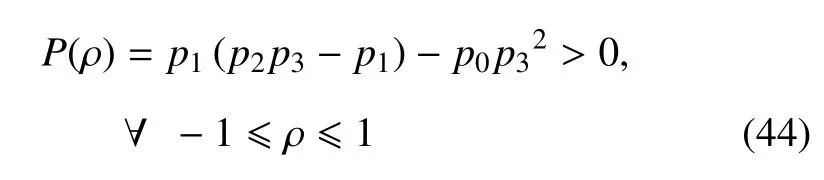
其中,P(ρ)是關于ρ 的三次多項式,因此,只需要計算P(ρ=-1)、P(ρ=1)和極小值就可以判斷式(44)是否成立.

按照切換模型的定義,系統(15)的平衡點集為

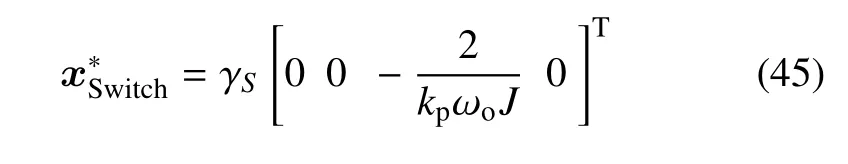
其中,|γS| ≤Fs.由于系統(15) 是Filippov 型不連續的,無法采用雅可比矩陣判斷平衡點集的穩定性.和連續微分方程組相比,判斷不連續微分方程組平衡點集穩定性的理論和方法尚不完善,已有方法大多是通過構建非常復雜的非光滑Lyapunov 函數[42-43].考慮到不是本文的研究重點,這里采用一種近似的數值方法.通過大量仿真,發現x1對解軌跡影響最為顯著.因此,對某個平衡點進行x1方向的攝動,在(0,xs)(xs為相應參數下穩定極限環的幅值)區間內選擇n個值作為攝動值,在每個攝動值下進行仿真并觀察狀態能否最終收斂到平衡點集.對于存在攝動值使得仿真結果收斂到平衡點集的情況,即可判斷此時平衡點集是局部穩定的,而且這個分析結果是準確的.對于所有攝動值下仿真結果都不會收斂到平衡點集的情況,即可判斷此時平衡點集是不穩定的,但是這個分析結果是近似的,因為初始條件沒有遍歷整個狀態空間.

4 計算結果

仿真模型參數為[18]

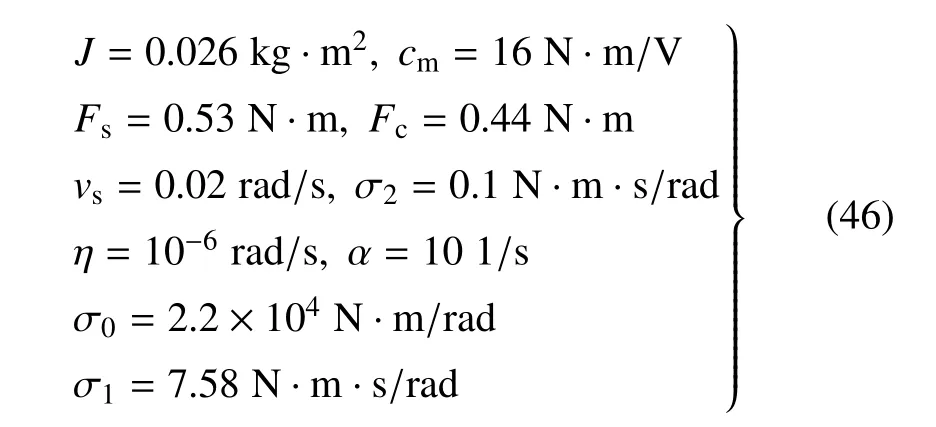
求解器選用ode45 算法,相對和絕對容許誤差限設置為10-10(需小于切換模型的角速度閾值η).參數攝動量ξ 取為初始狀態或控制參數的1%,且絕對值不小于10-8以避免數值敏感問題.Δχ 分段進行取值,當跟蹤穩定解枝時,取為2,當某個FM 的模接近1 時,減小Δχ 至0.01 以順利經過比較尖銳的折疊點.迭代精度參數設計為ε1=10-6,ε2=10-4.

4.1 基于二階ESO 和切換模型的計算結果

圖2 β=2 時切換模型系統分岔圖(實線:穩定解枝,虛線:不穩定解枝)Fig.2 Bifurcation diagram for the switch model system with β=2(solid line:stable branch,dashed line:unstable branch)

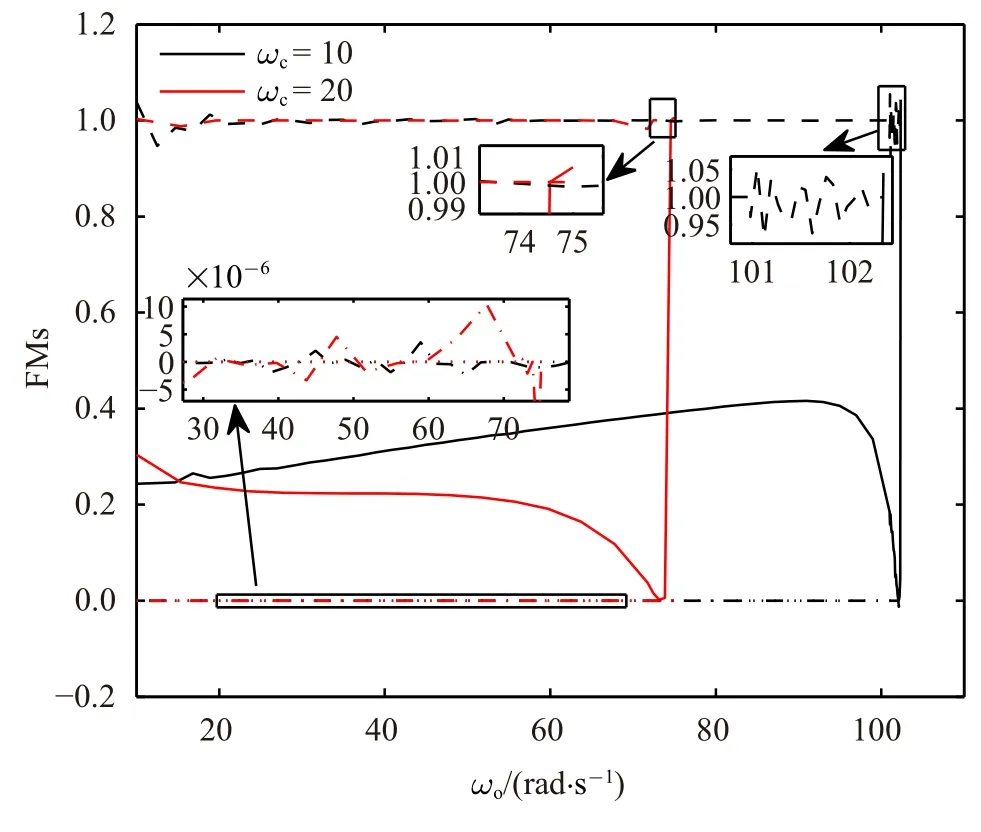
圖3 β=2 時切換模型系統穩定解枝的FMs(實線:FM1,虛線:FM2,點線:FM3,點劃線:FM4)Fig.3 FMs of stable branch for the switch model system with β=2(solid line:FM1,dashed line:FM2,dotted line:FM3,dot dash line:FM4)

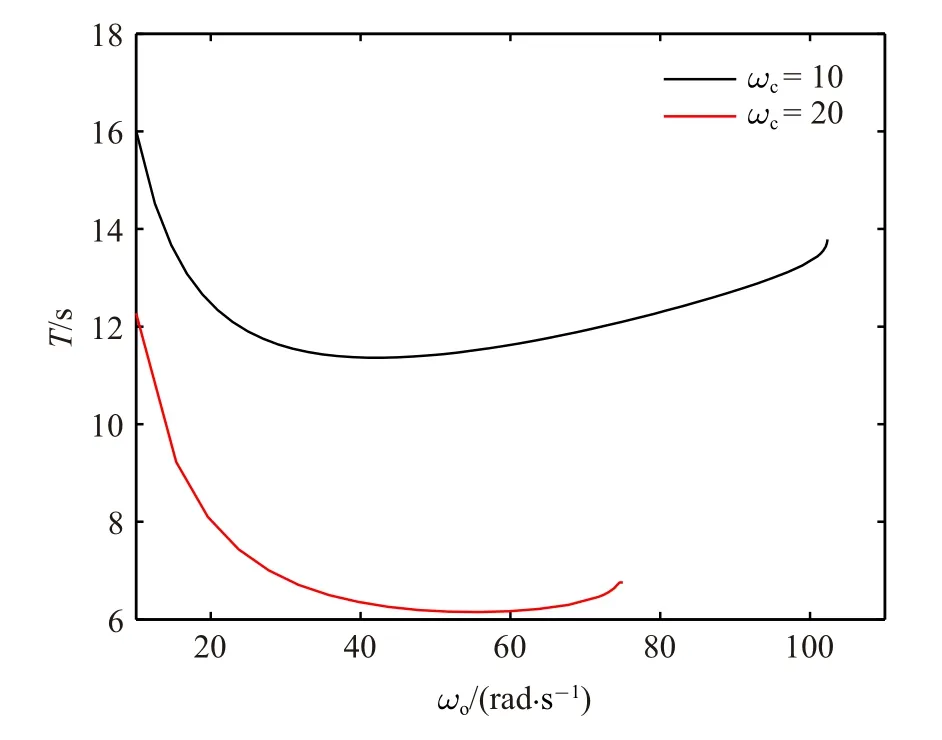
圖4 β=2 時切換模型系統的穩定極限環周期Fig.4 Period of stable limit cycle for the switch model system with β=2

首先令β=2.ωc=10 rad/s 和ωc=20 rad/s 時的分岔圖、FMs、極限環周期如圖2～圖4 所示.在以下分岔圖中,同時描述了周期解和平衡點集(x1=0),實線表示周期解或者平衡點集是局部穩定的,而虛線則表示周期解或者平衡點集是不穩定的.由于極限環可能是非對稱的,在圖2 中,max(x1)表示一個極限環周期內角度的最大值(以下簡稱為極限環幅值).在解枝起始點,ωo=10 rad/s,相應的極限環是穩定的.隨著ωo的增大,極限環幅值不斷減小.當ωo增大到某個臨界值時,有FM 沿實軸從(1,0)穿出單位圓,出現CFB,并通過CFB 產生不穩定解枝,此時對應的ωo稱為.需要說明的是,任意微小的擾動都會使得不穩定極限環的軌跡不能夠保持,不穩定極限環在現實情形中幾乎不可能出現.因此,其求解只具有理論意義,不具有實際意義.由于不穩定極限環求解計算量很大,這里只計算出了不穩定解枝的一部分,但不影響結論.當ωo＜時,系統中存在兩個相近的穩定和不穩定周期解;當ωo=時,兩個周期解匯聚一起;當ωo＞時,系統中極限環消失.對平衡點進行x1方向上的攝動,攝動值為(0,xs) 區間內均勻選取的1000 個點.通過大量仿真發現,當|x1(0)| ＜|xu|(xu為相應參數下不穩定極限環的幅值)時,軌跡會趨于系統平衡點集; 當|xu| ＜|x1(0)| ＜|xs|時,軌跡會趨于穩定極限環.所以平衡點集在所選參數范圍內是局部穩定的,且在x1方向的吸弓域近似為|x1|＜|xu|.此外,從圖2 可以看出,ωc越大,相同ωo下的極限環幅值越小,對應的也越小.FMs 如圖3 所示,其中FM1隨ωo變化明顯,FM2始終接近于1,FM3和FM4一直接近于0.FM1在CFB 附近先是驟減然后突然穿越1.FM2在1 附近的波動可認為是由數值計算誤差造成的,不能夠用于判斷是否出現分岔,因為其變化范圍很小且趨勢性不明顯.上述結果和文獻[18] 中PID 控制器下的結果很相似,只是多了一個始終接近于0 的FM.穩定極限環的周期如圖4 所示,可見周期變化非單調,呈現先減后增的趨勢,且ωc越大,周期越小.

圖5 β=0.9 時切換模型系統分岔圖(實線:穩定解枝,虛線:不穩定解枝)Fig.5 Bifurcation diagram for the switch model system with β=0.9(solid line:stable branch,dashed line:unstable branch)

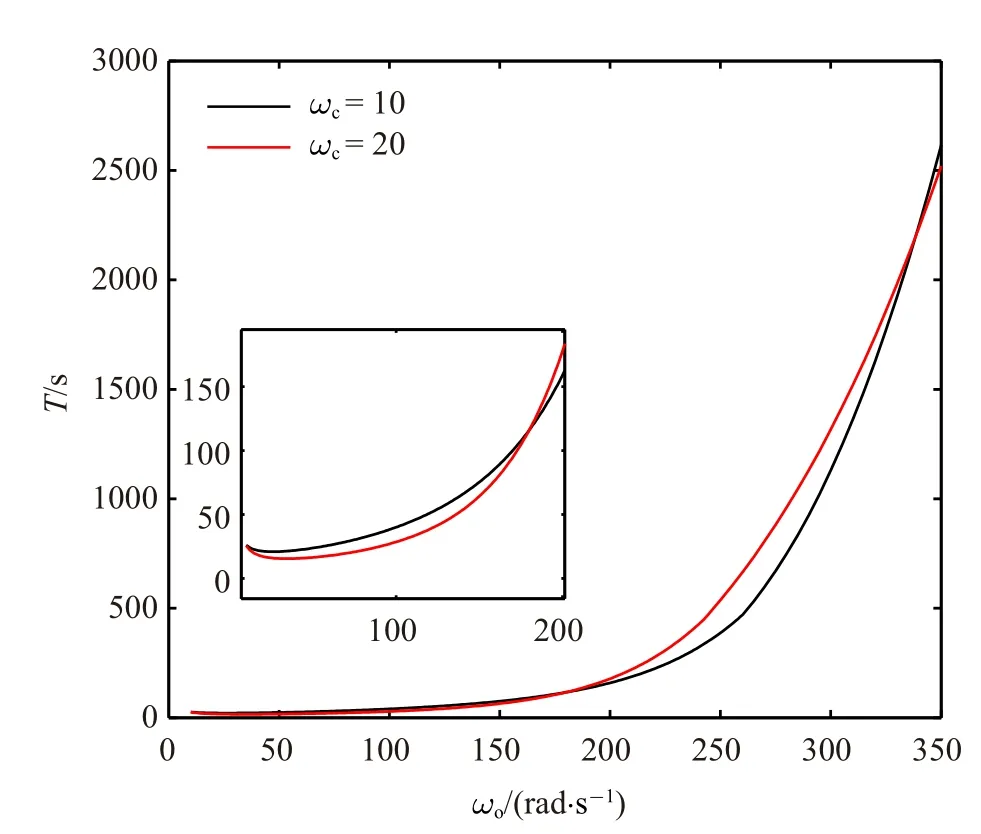
圖6 β=0.9 時切換模型系統的穩定極限環周期Fig.6 Period of stable limit cycle for the switch model system with β=0.9

為研究摩擦力參數對極限環的影響,令β=0.9.對于切換模型,β 越小,由停滯切換到滑動狀態時,在|x2| ＜ωs速度范圍內獲得的角加速度就越大,越容易產生超調,從而越容易誘發極限環.β=0.9 時的分岔圖和周期圖如圖5 和圖6 所示.當極限環幅值接近于零時,由于計算量過大終止計算.同樣,從ωo=10 rad/s 開始跟蹤穩定的極限環解枝.隨著ωo增大,極限環幅值不斷減小,周期呈現先減后增趨勢.在計算的參數范圍內沒有出現動態分岔.相比于β=2 時結果,β=0.9 時的極限環幅值更大且更加難以消除,即使觀測器帶寬很高時,仍不能夠徹底消除極限環.需要說明的是,當極限環幅值非常小且周期非常長時,極限環解雖然存在但是在某些實際應用背景下不會影響控制性能.對平衡點進行x1方向上的攝動,ωo=10,n=1000 時,ωc=10 和ωc=20 條件下能夠仿真到的最小初始角度xm分別是1.06 × 10-5(xm=xs/1000,xs=1.06 × 10-2) 和3.36×10-6(xm=xs/1000,xs=3.36×10-3),此時仍有極限環產生,可近似地認為平衡點集是不穩定的.令n取為更小值也是可以的,這樣能夠使得初始角度進一步在小于1.06×10-5和3.36×10-6范圍內進行嘗試,但是會存在以下幾個問題.首先,當初始角度非常小時,仿真時間會非常長,計算結果也會受到數值計算精度的影響.其次,即使角度間隔取得非常小,穩定性分析結果仍然可能不是準確的,因為初始狀態攝動還是只考慮了第一個狀態,沒有遍歷整個狀態空間.所以,文中令n=1000 即可滿足要求.在每個ωo下,最小初始角度攝動下的軌跡都會趨于穩定極限環,所以可以近似判斷平衡點集在所選參數范圍內是不穩定的.當ωc=10 rad/s 和ωo=30 rad/s 時,β=2 和β=0.9 下的時域仿真結果如圖7 所示.可以看出,β=2 時的周期解滿足x1(t)=-x1(t+T/2),而當β=0.9 時,這種對稱性被破壞.因此,可以推斷隨著β 的減小周期解會出現對稱破缺性分岔(symmetry breaking bifurcation,SBB)[23].

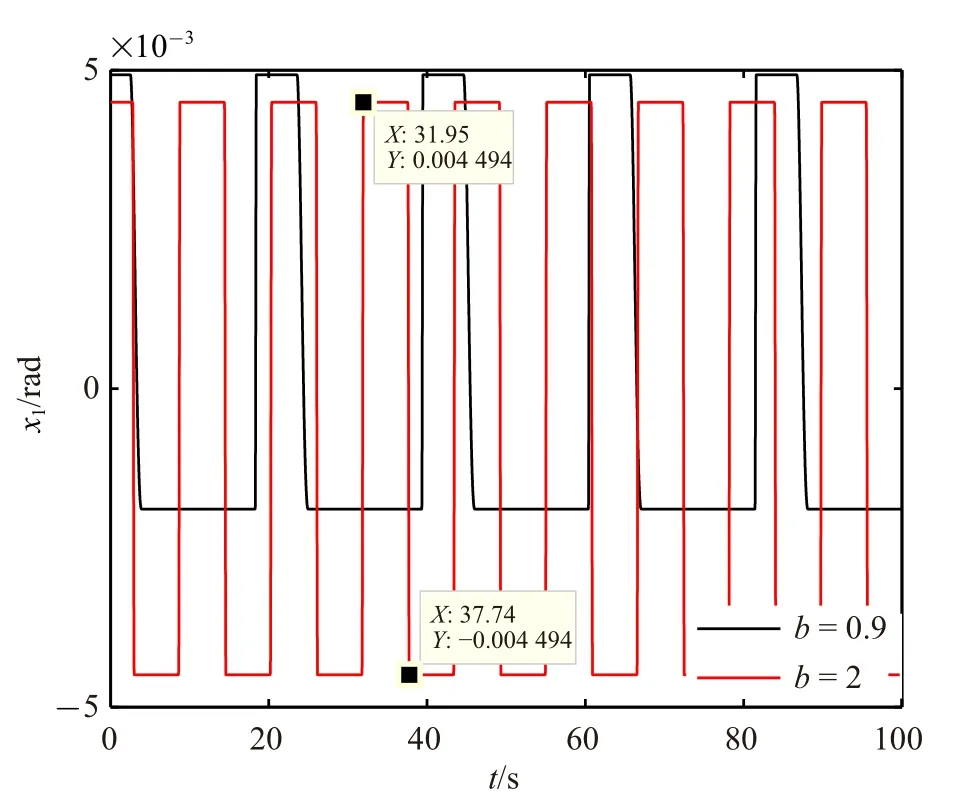
圖7 β=0.9,2 時切換模型系統的角度極限環Fig.7 Angular position limit cycle for the switch model system with β=0.9,2

4.2 基于二階ESO 和LuGre 模型的計算結果

為研究動態和靜態摩擦力模型對極限環振動的影響,采用LuGre 模型重復上述過程.當β=2 時,仿真結果如圖8～圖10 所示.和切換模型在β=2 時的結果相似,隨著ωo的增大,有FM 沿實軸從(1,0)穿出單位圓,出現CFB,并通過CFB 產生不穩定解枝.極限環幅值和周期與切換模型下的結果比較接近,稍小于切換模型對應的新增加的一個FM 在0 附近波動.β=0.9 時的分岔圖如圖11 所示.可見系統中依然出現了CFB,且比β=2時的更小,這一點和切換模型正好是相反的.對于切換模型,β 的減小增大了摩擦力的補償難度,即使ωo取值非常大也不能夠消除極限環.然而對于Lu-Gre 模型,β 的減小反而降低了摩擦力的補償難度.可以看出β 在靜態和動態摩擦力模型中有著不同的影響.按照前述方法驗證平衡點集的穩定性,可以得到所有考慮參數范圍內的平衡點集都是局部穩定的.

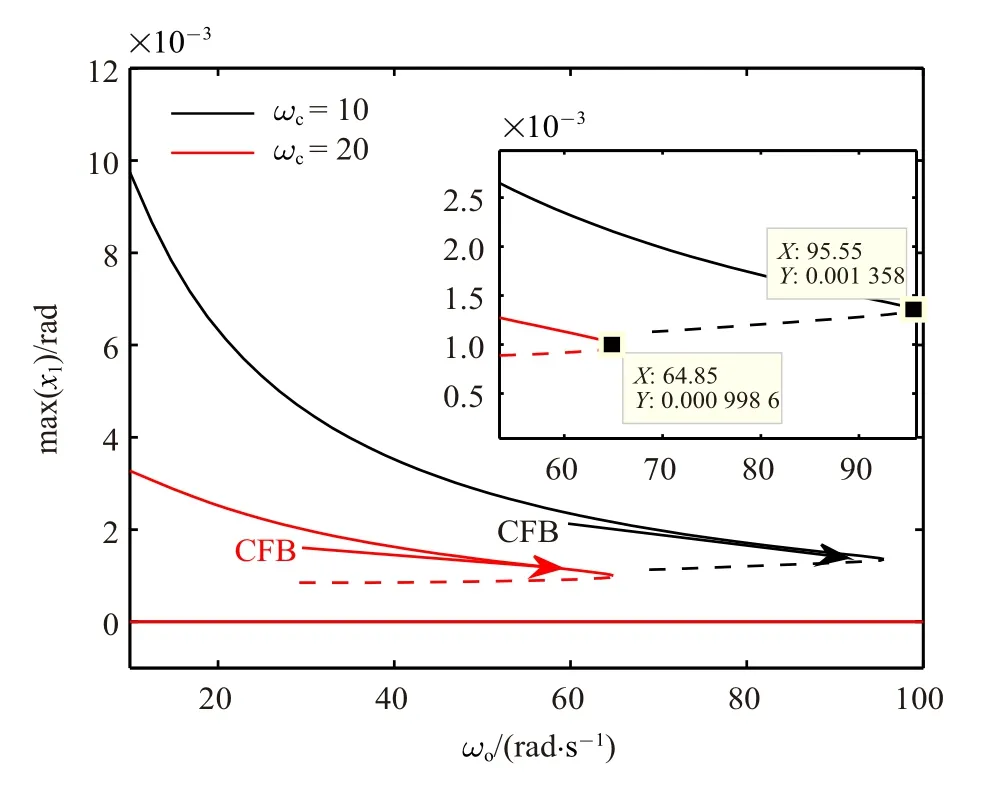
圖8 β=2 時LuGre 模型系統分岔圖(實線:穩定解枝,虛線:不穩定解枝)Fig.8 Bifurcation diagram for the LuGre model system with β=2(solid line:stable branch,dashed line:unstable branch)

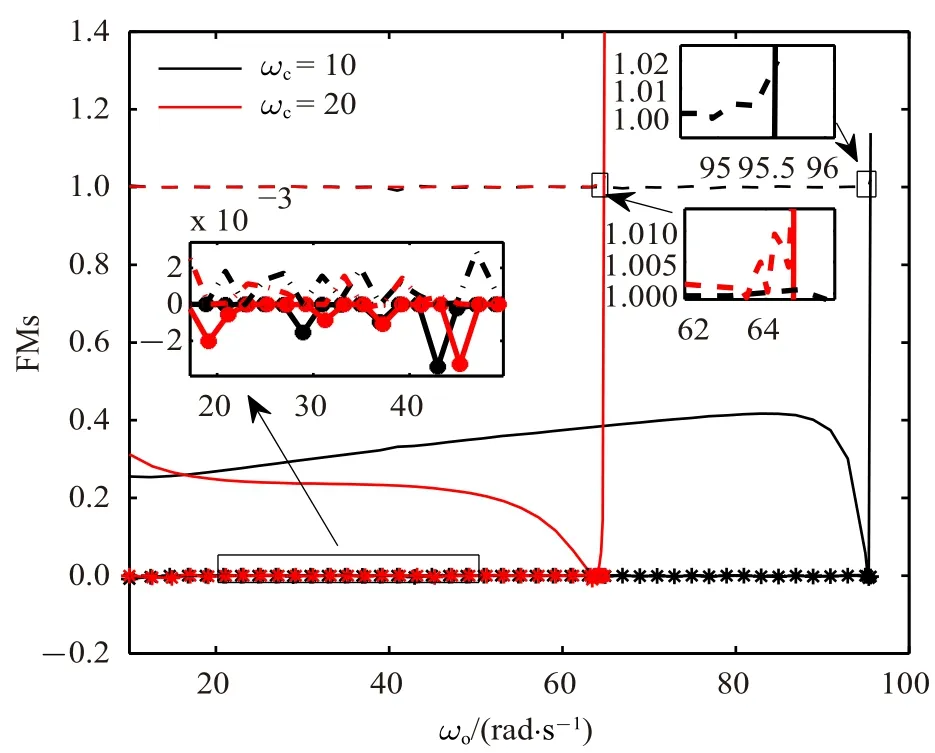
圖9 β=2 時LuGre 模型系統穩定解枝的FMs(實線:FM1,虛線:FM2,點線:FM3,點劃線:FM4,星實線:FM5)Fig.9 FMs of stable branch for the LuGre model system with β=2(solid line:FM1,dashed line:FM2,dotted line:FM3,dot dash line:FM4,solid line with star:FM5)

4.3 基于三階ESO 的計算結果

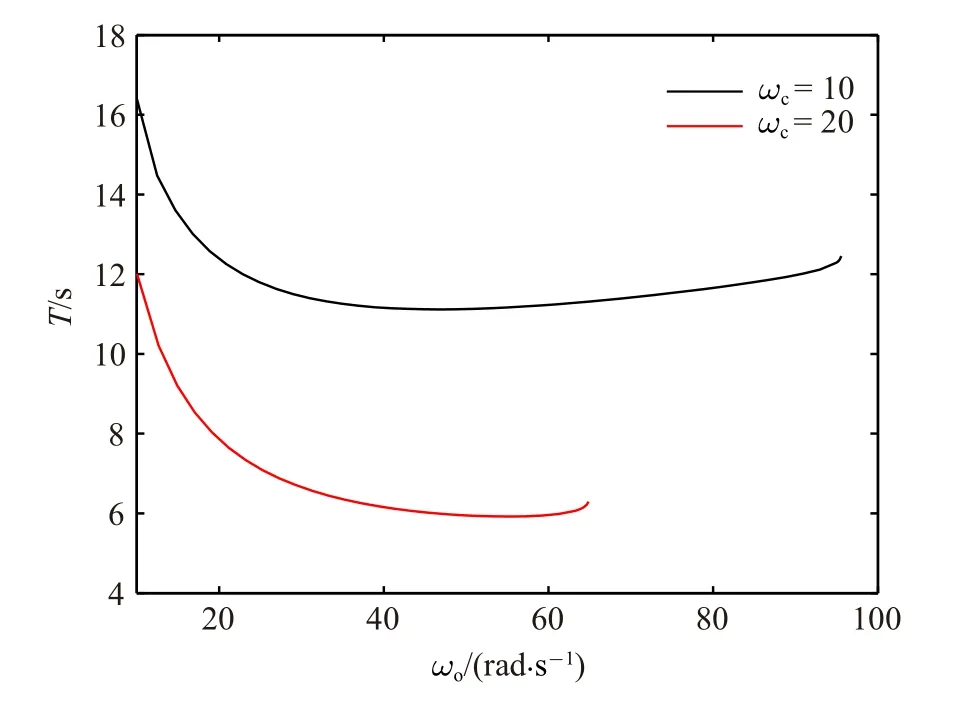
圖10 β=2 時LuGre 模型系統的穩定極限環周期Fig.10 Period of stable limit cycle for the LuGre model system with β=2

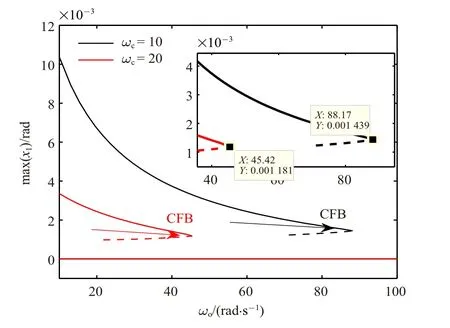
圖11 β=0.9 時LuGre 模型系統分岔圖(實線:穩定解枝,虛線:不穩定解枝)Fig.11 Bifurcation diagram for the LuGre model system with β=0.9(solid line:stable branch,dashed line:unstable branch)

上述計算結果是針對二階ESO 的,本文同樣針對全階ESO(三階ESO)重復進行了4.1 和4.2 小節中的所有計算.計算結果表明,上述所得結論(摩擦力模型、參數、ADRC 參數對平衡點集以及周期解影響) 對于三階ESO 仍然是成立的.由于閉環系統階次升高一階,切換模型系統和LuGre 模型系統分別多了乘子FM5和FM6,這兩個乘子對應的是新增系統狀態位置濾波的一階導數,且都為接近于零的數.由于篇幅限制且所得結論是相同的,該部分結果沒有在文中具體呈現.

4.4 二階三階ESO 性能對比

對于給定的摩擦力模型,降階和全階ESO 在極限環的存在性和穩定性、平衡點集的穩定性上面的結論是相同的.但是,二者在使用時效果還是存在一些區別.例如,在相同的ωc和ωo下,全階ESO 相比于降階ESO 的相位延遲更大,摩擦力補償效果更差,極限環的幅值更大.為了取得和降階ESO 相似的性能,全階ESO 的ωo應該更大以補償高階次帶來的延遲.因此,在相同的ωc下,全階ESO 對應的B更大.為了公平地對兩者進行性能對比,我們考慮兩種閉環系統在其對應的下的魯棒性能,即令摩擦力補償效果相同,比較閉環魯棒性能,研究哪一種階次的觀測器能夠更好地解決抗擾性能和魯棒性能之間的矛盾問題.我們將各種情形下的穩定裕度指標列在表1 中.其中,ESO2和ESO3分別表示降階和全階ESO,GM,PM,TM 分別代表幅值裕度、相位裕度和時延裕度.由于摩擦力模型是非線性的,在計算穩定裕度時僅考慮了滑動摩擦力,沒有考慮零速附近的摩擦力非線性.由表1 可以看出,兩個閉環系統的魯棒性能比較相近,但是ESO2下的穩定裕度尤其是相位裕度指標更好一些.因此,在設計ESO 時可以優先選擇降階ESO.

對于切換模型,當β=2,ωc=10 時,ESO2和ESO3的分別為102.3 rad/s 和158.0 rad/s,此時兩個ESO 的估計誤差傳函(L(d-?d)/L(d))的頻率響應如圖12 所示.可見,兩個ESO 的頻率響應十分接近,因此,其相應的極限環特性和穩定魯棒性能也都是相近的.那么可以自然地弓申出一個問題,即在怎樣的觀測器參數化帶寬關系下降階和全階ESO 之間的性能最為接近.首先考慮傳統的-3 dB 定義的物理帶寬,當兩者的物理帶寬相同時,降階和全階ESO 的參數化帶寬ωor和ωof之間滿足ωof=1.26ωor,顯然此時不滿足性能相似要求(表1 中的帶寬關系).這里我們嘗試用衡量線性系統相似性的ν 間隙度量[44]來計算兩個ESO 參數化帶寬之間的關系.兩個線性系統P1和P2之間的ν 間隙度量定義為

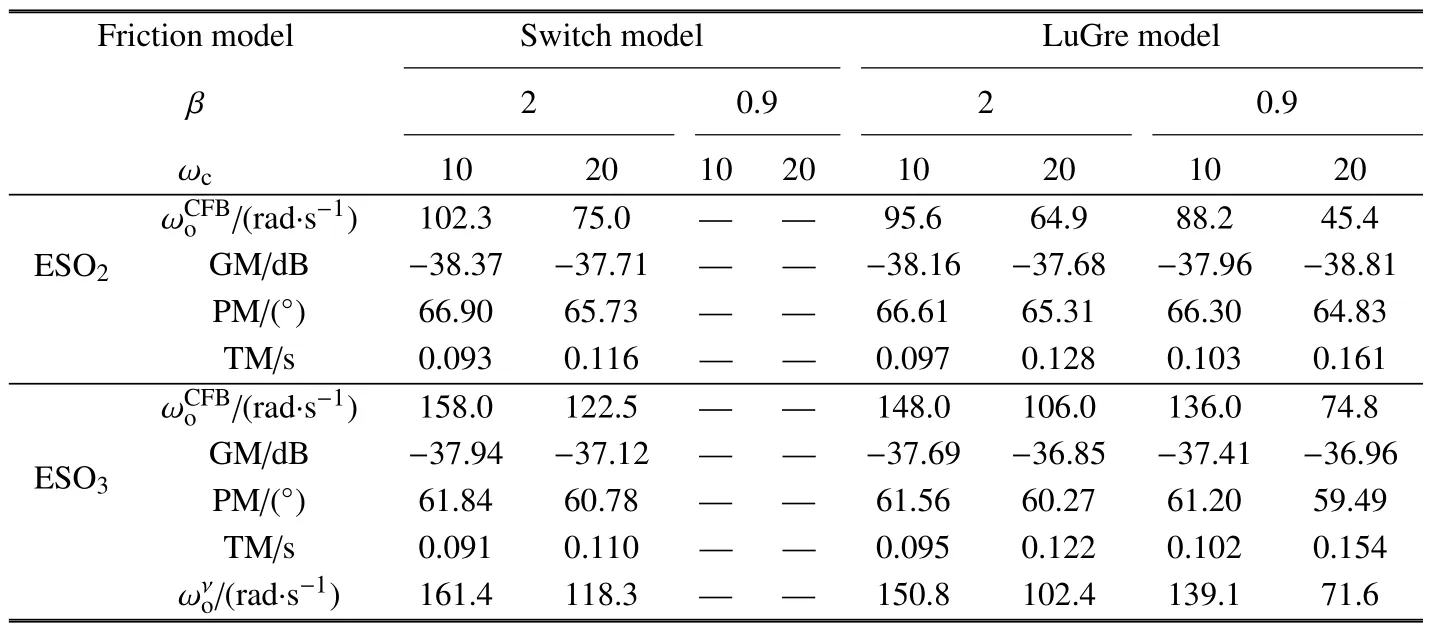
表1 全降階ESO 下的計算結果對比Table 1 Comparisons of calculation results for full-and reduced-order ESOs

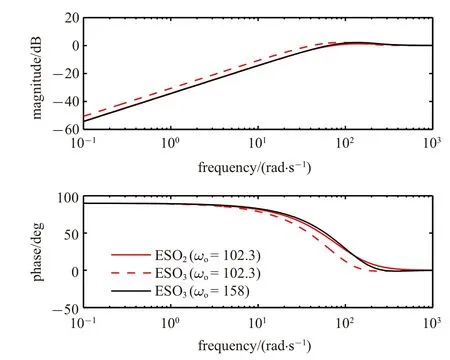
圖12 全降階ESO 的擾動估計誤差的頻率響應Fig.12 Frequency responses of disturbance estimation errors for full-and reduced-order ESOs

5 結論

本文得到以下四個主要結論.其中,結論(1) 和結論(2)總結了ADRC 階次的影響,結論(3)和結論(4)總結了摩擦力模型和參數以及控制參數的影響.

(1)當設計一階RESO 時,由于等效控制律即為PID 控制,已有的PID 控制下極限環振動結論直接適用.當設計二階RESO 時,等效閉環系統增加誤差濾波狀態.當設計全階ESO 時,等效閉環系統增加誤差濾波狀態及其導數.在這兩種情況下,雖然階次分別升高一階和兩階,對于給定的摩擦力模型,閉環系統極限環的存在性和穩定性、平衡點集的穩定性的結論和PID 控制下的結論仍然相同,反映了ADRC 階次對定性結論沒有影響.

(4)對于連續的LuGre 模型,當β=2 和β=0.9時,系統都會出現CFB,即極限環可以通過增大觀測器帶寬消除.當β=2 時,結果和切換模型β=2 時結果十分相近.然而當β=0.9 時,結果和切換模型β=0.9 時結果正好相反.

下一步將對低速斜坡指令跟蹤任務下的黏滑(stick slip) 振動展開研究.跟蹤低速斜坡指令時,系統變為非自治系統,文中方法不再適用,其周期解求解將會更加困難,這也是未來的研究重點.