一維準晶功能梯度層合圓柱殼熱電彈性精確解1)

李楊 秦慶華 張亮亮 高陽,2)

*(中國農業大學理學院,北京 100083)

?(澳大利亞國立大學工程與計算機科學學院,澳大利亞堪培拉2601)

引言

層狀結構因其優異的性能被廣泛應用于航空、航天、土木和機械等領域[1].常規的層狀結構是由均質材料層組合而成,以期獲得更好的機械和熱力學性能.但是,這種層狀結構界面處材料參數的突然變化會產生較大的層間應力,從而導致應力集中、裂紋和分層等問題.為了克服這些不利影響,科學家們提出功能梯度材料的概念,即利用連續變化的組分梯度來代替突變界面,進而消除界面處的物理性能突變,達到提高結構強度和優化結構性能的目的[2-3].鑒于功能梯度材料具有組成結構連續變化和可設計性的特點,越來越多的科研人員對功能梯度材料表現出極大的興趣.仲政等[2]對功能梯度材料與結構若干力學問題的最新研究進展進行了綜述,并對非均勻介質力學研究進行了展望.柯燎亮和汪越勝[3]結合功能梯度材料接觸力學的若干基本問題,綜述了相關理論的研究進展.鄭保敬等[4]提出一種模型降階方法用于分析非均質材料結構在復雜載荷作用下的動態響應.楊健鵬和王惠明[5]研究了功能梯度球形水凝膠在一定條件下的非均勻大變形溶脹行為.Yang 等[6]利用復變函數方法研究了含有功能梯度層加固橢圓孔的無限大板的應力集中問題,并獲得了其通解.基于廣義England 方法,Yang 等[7]研究了功能梯度圓板在中心承受集中力作用下的軸對稱彎曲問題.Pan 和Han[8]提出類Stroh 理論用于研究功能梯度磁電彈層合板的彎曲問題,獲得了材料常數沿厚度方向呈現指數函數分布的精確解.

準晶由以色列科學家Shechtman 教授首次在急冷的Al-Mn 合金電子衍射圖形中發現[9].準晶是一種不同于晶體和非晶體的新型固體材料,具有長程有序的原子排列,但不具備平移對稱性[10].基于Landau 的元激發唯象理論,準晶中存在兩個低能元激發:聲子和相位子[11-12].相位子場的弓入,使準晶表現出不同于晶體和非晶體的多種性能,如:高強度、高硬度、耐磨性、耐腐蝕、低摩擦系數和低導熱率等[13-14].由于準晶表現出來的優異性能,其主要用作表面涂層、薄膜以及復合材料增強相[15].隨著準晶應用的推廣,準晶材料的性能研究受到許多學者的關注.Maugin[16]將提出的準晶彈性方程擴展到準晶熱彈性問題中.Li 等[17]利用廣義勢能理論,研究了二維六方準晶中的三維熱彈性平面裂紋問題,并獲得了解析解.Guo 等[18]基于Stroh 理論,研究了二維十次熱彈性準晶的缺陷問題.Li 等[19-20]分別給出了考慮熱效應的一維六方壓電準晶中平面裂紋問題的理論解和數值解.

層合圓柱殼具有重量輕、強度高等特點,是工程中常用的結構元件之一.目前,關于準晶層狀結構的動態和靜態問題研究多數是基于矩形層合板開展的[21-23].此外,同時考慮熱電彈耦合效應和材料不均勻性的準晶層合圓柱殼的研究開展的很少.因此,本文采用類Stroh 理論和傳遞矩陣方法,獲得了一維準晶功能梯度層合圓柱殼的熱電彈性精確解,討論了功能梯度指數因子對層合圓柱殼物理量的影響,以期為準晶功能梯度層合圓柱殼的多場耦合效應及非均勻性分析提供可靠的參考依據.

1 基本方程

圖1 是柱坐標系(r,θ,z)中一維準晶功能梯度層合圓柱殼的示意圖,準周期方向和極化方向均沿著r軸,其外表面半徑為rb,內表面半徑為ra,沿z向長度遠遠大于層合圓柱殼半徑,層合圓柱殼的角度跨度為θ0,第j層的內外半徑分別為rj和rj+1.

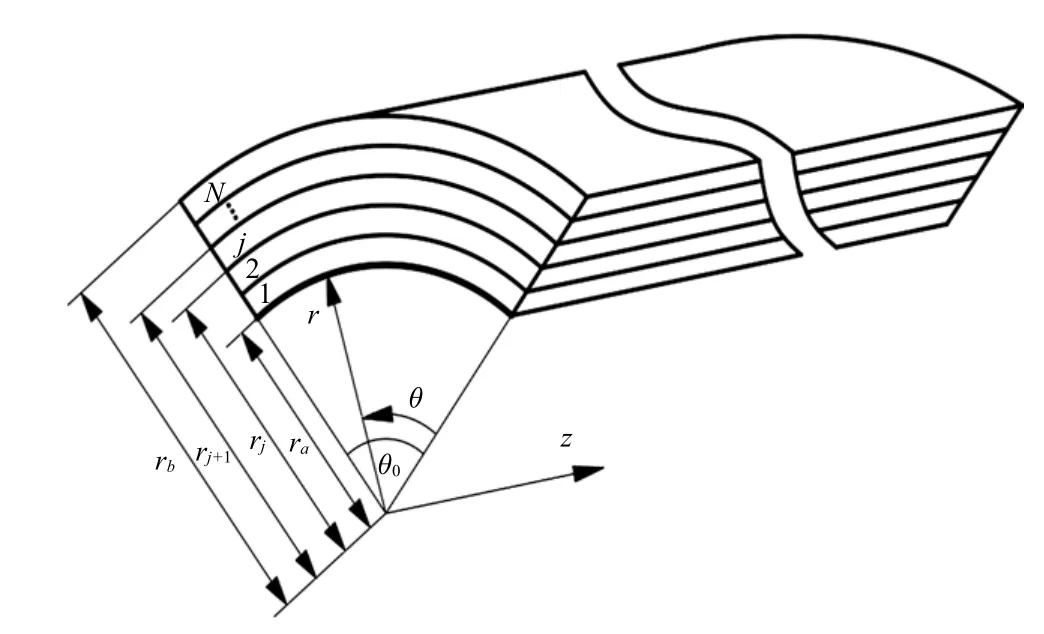
圖1 一維準晶功能梯度層合圓柱殼的示意圖Fig.1 Schematic of functionally graded layered 1D quasicrystal cylindrical shells

對于考慮熱-電-彈耦合的一維正交準晶材料,本構方程為[24]

式中,σkl為聲子場應力; εkl為聲子場應變;Hil為相位子場應力;wil為相位子場應變;Dk為電位移;Ek為電場強度;T為溫度變化;Ckl,Rkl,Kkl分別為聲子場彈性常數,聲子場-相位子場耦合彈性常數和相位子場彈性常數;ekl,dkl,ξll分別為聲子場壓電系數,相位子場壓電系數和介電系數;p3和βk分別為熱電系數和導熱系數.

忽略體力、自由電荷以及內部熱源,靜態平衡方程可寫為

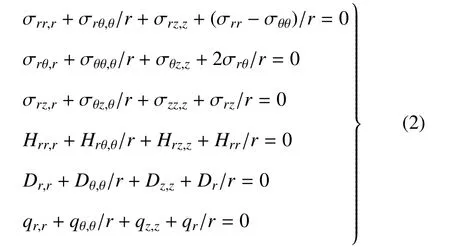
式中,qr,qθ,qz為熱流.熱流與溫度的關系,可以表示為[25]

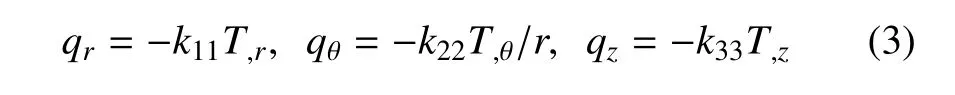
式中,kll為熱傳導系數.幾何方程為

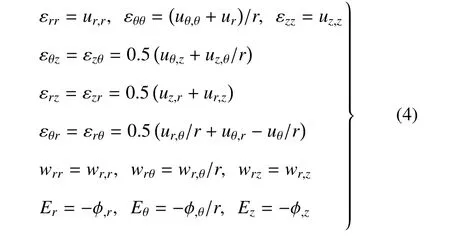
式中,ur,uθ,uz為聲子場位移;wr為相位子場位移;φ 為電勢.考慮層合圓柱殼兩側邊簡支的邊界條件[24],即

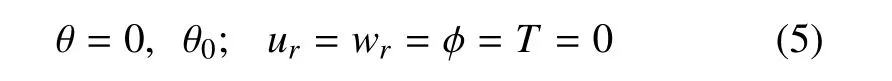
對于一維準晶功能梯度材料,假設其材料參數沿著徑向呈現冪函數分布,即

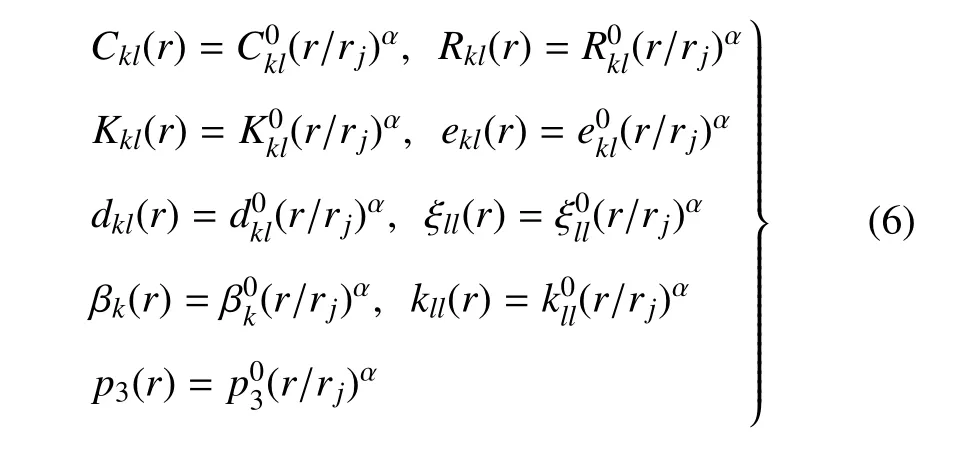
式中,α 為功能梯度指數因子,表示材料參數在半徑r方向的梯度分布程度,后文中α 均表示功能梯度指數因子;上標帶“0”的物理量表示均質材料對應的材料參數.

2 單層圓柱殼的熱電彈性精確解

2.1 溫度場的精確解

滿足兩側邊簡支邊界條件的溫度函數可假設為

式中,ρ=r/rj,p=mπ/θ0,ˉT(r)為與圓柱殼角度θ 無關的溫度,文中其他頂部帶橫線的物理量均表示獨立于圓柱殼角度的物理量.

將式(7)代入式(3),然后代入式(2),得

式中,特征值η 可求解為

將式(8)所示特征關系改寫成

利用特征值和特征向量,可得到一維準晶功能梯度單層圓柱殼溫度場的精確解

式中,χ1和χ2為待定未知量.

2.2 電彈耦合場的精確解

對于簡支層合圓柱殼,廣義位移矢量可表示為

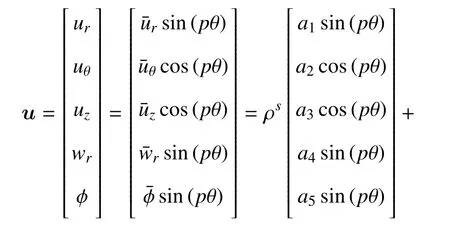
將式(12)代入式(4),然后代入式(1),得到徑向的廣義應力矢量

弓入4 個矢量

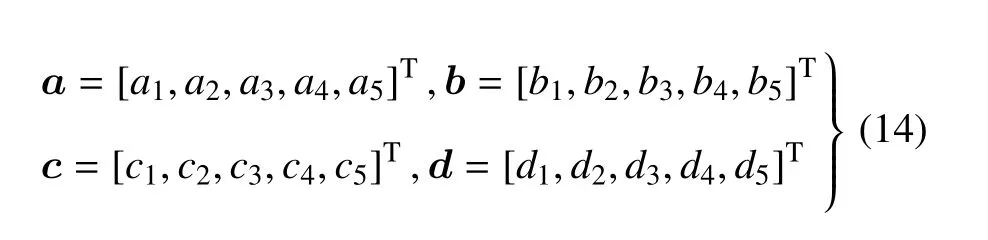
式(14)所示矢量存在如下關系

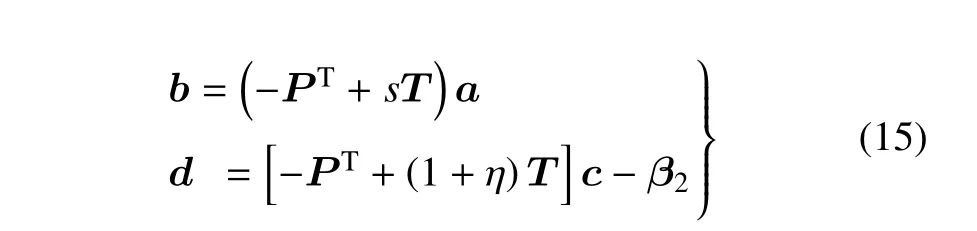
利用基本方程和式(12),推導出滿足一維熱-電-彈性準晶功能梯度層合圓柱殼的類Stroh 公式[26]

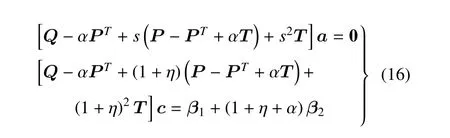
式(15)和式(16)中矩陣分別為

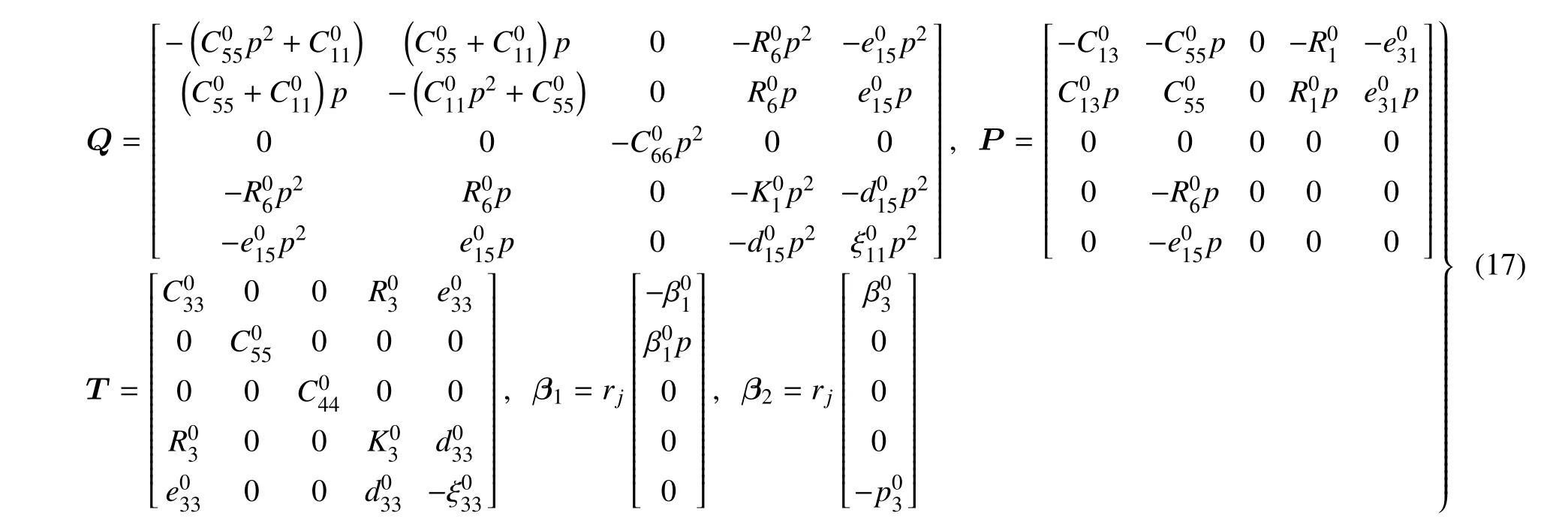
為了便于求解,將式(16) 轉換為對應的標準特征關系

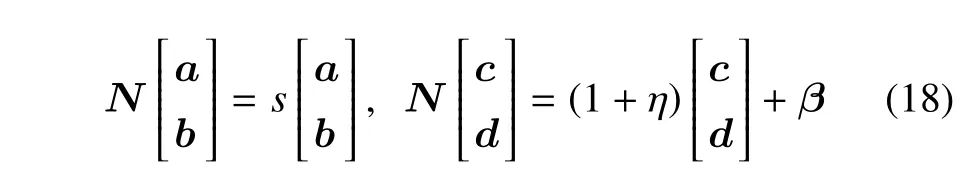
式中,矩陣N和β分別為

求解式(18),可得到電-彈耦合場對應的特征值s和特征向量[a b]T,[c d]T.因此,一維準晶功能梯度單層圓柱殼電-彈耦合場的精確解為

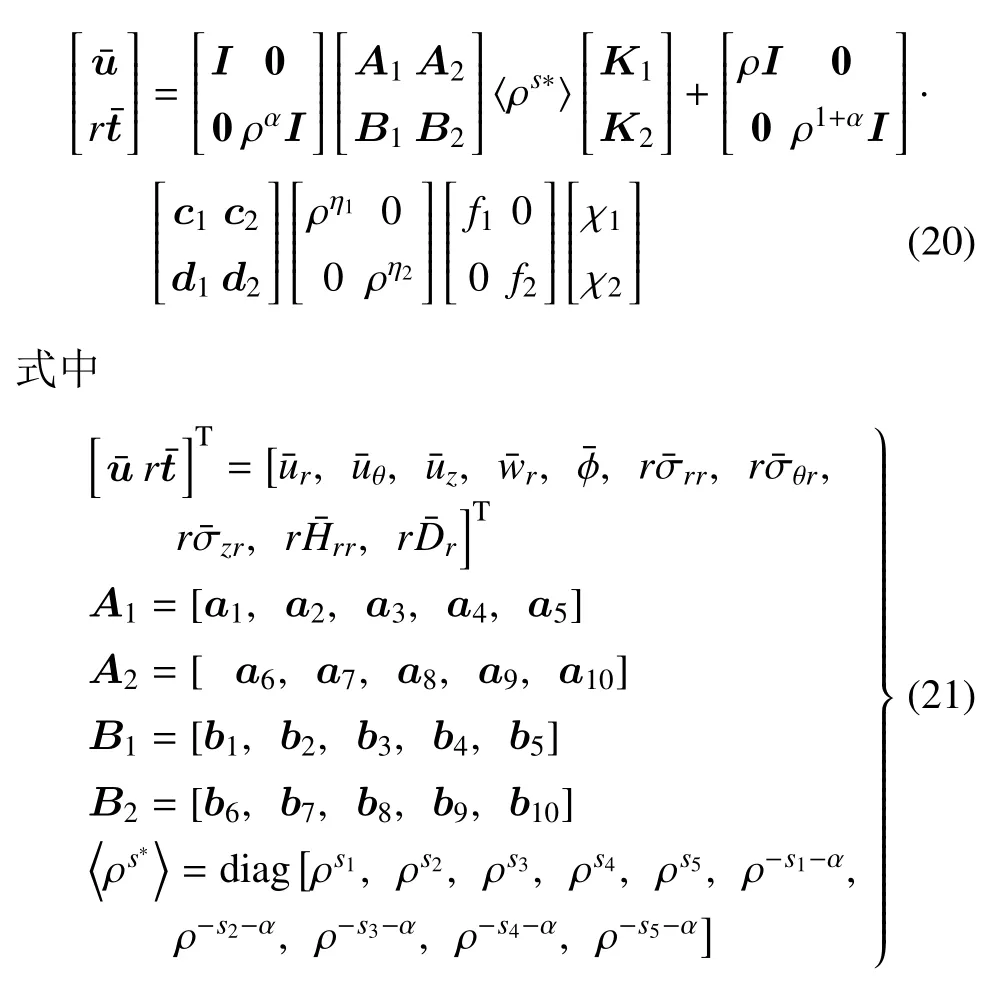
3 層合圓柱殼的熱電彈性精確解

本節弓入傳遞矩陣方法[26],用于處理層狀結構問題.假設層間界面為完美連接,首先處理溫度場的傳遞問題,然后求解電-彈耦合場多層結構問題,最后將溫度場、電場和彈性場的結果合并,得到一維準晶功能梯度層合圓柱殼的熱-電-彈性精確解.

考慮溫度場,對于層合圓柱殼第j層,利用式(11),有

利用式(22),圓柱殼j層任意半徑處的物理量為

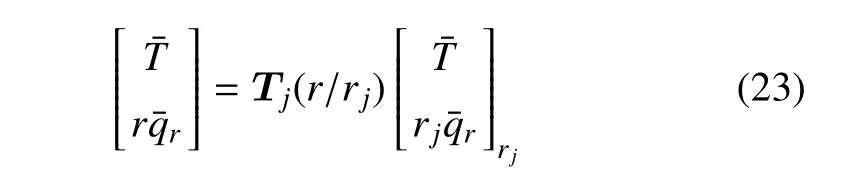
式中,溫度場的傳遞矩陣Tj為

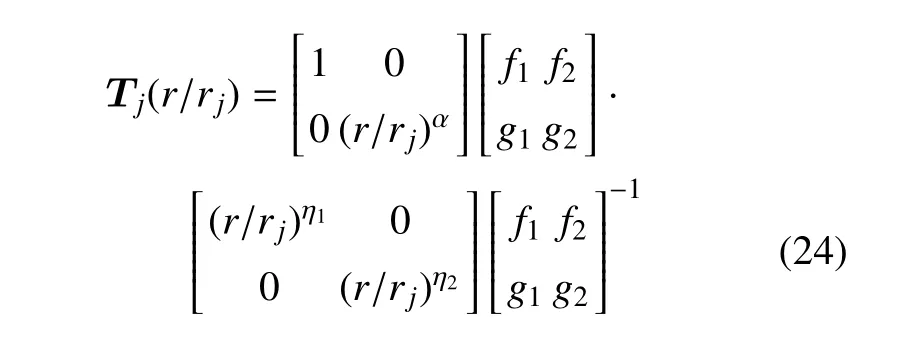
考慮電-彈耦合場,對于圓柱殼j層,借助式(20),可以得到

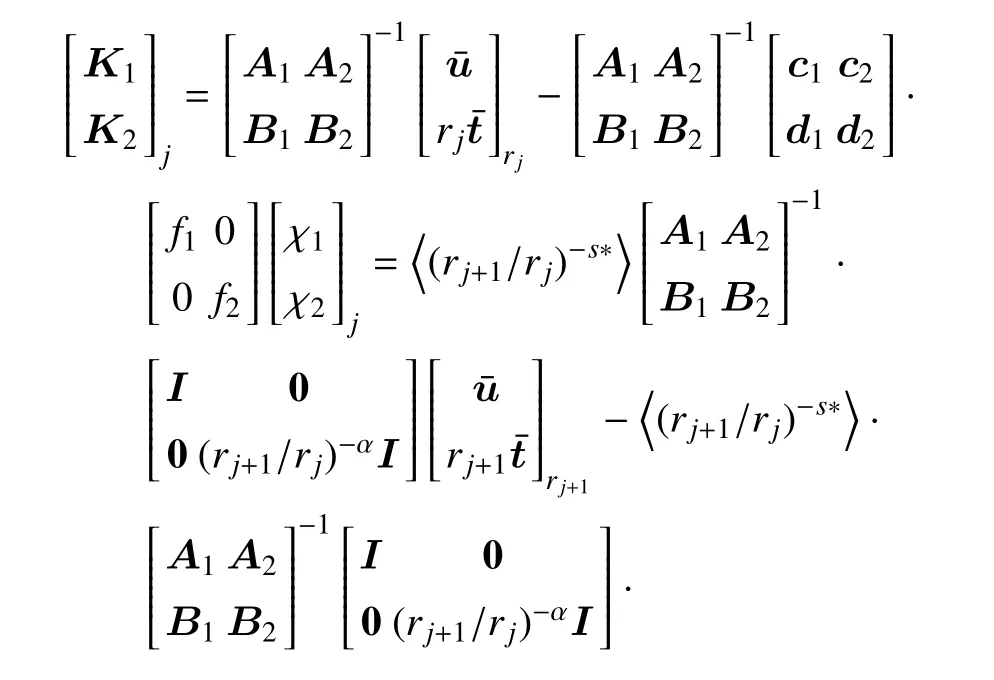
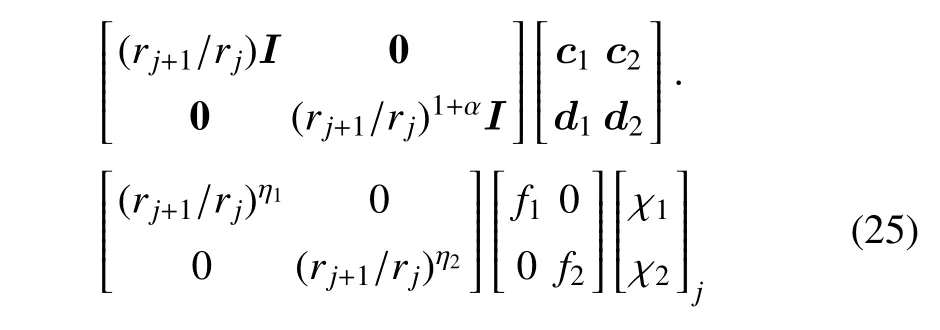
利用式(25),層合圓柱殼j層任意半徑處的物理量可以表示為

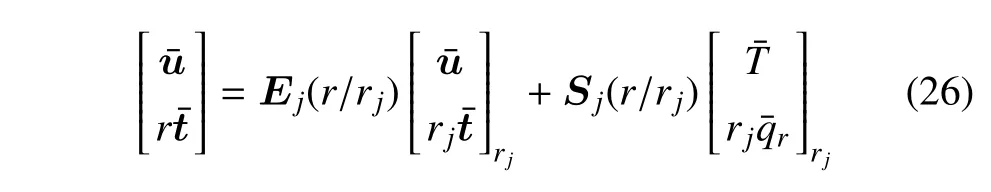
式中,矩陣Ej和Sj分別為

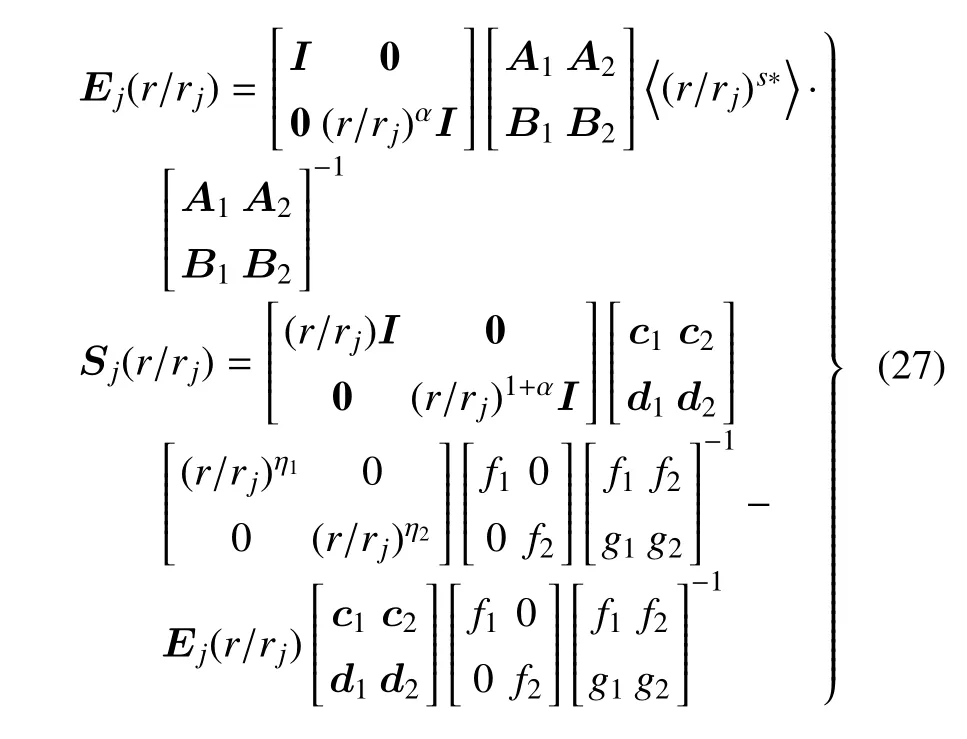
將式(23) 和式(26) 中精確解合并,同時重復利用傳遞矩陣,得到一維準晶功能梯度層合圓柱殼的熱電彈性精確解

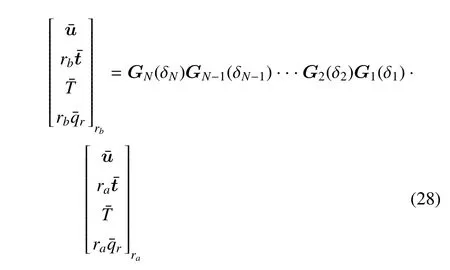
式中,δj=rj+1/rj,傳遞矩陣Gj(δj)為

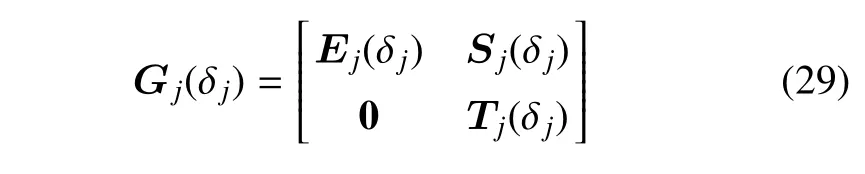
4 數值算例

本節主要討論功能梯度指數因子對溫度場、電場、聲子場和相位子場的影響.考慮3 層功能梯度圓柱殼,第一層和第三層為功能梯度準晶材料Al-Ni-Co,第二層為均質壓電材料BaTiO3,且每層厚度相等,材料常數見表1[27-29].計算中為避免產生奇異矩陣,晶體的相位子場彈性常數按照10-8倍的準晶相位子場彈性常數選取[30],同時晶體中聲子場-相位子場耦合彈性常數為0.

表1 材料常數Table 1 Material Constants

層合圓柱殼的幾何參數為:內表面半徑ra=4 mm,外表面半徑rb=10 mm,角度跨度θ0=1 rad.假設在功能梯度層合圓柱殼的內外表面同時施加溫度載荷,外表面載荷為T(rb)=1K,內表面載荷為T(ra)=0.5K.令m=1,指數因子分別為α=-5,0,5.當α=0 時,功能梯度材料退化為均質材料.數值算例中給出的物理量均獨立于圓柱殼角度θ.

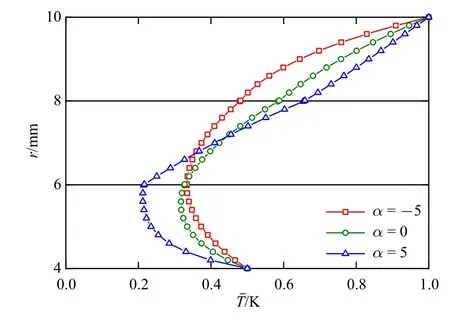
圖2 指數因子對溫度的影響Fig.2 Influence of exponential factor on temperature

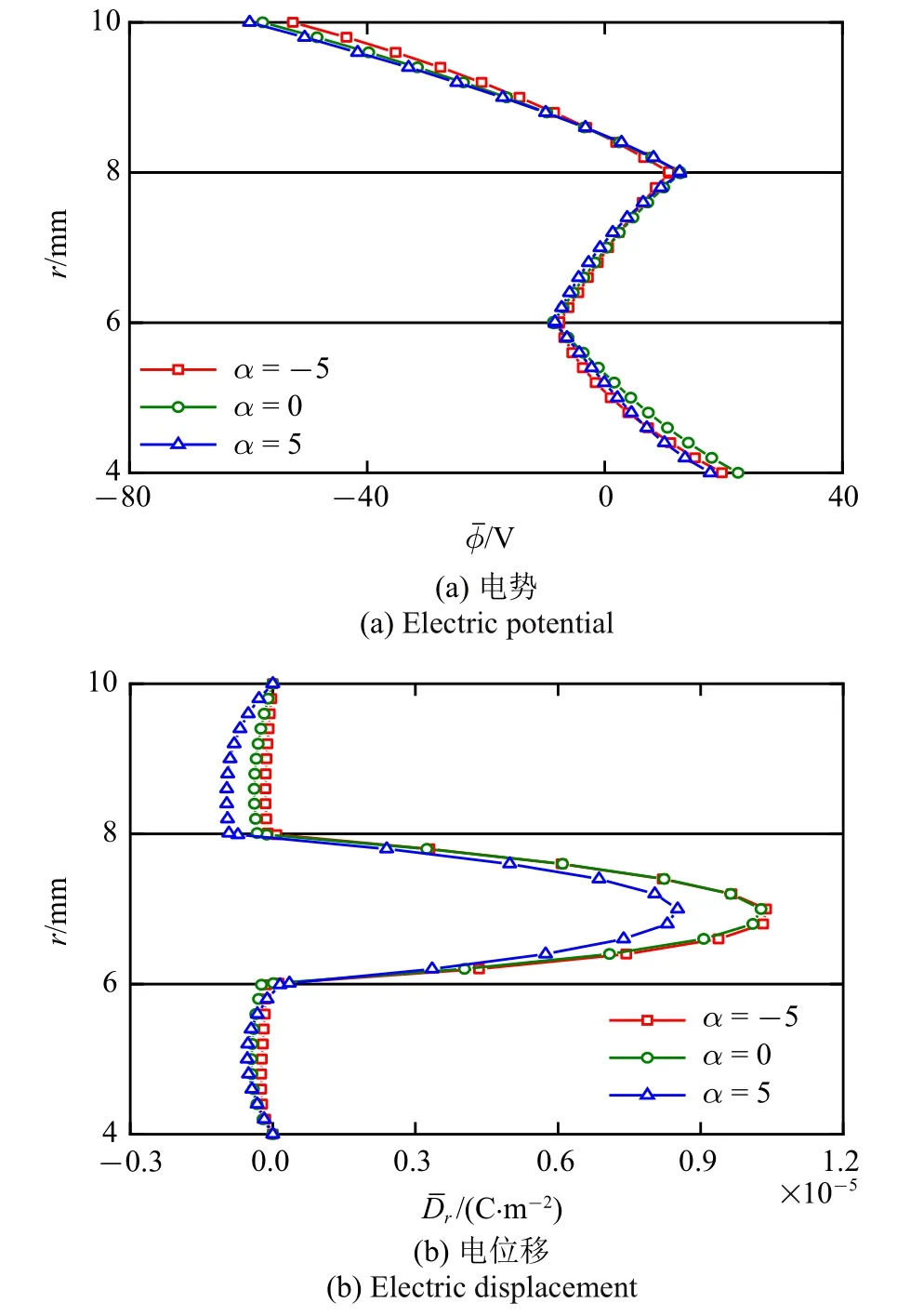
圖3 指數因子對電場的影響Fig.3 Influence of exponential factor on electric field

圖4 為不同指數因子α 對應的聲子場和相位子場應力沿半徑方向的變化曲線.圖4(a) 為在圓柱殼界面處連續的聲子場應力.和α=-5 對應的相比,α=5 對應的最大值更大.此外,α=5 對應的在靠近內表面處數值最小,在靠近外表面處數值最大.從圖4(b)可以看到,相位子場應力在中間層為0,因為晶體中不存在相位子場.準晶層中的隨著α 的增大而增大.

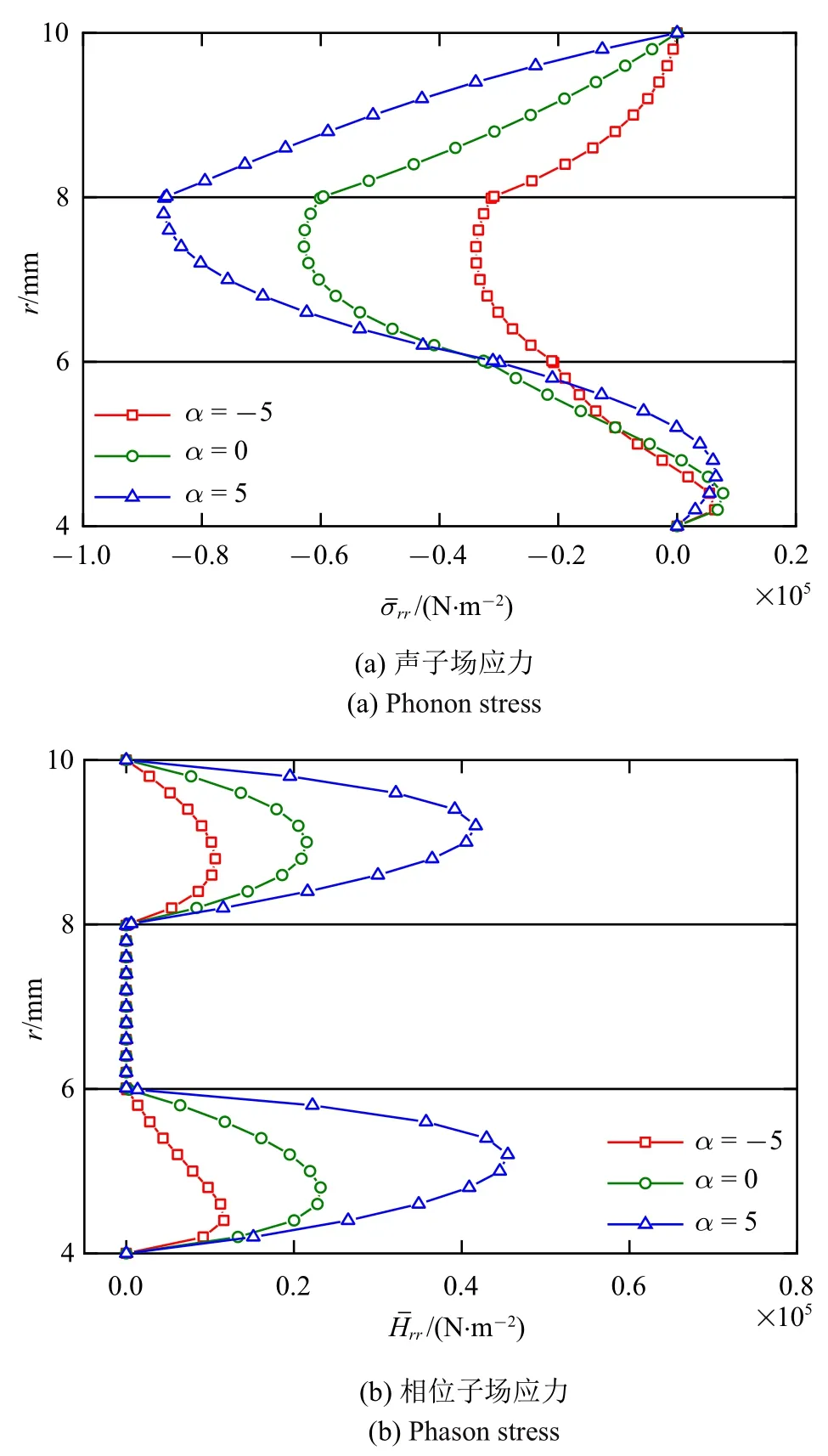
圖4 指數因子對聲子場和相位子場應力的影響Fig.4 Influence of exponential factor on phonon and phason stresses

圖5 給出指數因子α 對聲子場和相位子場位移的影響.圖5(a)顯示聲子場位移在界面處是連續的.文中功能梯度材料參數遵循冪函數變化規律,當指數因子α ＞0 時,功能梯度材料性質呈現漸變硬化趨勢,α ＜0 則呈現漸變軟化特性.所以層合圓柱殼內表面隨著α 增大而變小.同時,的大小還與層合圓柱殼半徑有關.因此,不同的指數因子對應的在最外層出現交點.此外,和α=-5 對應的相比,α=5 對應的在界面處曲線更光滑.在圖5(b)中,和α 對的影響相比,α 對內外表面處的相位子場位移的影響較小.

圖5 指數因子對聲子場和相位子場位移的影響Fig.5 Influence of exponential factor on phonon and phason displacements

5 結論

本文利用類Stroh 理論和傳遞矩陣方法,研究了一維準晶功能梯度層合圓柱殼的熱電彈性耦合問題,基于材料參數沿徑向呈現冪函數分布特點,得到了簡支邊界條件下的一維準晶功能梯度層合圓柱殼的熱電彈性精確解.數值算例中討論了功能梯度指數因子對溫度場、電場、聲子場和相位子場的影響.所得結論如下:

(1)指數因子的變化影響層合圓柱殼的材料性質分布情況,進而對溫度、電勢、電位移、聲子場和相位子場應力和位移產生較大的影響.

(2)隨著指數因子的增大,徑向聲子場應力增大,且最大值出現在層合圓柱殼外層.外層中較大的應力易于被外層凸面分散,從而提升層合圓柱殼的承載能力.

(3)隨著指數因子的增大,層合圓柱殼外表面周向聲子場位移略有增大,內表面周向聲子場位移減小.此外,周向位移在界面處更為光滑,可有效減緩層合圓柱殼在界面處出現開裂和分層等現象.