n 類相依保險業務下的最優再保險和投資

楊 鵬， 陳 鑫

(1- 西京學院理學院，西安 710123; 2- 西安交通大學數學與統計學院，西安 710049;3- 人民日報海外網，北京 100733)

1 引言

保險公司通過再保險可以減少理賠風險，通過在金融市場上投資可以增加財富，因此再保險和投資對保險公司來說非常重要.近年來，國內外很多學者研究了最優再保險和投資問題.他們研究的優化準則主要包含：最大化終值財富的期望效用，最小化破產概率和最大化終值財富的均值同時最小化終值財富的方差(即，均值-方差準則).因為均值-方差準則是雙目標優化問題，通過均值可以衡量保險公司的收益，通過方差可以直接衡量保險公司的風險，因此，均值-方差準則越來越受到學者們推崇.

均值-方差準則首次由美國經濟學家和數學家Markowitz 在1952 年提出[1].Markowitz用均值-方差準則研究了投資組合問題，由于他對該問題的卓越研究，獲得了1990 年諾貝爾經濟學獎.Markowitz 考慮的模型是離散時間的，Zhou 和Li[2]把均值-方差投資組合問題推廣到了連續時間.自從Zhou 和Li[2]之后，很多學者把連續時間均值-方差準則應用到再保險和投資問題中.B¨auerle[3]較早的考慮了均值-方差準則下的最優再保險問題.Bai 和Zhang[4]在Cram′er-Lundberg 和擴散逼近兩種保險模型下，研究了均值-方差準則下的最優再保險和投資問題.楊鵬等[5]在Poisson-Geometric 保險模型下，研究了均值-方差準則下的最優再保險和投資問題.Liang 等[6]在保險市場和金融市場相依下，研究了均值-方差準則下的最優再保險和投資問題.Bi 等[7]在兩個相依類的保險業務中，研究了均值-方差準則下的最優再保險和投資問題.楊鵬[8]在Ornstein-Uhlenbeck 模型中，研究了均值-方差準則下的最優再保險和投資問題.Sun 和Guo[9]在風險資產價格滿足Cox-Ingersoll-Ross 模型時，研究了均值-方差準則下的最優再保險和投資問題.Bi 等[10]在Markov 鏈調制的保險市場和金融市場上，研究了均值-方差準則下的最優再保險和投資問題.

上述文獻在均值-方差準則下得到的最優再保險和投資策略只在初始時刻是最優的，隨著時間的進行策略則不是最優的了，文獻中把這種策略稱為預先承諾(precommitment)的策略.Strotz 在1955 年[11]首次使用博弈論的思想研究了時間不一致性，他指出時間不一致的問題可以通過預先承諾的策略和時間一致的策略兩種方法求解.在保險實務中，保險公司每天的偏好有可能是不同的，但是在很多情形下，他們追求的最優策略基本保持一致.因此，研究時間一致的策略在保險實務中具有很重要的現實意義.Bj¨ork 和Murgoci[12]基于博弈論的思想，對于一個通常的Markov 過程提出了求解時間一致策略的方法.Bj¨ork 和Murgoci[12]之后，近十年來有很多學者在時間不一致的均值-方差問題中，研究了時間一致的再保險和投資策略.Li 等[13]在Heston 模型下，研究了時間一致的再保險和投資策略.Lin 和Qian[14]在CEV 模型下，研究了時間一致的再保險和投資策略.Yang[15]在保險市場與金融市場相依情形下，研究了時間一致的再保險和投資策略.Wang 等[16]在保險模型和金融市場模型的參數都是隨機的情形下，研究了時間一致的再保險和投資策略.Zhu 等[17]對于兩個保險公司，在考慮他們的相對業績情形下，研究了時間一致的再保險和投資策略.Yang 等[18]在聯合比例和超額損失再保險下，研究了時間一致的再保險和投資策略.

本文剩下的結構如下：第2 節給出了保險模型和金融市場模型，以及后文中用到的一些假設.第3 節，給出了時間不一致的均值-方差問題.第4 節，首先建立了推廣的HJB 方程，進而通過求解推廣的HJB 方程，得到了最優時間一致的再保險和投資策略以及值函數的顯式解.第5 節，通過數值實驗解釋了模型參數對最優時間一致的再保險和投資策略的影響，并分析了這些影響背后的經濟意義.最后一節，總結了全文.

2 模型和假設

本節我們給出保險模型和金融市場模型以及一些假設.為了使數學上更為嚴格，設(Ω，F，P)是完備的概率空間，它滿足通常條件，也就是F = {Ft，t ∈[0，T]}是右連續的且關于P 是完備的，T ＞0 是再保險和投資的終止時間，Ft是到時刻t 為止，保險公司所獲取的所有信息.本文不考慮交易費用和稅收，所有資產都是無窮可分的.

2.1 保險模型

我們假設一個保險公司從事n ≥2 類相互依賴的保險業務，后文中稱為保險業務1，2，··· ，n.Zij(i = 1，2，··· ， j = 1，2，··· ，n)是相互獨立、同分布、取正值的隨機變量，它代表保險業務j 的第i 次理賠額.記Zij的通常隨機變量為Zj，它的一階和二階矩分別記作E(Zj) = μ1j和E[(Zj)2] = μ2j.基于這些設定，到時刻t 為止，保險業務j 的累積理賠額可表示為

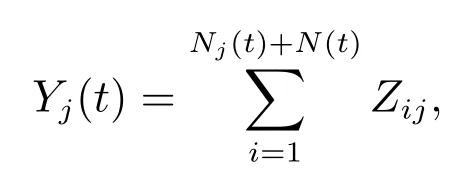
注2n 類保險業務的相依性，通過共同的泊松過程N(t)來刻畫.模型(1)是帶跳的，Sun 等[19]用幾何布朗運動逼近模型(1)，也就是說Sun 等[19]用連續的模型來近似帶跳的模型.他們這樣處理有一些局限性，正如我們在引言中分析的，考慮帶跳的累積理賠過程更符合實際.據我們所知，本文首次研究了n 類相依保險業務帶跳的情形.

保險公司為了規避理賠風險，它尋求一家再保險公司進行再保險.假設保險公司采取比例再保險，它的基本思想是：對于保險業務j 的第i 次理賠額Zij，保險公司支付aj(t)Zij，剩余的理賠額(1-aj(t))Zij由再保險公司賠付，這里aj(t) ∈[0，1]是保險公司的自留比例，稱為自留額.由于再保險公司為保險公司賠付了理賠額(1-aj(t))Zij，作為補償，保險公司向再保險公司支付一定的費用，記為(1-aj(t))cj.cj＞0 是完全進行再保險時，保險公司向再保險公司支付的費用.這里假設cj＞ˉcj，即對于每類業務j，再保險要比保險貴，這在保險實務中是有意義的，否則保險公司存在套利行為.記a(t) = (a1(t)，a2(t)，··· ，an(t))，則考慮再保險后，保險公司在時刻t 的盈余過程Xa(t)滿足下面的微分方程

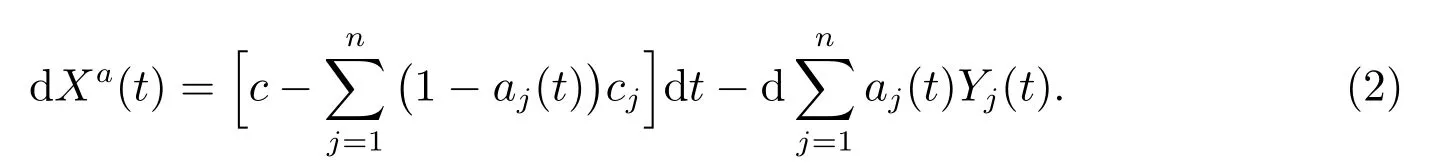
2.2 金融市場

保險公司除了再保險，還可以在金融市場上進行投資.金融市場由一個無風險資產和n 個相依的風險資產組成.在時刻t，無風險資產的價格為B(t)，B(t)滿足微分方程dB(t) = rB(t)dt.這里r ＞0 為無風險資產的利率.在時刻t，風險資產i， i =1，2，··· ，n 的價格為Si(t)，Si(t)滿足如下隨機微分方程

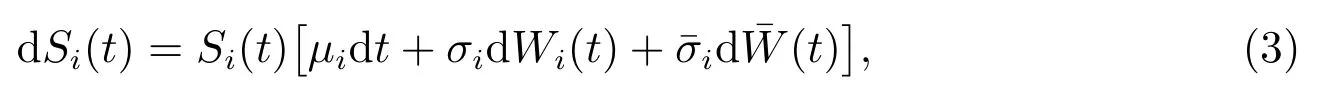
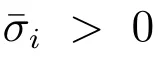
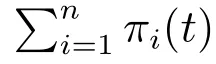
為了獲得最優的再保險和投資策略，下面定義可行的再保險和投資策略集.

定義1一個策略u(·)=(a1(·)，a2(·)，··· ，an(·)，π1(·)，π2(·)，··· ，πn(·))稱為可行的，如果u(·)關于流Ft是可料的，且對于每個t ≥0 過程u(·)滿足條件：

(iii) 隨機微分方程(4)對于u(t)有唯一的強解Xu(t)；

(iv) 對于任意的? ≥1， E[sups∈[t，T]|Xu(s)|?]＜+∞.

我們把所有可行的策略記為U.

3 時間不一致的均值-方差問題

傳統的均值-方差問題如下

這里

γ ＞0 表示保險公司的風險厭惡參數.該問題只給出了最初時刻的優化目標，所以不是動態的.目標函數在將來有可能變化，因此研究當目標函數隨著時間改變時的最優化問題更有意義.本文研究如下動態的目標函數

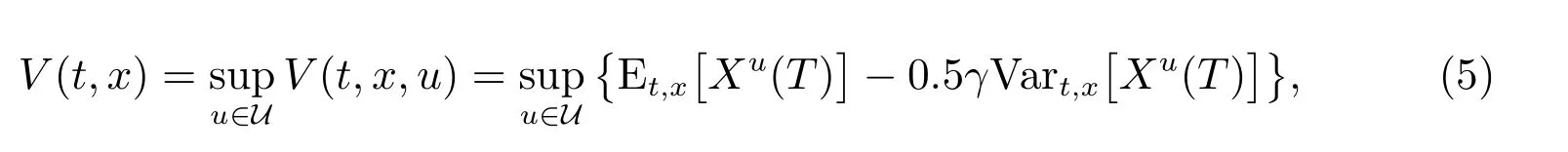
這里

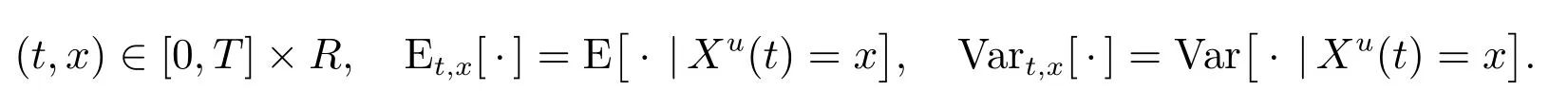
問題(5)中含有方差項Vart，x[Xu(T)]，這導致期望的迭代性不滿足，因此貝爾曼最優性原理不成立，所以該問題是時間不一致的.Strotz[11]指出，時間不一致的問題有兩種求解方法：一是通過求解預先承諾的策略求解時間不一致的問題，該策略是時間不一致的，例如，Zhou 和Li[2]使用了該方法；另一種方法是通過求解時間一致的策略求解時間不一致的問題，例如，Bj¨ork 和Murgoci[12]使用了該方法.人們的偏好可能會隨著時間的改變而改變，然而大多數情況下人們希望同一時刻的最優策略，在不同的時間所做的決策是一致的.因此，本文通過求解時間一致的策略求解時間不一致的問題(5).時間一致策略更精確的表述是：對于某固定的時刻s，假設t ＞s，若在時刻s 獲得最優策略u(t)使得問題(5)成立；那么到達時刻t 時，該策略u(t)仍是問題(5)的最優策略.

本文與Bj¨ork 和Murgoci[12]相似的，從博弈論的視角尋求時間一致的再保險和投資策略.具體來說，我們把該問題視為一個非合作的博弈，在每個時刻有一個博弈者.未來時刻t 的博弈者，可以被視為當前時刻保險公司在未來時刻t 的化身.與Bj¨ork 和Murgoci[12]相似的，我們給出如下均衡策略和均衡值函數的定義.

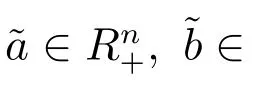
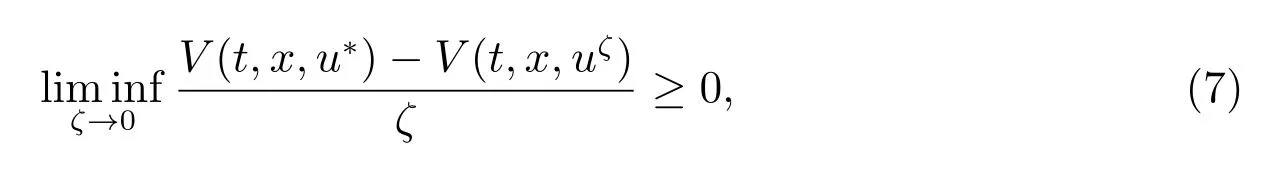
則u*(t)稱為均衡策略，相應的均衡值函數為V(t，x)=V(t，x，u*).

為了下文中書寫方便，我們定義一個記號D1，2([0，T]×R).它是由滿足下列條件的全體φ(t，x)組成：

(i) φ(t，x)和它的導數φt(t，x)， φx(t，x)，φxx(t，x)在[0，T]×R 上連續；

(ii) φ(t，x)和φx(t，x)滿足多項式增長條件，即存在兩個正常數κ 和p，使得|φ(t，x)|≤κ(1+|x|p)和|φx(t，x)|≤κ(1+|x|p).

為了求解問題(5)，我們利用隨機控制和隨機動態規劃技術建立如下的驗證定理.類似的定理在文獻中廣為使用，這里證明方法類似于Li 等[13]中的定理1 和Yang[15]中的定理4.1，我們這里不再給出證明.

定理1(驗證定理) 假設V(t，x)∈D1，2([0，T]×R)和h(t，x)∈D1，2([0，T]×R)是兩個實函數，它們滿足如下推廣的HJB 方程.

(i) 對于任意的(t，x)∈[0，T]×R，有

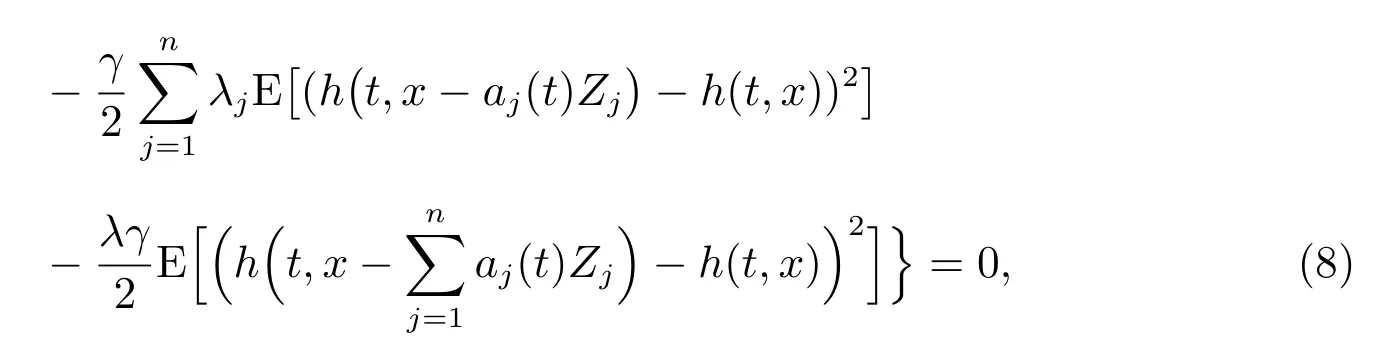
這里Vt和Vx分別表示V(t，x)關于t 和x 的一階偏導數，Vxx表示V(t，x)關于x 的二偏階導數.

(ii) 對于任意的(t，x)∈[0，T]×R，有

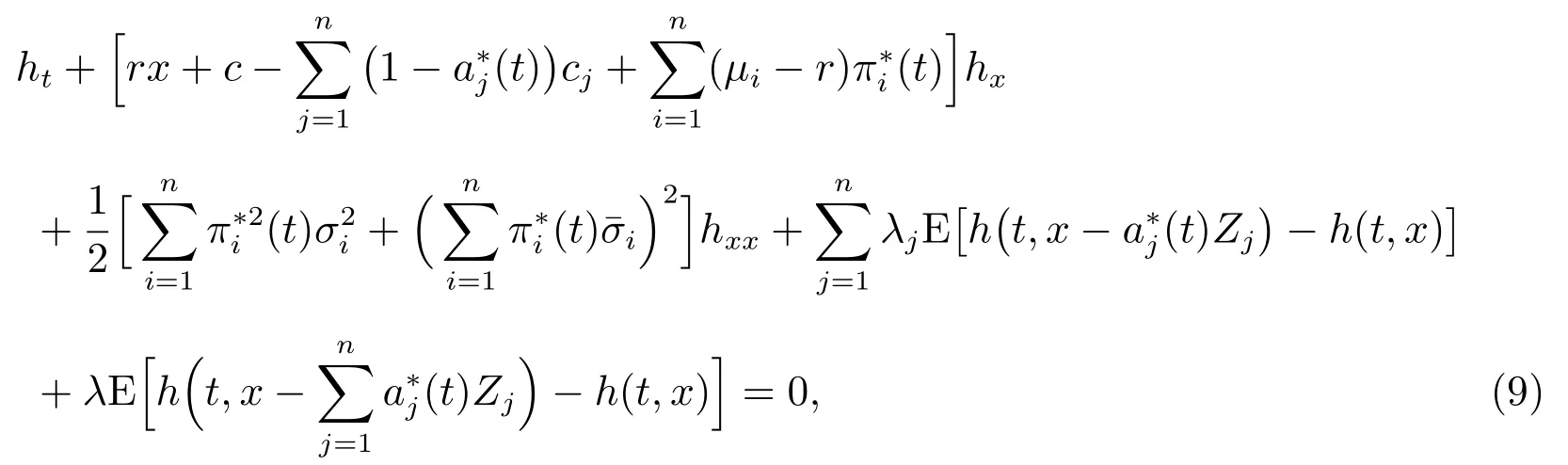
這里ht和hx分別表示h(t，x)關于t 和x 的一階偏導數，hxx表示h(t，x)關于x 的二階偏導數，u*(t)是(8)左端sup{···}內函數的最大值點.

(iii) 對于x ∈R，有

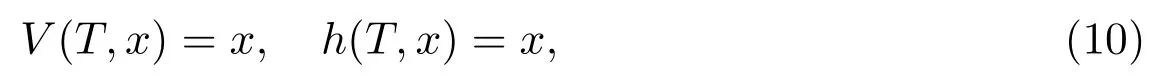
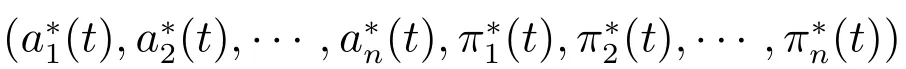
4 時間一致的再保險投資策略

本節的目的是，通過上一節的驗證定理，求得問題(5)的最優時間一致的再保險和投資策略.為了得到最優時間一致的再保險和投資策略，我們首先給出以下三個引理.

引理1值函數V(t，x)和終值財富的均值h(t，x)在均值-方差框架下，是關于x 的一次函數，它們有下面的形式

該引理的證明類似于Yang 等[18]中的引理4.1，這里不再給出證明.

引理2令

則下面的方程組

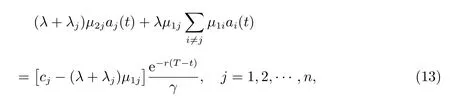
這里Δj定義為

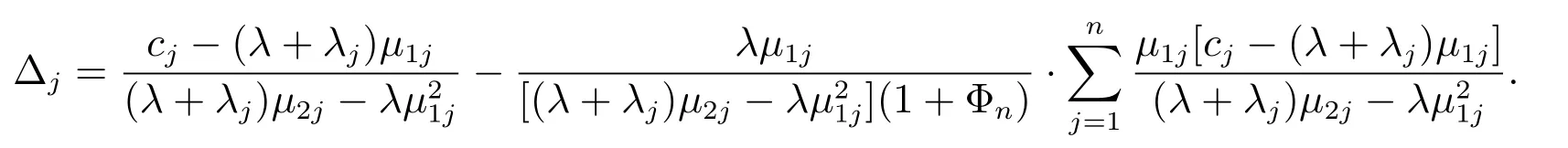
證明 方程組(13)可以等價的表示為

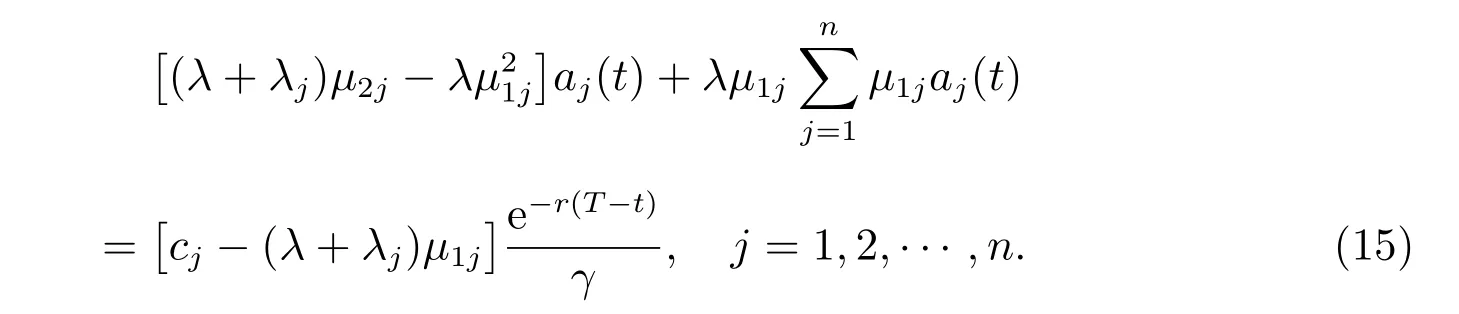
因為

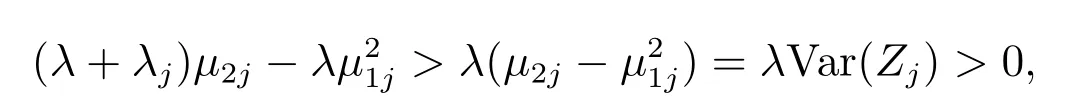
所以，方程組(15)等價于

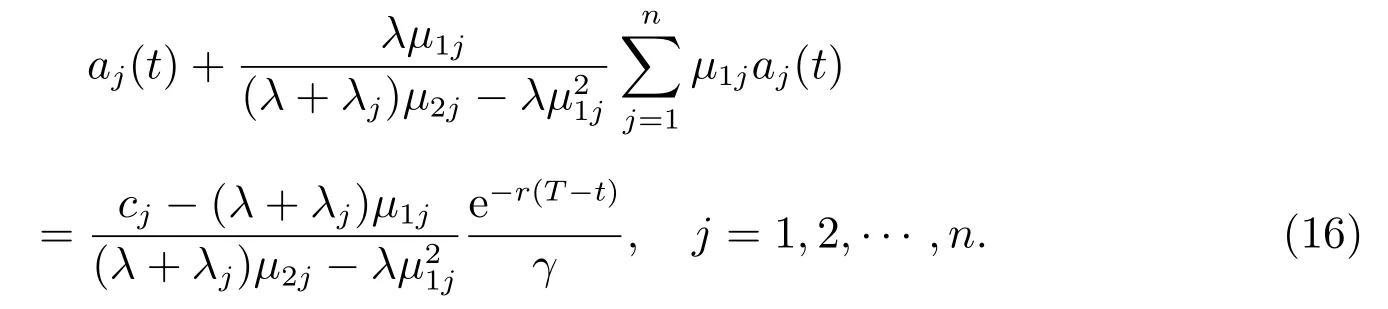
方程組(16)兩端同時乘以μ1j，并對j 從1 到n 求和得到

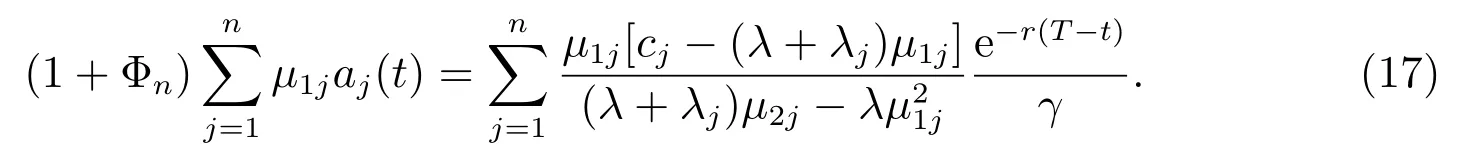
因為Φn＞0，所以由(17)式得到

把(18)式代入(16)式，我們得到方程組(13)的唯一解，唯一解由(14)式給出.

類似于引理2，我們可以得到下面的引理3.

引理3下面的方程組

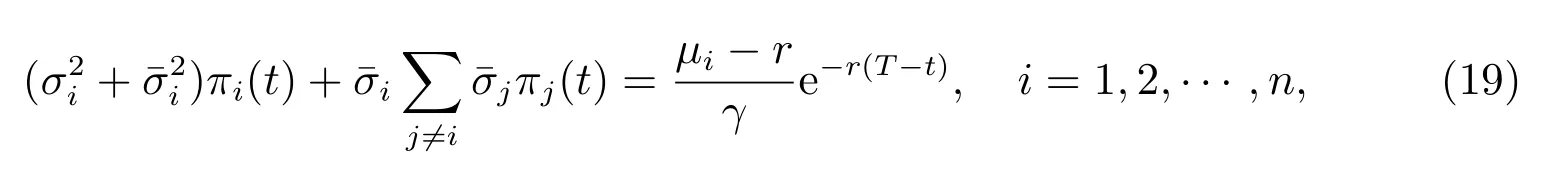
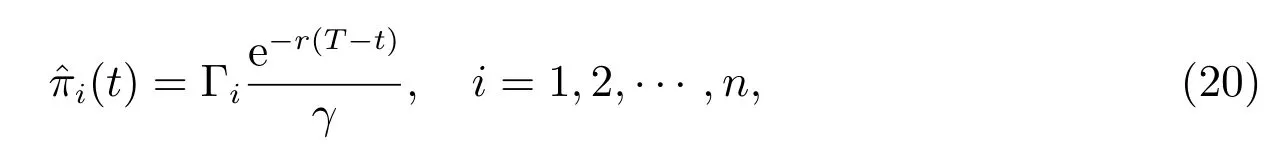
這里Γi定義為

利用定理1 和引理1 至引理3，我們得以得到問題(5)的解.

定理2對于問題(5)，最優時間一致的再保險策略為

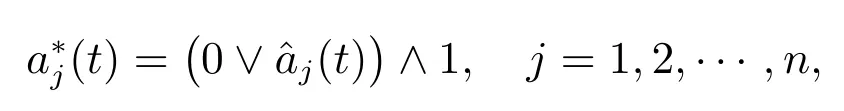
最優時間一致的投資策略為

最優值函數為

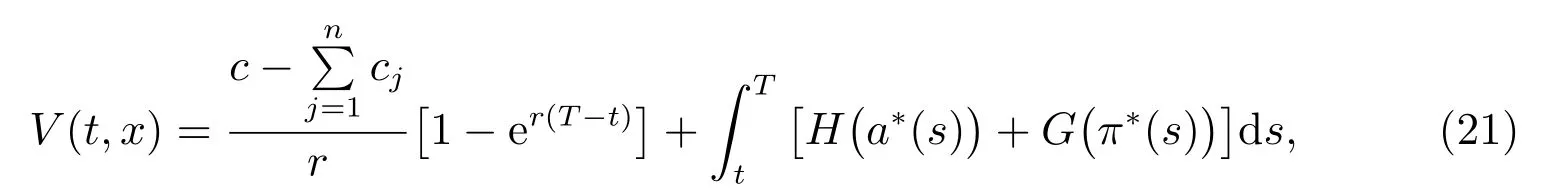
證明 由引理1，V(t，x)和h(t，x)關于t 求一階偏導數，關于x 求一階和二階偏導數，可以得到

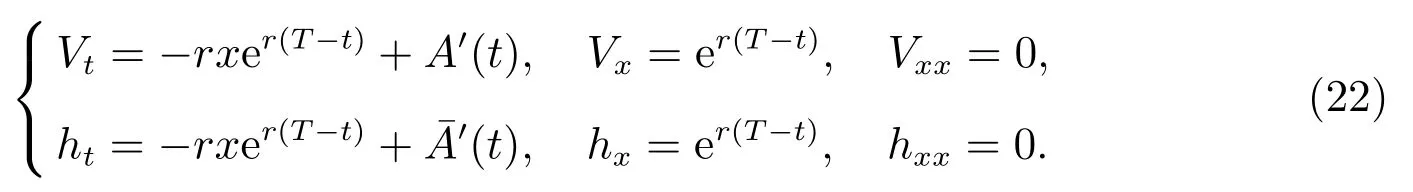
把(11)，(12)式和(22)式代入(8)式，化簡后得到

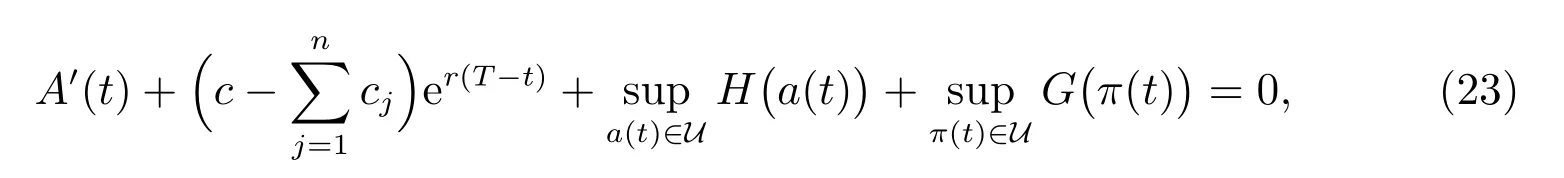
這里

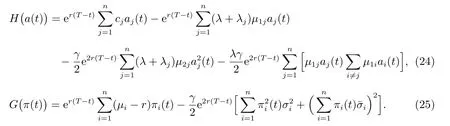
聯合引理2 和定理2，我們容易得到，保險公司對于保險業務j 是否采取再保險，以及把多少比例的保險業務分給再保險公司的準則.

性質1假設保險公司經營n 類保險業務，當

保險公司會對保險業務j 全部進行再保險；當

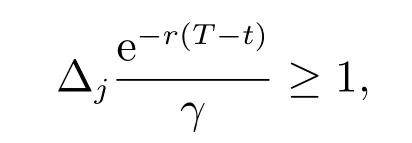
保險公司不會對保險業務j 進行再保險；當

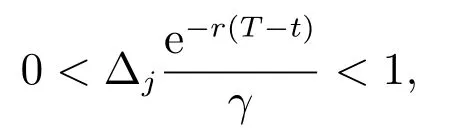
保險公司會對保險業務j 部分進行再保險，即把

比例的保險業務j 分給再保險公司.

聯合引理3 和定理2，我們容易可以得到保險公司是否在風險資產i 上投資的準則.

性質2當金融市場存在n 種風險資產時，只有當Γi＞0，才會在風險資產i 上進行投資.

下面，給出我們模型的兩種特殊情況.

如果保險公司只從事一類保險業務，不妨假設只從事保險業務1，由定理2 可以得到下面的推論1.

推論1如果保險公司只從事保險業務1，則保險公司最優時間一致的再保險策略為

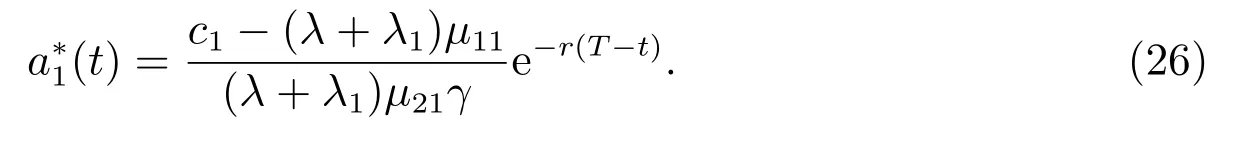
如果保險公司只投資1 個風險資產，不妨假設只投資風險資產1，由(20)式和定理2 可以得到下面的推論2.

推論2如果保險公司只投資風險資產1，則保險公司最優時間一致的投資策略為

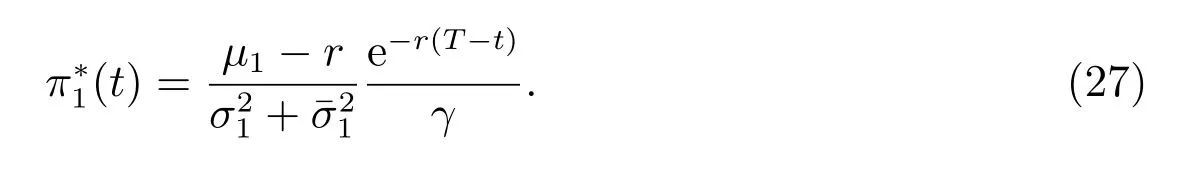
5 敏感性分析

本節我們通過一些數值實驗，分析模型參數對最優時間一致的再保險策略和投資策略的影響.不失一般性，假設保險公司從事兩類保險業務，在兩個風險資產上投資.下文中，如果沒有特殊說明，模型參數由表1 給出.

表1 數值實驗中模型參數的取值

接下來，我們首先分析模型參數對最優時間一致的再保險策略的影響.

保險公司會把保險業務1(或保險業務2)全部留給自己，而不采取再保險.

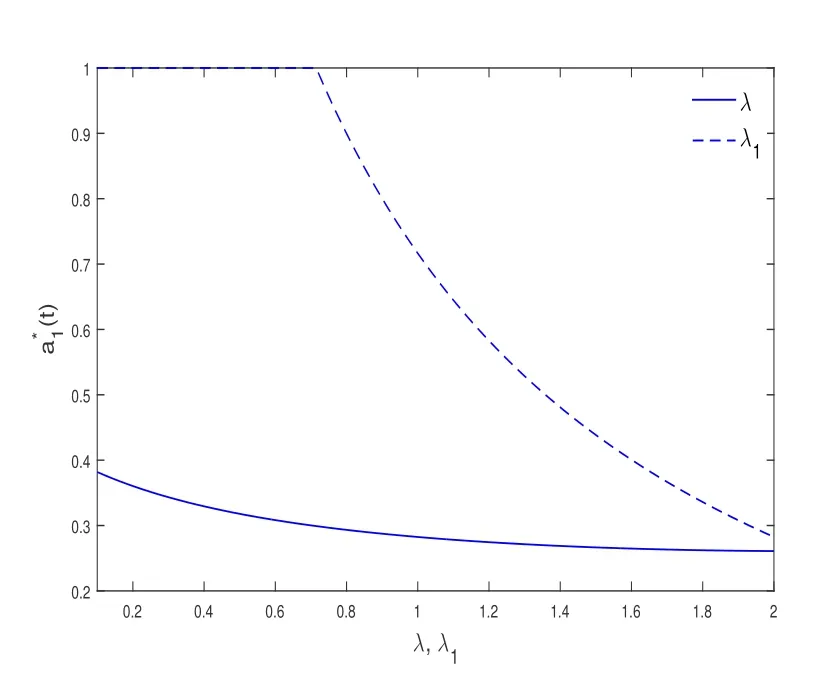
圖1 λ 和λ1 對a*1(t)的影響

圖2 λ 和λ2 對a*2(t)的影響

下面，分析風險資產的價格參數對最優時間一致的投資策略的影響.

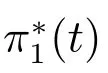
圖3 μ1 和μ2 對的影響

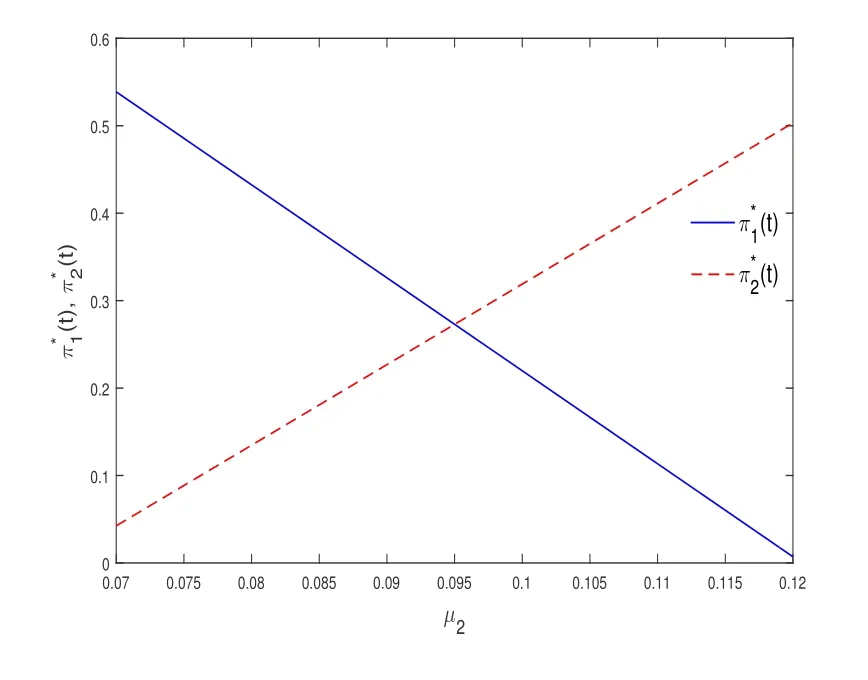
圖4 μ1 和μ2 對的影響

最終，圖5 和圖6 解釋了風險資產的波動率σ1和σ2對π*1(t)和π*2(t)的影響.從圖5 可以看出，隨著σ1增加，保險公司減少在風險資產1 上的投資資金，增加在風險資產2 上的投資資金.這是因為，隨著σ1的增加，風險資產1 的投資風險增加，而風險資產2 的投資風險不變，保險公司為了規避風險，逐漸轉移到在風險資產2 上進行投資.圖6 闡述了相似的經濟意義.

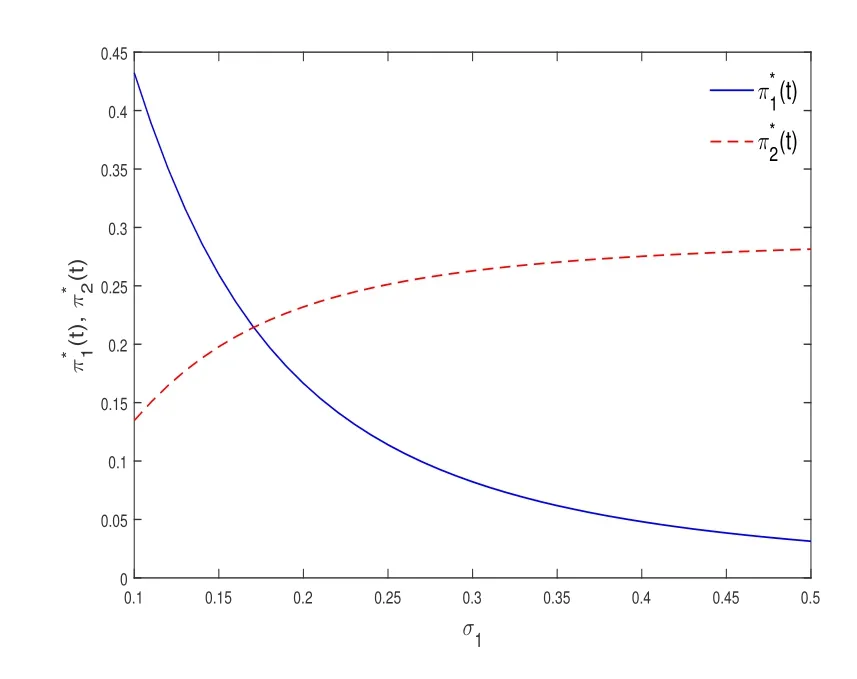
圖5 σ1 和σ2 對的影響

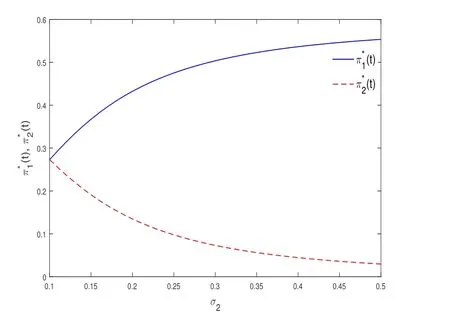
圖6 σ1 和σ2 對的影響

進一步分析圖3 至圖6，我們會看到，當只有一個風險資產的平均回報率增加時，保險公司會逐漸把資金集中投資在這個風險資產上；當只有一個風險資產的波動率增加時，保險公司會逐漸把資金集中投資在其它風險資產上.根據性質2，我們可以判斷保險公司是否在某個風險資產上進行投資.

6 總結

本文在保險公司經營n 類相依保險業務下，研究了最優時間一致的再保險和投資問題.保險公司的目標是在時間不一致的均值-方差問題中，求得時間一致的再保險和投資策略.基于博弈論的思想，利用隨機控制和隨機動態規劃技術，我們建立了推廣的HJB 方程，通過求解推廣的HJB 方程得到了時間一致的再保險和投資策略以及相應值函數的顯式解.最后，通過數值實驗，解釋了模型參數對最優時間一致再保險和投資策略的影響.通過理論分析和數值實驗，我們有以下發現：

(i) 我們得到了保險公司對于每類保險業務是否進行再保險，以及把多少比例的保險業務進行再保險的準則；

(ii) 與自身的理賠因素相比，當保險業務之間的理賠相依性增加時，保險公司會保留更少的保險業務；

(iii) 我們得到了保險公司是否在某個風險資產上投資的準則.