1 種寬馬赫數二元超聲速進氣道性能快速計算方法
劉 雨,王定奇,謝旅榮
(1.中國飛行試驗研究院,西安710089;2.南京航空航天大學能源與動力學院,南京210016)
0 引言
進氣道是現代高性能超聲速飛行器推進裝置的重要部件,對于1 個工作在寬馬赫數范圍內的超聲速飛行器,幾何型面固定的進氣道無法滿足不同飛行速度下的性能需求[1-4],這種能力不匹配問題會隨著飛行器速度的提高而愈發突出。因此設計人員開始考慮寬馬赫數范圍內性能表現更優的變幾何進氣道方案[5-7]。通常采用的方案是根據相關準則設計不同的進氣道壓縮楔角調節規律[8-10]。美國的X-43A 飛行器的部分唇罩可以轉動來匹配不同的飛行馬赫數[11];日本JAXA研究的TBCC 發動機采用了1 個第2 級壓縮楔面可轉動的二元變幾何進氣道方案[12];金志光等[13]研究了唇口可以轉動調節的變幾何進氣道設計方案,可以實現不需要附面層抽吸裝置即可在唇口開啟過程中實現接力點起動。但由于設計參數多、參數調節范圍大等因素,想要通過計算流體技術來初步設計進氣道幾何型面和參數調節方案要花費巨大的計算資源和時間。盡管可以對模型進行簡化并且應用自動化設計[14-15],仍然存在耗時巨大、過程復雜的問題,不利于變幾何進氣道型面調節方案設計和初步性能計算。因此國內外研究者都開展了不同的進氣道性能快速計算方法,來滿足變幾何進氣道設計快速迭代的需求。JOHN[16]結合彈用超聲速進氣道的數值模擬和試驗結果,提出了超聲速進氣道工作在臨界狀態時,擴張段內黏性損失的的快速估算方法,應用于進氣道擴張段快速設計;Bruce 等[17]在矩形進氣道擴張段內激波-邊界層干擾性能的研究基礎上,總結了偽激波串和正激波對氣流壓縮的規律,提出了擴張段內偽激波串性能快速計算方法,并應用于超聲速進氣道超臨界狀態性能快速計算中;張紅軍等[18]提出了采用進氣道超聲速段的數值計算與亞聲速段的工程計算相結合的方法解決常規超聲速進氣道臨界性能計算中需要不斷試湊反壓的問題,極大提高了優化過程中進氣道臨界性能的計算效率;關祥東等[19]通過0 維流動分析,提出了1 種基于流管收縮比計算臨界總壓恢復系數的理論公式,并結合大量風洞試驗和數值模擬數據對理論分析進行實證研究,獲得了臨界總壓恢復系數隨流量系數與來流馬赫數對應的流函數之積呈正相關的變化規律。
本文對二元超聲速進氣道流場結構進行分析,建立進氣道全流場的0 維性能快速計算方法,利用1 個二元超聲速進氣道對計算方法進行了仿真校驗,并將該方法應用于變幾何二元進氣道方案設計中。
1 二元超聲速進氣道性能計算方法
1.1 進氣道流場結構分析
混壓式二元進氣道流場結構如圖1 所示。首先是在進氣道前體楔板產生的2 道斜激波,其次進氣道唇罩內壁面與來流不平行也會產生1 道斜激波,這道斜激波會在擴張段內不斷反射,最終形成結尾激波串。超聲速來流經過這3 道斜激波和結尾激波系的壓縮增壓后,其壓力與燃燒室入口壓力相等。
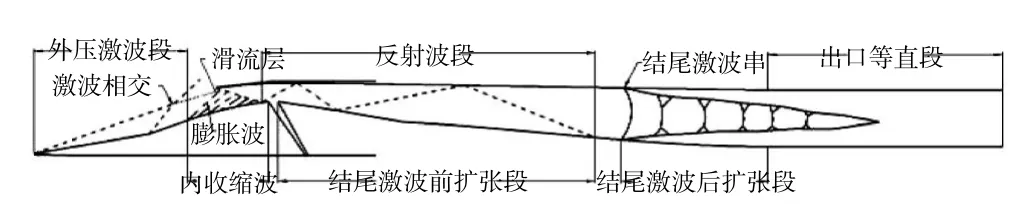
圖1 混壓式二元超聲速進氣道流場結構
1.2 進氣道外壓縮段參數計算
1.2.1 無黏激波計算
氣流流經前體楔面產生2 道斜激波時,波后馬赫數、總/靜壓比等參數可以通過求解斜激波公式獲得。正/斜激波理論公式為
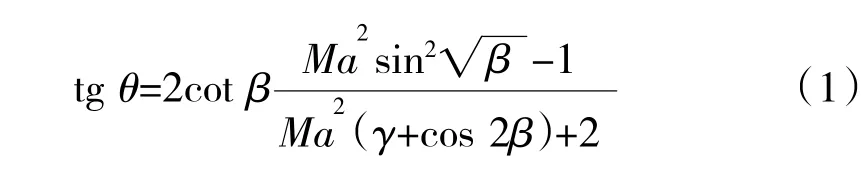
式中:θ 為激波角;β 為氣流偏轉角;Ma 為馬赫數。
1.2.2 邊界層修正方法
在氣體黏性作用下,進氣道前體上存在1 層附面層。平板附面層厚度估算為

式中:δ 為附面層厚度;x 為到平板起點的距離;Rex為當地雷諾數。
可以看到附面層厚度增長率隨著到平板起點距離的增加而減小。本文從平板起點取長度L,利用等效三角形求得斜激波修正轉角,如圖2 所示。
即有
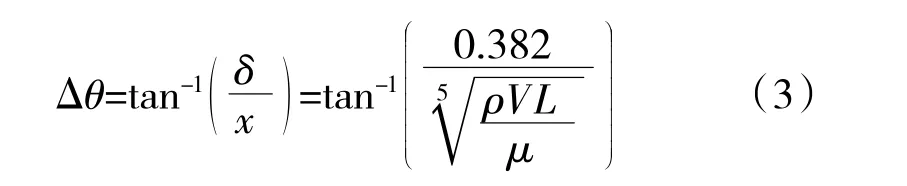
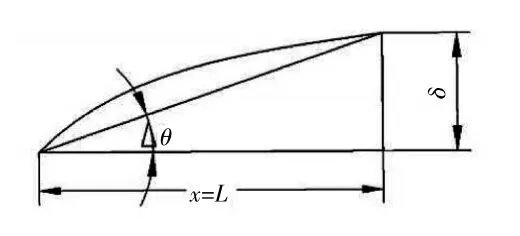
圖2 等效修正角度
式中:L 為楔板長度;V、ρ 分別為未修正的激波后參數。
另外,內壓縮通道入口處的總附面層厚度是2 道壓縮楔面的附面層厚度之和。
利用等效修正轉角修正后的斜激波理論公式為
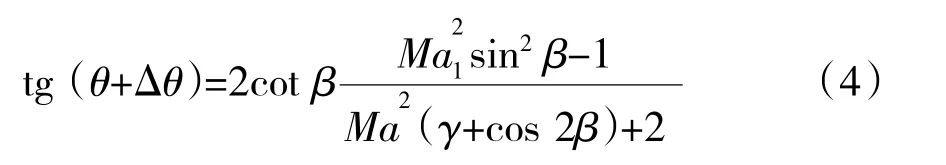
1.3 內收縮段參數計算
在進氣道肩部圓弧過渡段處會產生膨脹波扇,將其簡化為1 道P-M 膨脹波求解。利用連續方程求解內收縮段和擴張段進、出口參數。
當進氣道在高于設計馬赫數時工作,2 道外壓斜激波會在進氣道唇口前方交匯,在交匯點上方形成1道更強的激波,由于交匯點上下流場不同,形成滑流層。利用同側激波相交規律求解滑流層上下氣流參數,然后利用質量加權平均方法求解得到內收縮段的入口氣流參數。
進氣道內收縮段的氣流同時受到膨脹波和內收縮壁面的作用,本文采用簡單的平均方法對這2 種作用進行簡化。計算出第2 道斜激波后氣流通過膨脹波扇和內收縮通道后的參數平均值,將其作為唇口處第3 道斜激波前氣流的參數。
1.4 壓縮段壁面黏性損失修正
根據文獻[20],在來流馬赫數低于5.0 時,對總壓恢復系數進行黏性損失修正
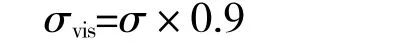
式中:σvis為修正后的總壓恢復系數;σ 為計算得到的無黏總壓損失系數。
1.5 擴張段性能計算
1.5.1 臨界狀態進氣道擴張段參數計算
當進氣道處于臨界工作狀態時,其唇口內流場可以簡化為進入唇口外壓縮面斜激波的反射激波+喉道處的正激波+唇罩內壁面斜激波。
在臨界工作狀態下擴張段的黏性損失估算[16]為
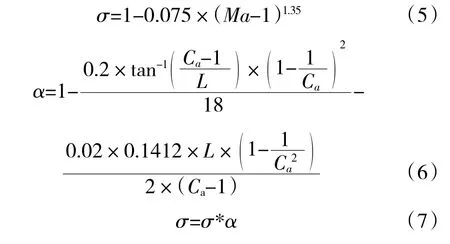
式中:Ca為擴張比;L 為擴張段長度/入口高度;α、σ*分別為修正系數和擴張段內總壓恢復系數。
1.5.2 超臨界狀態進氣道擴張段參數計算
當進氣道處于超臨界工作狀態時,由于激波/邊界層干擾,使得擴張段內出現“偽激波”形式的結尾激波串。計算進氣道性能時,以氣流經過擴張段一系列反射激波后的參數作為偽激波前氣流參數。氣流經過1 道正激波的增壓比約為經過偽激波后增壓比的1.25 倍[17]。根據這一規律便可以通過流量守恒方程求解偽激波后的氣流參數。

式中:Manor、Pnor和Mashocks、Pshocks分別為正激波后的馬赫數、靜壓和偽激波后的馬赫數、靜壓;A 為擴張段偽激波處截面積;k 為空氣比熱比;R 為氣體常數;T*為氣流總溫。
2 進氣道幾何模型
設計了定幾何二元超聲速進氣道,如圖3 所示。其設計馬赫數為3.7,工作馬赫數范圍為2.5~4.5。進氣道喉道高度Hth=41.5 mm,擴張段中心線根據前緩后急的變化規律設計,楔面及唇罩前緣采用半徑為0.3、0.2 mm 的鈍化處理。
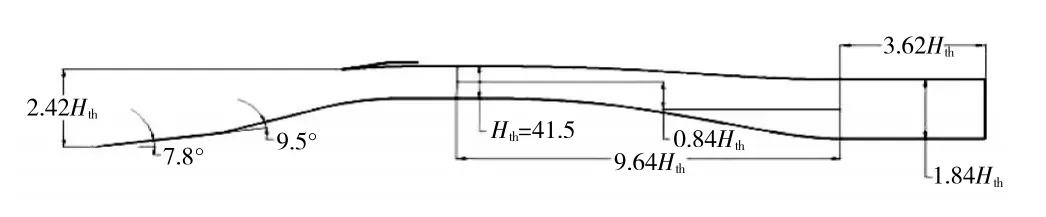
圖3 定幾何進氣道幾何型面
3 程序驗證
3.1 數值仿真方法校驗
3.1.1 數值仿真方法
采用商用仿真軟件Fluent 對進氣道流場進行數值模擬,采用標準 湍流模型對邊界層網格進行加密。采用結構化網格,數量約為12 萬。仿真計算來流條件見表1。

表1 進氣道來流參數
3.1.2 算例驗證
文獻[21]中的2 波系混壓式進氣道試驗模型如圖4 所示。利用其試驗數據對本文采用的數值仿真方法進行校驗。試驗條件為:來流馬赫數為4.03,來流總壓為1378 kPa,來流靜壓為8.721 kPa,總溫為1273.85 K,進氣道出口保持通流。
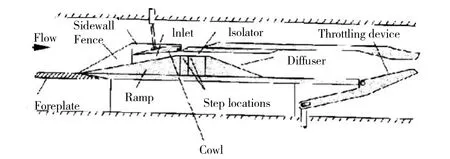
圖4 超燃沖壓發動機進氣道構型[16]
數值仿真得到的進氣道下壁面壓力值與試驗值的對比結果如圖5 所示。二者的壁面沿程壓力分布吻合程度較高,捕獲到的激波位置相近。說明本文采用的數值仿真方法計算結果是準確的。
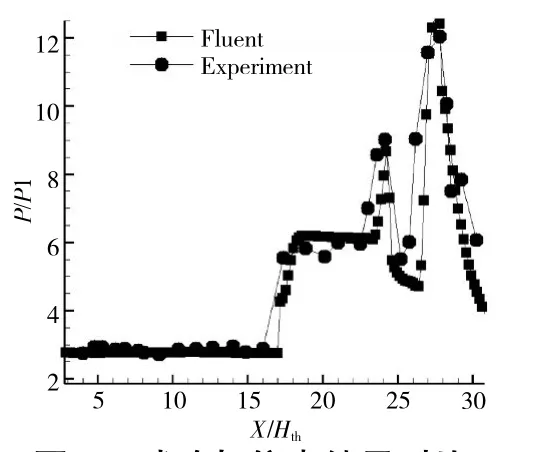
圖5 試驗與仿真結果對比
3.2 定幾何進氣道結果對比
編制了進氣道0 維性能計算程序,針對前文設計的定幾何進氣道,利用數值模擬和程序分別計算了進氣道臨界狀態的喉道馬赫數、流量系數和總壓恢復系數,如圖6 所示。
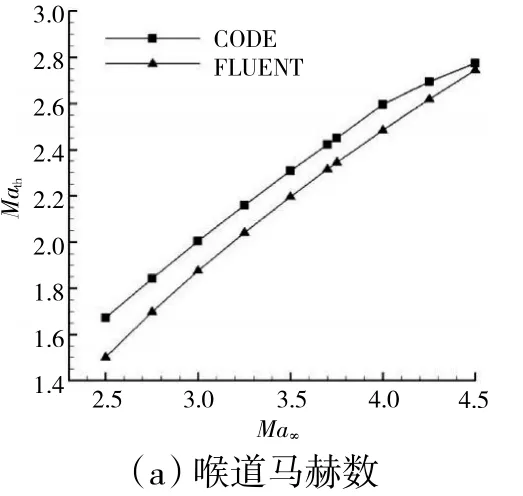

圖6 程序與仿真計算結果對比
參考第3.1 節數值方法校驗結果可知,Fluent 軟件仿真結果可以準確反映進氣道流場特征及性能參數,因此采用仿真結果做標尺來檢驗編制的進氣道性能快速計算程序結果。對比發現程序計算的進氣道喉道馬赫數和流量系數均略大于Fluent 軟件的仿真結果。這可能是因為程序較低地估算了黏性損失和附面層發展厚度,并且沒有考慮前體壓縮面和唇罩前緣的鈍化處理效應,從而導致程序計算得到的臨界總壓恢復系數偏小。但是誤差在5%以內,因此該程序可以用來初步快速估算進氣道的性能。
程序計算和數值仿真得到的來流馬赫數為3.25和3.50 時,進氣道在超臨界工作狀態時出口總壓恢復系數隨出口壓比(進氣道出口靜壓/來流靜壓)的變化如圖7 所示。從圖中可見,隨著出口壓比的增大,進氣道結尾激波串前移,激波串前馬赫數降低,結尾激波損失減小,進氣道出口總壓恢復系數增大。第1.4 節擴張段激波串的處理方法是較合理的,并且進氣道出口壓比越大、越接近臨界工作狀態時,該計算方法的誤差越小。
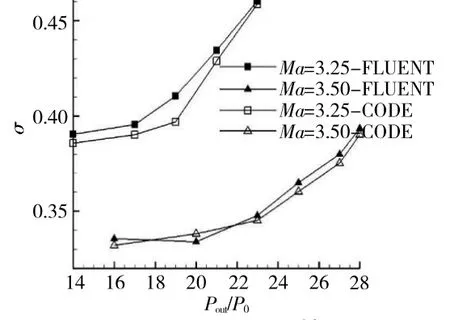
圖7 程序與仿真計算超臨界狀態總壓恢復系數
3.3 變幾何進氣道初步設計及結果對比
為了改善定幾何進氣道工作在低馬赫數和高馬赫數時對應的流量系數和臨界總壓恢復系數偏小的問題,針對前文的定幾何進氣道提出1 種第2 級壓縮楔面角度可調的變幾何方案,如圖8 所示。

圖8 變幾何進氣道
利用前文編制的程序計算進氣道性能,并對變幾何進氣道型面調節規律進行初步設計,依照2 點原則篩選調節規律:(1)前體壓縮楔面的第2 道斜激波在大的工作馬赫數范圍內封口;(2)進氣道的綜合性能較高。這樣設計的目的是在整個工作范圍內具有較大臨界總壓恢復系數和流量系數。尤其當進氣道工作在設計馬赫數之上時,外壓楔面第2 道斜激波封口能改善高馬赫數時定幾何進氣道前體斜激波進入內通道,造成較大氣流分離的現象。
將變幾何進氣道的第1 級壓縮角度δ1固定為7.8°。δ2、δ3按第2 道外壓斜激波封口原則設計時,結果見表2。進氣道性能參數變化如圖9 所示。將變幾何進氣道的第,2 級楔面壓縮角度和唇罩氣流壓縮角度的調節規律記為variable-1。從圖9(a)中可見,程序計算結果顯示在低馬赫數variable-1 方案進氣道的臨界總壓恢復系數偏小。所以重新設定起始第2 級壓縮角度為4.01°,從來流馬赫數為3.0 開始,第2、3級壓縮角度按照表2 中所示的規律進行調節,記為variable-2,程序計算結果顯示在來流馬赫數為2.5 時的進氣道臨界總壓恢復系數顯著增大。同時,從圖9(b)中可見,在低馬赫數時variable-2 方案的流量系數同樣明顯超過定幾何進氣道,說明此方案滿足了最初所提的要求。
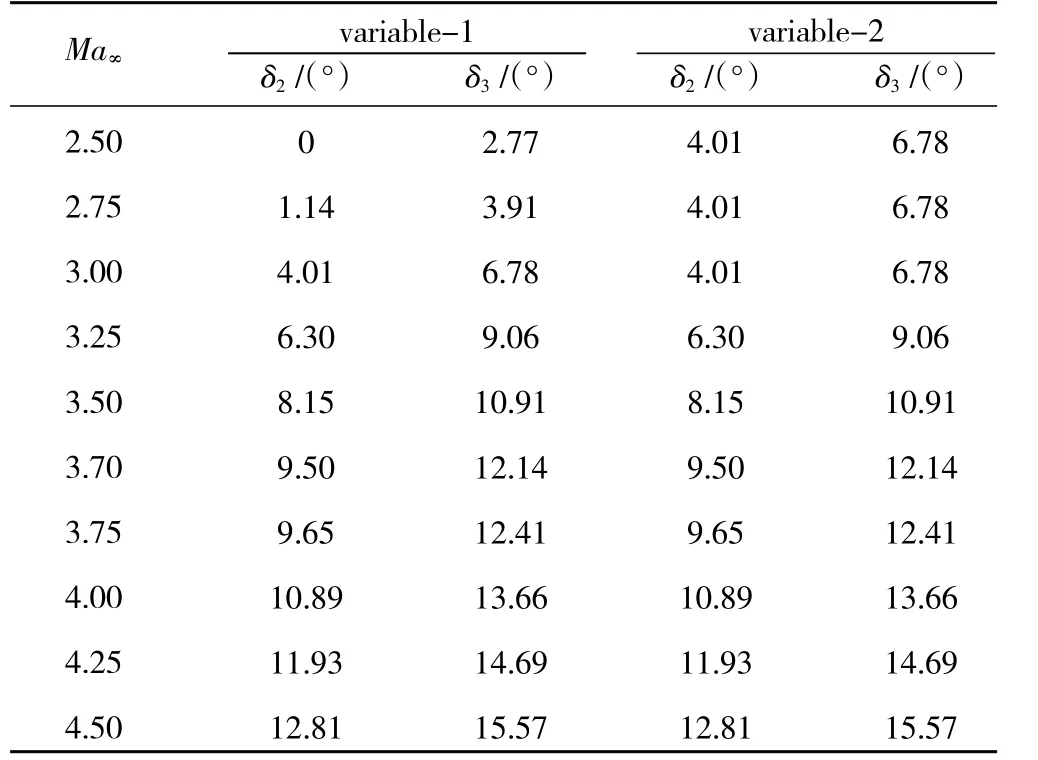
表2 變幾何進氣道楔面調節規律
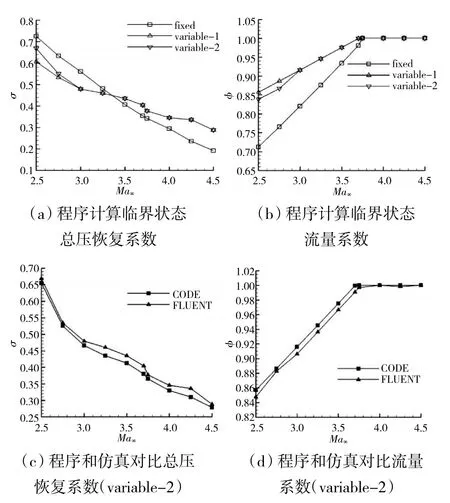
圖9 進氣道性能參數變化
隨后采用數值仿真方法對variable-2 方案的進氣道臨界狀態性能進行計算,并與程序計算結果進行對比。從圖9(c)、(d)中可見,處于臨界狀態時variable-2 方案變幾何進氣道流量系數和總壓恢復系數隨來流馬赫數的變化,程序計算的性能參數變化趨勢與仿真結果的基本一致,但是總壓恢復系數的誤差要比計算定幾何時的大,其原因可能是變幾何進氣道在各工作馬赫數下型面變化較大,通道內流場更復雜的緣故。但是誤差小于8%,在可接受范圍內,所以該方法可用于楔面調節的變幾何進氣道型面的初步設計和性能快速計算。
3.4 誤差分析
本文提出的進氣道性能快速計算方法的誤差主要有2 方面:(1)附面層黏性損失及厚度估算誤差;(2)進氣道擴張段內偽激波在超臨界狀態下與正激波相差較遠,導致此時誤差較大。程序計算的定/變幾何進氣道性能參數和Fluent 仿真計算的性能參數的誤差比較見表3。從表中可見,流量系數的誤差較小,在3%以內,這是因為進氣道外壓激波系流場比較簡單。但是臨界總壓恢復系數誤差較大,最大誤差達到8.01%,而且在來流馬赫數為3.50 左右時計算出的變幾何進氣道臨界總壓恢復系數誤差較大,分析是因此時進氣道楔板調節幅度較大造成的。
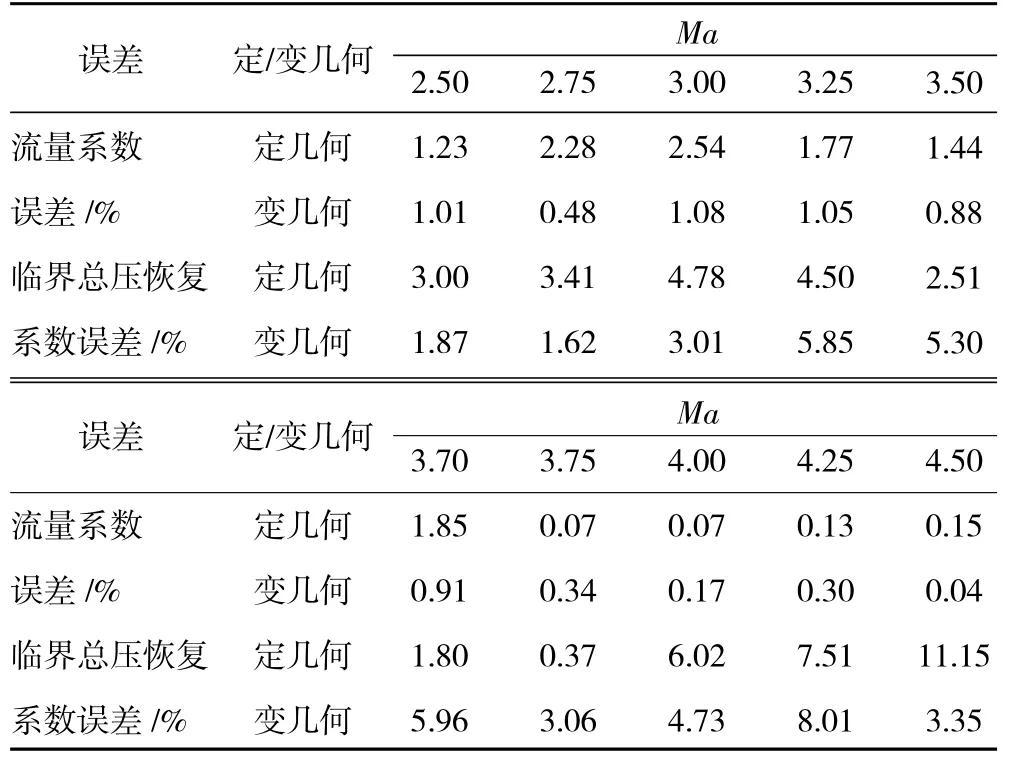
表3 進氣道性能快速計算方法誤差變化規律
4 結論
本文提出了1 種二元超聲速進氣道性能快速計算方法,以1 個工作馬赫數范圍為2.5~4.5 的進氣道為算例,將程序計算結果與CFD 結果進行比對,得出以下結論:
(1)本方法是在分析進氣道內流場結構的基礎上,利用激波理論、黏性修正和工程經驗修正建立的,對于寬馬赫數工作的二元超聲速進氣道流量系數和臨界總壓恢復系數等性能參數估算有較高精度;
(2)通過對進氣道擴張段內偽激波串進行簡化處理后,該方法也可用于估算進氣道的超臨界狀態性能;
(3)本文的性能估算方法計算速度快,精度較高,可用于變幾何二元進氣道楔面調節規律的初步型面選型設計和性能計算。

