彈性支承振動應力信號降噪方法及其性能對比

邊 杰，鄭錦妮，陳亞農，徐友良，2

（1.中國航發湖南動力機械研究所；2.中國航空發動機集團航空發動機振動技術重點實驗室；3.直升機傳動技術國防科技重點實驗室：湖南株洲412002）

0 引言

彈性支承作為1 種支承結構，普遍用于中小型航空發動機的轉子支承中，可用于調節轉子的臨界轉速且具有減振降幅的功能。為了保證轉子安全運行，在彈性支承的彈條上粘貼應變片，通過測量彈性支承振動應力信號監測轉子的振動狀態。彈性支承振動應力信號常受其他信號干擾，由于噪聲信號的存在，使轉子固有的特征信息反而不明顯。為此，通常在對彈性支承振動應力信號進行頻譜分析前作降噪處理，減小噪聲對彈性支承振動應力信號的影響。

目前，基于時頻信號分解方法的信號降噪技術的快速發展，建立了如小波變換（Wavelet Transform，WT）[1]、經驗模態分解（Empirical Mode Decomposition，EMD）[2]、集合經驗模態分解（Ensemble Empirical Mode Decomposition，EEMD）[3-4]以及互補集合經驗模態分解（Complete Ensemble Empirical Mode Decomposition，CEEMD）和排列熵的小波閾值[5]的降噪方法等。小波降噪方法基于小波變換或小波閾值降噪，對于噪聲頻帶和有用信號相互分離時的確定性噪聲能基本降噪；但在噪聲頻帶和有用信號相互疊加時，降噪效果不明顯[6]。無論EMD、EEMD 還是CEEMD 降噪方法，都是基于EMD、EEMD 和CEEMD 分解。受這些方法自身的影響，如EMD 分解不穩定、存在模態混疊現象，導致某一固有模態分量中包含不同尺度的信號或相似尺度信號存在于不同模態分量中[7]。EEMD 和CEEMD降噪方法在原始信號中加入了白噪聲，使得分解結果受到殘余噪聲的影響。

近年來，在時頻信號分解方法研究成果的基礎上，本文結合樣本熵（Sample Entropy，SampEn）、奇異值分解（Singular Value Decomposition，SVD）及峭度系數等，提出用于彈性支承振動應力信號降噪的方法，并對幾種方法的降噪效果和計算效率進行對比，得到1 種用于彈性支承振動應力信號降噪的最有效方法。

1 時頻信號分解方法

1.1 EMD 方法

EMD 方法是1 種自適應的信號分解方法，對于信號x（t），EMD 的分解步驟如下[8]：

（1）使用3 次樣條曲線分別連接相鄰的局部極值點，得到上、下包絡線。

（2）將上、下包絡進行平均，得到均值m（t）。

（3）計算h（t）=x（t）-m（t）。

（4）對h（t）重復步驟（1）～（3），直至m（t）接近于0。則h（t）為IMF 分量，記為c（t）。

（5）計算余項r（t）=x（t）-c（t）。

（6）將r（t）替代x（t）重復步驟（1）～（5），得到下一個IMF 分量和余項。

因此，信號x（t）經EMD 分解后進行重構為

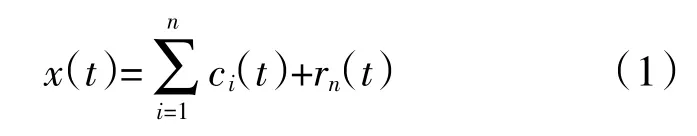
式中：ci（t）為第i 個IMF 分量；rn（t）為第n 個余項。

1.2 CEEMDAN 方法

對于給定信號x [n]，由EMD 方法分解得到第階模態定義為Ej（·），自適應噪聲完備集成經驗模態分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN）的分解過程如下[9]：

（1）使用EMD 方法對信號x[n]+ε0ωi（n）進行I 次試驗，分解得到第1 個模態為

（2）在第1 階段（k=1），計算第1 個殘量信號

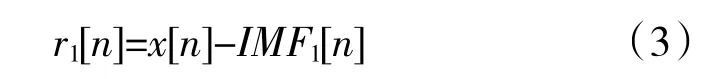
（3）在i 次試驗中，對信號r1[n]+ε1E1（ωi（n）），（i=1,…,I）進行分解，直到得到第1 個EMD 模態分量為止，定義第2 個模態分量為

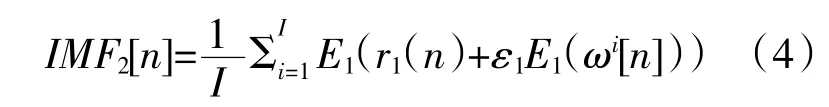
（4）當k=2,…，K 階段時，計算第k 個殘量信號

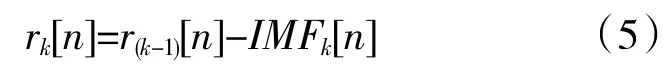
（5）同步驟（3），計算得到第k+1 個模態分量為

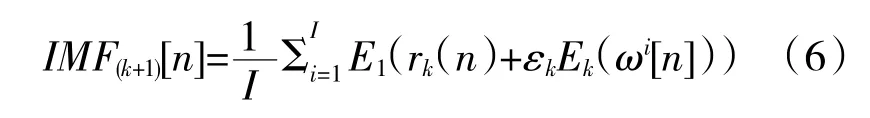
（6）對于下一個k 階段，重復步驟（4），直至殘量信號不能再分解為止（極值點數不超過2）。

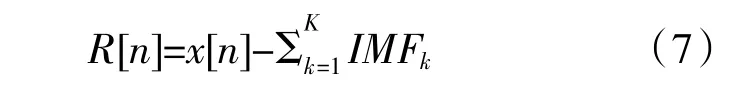
式中：K 為總的模態分量數。

則最終信號x[n]表示為

1.3 LMD 方法

局部均值分解（Local Mean Decomposition，LMD）方法將調制信號分解成1 組乘積函數（PFs），每個乘積函數是1 個包絡信號和調頻信號的乘積。LMD 分解算法簡要介紹如下[10]。

對于給定信號x（t），設初值r0（t）=x（t），i=0。

（1）設c0（t）=ri（t），j=0。

（2）識別極值點cj（t），采用2 個相鄰極值點計算局部均值和包絡為mi=（cj（ti）+cj（ti+1））/2，ai=|cj（ti）-cj（ti+1）|/2。

（3）采用滑移平均方法對局部均值和局部包絡進行平滑，得到mj（t）和aj（t）。

（4）計算函數cj+1（t）=（cj（t）-mj（t））/aj（t）。

a.若a（jt）滿足設i=i+1，使

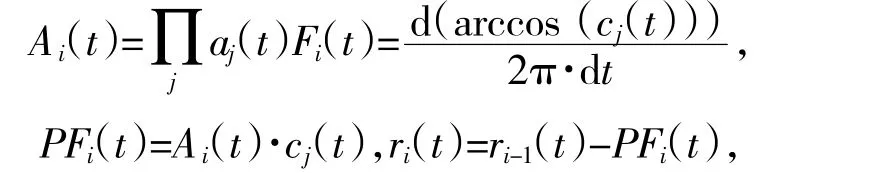
返回步驟（1）。

b.否則，設j=j+1，返回步驟（2）。

（5）重復步驟（1）～（4），直至不能再分解出新的PF 分量為止。

1.4 ITD 方法

固有時間尺度分解（Intrinsic Time-scale Decomposition，ITD）方法[11]將原始信號分解成1 組固有旋轉分量和1 個單調趨勢信號。設Xt為待分析信號，定義1 個基線提取算子L，使得從待分析信號中去掉該基線后剩下的余量信號成為1 個固有旋轉分量。1 次固有時間尺度分解式為

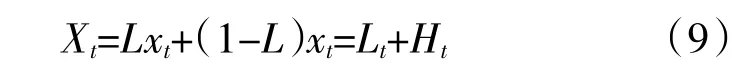
式中：Lt和Ht定義在[0，τk]區間；Xt定義在[0，τk+2]區間。在連續極值點[τk，τk+2]區間上定義Xt的基線提取因子L，即

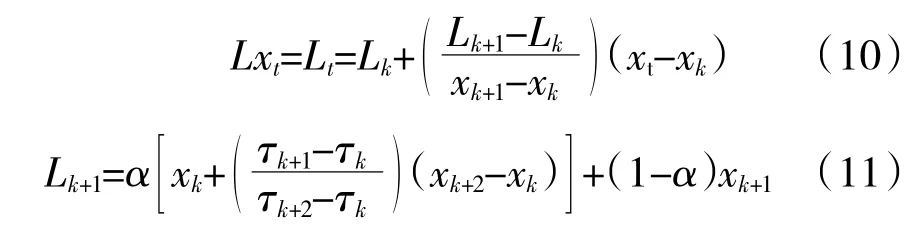
式中：α 為分解時的增益控制參數（0＜α＜1）；Lt保留了信號在各極值點處的單調性；Ht提取了各極值點之間疊加的局部高頻分量信號，即固有旋轉分量。

重復以上分解過程，可獲得一系列固有旋轉分量和1 個單調趨勢信號。

1.5 VMD 方法

變分模態分解（Variational Mode Decomposition，VMD）方法是在其變分模態框架內，獲得約束變分模態模型的最優解，完成信號的自適應分解。每個變分模態分量的中心頻率及帶寬在迭代求解中不斷更新，根據實際信號的頻域特性對信號頻帶進行自適應分解，最終得到1 組窄帶變分模態分量。假定原始信號x 被分解為k 個變分模態分量，則相應的約束變分模態模型為[12]

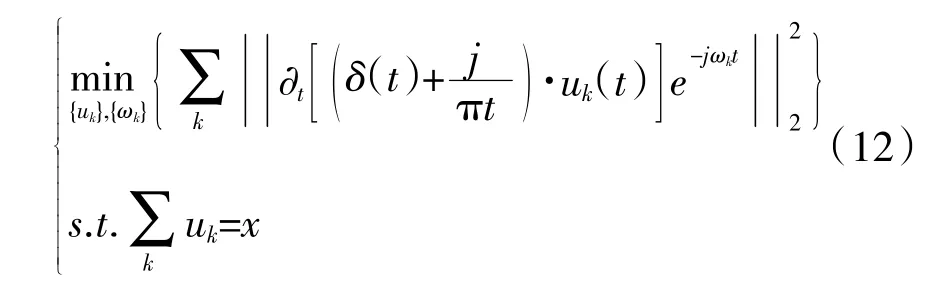
式中：uk、ωk分別為各變分模態分量和中心頻率。

為求解約束變分模態模型，在VMD 算法中引入2 次懲罰項α 和拉格郎日乘子λ。VMD 算法的具體實施過程如下：

（2）令n=n+1，執行循環過程；

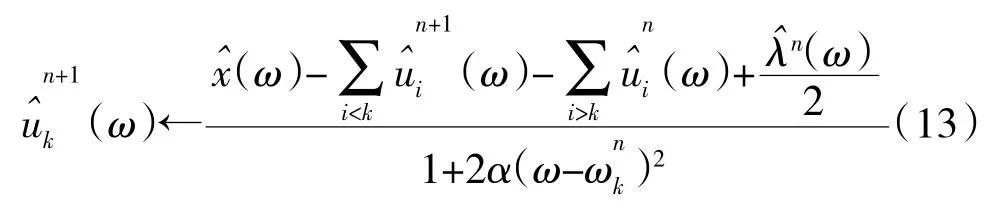
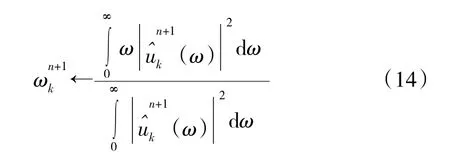
（4）更新λ

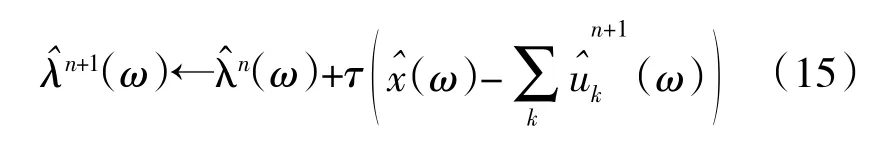
式中：τ 為噪聲容限參數。

2 信號降噪理論推導及具體實施方法

2.1 樣本熵

設時間序列x（1），x（2），…，x（N），計算該N 個時間序列樣本熵的步驟如下[13]：

（1）選定模式維數m，由原序列構成1 組m 維向量

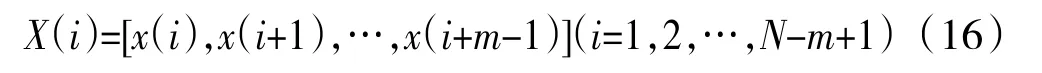
（2）定義X（i）和X（j）之間的距離

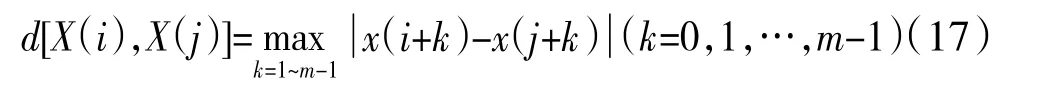
（3）設定閾值r，統計距離d[X（i），X（j）]不大于r的數，將此數與距離總數N-m+1 的比值記為

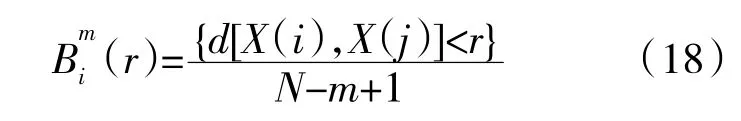
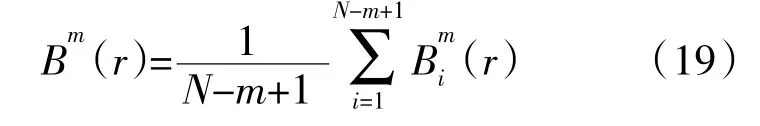
（4）重新選定模式維數m+1，構成1 組m+1維向量，重復步驟（1）～（3），得到Bm+1（r）

（5）此序列的樣本熵定義為

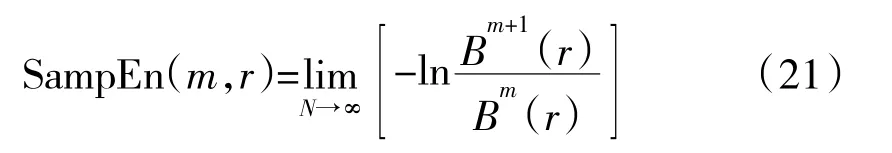
由定義可知，樣本熵的值與維數m 和閾值r 的取值有關。m 值越大計算時間越長，r 值越大時間序列的信息損失越大，反之噪聲影響越顯著。根據文獻[14]的研究，本文取m=2，r=0.15std。

2.2 奇異值分解

根據奇異值理論，任何p×q 階矩陣的奇異值分解（SVD）可表示為[15]

式中：U 為p×p 階正交矩陣；V 為q×q 階正交矩陣；Λ=diag（λ1，λ2，…，λk）為對角矩陣，k=min（p，q），λ1，λ2，…，λk為矩陣A 的奇異值并按降序排列。

矩陣的奇異值為矩陣的固有特征，具有很好的穩定性、比例不變性和旋轉不變性。

2.3 峭度系數

峭度系數表示故障形成的大幅值脈沖出現的概率。將脈沖響應與背景噪聲的差距加大以提高信噪比，峭度系數以脈沖響應幅值的4 次冪為判斷依據，使其準確度顯著提高。峭度系數的定義[16]為

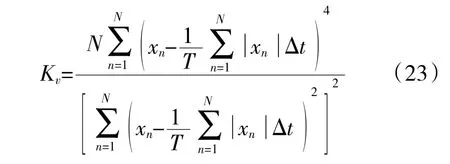
2.4 信號降噪具體實施方法

根據以上理論，彈性支承振動應力信號降噪具體實施方法如下：

（1）使用不同信號分解方法對彈性支承振動應力信號進行分解，得到k 個初始模態分量；

（2）計算所有初始模態分量的樣本熵，并對其歸一化處理，得到初始模態分量的歸一化樣本熵；

（3）設定歸一化樣本熵的閾值n，對所有大于閾值n 的初始模態分量進行SVD 降噪處理，而對不大于閾值n 的初始模態分量不作處理；

（4）計算SVD 降噪后初始模態分量的峭度系數，設定峭度系數的閾值為m；

（5）剔除峭度系數小于閾值m 的初始模態分量，保留不小于閾值m 的初始模態分量，并輸出最終的模態分量；

（6）將所有的模態分量重組成降噪信號，輸出降噪信號的信噪比、相關系數、均方誤差以及信號降噪處理時間。

信號降噪流程如圖1 所示。

3 彈性支承振動應力信號降噪應用

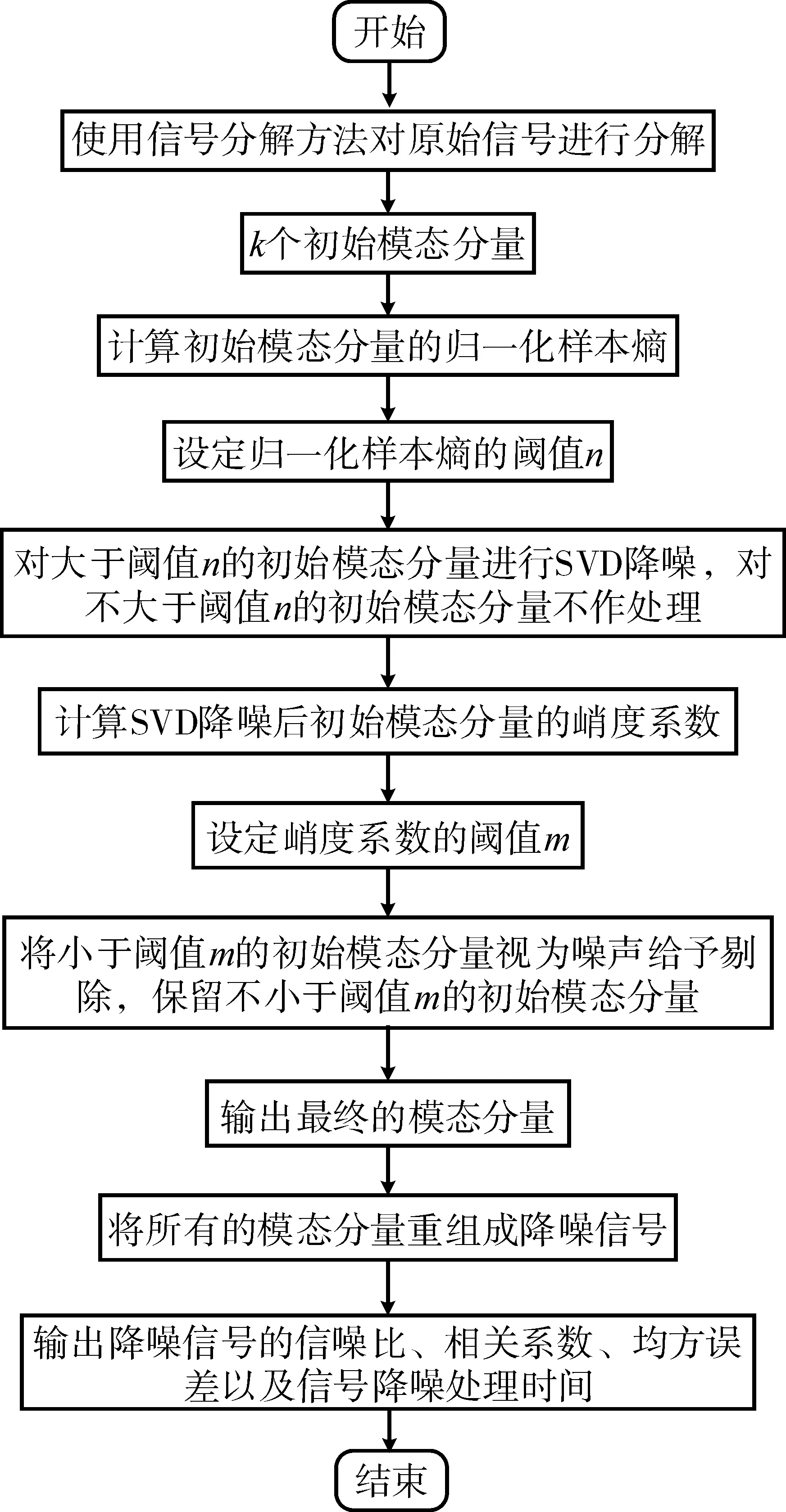
圖1 信號降噪流程

以某模擬轉子彈性支承振動應力信號為研究對象，采用不同信號分解方法對其進行信號降噪研究。彈性支承振動應力信號的采樣頻率為10 kHz，其時域波形及頻譜如圖2 所示。從圖中可見，彈性支承振動應力信號主要存在3 個頻率成分，分別為轉子基頻、2 倍頻和3 倍頻，其余幅值較低且頻帶較寬的雜亂譜線為噪聲干擾。由于噪聲干擾的存在，在信號波形中出現許多毛刺成分，不利于轉子信號特征的分辨，特別是早期的故障特征信號被覆蓋，如圖2（a）所示；在如圖2（b）所示的頻譜中，橫坐標階次定義為轉子基頻的N 倍，下同。

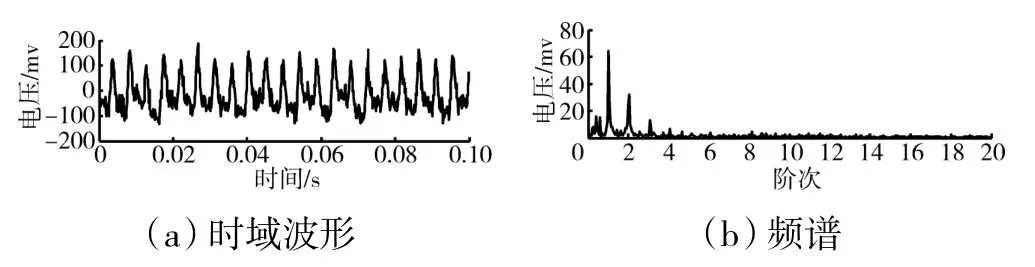
圖2 有噪聲干擾的彈性支承振動應力信號的時域波形及頻譜

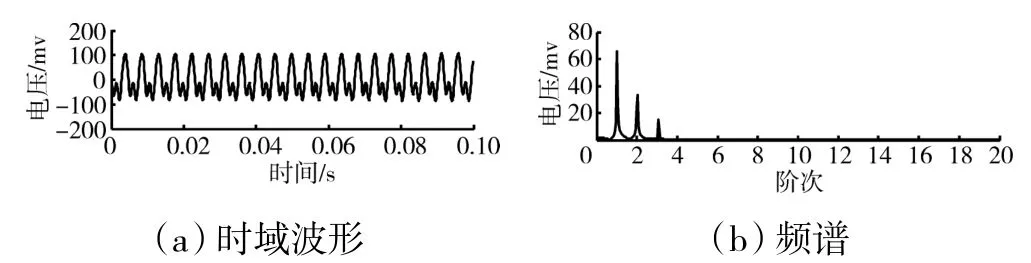
圖3 無噪聲干擾的彈性支承振動應力仿真信號的時域波形及頻譜

根據圖2 彈性支承振動應力信號的頻譜分析中的3 個主要頻率成分，仿真構造出無噪聲干擾的彈性支承振動應力信號，如圖3 所示。從圖中可見無噪聲干擾的彈性支承振動應力信號可用于不同降噪方法對該信號降噪效果的對比分析。與圖2 對比可見，在圖2 中有噪聲干擾的彈性支承振動應力信號的噪聲成分主要為低頻寬帶噪聲及寬頻帶的背景噪聲。

對于該彈性支承振動應力信號，根據信號降噪流程（圖1）對其進行降噪處理，其中歸一化樣本熵的閾值n＝0.5，峭度系數的閾值m＝5×105。

彈性支承振動應力信號經EMD-SampEn-SVD降噪后的時域波形和頻譜如圖4 所示。將圖4 與圖2、3 對比分析可見，EMD-SampEn-SVD 可降低較高頻帶上的背景噪聲，而對其他頻帶上的噪聲降低效果不明顯，特別是對低頻寬帶噪聲降低效果不佳。

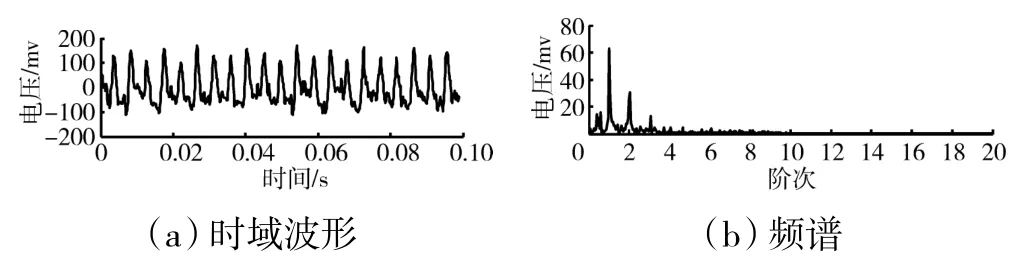
圖4 采用EMD-SampEn-SVD 降噪后彈性支承振動應力信號的時域波形及頻譜

采用CEEMDAN-SampEn-SVD 降噪后的彈性支承振動應力信號的時域波形與頻譜如圖5 所示。從圖中可見，在轉子基頻的6 倍頻以上的寬頻帶上，不存在背景噪聲成分，且低頻寬帶噪聲有一定程度削減。采用LMD-SampEn-SVD 方法降噪后彈性支承振動應力信號的時域波形及頻譜如圖6 所示。與圖5 相比，其低頻寬帶噪聲降低效果更佳，但在轉子基頻6倍頻以上，其降噪效果不如CEEMDAN-SampEn-SVD方法的。

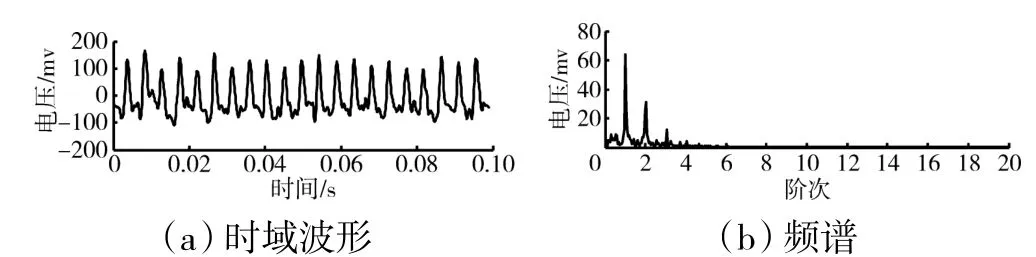
圖5 采用CEEMDAN-SampEn-SVD 降噪后彈性支承振動應力信號的時域波形與頻譜

圖6 采用LMD-SampEn-SVD 降噪后彈性支承振動應力信號的時域波形及頻譜

采用ITD-SampEn-SVD 降噪后彈性支承振動應力信號的時域波形及頻譜如圖7 所示。與圖2～6 對比可見，ITD-SampEn-SVD 方法在低頻寬帶噪聲及寬頻帶的背景噪聲上的降低效果均不佳。采用VMDSampEn-SVD 方法降噪后彈性支承振動應力信號的時域波形及頻譜如圖8 所示。通過對比圖2～8 可見，采用VMD-SampEn-SVD 方法能有效去除轉子基頻4倍頻以上的寬帶背景噪聲，同時對低頻寬帶噪聲的降低效果在所有降噪方法中是最好的。

圖7 采用ITD-SampEn-SVD 降噪后彈性支承振動應力信號的時域波形及頻譜

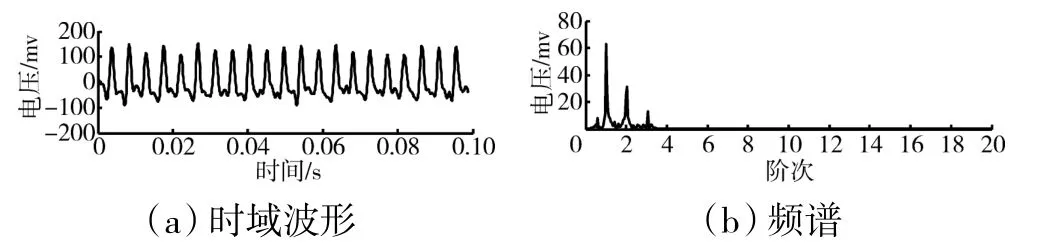
圖8 采用VMD-SampEn-SVD 降噪后彈性支承振動應力信號的時域波形及頻譜

為進一步對各種降噪方法進行性能（降噪效果和運算效率）對比，引入信噪比的概念。以信噪比RSN、相關系數和均方誤差作為降噪效果的評價指標

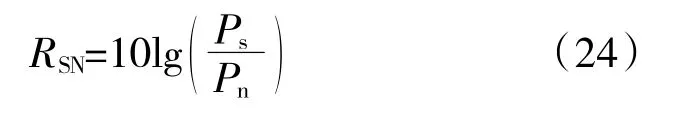
式中：Ps為純信號功率；Pn為噪聲功率。

相關系數用來衡量降噪后的信號與無噪聲干擾信號間的線性相關性，相關系數的絕對值越大，二者的相關性越大

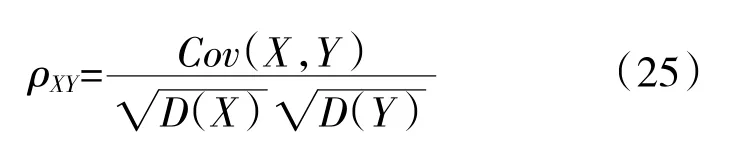
式中：Cov（X，Y）為X、Y 的協方差；D（X）、D（Y）分別為X、Y 的方差。

均方誤差EMS用來評價降噪后的信號與無噪聲干擾信號間的偏離程度，EMS值越小，說明降噪后信號的精確度越高

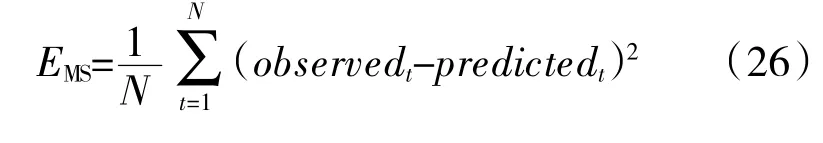
同時，以計算時間作為降噪方法的計算效率的評價指標。

5 種降噪方法的性能對比見表1。從表中可見，采用VMD-SampEn-SVD 方法降噪，彈性支承振動應力信號的信噪比為8.11 dB，相關系數為0.92，均方誤差為0.43，計算時間為18.04 s，在5 種降噪方法中的降噪效果最佳，計算效率也較高；而采用ITD-Samp-En-SVD 方法降噪，彈性支承振動應力信號的信噪比為5.68 dB，相關系數為0.88，均方誤差為1.63；計算時間最短為2.99 s，其降噪效果并不佳；采用CEEMDAN-SampEn-SVD 方法降噪，計算效率最低，計算時間為290.99 s，彈性支承振動應力信號的信噪比為6.43 dB，相關系數為0.90，均方誤差為0.98，降噪效果也不是最佳。綜上分析，VMD-SampEn-SVD 方法是5 種方法中最適用于彈性支承振動應力信號降噪的。

表1 5 種降噪方法的性能對比

4 結論

針對彈性支承振動應力信號，對5 種信號降噪方法進行性能對比，得出以下主要結論：

（1）本文介紹的信號降噪方法主要基于自適應的信號分解方法，并利用樣本熵、SVD 和峭度系數，通過設定閾值，篩出有效分量，去除噪聲成分。通過彈性支承振動應力信號的降噪研究，證明信號降噪方法是可行的。

（2）對彈性支承振動應力信號的降噪研究表明：在彈性支承應力信號的降噪效果上，VMD-Samp-En-SVD 方法最好，EMD-SampEn-SVD 方法最差；在計算時間上，ITD-SampEn-SVD 方法最短，而CEEM DAN-SampEn-SVD 方法最長。綜上所述，VMD-SampEn-SVD 方法是5 種方法中最適用于彈性支承振動應力信號降噪的方法。從5 種信號分解方法的理論及特點分析可知，此結論同樣可為其他測試信號的降噪處理提供參考。