1 種提高落壓比調節器可靠性的特征量裕度概率設計方法

高 帥，原莉莉，米東旭，侯曉鵬

（中國航發西安動力控制科技有限公司，西安710077）

0 引言

在產品全壽命周期內，通過逐步優化產品設計，可不斷提高產品可靠性[1-2]。可靠性提高技術始于1956年，最初由美國學者H.K.Weiss 提出可靠性提高模型的雛形；隨后Krasich M、Duane J T、Cox D R 等學者陸續提出多種可靠性提高模型[3]；20 世紀80 年代，美國先 后發 布了MIL-HDBK-189、IEC 61014、IEC 61164 等標準，中國也陸續推出適合中國國情的可靠性技術標準，有力地推進了可靠性技術的發展[4]。中國在載人航天、探月工程和國防科技等領域，已陸續開展了航天器機構的可靠性設計、試驗及其評估工作，取得了較好的效果[5-7]。

落壓比調節器是航空發動機的重要組成部分，其可靠性直接影響發動機的推力性能和安全性。某落壓比調節器多次出現控制失效，可靠性偏低，其主要原因是該關鍵元件反饋拉簧發生了疲勞斷裂。針對此問題，現有方法是提高反饋拉簧表面質量來防止疲勞斷裂[8-10]，使落壓比調節器的可靠性恢復至原有設計水平，但其固有可靠性并沒有提高。而提高其固有可靠性，需提高反饋拉簧的結構強度安全裕度。傳統的安全系數設計方法通常是選用更優質材料或加大零件截面尺寸，增加產品體積和質量，但其經濟性隨之下降[11-12]。傳統方法無法將裕度與可靠性指標聯系起來，無法量化衡量[13]。

本文通過可靠性分析，針對反饋拉簧這一反映落壓比調節器可靠性指標的薄弱環節，提出了特征量裕度概率設計方法，在不改變零件截面尺寸的前提下，對反饋拉簧可靠性特征參數進行優化改進設計。

1 落壓比調節器可靠性分析

落壓比調節器的功用是在發動機加力狀態下，通過調節尾噴管臨界截面面積使渦輪落壓比πT按控制計劃實現閉環調節。某落壓比調節器中反饋拉簧疲勞斷裂情況如圖1 所示。疲勞裂紋起源于鉤環彎角的損傷表面，如圖2 所示。落壓比調節器的結構如圖3 所示，對中心元件反饋杠桿進行受力分析如圖4 所示。

圖1 拉簧斷口原始橫向線狀痕跡

圖2 拉簧鉤環彎角的損傷表面

根據受力分析得到反饋杠桿初始力矩平衡方程[14]

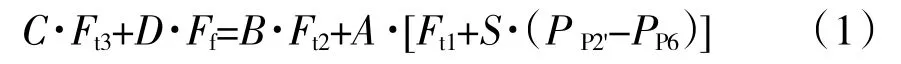
式中：Ft1為P'2腔內彈簧力；Ft2為反饋彈簧力；Ft3為緊固拉簧力；Ff為噴嘴- 擋板閥負載；S 為薄膜有效面積差。

圖3 渦輪落壓比調節器結構

由力矩平衡方程和結構原理可知，反饋拉簧在落壓比調節器中起著重要作用：（1）保證反饋杠桿處于平衡狀態；（2）引入閉環負反饋，使噴口控制閥的移動先快后慢，確保調整過程平穩[15]。若拉簧斷裂，落壓比調節器控制機構平衡被破壞，使發動機噴口發生反復開大或縮小故障。受落壓比調節器空間結構限制，反饋拉簧的絲徑和中徑尺寸較小，在工作狀態下承受疲勞載荷，容易產生疲勞裂紋。經故障模式與影響分析（Failure Mode and Effects Analysis，FMEA），反饋拉簧是落壓比調節器中的設計薄弱環節，其可靠性的高低直接決定落壓比調節器的可靠性。

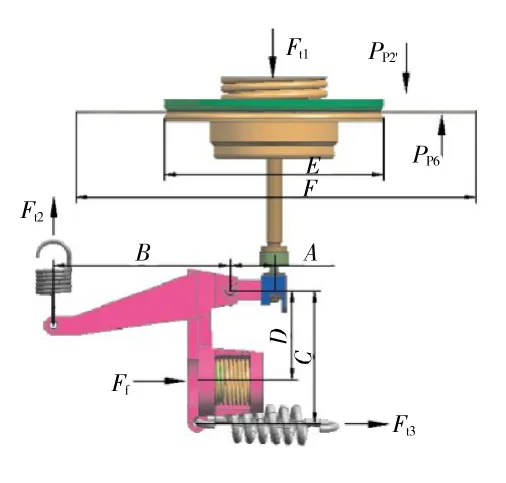
圖4 落壓比調節器反饋杠桿受力分析

2 特征量裕度概率設計

2.1 拉簧傳統安全系數計算

反饋拉簧為長臂圓鉤環結構，其原設計參數為：絲徑d=1.1 mm；中徑D2=8.9 mm；鉤環彎角半徑R=2±0.5 mm；有效圈數為7.75；軸向載荷F=15.48 N。反饋拉簧材料為50CrVA，熱處理后抗拉強度σb≥1470 MPa。在拉伸載荷下，拉簧鉤環的折彎處通常會形成復合的切應力和拉伸應力，再加上應力集中現象，在折彎處易先損傷。因此，在長臂圓鉤環結構拉簧的鉤環彎角內側將產生最大切應力τk[16]

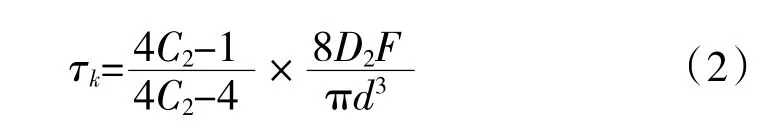
其中：C2=2r2/d；r2=R+d/2。

拉簧許用切應力一般取0.35×σb=514.5 MPa。拉簧鉤環部位最大切應力τk值見表1。從表中可見，當鉤環彎角半徑R 變小時，鉤環最大切應力τk增加，安全系數減小。當R=1.5 mm 為公差下限時，τk=336.2 MPa，安全系數λ＝1.53。由此可知，反饋拉簧有一定的強度裕度，但裕度偏小。

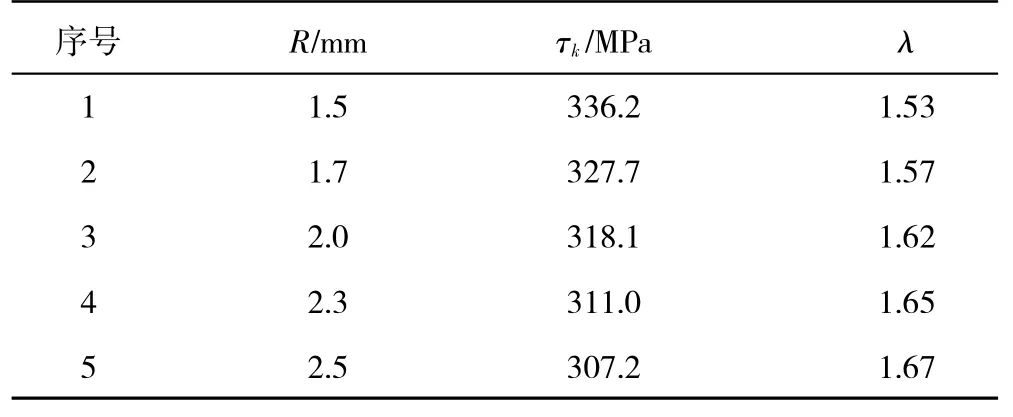
表1 拉簧鉤環部位最大切應力數據

2.2 拉簧可靠性特征量裕度概率設計

為進一步提高落壓比調節器的可靠性，本文提出1 種針對反饋拉簧的特征量裕度概率設計方法。該方法是1 種理論與試驗相結合的工程設計方法，既適用于機械零件的強度裕度，又適用于在零件上不萌生疲勞裂紋的裕度和抵抗熱變形的裕度等，在航天器的機構傳動裕度、密封件密封裕度、防熱結構防熱裕度設計等方面已有應用[13]。優點是將特征量設計值與可靠性指標進行量化計算，使可靠性評估更加精確，最終得到預期的優化設計值；缺點是需要進行大量試驗，獲取必要的樣本量來確定裕度系數，不僅增加研發成本、延長研發周期，也影響其推廣應用。為此，該方法多適用于對可靠性指標要求嚴格且研發周期得到充分保證的場合。特征量裕度概率設計方法的流程如圖5 所示。

圖5 特征量裕度概率設計方法流程

反饋拉簧的特征量裕度概率設計的主要步驟如下：

（1）依據落壓比調節器可靠性分析結果，確定其設計薄弱環節為反饋拉簧。

（2）確定反饋拉簧需優化改進特征參數，建立反饋拉簧結構模型，對鉤環彎角半徑處進行網格加密，如圖6 所示，拉簧應力分布趨勢如圖7 所示。從圖中可見，拉簧所受最大應力處位于鉤環彎角部位。

圖6 拉簧網格劃分

圖7 R=2.0 mm 時拉簧應力分布

對不同的鉤環彎角半徑（R=1.5、2.0、2.5、2.7、3.0 mm），分別建立3 維模型并仿真，如圖8 所示，仿真結果見表2。從表中可見，將反饋拉簧可靠性特征量確定為R，當R 增大時，鉤環彎角處的綜合應力減小。

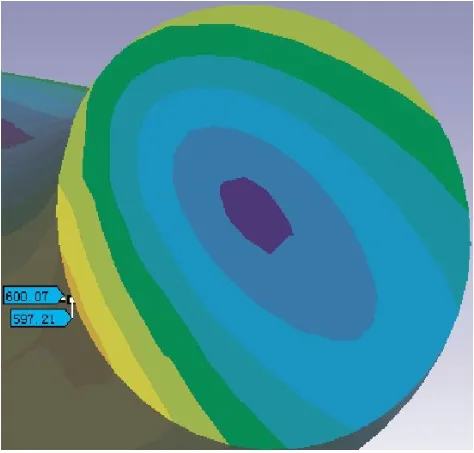
圖8 鉤環彎角截面處應力分布（R=2.0 mm）

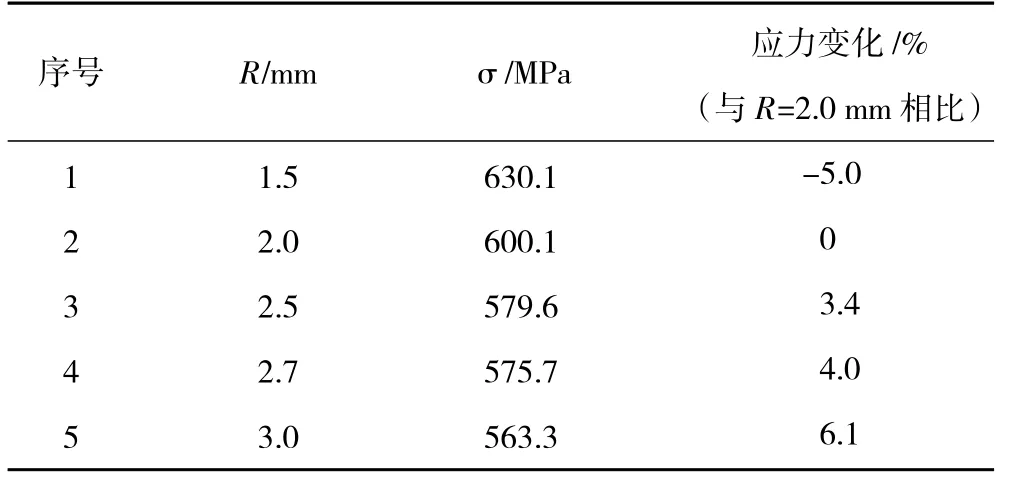
表2 拉簧仿真結果對比

（3）通過理論計算并統計9 件故障拉簧R 數據，R 值均約為1.65 mm，故確定特征參數理論臨界失效值為1.65 mm。

（4）對特征參數臨界值分布規律觀測。選取具有原始橫向線狀痕跡的同批次拉簧，在特征參數理論臨界失效值約為1.65 mm 時確定1 個1.3～2.0 mm 范圍，并將其分為8 組：1.3、1.4、1.5、1.6、1.7、1.8、1.9、2.0 mm。每組選取4 件在高頻彈簧疲勞試驗機上分別進行107次循環疲勞試驗，觀測原始線狀痕跡是否有擴展跡象。當R=1.3、1.4 mm 時，所有拉簧上原始線狀痕跡均有擴展為裂紋的跡象；而當R=1.9、2.0 mm 時，卻均無進一步擴展的跡象。故上述4 組數據均不是特征參數的臨界值，予以剔除。有效觀測樣本量n=4，分別為1.5、1.6、1.7、1.8 mm。

（5）用圖估法進行分布規律檢驗[17]，將每個樣本Xi和累積失效概率Fi在正態概率圖上描點，各點基本分布在1 條直線上（如圖9 所示），則Xi經檢驗不拒絕正態性假設。求得有效樣本均值=1.65 mm，樣本標準差S=0.1291。

圖9 正態概率描點分布

（6）根據分布規律，裕度方程為

式中：X0為特征量的優化設計值；K 為裕度系數；為有效樣本均值。

（7）依據GB 4885 規定，當n=4，置信度γ=0.8時，得到不同可靠性指標下的K，從而求得X0（即優化后的R），見表3。從表中可見，當可靠性指標為0.9999 時，X0=2.49 mm；當可靠性指標為0.99 時，X0=2.18 mm。根據計算結果，將R 設計理論值定為2.5 mm，將R 下限定為2.2 mm，正好是拉簧絲徑Φ（1.1 mm）的2 倍。

表3 不同置信度時的裕度系數及特征量優化設計值

但是R 并非越大越好，R 越大，則鉤環彎角圓弧與鉤環之間的直線段長度L 越短，鉤環相對拉簧軸線的對稱度越難以保證，如圖10 所示，并見表4。從表中可見，當R=3.0 mm 時，L僅為0.89 mm，這將加大拉簧的加工難度。綜合表3、4的計算結果，故將R 上限定為2.7 mm。

圖10 拉簧彎角圓弧與鉤環直接直線段

綜上所述，將鉤環彎角半徑R 由原設計值（2.0±0.5）mm 優化為mm 時，反饋拉簧可靠性提高至0.9999（γ=0.8）。

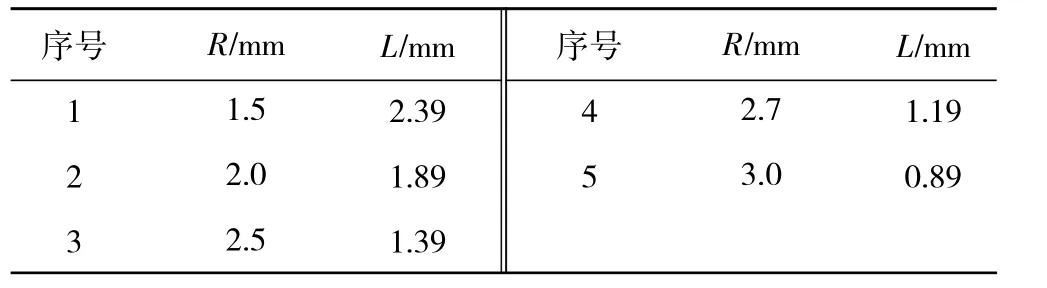
表4 鉤環彎角圓弧與鉤環之間直線段長度參數

3 試驗驗證

選取8件優化改進的反饋拉簧，進行2 輪107次循環疲勞試驗（首輪頻率為16 Hz、次輪頻率為5 Hz），經試驗后理化檢查，8 件試驗件表面均無疲勞裂紋萌生等異常現象。優化改進的反饋拉簧裝入落壓比調節器中進行航空發動機整機壽命試車考核，在試車過程中落壓比調節器工作正常，試驗后經理化檢查，所有參數均合格，反饋拉簧表面無疲勞裂紋萌生等異常現象。

4 結論

本文針對落壓比調節器提出特征量裕度概率設計方法，突破了傳統安全系數設計法的局限性，在不改變零件截面尺寸的前提下，對落壓比調節器中的薄弱環節反饋拉簧進行了優化設計，得到如下主要結論：

（1）采用特征量裕度概率設計方法，將反饋拉簧鉤環彎角半徑原設計值由（2.0±0.5）mm 改為，其可靠性提高至0.9999（γ=0.8）。

（2）改進后反饋拉簧通過2 輪107次循環強化疲勞試驗，理化檢查后未發現疲勞裂紋萌生現象。

（3）在優化設計中發現，當鉤環彎角半徑的下限為拉簧絲徑2 倍時，可靠性裕度能夠滿足設計要求，此規律也可應用于其他類型拉簧的設計。

（4）優化改進的反饋拉簧裝入落壓比調節器中通過了發動機整機壽命試車考核，表明本文提出的特征量裕度概率設計方法解決了落壓比調節器可靠性裕度偏小的問題，優化設計方法有效，具有推廣意義。