凡欲明一法，必設一題

何月豐

“夫學算者，題從法取，法將題驗，凡欲明一法，必設一題。”這句話出自我國南宋時期杰出的數學家楊輝之筆。我第一次讀到是在單墫教授所著的《解題研究》一書中，當時甚為驚訝。只是那本書中僅引用這句話，以此佐證題在數學教學中的重要性，對于這句話的具體釋義則并未給出。

我帶著一點認識，又夾雜著“不甚理解”的遺憾，請教了我縣教科所、中學語文特級教師朱益群老師，朱老師給出了如下釋義：“學算術，題目依據規律（方法）而命制，規律（方法）又對題目做出驗證，凡是想要理解一種規律（方法），必定對應地創設一個題目。”

讀罷，心里既興奮又踏實。興奮的是這句話所表達的意思如我所愿，踏實的是我的想法得到了更好印證。

這讓我聯想到了我所從事的小學數學教學工作。為了讓學生理解小數乘法的算理和算法，為了讓學生理解圖形的周長、面積計算公式，為了讓學生理解公因數、最大公因數的概念，我們都要創設一道道相關的題目。猛然間發現，在數學教學中，例題不正是“必設一題”的最好證明嗎？楊輝的觀點我們一直沿用至今，足見其價值。

至此，讓我又想起了《這才是好讀的數學史》中的一段話：

4000年前的埃及數學已經是相當發達的知識體系，其內容與我們今天所學習的計算和幾何的內容非常相似，我們今天的中小學都還在應用。它被記錄下來，并通過問題的方式進行教學，這些問題的例子都是可以模仿的。

“通過問題的方式進行教學”不正是“凡欲明一法，必設一題”的體現嗎？這無疑進一步證實了題是教學數學的最佳載體，“凡欲明一法，必設一題”是數學教學的最佳方式，且這種方式已經延續了幾千年。所以可以得出這樣一個結論“凡欲明一法，必設一題”貫穿于整個數學教學的歷史中。

現在，我們必須思考另一個問題：題由誰設？

就現在的小學數學教學而言，讓學生獲得知識的題基本已經由教材編寫者設計好了。教材上的題從功能上講，可以分為例題和習題這樣兩大類。例題一般使學生發現和理解知識，習題一般使學生對知識的理解與掌握更加深刻和深化。

可以這樣說，現在小學數學教材上的題已經比較完備了，主要體現在兩個方面：第一是例題的知識體系已經很完備，基本將學生生活和進一步學習數學所必需的基礎知識涉及到了；第二是例題后的習題跟進比較完備，作為必要的補充和深化，體現出了逐步提升的層次結構，能幫助學生更好地理解數學。

那么，這是不是說我們現在的小學數學教學，只要按照教材上編排好的這些題，依次按部就班教學即可？從教學實際來看，不是這么簡單。也就是說，即使教材編寫者設計的題已經比較完備，但教師依舊要根據教學實際需要設計題目。這種設計，主要體現在對習題的改編和創編上。

習題改編，相信很多教師不會感到陌生，因為這在小學數學教學中是一種比較常見的行為，此處不再贅述。

下面，重點談一下習題創編。從“凡欲明一法，必設一題”可知，每一道數學題的創設，都是有明確目的的，這一點，教材上的每一道題都可證明。所以，教師要創編一道習題，自然也要有明確的目的，這不僅體現了教師對教材的深度理解，還常常體現著教師對數學知識本質的深度把握。下面這個例子可以較好地說明此觀點。

【習題創編說明】

平行與垂直是平面內兩直線的位置關系。雖然是在一個課時中教學的，但一般是作為兩個獨立的內容對待的，即平行和垂直各自作為一個教學環節。概念建立后的習題教學，也往往以靜態呈現的方式獨立看待平行和垂直。這樣的習題，對于學生更好地理解和掌握平行與垂直的概念固然有很好的促進作用，是需要的。但是，這樣的習題對于理解平行與垂直之間的關系——尤其是兩者之間的運動變化關系，始終沒有顧及。基于這樣的認識，我萌生了要創編一道體現兩者關系的習題，意圖引導學生從運動變化的視角來看待平行與垂直，更好地理解平行與垂直是平面上兩條直線在運動變化過程中某一時刻的定格，是兩條直線之間的某一特殊位置關系的表征。

【習題教學描述】

教學時，幾何畫板上直接出示下圖頁面。學生觀察頁面上的兩條直線，判斷這兩條線之間的位置關系——相交。

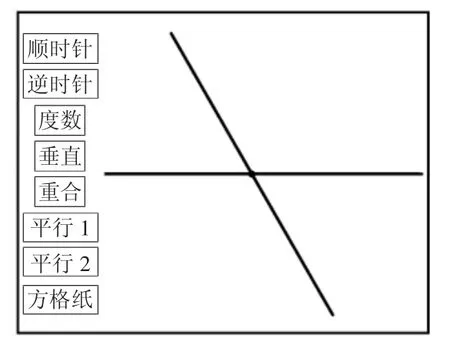
在確認是相交之后，教師提出第一個任務：“如果現在想讓這兩條直線互相垂直，你有辦法嗎？”此時學生都能想到：只要把有點“斜”的那一條直線再稍微旋轉一下即可（說明：課件邊上的按鈕是用英文字母代替的，以防給學生暗示）。按照學生的方式，教師將有點“斜”的那條直線順時針旋轉，并請學生觀察，提醒教師停止的時間。這個時間點是很難控制的，所以課件上還準備了逆時針的按鈕。經過多次調整，在大家都認為是垂直的時候，出示度數驗證，如果還不垂直，可通過“垂直”按鈕準確實現垂直。（如下圖）

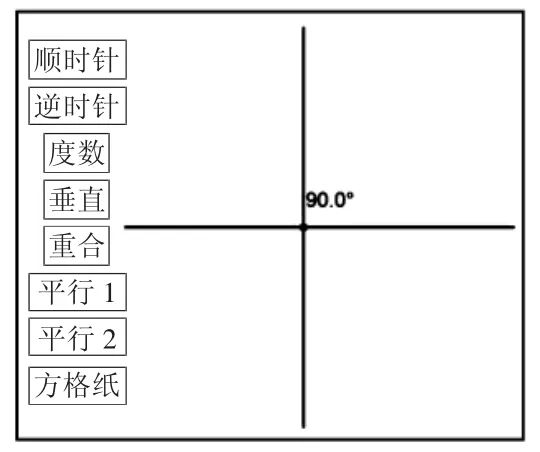
在上述過程中，來回多次調整看似多余，其實是關鍵，因為正是這個過程，讓學生深刻體會到了垂直是兩條直線在運動變化中某一特殊時刻的瞬間定格。

完成上述教學之后，教師提出第二個任務：“如果這條直線繼續順時針旋轉，會發生什么情況？”這里不著急請學生回答，讓學生先想象一下。學生根據想象，會發現繼續順時針旋轉，兩條直線就會重合。根據學生的想法，教師課件演示，繼續順時針旋轉，直到重合。

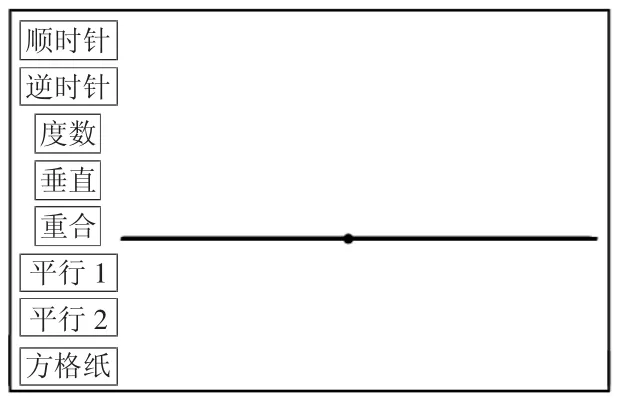
上述教學實現了從相交到重合的運動變化。同樣，學生在這個運動變化的過程中就體會到，重合也無非是兩條直線在運動變化過程中的一個瞬間定格而已。

完成上述教學之后，教師提出第三個任務：“如果現在想使這兩條直線平行，你有辦法嗎？”學生自然會想到：只要把其中一條直線向下或者向上平移即可。運用學生的方法，課件演示向下平移。為了更好地展現“平行”，可借助方格紙進一步幫助證明。一次平移之后，繼續思考：還能不能繼續移動？這就是“平行2”按鈕的作用了。

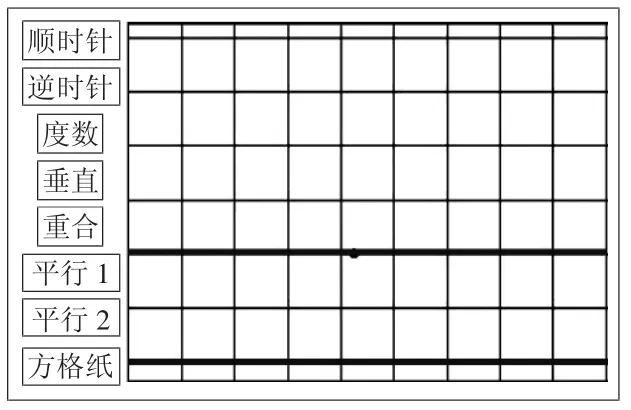
從這道習題的設計和教學可以看出，此題一方面在進一步鞏固學生對于平行與垂直的理解，另一方面——也是本題創編的核心目標——引導學生從運動變化的視角看待垂直、重合與平行的關系，加深對平行與垂直的理解。

所以，題由誰設？就我們現在的小學數學教學而言，題主要是由教材編寫者設計。但這不是全部，題，也需要作為教學執行者的教師自己來設計。

教材編寫者設計的題，是基于數學知識體系的邏輯結構和教學的一般原理考慮的，具有很強的普適性。教師自己設計的題，是基于自己教學的具體實際需要和對數學的自我理解而考慮的，具有很強的個人色彩。當然，兩者的目的一定是一致的，都是為了學生能更好地學習數學。

綜上所述，作為一線數學教師，不僅要努力做好“習題執行者”這個基礎角色，也要努力成為“習題設計者”這個“高光”角色。特別值得一提的是，教師創編習題的過程，也能有效促進自我的專業成長。

“凡欲明一法，必設一題”，于學生，于教師，同樣重要。