多重介質油藏數值模擬異構并行算法研究

陳元科，張冬梅，崔書岳，張宇洋

(1.中國地質大學(武漢)計算機學院，湖北 武漢 430074；2.中國石化石油勘探開發研究院，北京100081)

1 引言

塔河油田是古巖溶與多期構造運動共同作用下生成的縫洞型碳酸鹽巖油藏，儲集體類型多樣，具有非均質性較強等特點[1]。油藏數值模擬是定量評價地層流體流動規律的主要方法[2]，縫洞型油藏的儲滲空間主要由溶蝕孔洞和裂縫組成，單元間連通性較差、油氣水三相關系復雜[3 - 7]。針對該類復雜油藏，嚴俠等[8]提出基于離散縫洞網絡模型和模擬有限差分法的刻畫方法；張冬麗等[9]提出刻畫不同尺度裂縫的數值模擬方法；康志江等[10]針對復雜油藏介質建立滲流耦合模型，形成多重介質數模的體系基礎；邸元等[11]基于有限體積法采用非結構化網格建立多孔介質多相流數值模擬方法。KarstSim是中國石油化工股份有限公司研發的軟件，能針對縫洞型碳酸鹽巖油藏進行有效的數值模擬[11]，本文基于KarstSim開展并行多重介質油藏數值模擬算法研究。

縫洞型油藏復雜的多孔介質和油氣水三相關系使數值模擬計算量巨大，為提高模擬效率必須開展并行計算研究[12]。目前主流的并行技術有3種：基于中央處理器CPU(Central Processing Unit)的分布式并行、基于圖形處理器GPU(Graphic Processing Unit)的統一計算設備架構CUDA(Compute Unified Device Architecture)并行和基于CPU-GPU的異構并行。異構并行結合CUDA和分布式并行的技術特點，利用CPU實現粗粒度進程并行同時采用GPU實現細粒度線程并行。并行油藏數值模擬研究多集中在雅各比矩陣組裝和線性方程組求解，雅各比矩陣組裝分別計算各網格的流動項，線性方程求解多采用Krylov子空間求解方法中的共軛梯度CG(Conjugate Gradient)及改進算法，計算量大。Yang等[13]提出基于混合有限元法、隱式向后歐拉法和Newton-Krylov法的可拓展全隱式求解器，實現兩相流油藏數值模擬在多核集群上的分布式并行；李毅等[14]通過網格分區、多CPU高性能計算庫Aztec和網格分解軟件METIS實現分布式并行縫洞型油藏數值模擬；Werneck等[15]基于分布式并行實現了并行CG法及改進算法并應用于單相流油藏模擬；李政等[16,17]針對油藏模擬中雅各比矩陣的稀疏模式，設計了一種塊混合結構稀疏存儲格式BHYB和線程組并行策略，并提出了基于CPU-GPU異構體系的并行BCPRP(Block Correction Proceduce via Reconstruction)預處理方法，在黑油模型上得到了較好的求解速度。基于分布式并行的油藏數值模擬的研究多通過網格劃分實現并行方程求解，但網格劃分通常會丟失一些流動信息；基于GPU的線性方程組求解應用非常廣泛，結合矩陣預處理方法對矩陣信息的影響較少，比直接進行網格劃分更為準確。

傳統黑油模型難以用于縫洞型油藏數值模擬，本文針對多重介質模型數值模擬計算耗時的問題，提出一種基于CPU-GPU異構并行架構的數值模擬算法。基于GPU實現并行雅各比矩陣組裝和線性方程組求解法，進一步研究多CPU下具有可擴展性的分布式并行數值模擬算法，提高縫洞型油藏數值模擬效率。

2 多重介質模型

多重介質縫洞型油藏中的介質主要由孔隙、裂縫和溶洞組成，裂縫是流動的主要通道，基質的孔隙度和滲透率較低，流體有油、氣、水三相，其中氣體也能溶解于油相，各相流體流動服從達西定律。等效模型劃分為基質和介質，流動發生在基質之間的介質上，等效模型如圖1所示[18]。

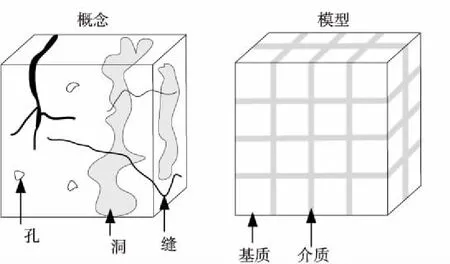
Figure 1 Equivalent model圖1 等效模型

孔隙中油、氣、水各組分的連續性方程如式(1)[10]所示：

(1)

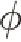
裂縫、溶洞中油、氣、水各組分的連續性方程如式(2)[10]所示：

(2)

孔隙、裂縫與溶洞中油、氣、水各組分的運動方程如式(3)[10]所示：

(3)

其中,K表示絕對滲透率；Krβ代表各相具有的相對滲透率；μβ表示各相的黏度；pβ表示各相的壓力；g表示重力加速度；D表示介質所在深度。

由連續性方程和運動方程可得孔隙、裂縫和溶洞中油、氣、水各組分的質量平衡方程如式(4)所示：

(4)

其中,γog=(ρo+ρdg)g,γo=ρog,γw=ρwg。

各相飽和度和毛細管壓力輔助方程如式(5)[11]所示：

(5)

其中,pcow、pcog分別表示油水、氣油間的毛細管壓力。

將介質劃分為不同區塊，各區塊再劃分為溶洞、裂縫、基質3個單元。各單元之間、相連區塊之間各單元的流體流動有連續性方程：

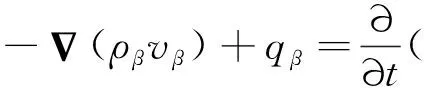
(6)

其中qβ是β相的源匯項。

用有限體積法對式(6)進行空間離散得到非線性方程[11]：

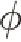
(7)

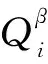
在滿足達西定律的流動中，流動項可表示為式(8)[11]所示：

(8)

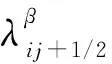
(9)

γi,j定義為單元i和單元j之間的連通度：

(10)

Ψ是單元中流體的流動勢：

(11)

式(10)中,Aij表示單元i和單元j交界面的面積；di,dj分別表示單元i和單元j的中心點到2個單元交界面的距離；Kij+1/2表示單元i和單元j的平均滲透率；式(11)中，Li表示單元i的中心點到高度參考面的距離。

3 異構并行多重介質油藏數值模擬算法

多重介質模型的迭代過程包括雅各比矩陣組裝和線性方程組求解2個主要耗時步驟。本文基于消息傳遞接口MPI(Message Passing Interface)在多個GPU上實現雅各比矩陣組裝，各分布式結點分別調用GPU計算分配任務；方程求解部分通過CUDA并行求解庫實現，該庫包含多種在GPU上實現的并行矩陣預處理方法和并行基礎線性方程求解方法，如不完全LU分解法(incomplete Lower-Upper factorization)和穩定雙共軛梯度法BiCGStab(BiConjugate Gradient Stabilized method)。

3.1 基于CPU-GPU異構的多重介質油藏數值模擬算法

本文對雅可比矩陣組裝和線性方程組求解展開并行工作，進而降低數值模擬總耗時，基于分布式并行雅可比矩陣組裝算法和GPU并行BiCGStab法的線性方程組求解方法實現異構并行多重介質油藏數值模擬算法。通過MPI為各CPU分配計算任務，各CPU通過GPU實現雅可比矩陣組裝。GPU并行時將數據從主機內存傳輸到設備內存，針對數據交換延遲，利用GPU的異步發送功能將數據劃分為多個數據段，發送的同時執行計算任務，以減少時間開銷。調用GPU完成計算后各CPU通過MPI通信函數傳輸結果。CUDA線性方程求解庫不支持多GPU并行且存在數據依賴關系，故將各自組裝的矩陣數據規約傳輸到主CPU，由主CPU執行GPU并行求解算法。根據收斂情況，將解向量廣播到其他各CPU用于更新流動項。多重介質油藏數值模擬異構并行算法流程如圖2所示。

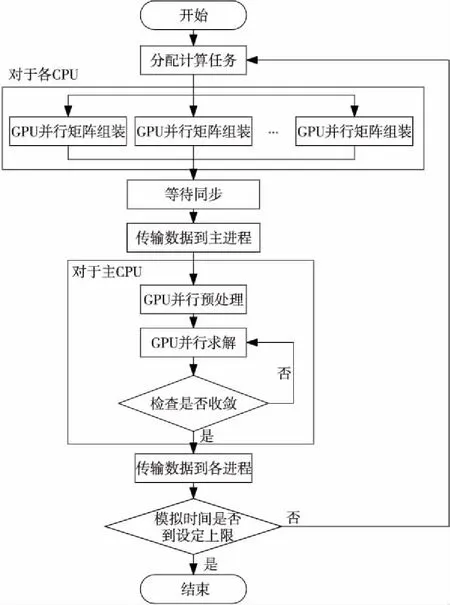
Figure 2 Flow chart of heterogeneous parallel algorithm of multi-media oil numerical simulation圖2 多重介質油藏數值模擬異構并行算法流程圖

3.2 基于GPU并行的矩陣組裝和方程求解

縫洞型油藏非均質性強，多重介質模型建立的線性方程組系數矩陣非常稀疏，為提高求解效率，使用塊壓縮稀疏行BSR(Block Compressed Sparse Row)格式對稀疏矩陣進行壓縮。各行組的非零元素表示為：

ABlock=Ai,j

(12)

其中,ABlock表示i行j列非零位置的3×3子矩陣。

本文基于CUDA實現GPU并行雅可比矩陣組裝和GPU并行預處理BiCGStab法。在組裝雅可比矩陣的過程中，要計算各網格通過介質與相連網格產生的流動信息，單元中共有n個網格對應矩陣中的n個行組。矩陣中的行組被劃分為油氣水三相，子矩陣結構如圖3所示。對矩陣行組的各非零子矩陣調用3×3個GPU線程實現并行計算。

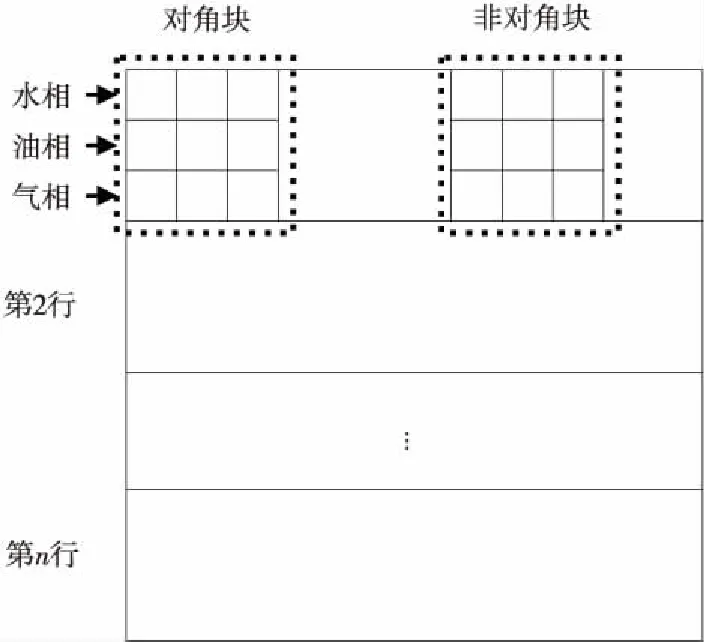
Figure 3 Jacobi matrix structure圖3 雅可比矩陣結構

預處理BiCGStab法通過調整矩陣結構提高迭代求解的收斂性能。本文通過cuSparse庫對矩陣進行不完全ILU分解，得到預處理后的上三角矩陣和下三角矩陣，再對線性方程組的解空間進行搜索，其中矩陣向量乘是主要的計算步驟。GPU實現并行矩陣向量乘的過程如圖4所示，GPU分配矩陣向量乘任務對應的數據，各線程調用一個計算單元執行一次乘操作，具體通過CUDA庫函數實現迭代求解，收斂得到當前時刻三相流動項的變化值。

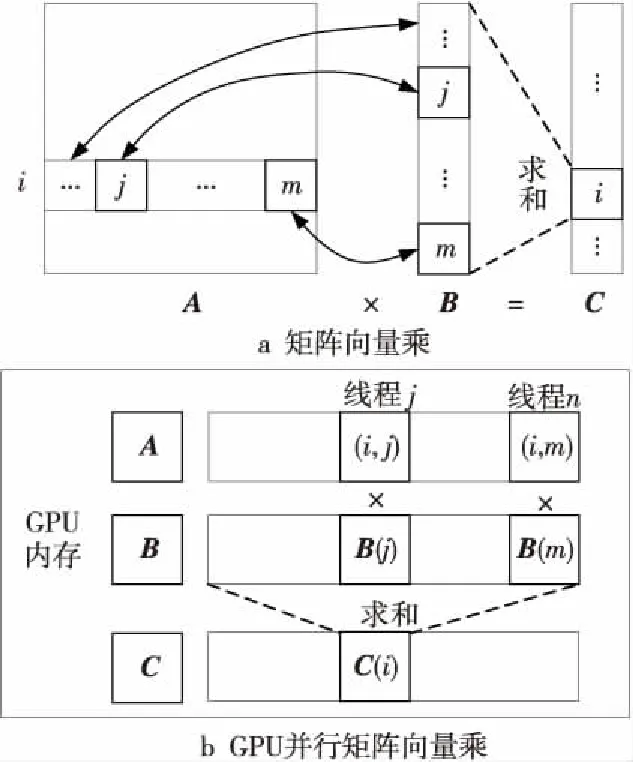
Figure 4 Parallel matrix vector multiplication圖4 并行矩陣向量乘

3.3 基于CPU并行的雅可比矩陣組裝

為進一步提高矩陣組裝并行效率，基于異構并行架構實現多CPU調用多GPU。統計所有非零位置子矩陣的數量M，為N個CPU核心分配相近數量的子矩陣計算任務，再由N個CPU核心分別調用對應GPU實現負載均衡，如圖5所示。

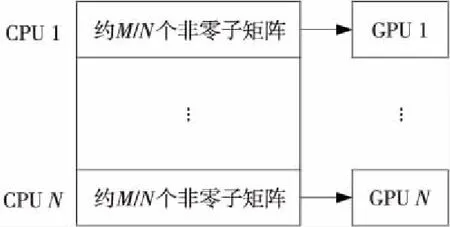
Figure 5 Calculation task partition圖5 計算任務分配

計算任務所需數據從異構框架中的主機端發送到設備端，從設備端開始GPU并行。按求解執行順序將數據劃分為多個部分，先發送第1部分，后續發送的同時執行求解任務，以減少時間開銷。調用MPI數據交換函數時進程需等待，調用次數越多總等待時間越長。本文將通信數據統一存放到臨時數組，只需調用一次數據交換函數，降低了時間開銷。各結點完成計算任務后，通過MPI異步數據傳輸函數MPI_REDUCE將各CPU計算的矩陣數據傳輸回主CPU；用REDUCE函數同步數據以減少各CPU在數據傳輸后的緩沖區讀取次數和時間開銷；數據同步到主CPU后，再由主CPU開啟CUDA核函數進行GPU線性方程組求解。

4 數值實驗

實驗將本文提出的并行算法和串行油藏數值模擬軟件的運行結果進行比較。對塔河油田3個不同規模的問題進行模擬計算，驗證并行算法在模擬結果上的準確性和可擴展性。并行平臺由12個主頻為3.4 GHz的4核心CPU(Intel core i5-7500)和12塊NVIDIA GeForceGTX1060組成，搭載Linux操作系統，各結點安裝MPICH2和CUDA9.1。

4.1 并行模擬結果對比

塔河油田S04單元模型網格如圖6所示，該模型網格數是399 158，連接數1 064 405，稀疏矩陣非零元素數量2 527 968。除裂縫和溶洞介質外，油藏基質部分滲透率低，各單元有不同孔隙度和絕對滲透率，相對滲透率和毛細管壓力曲線相同。S04單元的基本參數如表1所示。

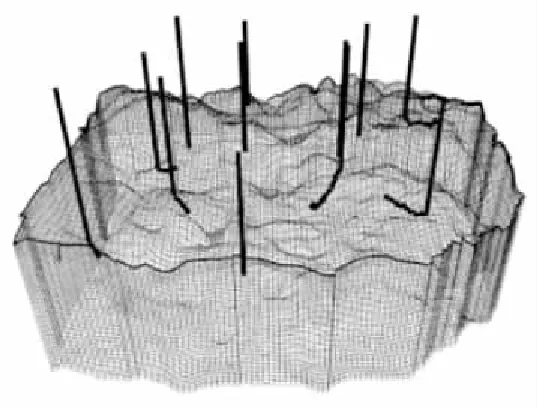
Figure 6 Grid of unit S04圖6 S04單元網格

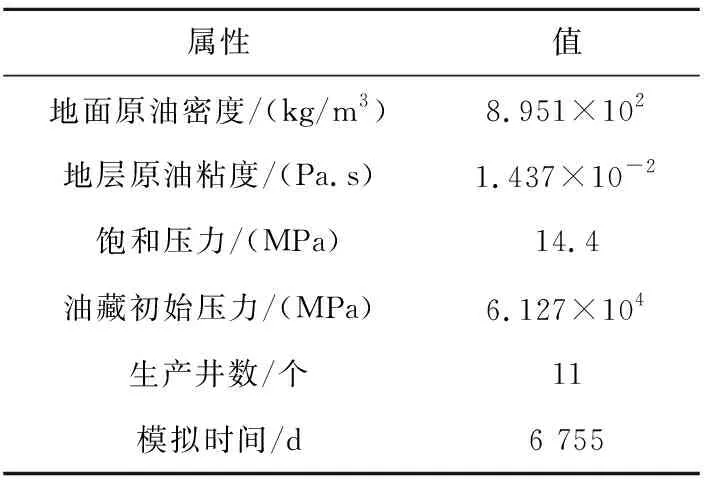
Table 1 Basic parameters of unit S04 表1 S04單元基本參數

本文采用3個的總計12個CPU核心對S04單元開展實驗，對比模擬結果的累積產油量、單元中TK455井的含水率和油藏壓力。圖7所示為累積產油量曲線，圖8所示為TK455井的含水率曲線，圖9所示為油藏壓力曲線。

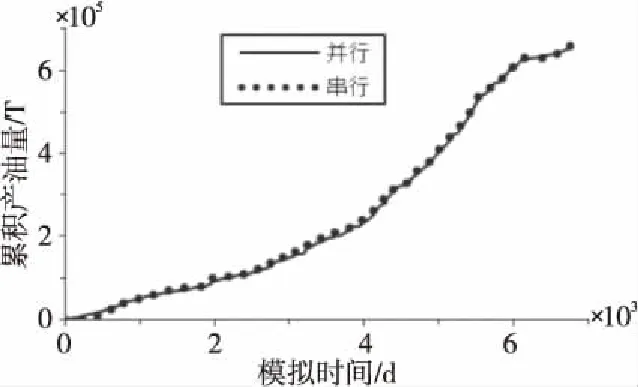
Figure 7 Comparison of simulated remaining oil quality of unit S04圖7 S04單元模擬累積產油量對比

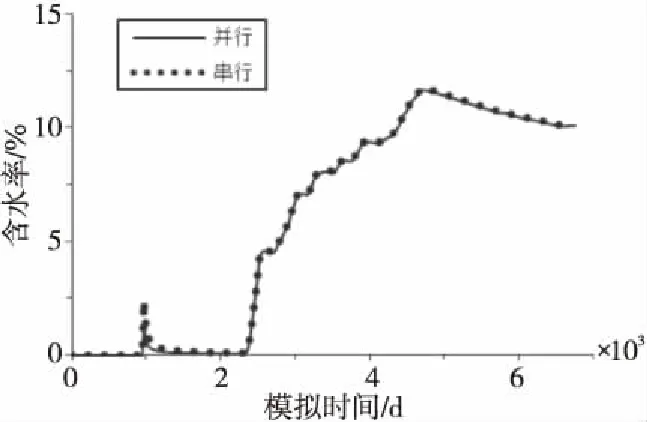
Figure 8 Comparison of the moisture ratio of well TK455圖8 TK455井模擬含水率對比

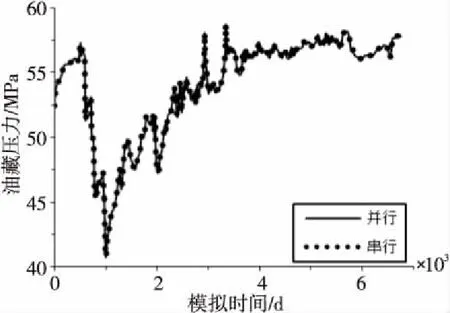
Figure 9 Comparison of bottom pressure data of unit S04圖9 S04單元模擬油藏壓力數據對比

對比并行算法與串行模擬曲線可知，模擬結果幾乎相同，本文提出的并行算法能正確地模擬計算S04單元。

4.2 并行加速效果對比

并行加速效果由加速比進行衡量，包括矩陣組裝加速比、求解加速比和總體加速比。對3個不同規模的單元數據應用異構并行算法開展數值模擬。615B規模相對較小，單元數約為4萬，非零元素數量約22萬，線性方程組系數矩陣的稀疏度較低;S80規模和線性方程組規模都比615B單元更大，單元數約9萬，非零元素數量約48萬；S04單元規模最大，單元數接近40萬，矩陣非零元素數量達到252萬。615B單元與S80單元的基本參數如表2所示，其中稀疏程度定義為：非零元素數量/(單元數)2。

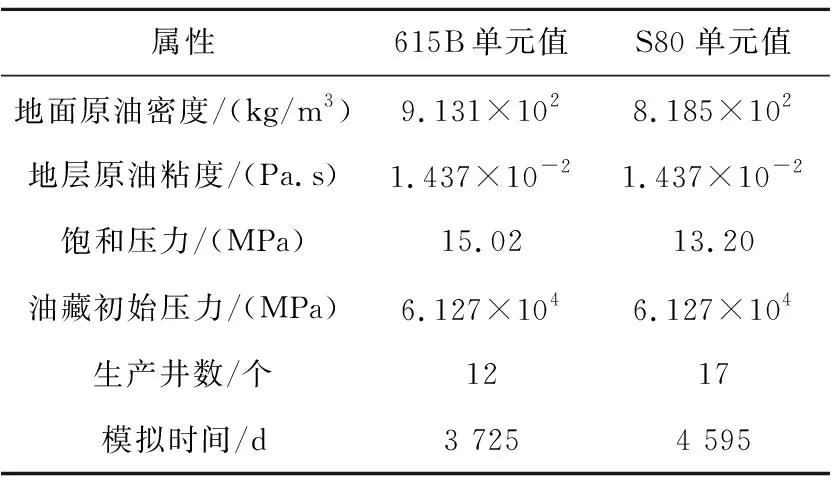
Table 2 Basic parameters of unit 615B and S80 表2 615B單元與S80單元的基本參數

本文調用2～12個CPU核心，各CPU核心分別對應MPI環境中的一個進程，并分別調用一塊GPU。分別對615B、S80和S04單元開展異構并行數值模擬實驗，結果如圖10所示。隨著CPU核心數增加，各單元線性方程組組裝加速比接近線性；當CPU核心數超過8時，算法對615B單元和S04單元仍有較好的可擴展性，但對S80單元的可擴展性明顯減弱。

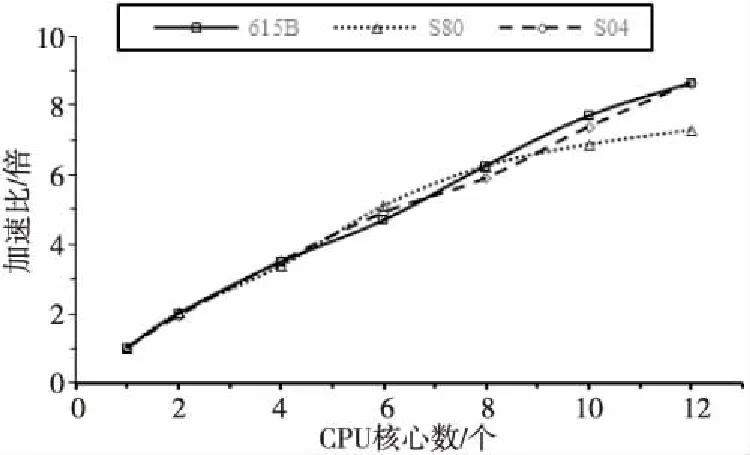
Figure 10 Matrix assembly parallel scalability curve of each unit圖10 各單元矩陣組裝并行可擴展性曲線

對比線性方程組求解部分的預處理耗時、迭代求解耗時、平均各迭代耗時和求解總耗時。串行軟件僅調用一個CPU核心，并行算法調用12個CPU核心和12個GPU。實現超過2倍的預處理加速比和3倍以上的迭代平均加速比，總體加速效果達到預期，結果如表3所示。

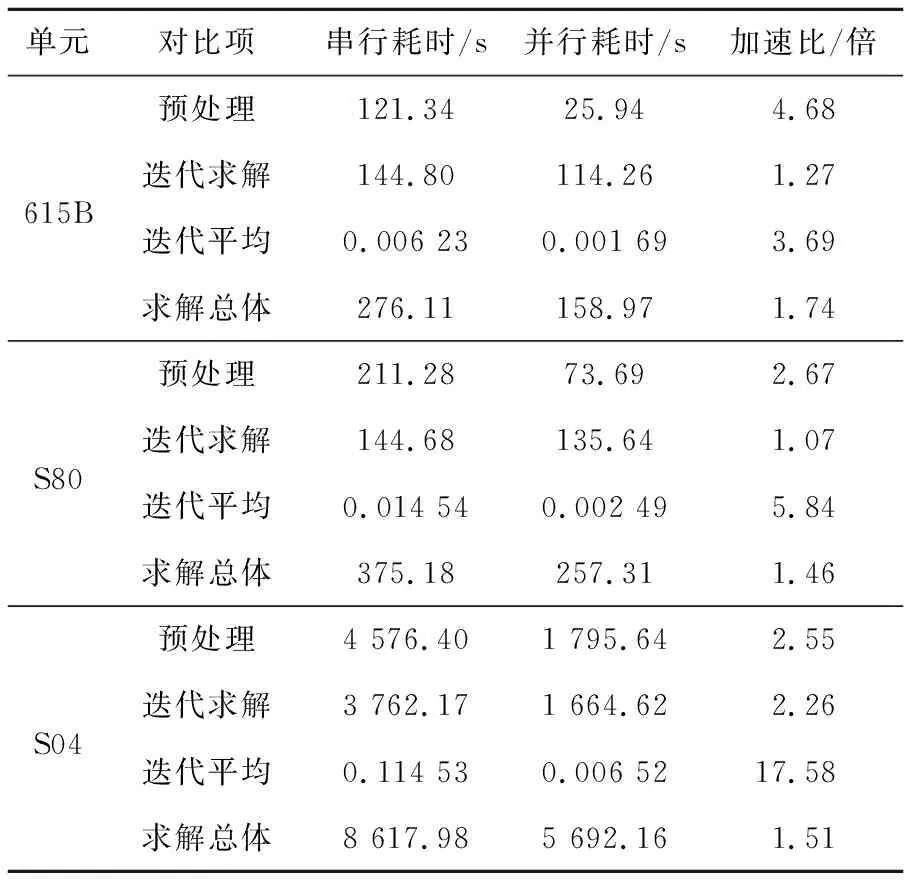
Table 3 Equation system solving speedup of each unit表3 各單元方程組求解加速比

配置12個CPU核心3個單元數值模擬的總體并行加速比如表4所示，各單元數據都實現了2倍以上的總體加速比。

綜上所述，本文設計的異構并行算法能夠充分實現加速效果，模擬結果也與串行油藏數值模擬軟件結果基本一致。

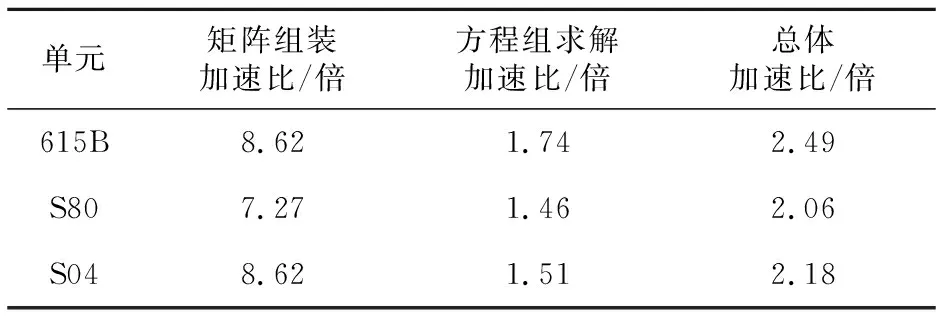
Table 4 Overall parallel speedup of each unit表4 各單元總體并行加速比

5 結束語

本文采用多重介質模型刻畫縫洞型油藏，但數值模擬耗時巨大。為提高多重介質模型計算速度，本文基于異構并行架構，針對多重介質模型耗時最高的線性方程組組裝和求解部分，設計多重介質油藏數值模擬異構并行算法。

本文針對塔河油田縫洞型油藏3個不同規模的單元615B、S80、S04進行并行數值模擬實驗，615B和S04單元的實驗結果表明，多重介質油藏數值模擬異構并行算法具有較好的準確性，能有效提高縫洞型油藏數值計算速度。S80單元的模擬結果表明，并行矩陣組裝的可擴展性有優化的空間。未來將對超大規模網格的油藏數據開展實驗，優化多重介質油藏數值模擬異構并行算法，提高計算效率。