融合信息技術教學 發展學生推理能力

汪元興

[摘? 要] 信息技術與學科融合已成趨勢，教學設計應根據實際，融合現代信息技術整合教學內容，改進教學方法，提高實效. 文章以“三角形”的章起始課“認識三角形（第1課時）”的教學設計為例，闡述了如何融合信息技術，發展學生推理能力的一些做法與思考.

[關鍵詞] 信息技術;融合;概念教學;推理能力

《義務教育數學課程標準（2011年版）》（以下簡稱《課標》）提出：“信息技術的發展對數學教育的價值、目標、內容以及教學方式產生了很大的影響.數學課程的設計與實施應根據實際情況合理地運用現代信息技術，要注意信息技術與課程內容的整合，注重實效.”《國家中長期教育改革和發展規劃綱要（2010-2020年）》提出要“強化信息技術應用”，教師要更新教學觀念，改進教學方法，提高教學效果.自2016年以來，“數學核心素養”開始備受關注，而“邏輯推理”就是六項關鍵能力之一. 現以北師大版七年級下冊“認識三角形（第1課時）”的教學設計為例，談談如何融合現代信息技術，鼓勵學生運用信息技術自主學習，發展學生邏輯推理能力的一些做法與思考.

基本情況分析

1. 教材分析

內容選自北師大版七年級下冊數學教材第四章“三角形”的第一節“認識三角形（第一課時）”. 小學教材已出現“三角形”，但未正式定義;通過撕紙、測量等方法歸納出“三角形的三個內角和等于180°”.在七年級，本節課是“三角形”的起始課，將為后面學習三角形的三邊關系、三角形的全等以及全等三角形的判定等打下基礎. 因此，本節內容具有承上啟下的作用.

2.學情分析

授課班級為數字平板走讀班，課室配有一體機，學生人手一臺平板，能夠熟練地使用早上數字課堂系統，能夠積極地參與數學學習活動.在小學學過三角形的一些初步知識，能在生活中抽象出三角形的幾何圖形;通過撕紙、測量等方法歸納出“三角形的內角和為180°”，具備了直觀操作的經驗. 在第二章，學生對兩直線平行的條件以及平行線的特征進行了探索，具備了利用平行線的結論推導出“三角形的內角和為180°”這一結論的基礎.

3. 教學目標

（1）通過觀察、抽象，理解三角形的概念，了解直角三角形的概念;

（2）通過探索證明“三角形的內角和等于180°”，發展學生的邏輯推理能力;

（3）會按內角的大小對三角形進行分類.

4. 教學的重點與難點

重點：三角形的概念，探索證明“三角形的內角和等于180°”.

難點：探索證明“三角形的內角和等于180°”.

■ 教學過程

1. 環節一：情境引入

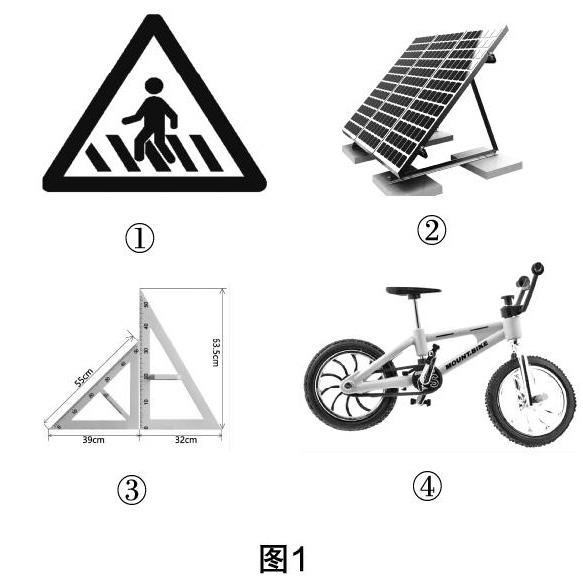
師：觀察圖1中的四幅圖，相同的圖形是什么？

教師活動：PPT展示生活中有關三角形的圖片，引導學生觀察，并另舉實例，引出課題.

學生活動：觀察圖片，感受生活中的三角形.

設計說明? 引導學生從生活實例中抽象出三角形圖形，感受數學知識源于生活，激發學生學習數學的興趣，同時為抽象出數學化的三角形作鋪墊.

2. 環節二：展示目標（學習目標）

（1）理解三角形的概念及其基本要素：邊、角、頂點，會用符號“△”表示三角形;

（2）探索并證明三角形的內角和定理（重點和難點）;

（3）會按角的大小對三角形進行分類，了解直角三角形的概念.

教師活動：通過早上課堂系統，同屏PPT內容，展示學習目標.

學生活動：閱讀學習目標.

設計說明? 同屏展示學習目標，讓學生明確本節課的學習任務.

3. 環節三：教師導學

問題：面對一個新的幾何對象——三角形，我們該怎樣研究它呢？“溫故而知新”，我們可以從已有的學習經驗中找到思路. （回顧上一學期“角”的學習，我們研究了角的哪些內容？是按怎樣的路徑展開研究的？PPT展示）

角的定義→角的表示→角的分類→角的性質（比較大小）.

下面，我們能不能嘗試著按類似的途徑對三角形展開研究呢？

設計說明? 引導學生類比角的學習方法，嘗試對三角形展開研究，進一步體會學習幾何對象的一般套路.

【導學一：三角形的概念及其符號表示】

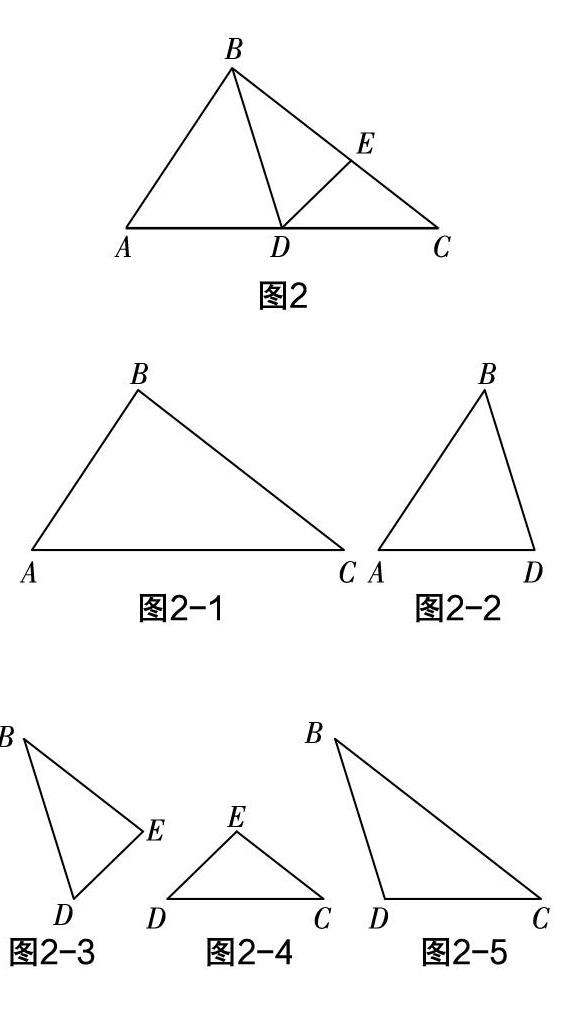
師：你能從圖2中找出幾個不同的三角形？這些三角形有什么共同特點？（說明：PPT先展示圖2，再展示拆分的圖2-1至圖2-5，隨后引導學生閱讀課本P81，回答下列問題）

問題1：什么叫作三角形？其基本要素是：_____________.

問題2：圖2-1的三角形可表示為：_____________.

問題3：圖2-1的三角形的三條邊可表示為：_____________.

（說明：圖2-1為課本P81的圖）

教師活動：通過早上課堂系統推送問題，觀察學生作答情況，展示學生典型作答，引導學生細讀教材，掌握學習幾何概念的一般方法.

學生活動：先獨立在平板上作答，再與同學交流，修正錯誤，規范書寫符號.

設計說明? 先讓學生獨立思考，再引導學生閱讀課本第81頁相關內容，在“問題1”中提示學生劃出關鍵詞句.根據章建躍博士有關概念教學的理論，引導學生結合生活中三角形的圖例，去掉物理屬性，抽象出純粹三角形圖形的一般特征（有三個頂點、三條邊、三個角），進而獲得三角形的概念. 重點突出“不在同一直線上”“首尾順次相接”，為后面理解三角形的三邊關系及其他性質打好基礎.在“問題2”強調用符號表示三角形時要簡明、準確，規定要用“△+大寫字母”;在“問題3”直接說明邊的表示可用兩個大寫字母（如BC），也可以用一個小寫字母（如邊BC也可表示為a）.

【導學二：探索和證明三角形的內角和定理】

（1）小學時你是如何得到三角形三個內角的和是180°的？

（2）閱讀課本第82頁“做一做”，你能理解小明的思路嗎？嘗試把證明過程寫出來.

（3）交流展示. （用希沃授課助手投影學生的推理過程）

（4）歸納結論：三角形三個內角的和等于180°.

教師活動：出示問題，觀察學生課堂實際表現，適時給予引導，包括明確推理的必要性、如何由“180°”想到“引平行線”、如何規范書寫推理過程等.

學生活動：按老師要求獨立思考后小組交流展示.

設計說明? 回顧在小學時探索“三角形的內角和等于180°”的方法，感受歸納推理;同時指出撕紙、測量會有誤差，需要更為嚴謹的邏輯推理.通過提示由“180°”，想到“互補”“平角”等，引發學生思考如何用數學的方法移動角，將三個角集中到三角形的某一個頂點，能否利用平行線的有關性質說明這個結論，進而引導學生想到“引平行線”的方法.這一環節，先讓學生獨立思考，再交流展示.通過希沃授課助手投影學生的推理過程，或者利用早上系統同屏展示不同解答，及時暴露學生可能存在的問題，經師生評議修正，深化理解;學生可以截屏筆記，省時高效.這樣做能夠將直觀感知和邏輯推理結合，由直觀思維過渡到抽象思維，更好地發展學生的邏輯推理能力.

【檢測1】

（1）在△ABC中，∠A=80°，∠B=∠C，則∠C=（？搖？搖? ? ）

A. 80°

B. 50°

C. 60°

D. 不確定

（2）已知△ABC中，∠A ∶ ∠B ∶ ∠C=2 ∶ 3 ∶ 4，求∠A，∠C的度數.

（3）閱讀課本第82頁“議一議”，回答相關問題.

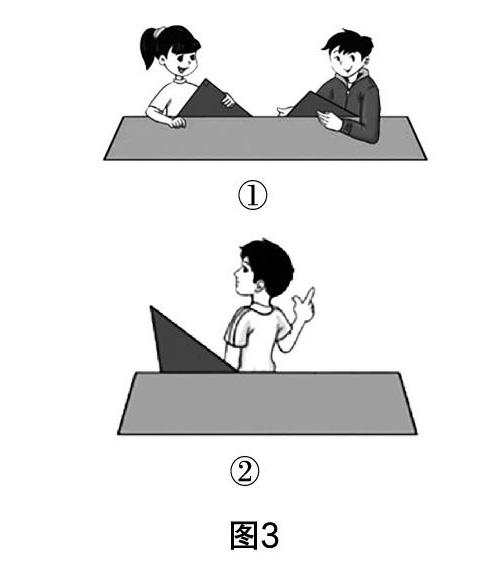
（4）圖3①中小明所拿三角形被遮住的兩個內角是什么角？小穎的呢？

圖3②中三角形被遮住的兩個內角可能是什么角？將結果與圖3①進行比較.

教師活動：推送問題，觀察學生的掌握情況，評講議一議圖3②后，板書“分類討論”.

學生活動：按要求作答，口述解題思路.

設計說明? 鞏固練習，加深理解.在議一議圖3②中滲透分類討論思想.

【導學三：按內角的大小把三角形分類】

教師活動：平板推送，同屏投影，板書“Rt△ABC”，要求學生做筆記（可截屏）.

學生活動：同屏閱讀，按要求做筆記.

設計說明? 先讓學生閱讀課本，再同屏投影，引導學生做筆記，明晰三角形按角的大小分為三類，同時突出直角三角形的符號表示和直角三角形兩銳角互余的結論.

【檢測2】

（1）觀察圖5中的三角形，并把它們的標號填入相應的方框內.

（2）一個三角形兩個內角的度數分別如下，這個三角形是什么三角形？

①30°和 60°;

②40°和 70°;

③50°和 20°.

（3）在直角三角形中，有一銳角是另一個銳角的2倍，求這個銳角的度數.

教師活動：出示問題，觀察學生的作答情況，展示并引導學生評議第3題的作答情況.

學生活動：回答問題，展示第3題的解答過程，全班評議，規范解答格式.

設計說明? 檢測三角形按角分類，及直角三角形兩銳互余這一性質.利用早上課堂系統的同屏對比功能，重點展示學生對第3題的不同解法（預設學生可能會設“這個銳角為x度”，也可能會設“另一個銳角為x度”），優化課堂教學，提升課堂教學效率.

4. 環節四：課堂小結

問題1：這節課學習了什么內容？

問題2：我們是如何探索和說明三角形內角和為180°的？

問題3：對于今天的學習，你還有什么疑問？

問題4：類比角的研究過程，下節課我們將學習三角形的什么內容呢？

教師活動：口頭引導學生回顧本課所學內容，同屏投影主體內容.

學生活動：口頭小結，截屏做筆記.

設計說明? 以反思性問題（如問題2）提升課堂小結的思維層次.先讓學生口述，再同屏投影，讓學生截屏做筆記，突出本節課主體內容.

5. 環節五：課堂檢測 （早上課堂系統在線考試）

（1）已知△ABC中，∠A=70°，∠B=60°，則∠C=（? ? ?？）

A. 50°? ? ?B. 60°? ? ?C. 70°? ? ?D. 80°

（2）若一個三角形三個內角度數的比為1 ∶ 3 ∶ 5，則這個三角形是（? ? ?？）

A. 直角三角形? ? ? B. 銳角三角形

C. 鈍角三角形? ? ?D. 無法確定

（3）直角三角形中，有一個銳角是另一個銳角的4倍，則這個直角三角形中一個銳角的度數是（? ? ? ）

A. 9°? ? ?B. 18°? ? ?C. 27°? ? ?D. 36°

（4）如圖6，在△ABC中，∠C=60°，沿圖中虛線截去∠C，則∠1+∠2等于（? ?）

A. 120°? ? ? ? ?B. 180°

C. 240°? ? ? ? D. 260°

（5）如圖7，在△ABC中，∠ABC，∠ACB的平分線BE，CD相交于點F，∠ABC=30°， ∠A=70°，則∠BFC等于（? ? ?？）

A. 100°? ? ? ? ? ? ? B. 110°

C. 115°? ? ? ? ? ? ? D. 125°

教師活動：早上課堂系統在線考試;根據系統自動生成的數據分析，進行針對性講評.

學生活動：在線測試，獨立完成后交流展示，重點展示解題方法，評議錯題.

設計說明? 利用早上課堂系統，實施課堂在線測試，根據系統生成的成績數據統計分析，實時反饋全班學生的作答情況，對正確率低于80%的題目進行針對性講評. 這里設置了有梯度的檢測題，滿足不同層次學生的學習需要，要求學生獨立完成后再交流，口述解題思路，進一步發展學生的邏輯推理能力.

附：課堂考試成績分析統計圖（部分）（見圖8）.

■ 教學反思

課后，筆者對信息技術融合下的數學課堂進行了反思.（1）融合信息技術，有利于充實教學內容，發展學生推理能力.教材以觀察木屋頂框架圖導入，考慮到較多學生可能不熟悉，在教學設計時，補充了部分生活中的三角形圖片，充實了內容，有助于學生通過生活圖例，抽象出具體的三角形圖形，進而理解三角形的概念.考慮到學生數學基礎較好，在學習第二章“相交線與平行線”時，對邏輯推理有了較為嚴謹的書寫格式，所以借助一體機、學生平板，結合幾何畫板和在線測試等，充實了教學內容，豐富了學生的學習方式.結合“由180°，想到什么”，比較自然地引發學生思考，如何通過“引平行線”，結合平行線的性質證明三角形內角和定理，同時借助希沃授課助手同屏展示學生的作答情況，結合師生共同評議，指導學生有條理地表達推理過程，由歸納推理到邏輯推理，較好地發展了學生的邏輯推理能力. （2）傳統的黑板板書不能丟. 雖然信息技術的發展，給課堂教學帶來了很大便利，但要有選擇地合理使用，同時要重視板書設計，結合教學內容，板演分析問題和解決問題的過程，幫助學生更好地理解相關知識. （3）類比角的研究過程，展開對三角形的研究學習，有利于引導學生進一步體驗研究幾何對象的一般思路，為以后繼續類比學習其他幾何對象打好基礎，不斷加深對幾何推理論證的認識.