改進動態規劃算法的移動機器人路徑規劃

周睿慜，李 輝

1.北京科技大學 自動化學院，北京 100083

2.北京科技大學 高級工程師學院，北京 100083

1 引言

隨著移動機器人在交通導航、移動倉庫、游戲設計、特種作業等領域應用的快速增長，移動機器人如何選擇行走路徑，避免碰撞障礙物，快速到達指定目標的路徑規劃問題成為移動機器人研究熱點之一。傳統尋優算法在移動機器人路徑規劃求解中取得了較好的時間效率和路徑結果，如人工勢場法[1]、電勢場法[2]、A*算法[3]、D*算法[4]等。智能優化算法在這個領域的應用研究也較為廣泛，如粒子群算法[5]、遺傳算法[6]、蟻群算法[7-8]等，并通過不斷地融合改進算法，求解結果越來越好[9-11]。這類算法依舊存在局部搜索能力不足，運行時間長，參數設置依賴性高、微調環境穩定性差的問題。動態規劃方法是解決多級決策問題的有效方法，在路徑規劃方面也取得較好的應用成果。文獻[12]依據多機器人系統的動態特征，將圖論知識與動態規劃思想結合解決多機器人路徑規劃。文獻[13]將幾何逼近算法與動態規劃方法結合求解移動機器人路徑規劃。文獻[14]建立自適應動態規劃方法實現輪式機器人非完整運動規劃的最優控制。文獻[15]將動態規劃方法和電勢理論結合規劃無人機三維航跡。由于移動機器人避障環境復雜，動態規劃方法需要與機器人運動路徑特點和障礙物幾何特征相結合運用。本文在格柵環境中分析移動機器人下降路徑搜索過程和上升路徑搜索過程的移動方向變化特點，分別建立兩個搜索過程的動態規劃模型，并提出了一種將兩者結合使用的改進動態規劃算法。該算法能使移動機器人避開障礙，求得到達目標的最優路徑。路徑規劃仿真實驗驗證了改進算法具有計算量小，運行速度快的特點，并可以同時完成多條路徑規劃任務。

2 環境模型的建立

移動機器人路徑規劃是指機器人從現有位置出發自主規避環境中障礙物，到達指定目標的最短或次短移動路徑。本文環境假設為不考慮障礙物的高度，且障礙物為靜態的二維有限空間，利用柵格法建立環境模型。首先以移動機器人的起始點和目標點為對角線畫出矩形區域，作為移動機器人執行任務區域。然后依據機器人半徑尺寸膨脹障礙物，對任務區域進行均勻矩形網格劃分，每個矩形小格記為長寬均為1個柵格單位的矩形柵格。障礙物覆蓋區域柵格用黑色填充，代表不可通行。對于不規則障礙物的未完全覆蓋柵格也全部標黑，不可通行。未覆蓋柵格用白色表示，代表可以通行。圖1 給出25×30 的柵格地圖。移動機器人看作質點，位于地圖左上角的起點，目標點位于地圖右下角。其他情況可以通過圖形的旋轉實現柵格地圖。

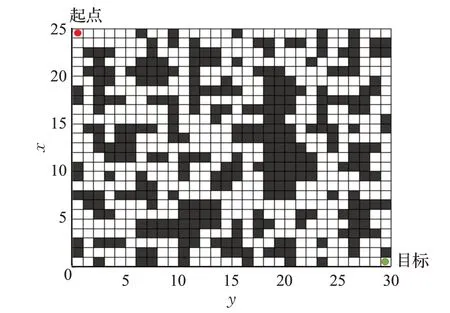
圖1 25×30柵格地圖

3 改進動態規劃算法

3.1 下降路徑搜索動態規劃模型

選取S2中每個柵格為一個階段，柵格位置為狀態變量，移動機器人從當前柵格位置向目標柵格位置靠近過程中移動方向可選為右方、下方和斜下方，如圖2所示，新位置比原位置更接近目標，這個過程稱為下降搜索過程。向右方和正下方移動時移動距離增加1柵格單位長度，向斜下方移動時移動距離增加 2 柵格單位長度。這表明每個階段向目標靠近的決策路徑最多有三種，也表明下降路徑搜索過程是逐步靠近目標的移動過程。

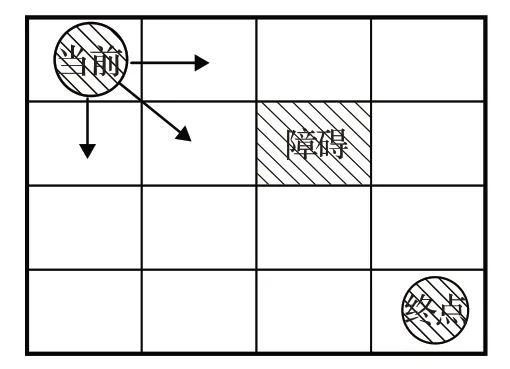
圖2 機器人下降路徑的限定移動方向

設指標函數f(mi,j)(1 ≤i≤N,1 ≤j≤P)為下降路徑搜索動過程移動機器人從m1,1移動到mi,j的最短路徑長度，其取值由f(mi-1,j-1)、f(mi-1,j)、f(mi,j-1)以及移動路徑長度決定。具體定義為：

（1）當mi,j∈S2，mi-1,j和mi,j-1至多一個屬于S1(1 ＜i≤N,1 ＜j≤P)時，令f(mi,j)由式（1）求得函數值，此時存在可移動方向到狀態mi,j，具體情況如圖3所示。

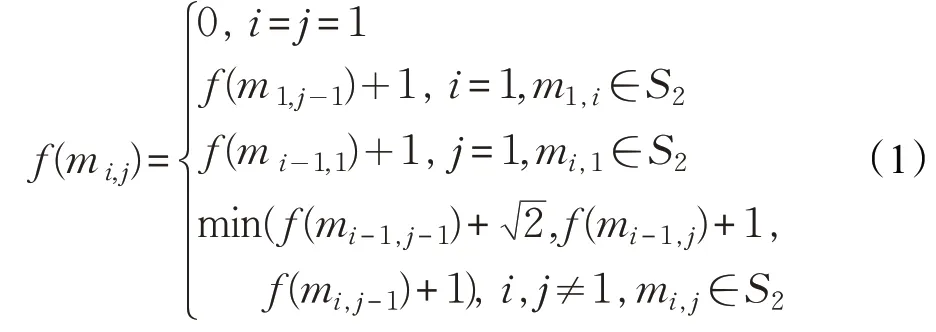
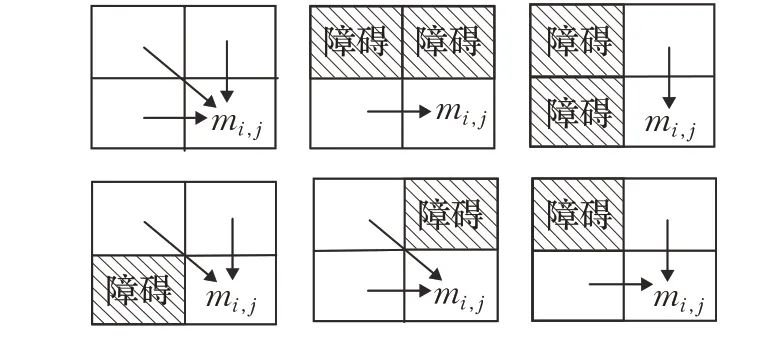
圖3 下降路徑機器人可移動到mi,j 位置的方向

（2）當mi-1,1∈S1，mi,1∈S2(1 ＜i≤N)或mi-1,j∈S1，mi,j-1∈S1(1 ＜i≤N,1 ≤j≤P) 或m1,j-1∈S1，m1,j∈S2(1 ＜j≤P)時，令f(mi,j)等于下降路徑搜索不可到達標記值C2（足夠大的常數值），表示向目標靠近的下降路徑搜索過程中沒有路徑到達狀態mi,j，具體情況如圖4所示。

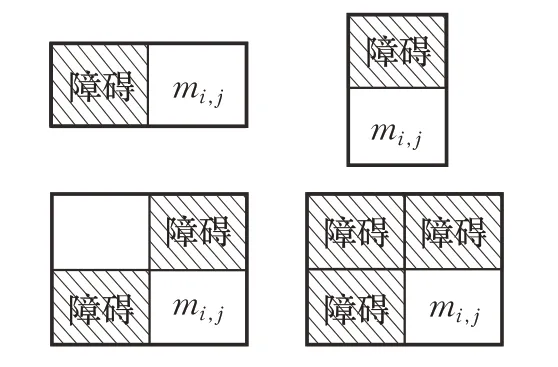
圖4 機器人無可移動到mi,j 位置路徑

為了算法判別方便，對S1中障礙塊的指標值函數值定義為足夠大的常數值C1表示，即當mi,j∈S1(1 ≤i≤N,1 ≤j≤P)時，令f(mi,j)等于障礙值C1。

3.2 上升路徑搜索動態規劃模型

將柵格地圖通過下降路徑搜索動態規劃求得移動機器人到達目標的最優路徑規劃，見圖5（a），稱為單一路徑。柵格環境需要在下降路徑動態規劃中加入上升路徑搜索過程才能避開障礙求得移動機器人到達目標的最優路徑規劃，見圖5（b），稱為混合路徑。上升路徑搜索使移動機器人遠離目標，但可以避開障礙，繼續完成下降路徑搜索動態規劃。接下來，為獲得最小上升路徑建立上升路徑搜索動態規劃模型。

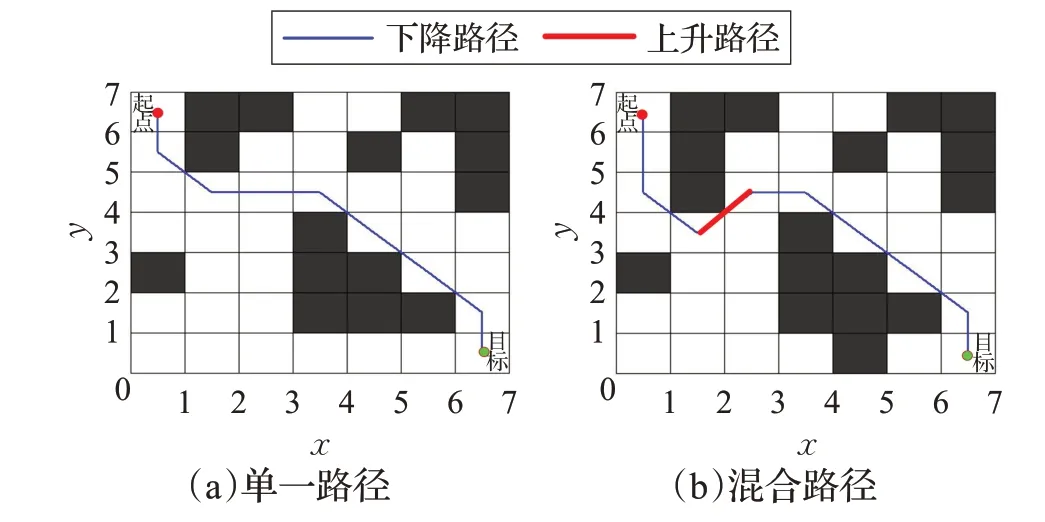
圖5 運動路徑劃分

選取S2中每個柵格為一個階段，柵格位置為狀態變量，此時每個柵格已求得下降路徑搜索動態規劃的指標函數值。設指標函數g(mi,j)(1 ≤i≤N,1 ≤j≤P)為上升路徑搜索動過程移動機器人從m1,1移動到mi,j的最短路徑長度，其取值由g(mi+1,j-1)、g(mi+1,j)、f(mi,j)以及移動路徑長度決定。具體定義為：

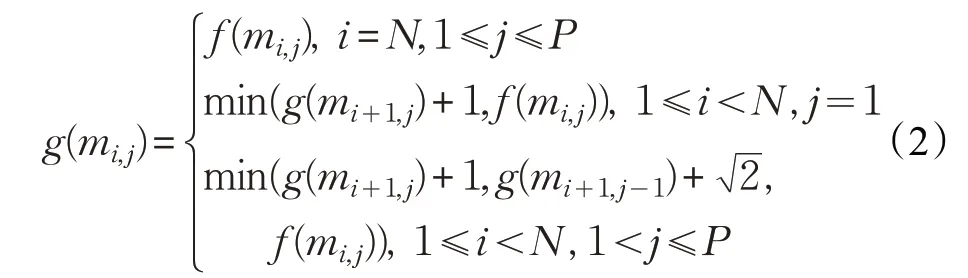
此時可通過上升的可移動方向到達狀態mi,j，具體情況如圖6所示。

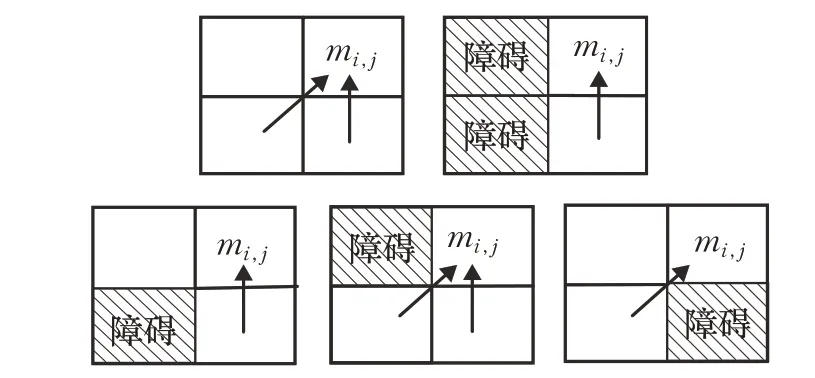
圖6 上升路徑機器人可移動到mi,j 位置的方向

3.3 改進動態規劃算法構建

為獲得混合路徑移動機器人的最優規劃路徑，需要將兩個基本動態規劃模型交互使用，形成改進動態規劃算法。

改進動態規劃算法基本思想是利用下降路徑搜索動態規劃模型逐列求解最優路徑值，當求得某一列元素的最優路徑值均為障礙值C1或下降路徑搜索不可到達標記值C2時，表明通過下降路徑搜索不能到達目標，此時需要引入上升路徑搜索動態規劃模型求解，避開障礙。避障后可繼續進行下降路徑搜索動態規劃求解。因此，改進動態規劃算法是按下降路徑搜索動態規劃每列元素的最優路徑值進行檢測、依據障礙塊分布情況動態交互使用兩個基本動態規劃模型，最終求得移動過機器人到達目標的最短路徑長度。

改進動態規劃算法描述如下：

步驟1賦初值。列值j=1，階段劃分列值k=1，矩陣MN,P存放各階段的最優路徑值，障礙值C1，下降路徑搜索不可到達標記值C2。

步驟2利用下降路徑搜索動態規劃求解j列各元素的最優路徑值M(i,j)(i=1,2,…,N)。

步驟3判別j列的M(i,j)值是否均為障礙值C1或下降路徑搜索不可到達標記值C2。若是轉到步驟5，否則繼續。

步驟4若j=P，輸出M(N,P)最優路徑值，結束算法，否則j=j+1，轉到步驟2。

步驟5從k列到j列利用上升路徑搜索動態規劃求解各列元素的最優路徑值M(i,j)(i=N-1,…,2,1) ，k=j+1，j=j+1，轉到步驟2。

改進動態規劃算法流程圖見圖7。算法占用存儲空間與柵格地圖的維度相同，上升路徑搜索動態規劃的最優路徑值替換原位置存儲值，不增加新的存儲空間，尤其適合二維柵格地圖的路徑規劃問題。兩種基礎動態規劃算法的決策方向選取不超過三個，算法執行的時間效率較好。

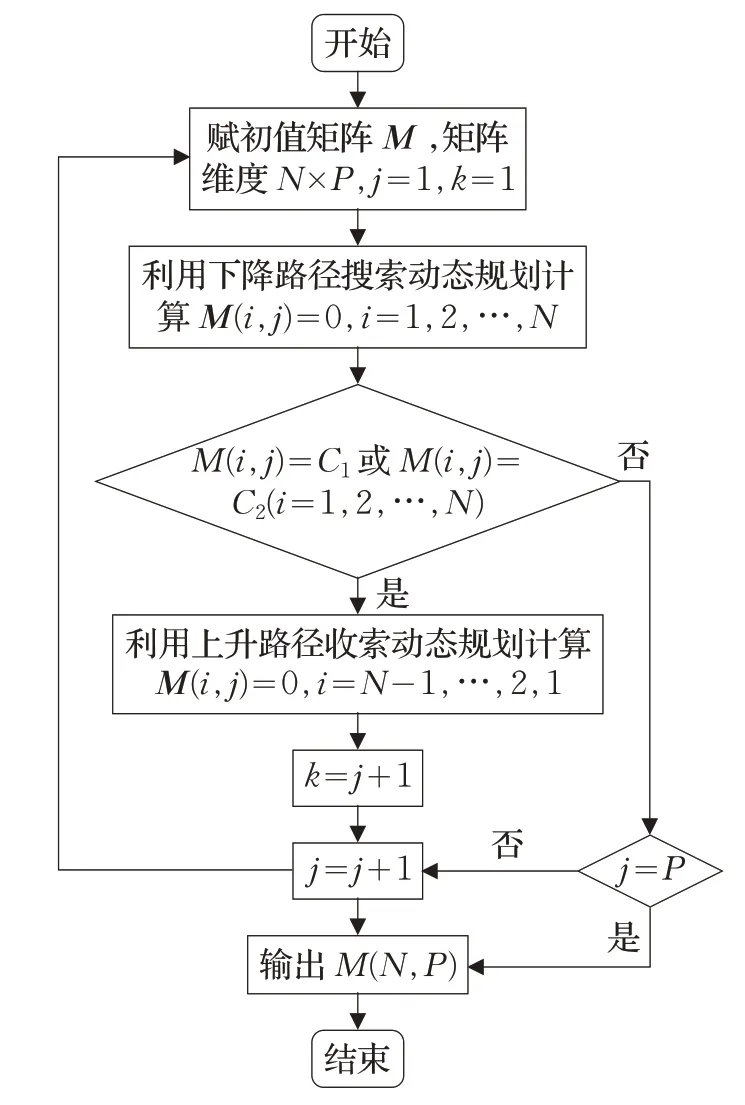
圖7 改進動態規劃算法流程圖

4 仿真實驗結果與分析

為驗證改進動態規劃算法的快速有效性，使用PC機平臺的MATLAB軟件進行編程實現，完成仿真實驗，共進行三組仿真對比實驗。

實驗1 利用格柵法建立25×30柵格地圖，分別取障礙物的覆蓋率為20%、30%、40%和50%作對比實驗。圖8給出了路徑仿真結果，可以看出，不同覆蓋率下算法均能繞開障礙物找到較優路徑且受環境變化影響小。從表1 的數據可知，本文算法能快速找到路徑，且覆蓋率越高，運行時間越短。

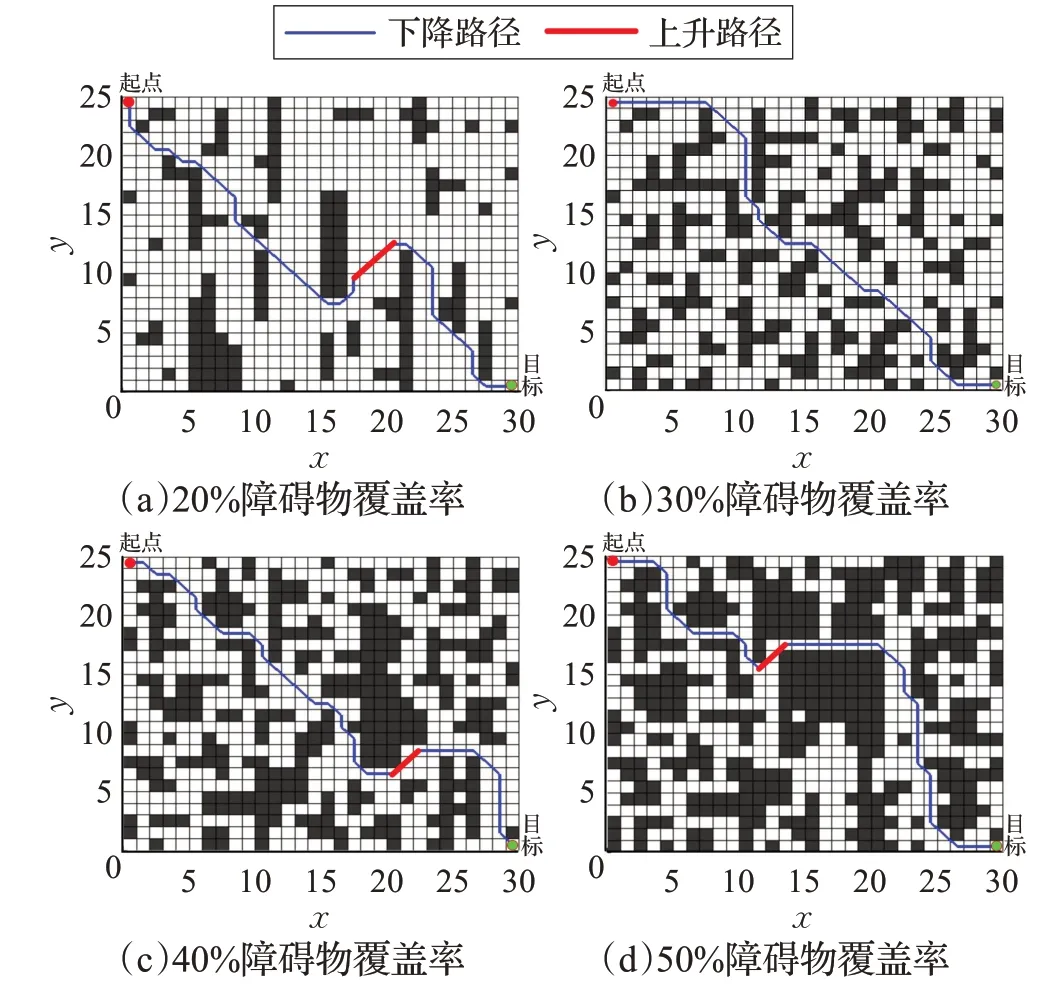
圖8 不同障礙物覆蓋率的路徑仿真

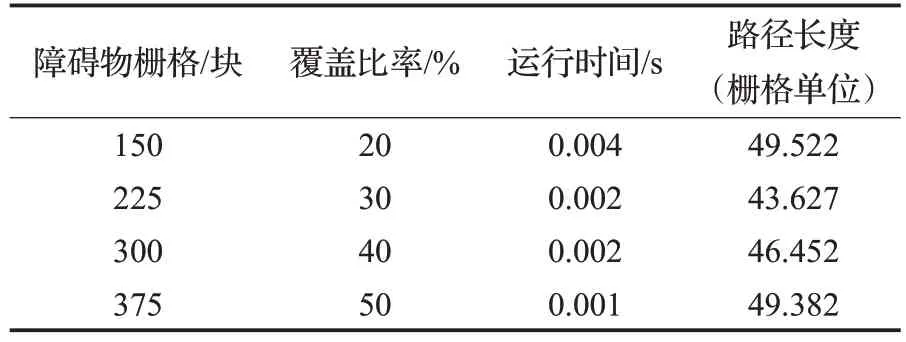
表1 不同障礙物覆蓋率的路徑仿真結果對比

實驗2 改進動態規劃算法同文獻[11]中的改進蟻群算法進行仿真實驗對比。文獻[11]提供了20×20格柵地圖和30×30 格柵地圖的求解算例。用本文算法和文獻中算法進行仿真實驗，移動機器人的運動路徑仿真結果如圖9 所示。仿真結果表明兩種算法的最優路徑長度均為30.384 8（20×20）和42.183 8（30×30），且30×30格柵地圖兩個算法的搜索路徑相同。文獻[11]算法的運行時間為10.142 s（20×20）和42.183 8 s（30×30），本文算法的運行時間為0.002 s（20×20）和0.001 5 s（30×30），可見本文算法能夠快速有效地找到一條較優路徑，并且節省了運行時間。通過算法結構分析可知本文算法避免了多次柵格重新組合，對比迭代更新路徑長度的過程，每個柵格至多賦值兩次，因此時效性好。

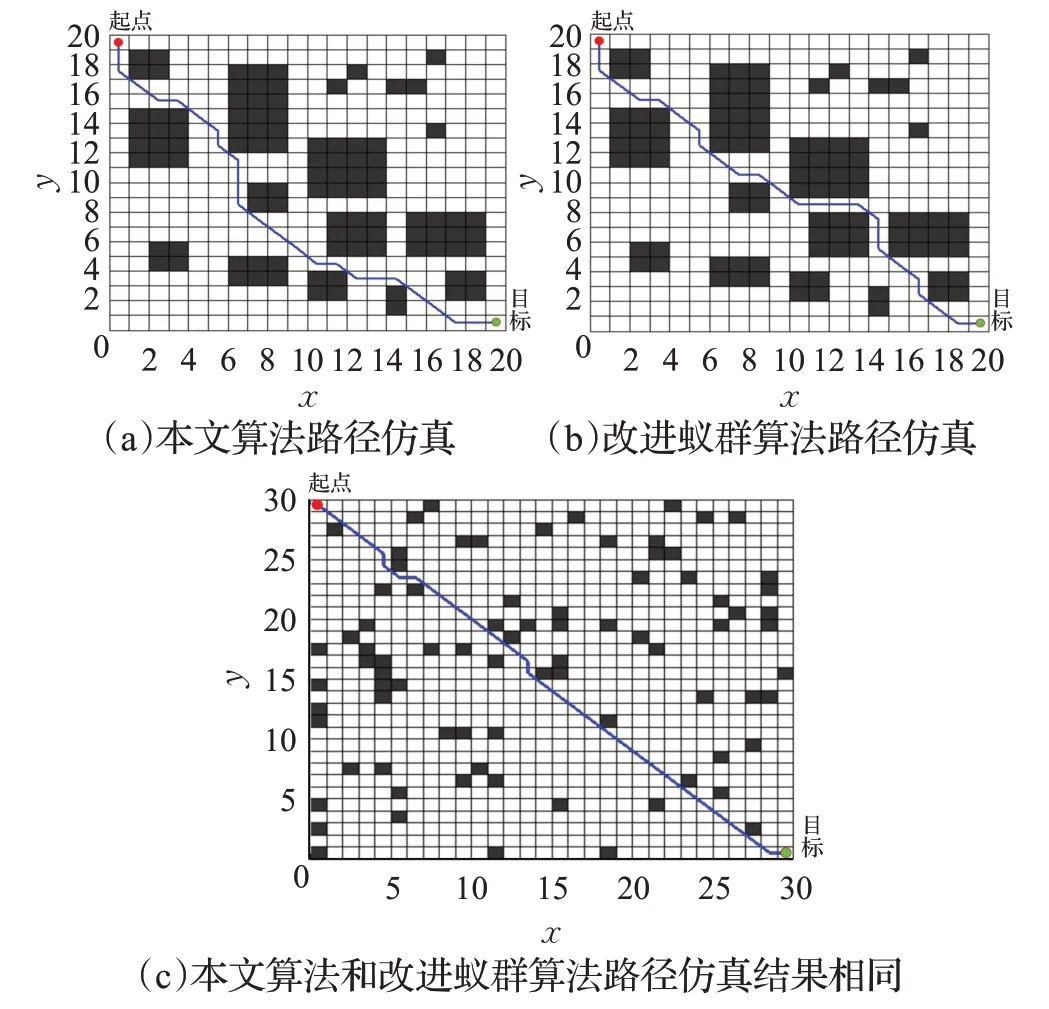
圖9 本文算法與文獻中算法路徑仿真對比

實驗3 利用格柵法建立40×40的柵格地圖，分別選取5 個不同的目標點做仿真實驗。圖10 給出了路徑仿真結果，表2給出改進動態規劃算法求解不同目標點的路徑長度。可以看出，不同目標時算法均能繞開障礙物找到較優路徑，且算法僅需要運行一次，就能找出多個目標點的規劃路徑，總用時為0.007 s。可見本文算法具有承襲性，每個格柵計算值可以用于多個目標點的規劃路徑，且算法的時效性好。

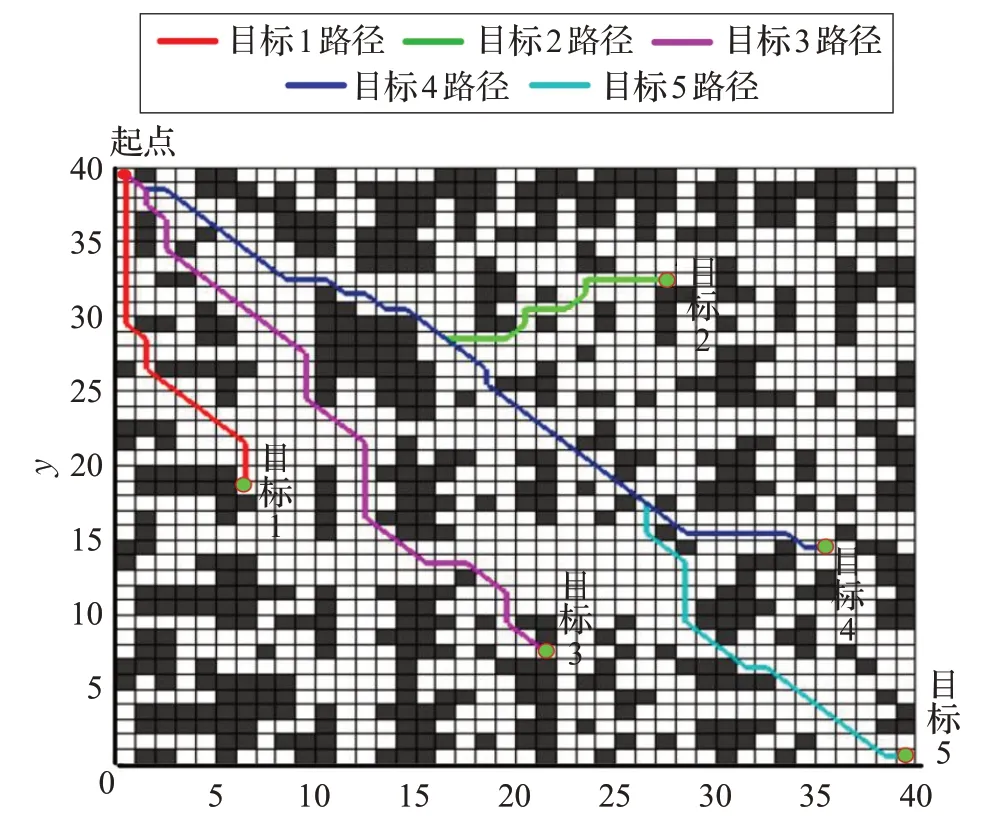
圖10 多目標點的路徑仿真

表2 多目標點的路徑長度結果

5 結論

（1）首次運用兩種動態規劃模型結合使用的方法提出解決移動機器人路徑規劃的改進動態規劃算法。該算法節省反復搜索路徑的時間，為路徑規劃問題求解提供了新思路。

（2）由MATLAB仿真對比實驗可知，本文算法可以同時求得多個目標方向的搜索結果，具有承襲性，能快速求得規劃路徑。與改進蟻群算法相比較在運算時間和最短路徑尋優效果上具一定的優越性，在實際運行過程中，受柵格地圖環境情況影響較小。