點擊高考熱點 再議彈簧模型

河北 康利軍 李會彥

輕彈簧是一個理想化模型，也是高考物理命題中的經典模型。綜合分析近5年的高考物理試題，可見含彈簧模型的試題所占的比重偏高。(如下表)

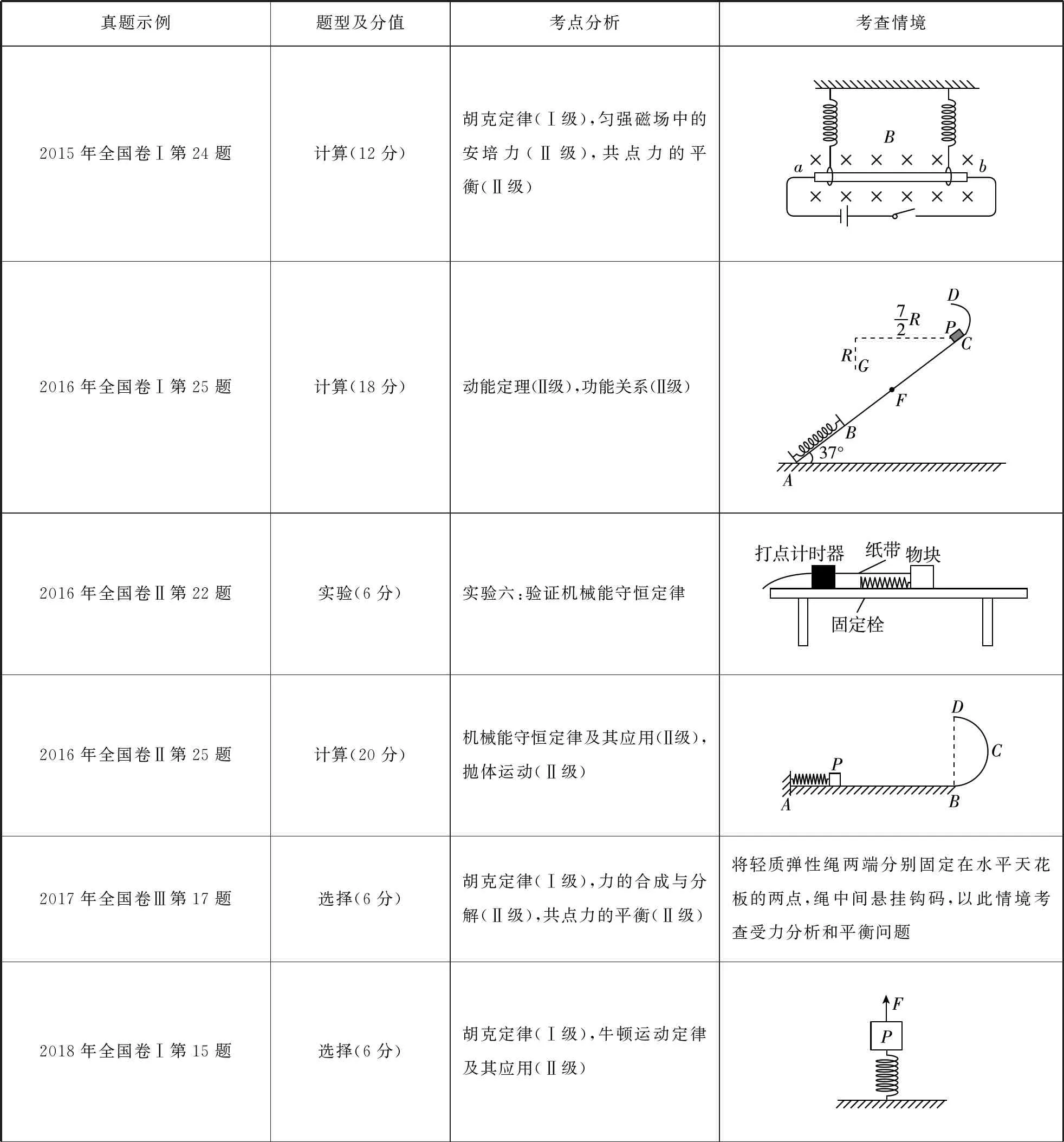
真題示例題型及分值考點分析考查情境2015年全國卷Ⅰ第24題計算(12分)胡克定律(Ⅰ級),勻強磁場中的安培力(Ⅱ級),共點力的平衡(Ⅱ級) 2016年全國卷Ⅰ第25題計算(18分)動能定理(Ⅱ級),功能關系(Ⅱ級)2016年全國卷Ⅱ第22題實驗(6分)實驗六:驗證機械能守恒定律2016年全國卷Ⅱ第25題計算(20分)機械能守恒定律及其應用(Ⅱ級),拋體運動(Ⅱ級)2017年全國卷Ⅲ第17題選擇(6分)胡克定律(Ⅰ級),力的合成與分解(Ⅱ級),共點力的平衡(Ⅱ級)將輕質彈性繩兩端分別固定在水平天花板的兩點,繩中間懸掛鉤碼,以此情境考查受力分析和平衡問題2018年全國卷Ⅰ第15題選擇(6分)胡克定律(Ⅰ級),牛頓運動定律及其應用(Ⅱ級)

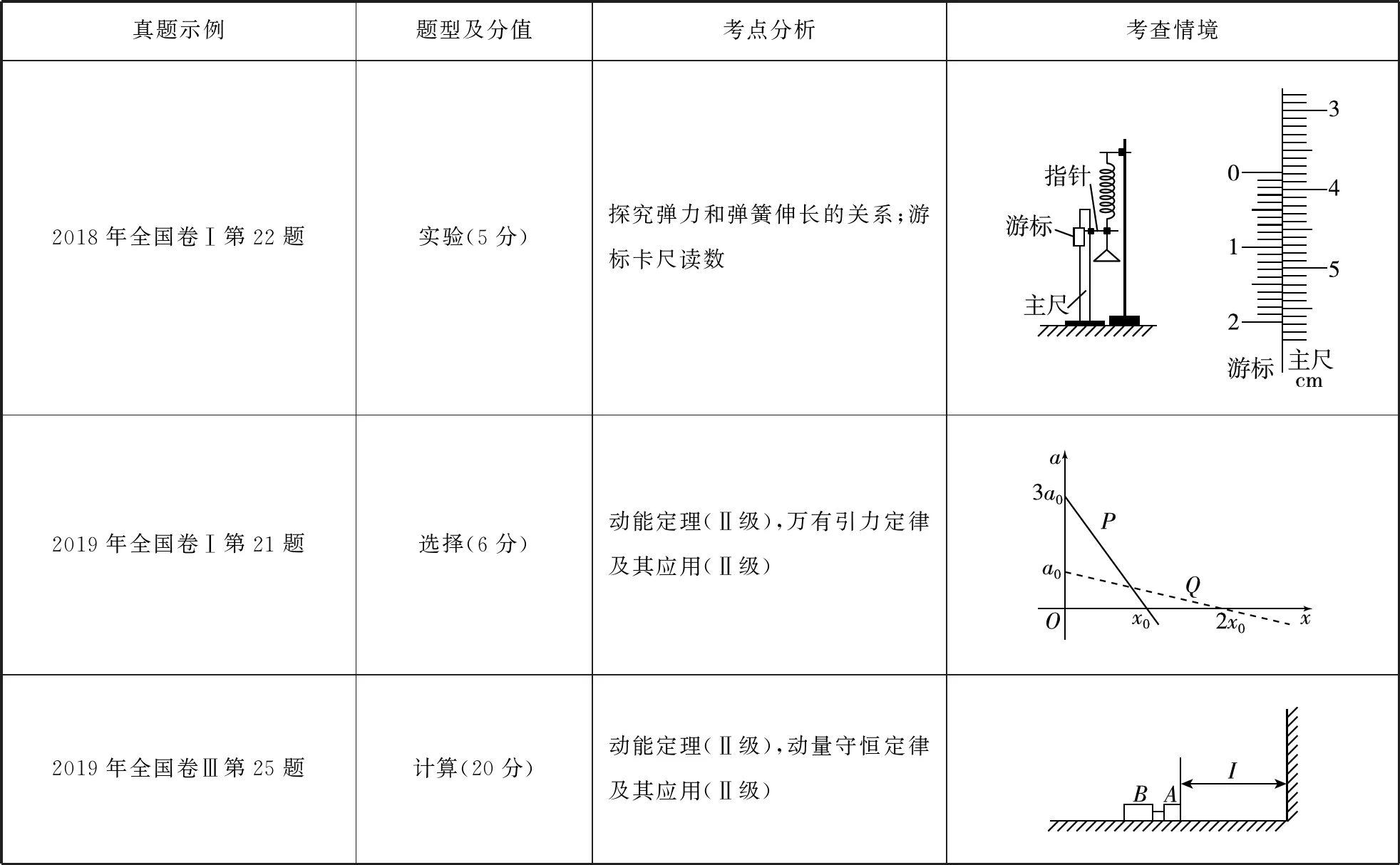
續表

由上可以看出，命題者常以彈簧作為載體，通過彈簧連接滑塊等組成物體系統，對系統或約束或釋放或突變，創設出多樣化的物理情境。

從考點分析上看，彈簧模型可以貫穿到整個高中物理力學知識的體系中。從受力角度看，彈簧的彈力是變力，在空間上，彈簧形變與所接觸物體的位移相關聯，在時間上，彈簧經歷形變需要時間，故彈簧彈力具有與其他力不同的特性；從能量角度看，彈簧是儲存彈性勢能的元件，彈性勢能的表達式在高考《考試大綱》中不做要求，但要靈活應用機械能守恒定律或功能關系來解決彈性勢能的相關問題。所以含彈……