風-波浪荷載對海上風機地震響應的影響

席仁強，許成順，杜修力，許 坤

(1. 北京工業大學城市與工程安全減災教育部重點實驗室，北京 100124；2. 常州大學機械工程學院，江蘇，常州 213164)

目前，投入運營的海上風機大都位于近海，采用固定式平臺，由葉輪-機艙、下部結構和基礎等部分構成[1]，是一種基準周期較長的高聳結構物。固定式海上風機(下文簡稱海上風機)處于風、波浪等復雜海洋動力作用環境。因此，現行海上風電規范[2 ? 4]均建議：分析海上風機地震響應時，考慮常遇風-波浪與設計地震動的組合。

Mardfekri 和Gardoni[5]探討了風-波浪-地震共同作用下單樁式海上風支撐結構的易損性，發現風-波浪荷載增大了結構的破壞概率。Zheng 等[6]以5MW 單樁式海上風機為研究對象，開展了模型試驗，發現波浪作用增大塔頂加速度幅值。Alati等[7]以三腳架、導管架式海上風機為研究對象，分析結構地震響應，發現風-波浪荷載減小塔底彎矩和塔頂位移幅值。Yang 等[8]發現平均風速顯著影響海上風機塔頂位移和結構泥面彎矩幅值。這些研究均表明風-波浪荷載顯著影響海上風機地震響應，但并未得出統一結論。

海上風電場建設時間較短，相關研究較少。對于陸上風機，Asareh 等[9]，Witcher[10]，彭超[11]通過數值模擬發現風荷載增大風力發電機地震響應。Yuan 等[12]發現風荷載降低風力機支撐結構的易損性。Prowell 等[13]針對56 kW 風力發電機開展室外振動臺試驗，發現氣動力減小風力機塔頂加速度和塔底彎矩幅值，但風速僅為5.1 m/s。Yang等[14]發現運行狀態風力發電機的地震響應與平均風速取值有關。席仁強等[15]發現風荷載對風力機地震響應的影響與風速和地震動均有關。這些研究針對陸上風機，其結論不能直接為海上風機所采納。

風-波浪荷載影響海上風機地震響應，為探討其規律、以確定最不利地震荷載組合，本文根據平均風速，通過風-波浪經驗關系確定波浪譜參數；結合單自由度模型和氣動阻尼理論，建立初步分析模型，揭示風-波浪荷載影響海上風機地震響應的機理；隨后，針對單樁式海上風機，基于氣動-伺服-水動-彈性完全耦合方法，通過FAST軟件，分析風-波浪-地震共同作用下結構動力響應，并驗證前述結論。

1 模型與參數

1.1 結構模型

美國可再生能源實驗室(National Renewable Energy Laboratory, NREL)開發了額定功率為5 MW的風力發電機。該風機為3 葉片水平軸風力發電機，輪轂高度87.6 m，葉片長度63 m，采用直徑6 m、壁厚0.06 m 的單樁式基礎，詳細的幾何、物理參數見研究報告[16]。為計算氣動力，塔架分為50 個等長度單元；每個葉片沿軸線從翼根至翼尖分為17 個梁單元，長度依次為：3 個長2.73 m、11 個長4.1 m 和3 個長2.73 m，如圖1 所示。

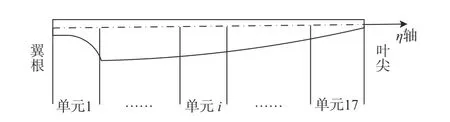
圖1 葉片單元分布圖Fig. 1 Element of blade

采用振型分解法計算塔架和葉片變形，沿塔架、葉片軸線建立局部坐標軸η，泥面、翼根坐標為0，塔頂、翼尖坐標為1。將下部結構和塔架共分為100 個等長度梁單元，單個葉片分為50 個等長度梁單元，采用BMODES 軟件[17]分析海上風機模態。通過Normalized Projection Method 方法，將規格化振型表示為位置η 的6 階多項式。

1.2 風速場模型

為涵蓋停機和運行兩種工作狀態，輪轂高度處10 分鐘平均風速取0 m/s、5 m/s、7 m/s、9 m/s、11.4 m/s、13 m/s、15 m/s、18 m/s、21 m/s、24 m/s。根據IEC 61400?1[3]建議，風廓線采用冪函數，粗糙度指數α 取0.14，平均風速U(ξ)為：

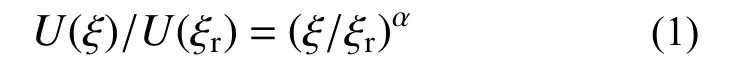
式中：ξ 為高度，以平均海平面為原點，豎直向上為正；ξr為參考高度，取輪轂高度，即為90 m；U(ξr)為參考高度處平均風速。脈動風功率譜采用Kaimal 譜，湍流強度等級為B 類。將風速場總時長取為600 s，利用Turbsim 軟件，生成風速場樣本。

1.3 水動力模型

場地水深為20 m，波浪譜采用JONSWAP譜[18 ? 19]。隨后，根據Ijmuiden 場地觀測數據[20]，可得表1 所列輪轂高度平均風速與波浪譜有效波高HS、譜峰值周期TP關系。此外，跟據DNV[4]建議，假定風、波浪相對各自平均值的變化為獨立變量。

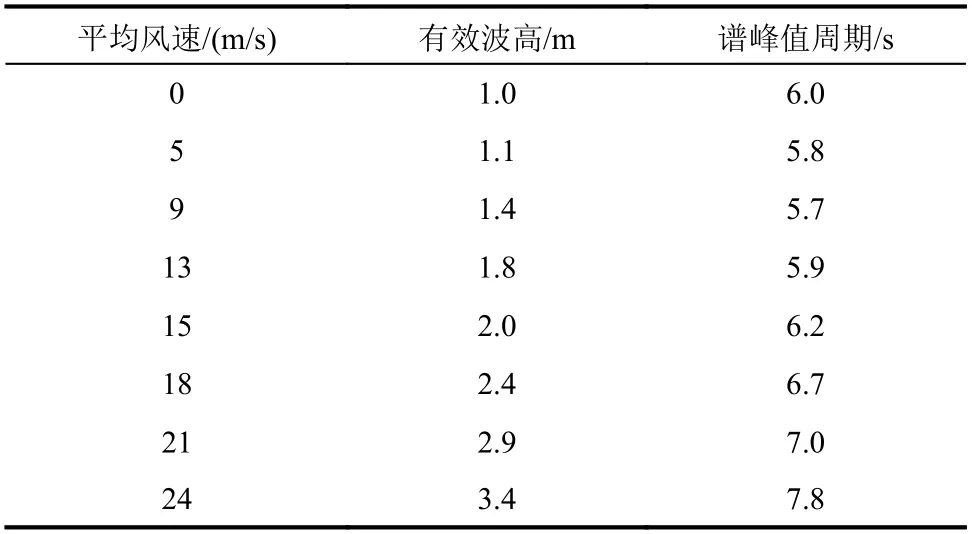
表1 平均風速-波浪關系Table 1 Relationship between wind speed and wave

風-波浪-地震作用下，忽略結構物對波浪的影響，則海上風機受到的動水力可分解為波浪力和地震動引起的附加動水力。采用Morison 公式計算波浪力f：

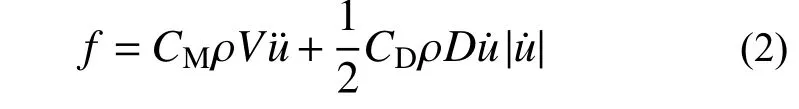
式中：CM為質量系數，取為2.0；CD為拖曳力系數，通常在1.0～1.2 變化，參照文獻[8]，取為1.0；ρ 為水體密度；V為單位高度柱體體積；D為單樁基礎外徑；u˙ 和u¨分別為水質點的運動速度和加速度。

1.4 輸入地震動與地基模型

為表述方便，表2 列出了部分典型荷載組合的特征。為考慮地震動的影響，從PEER 強震數據庫選取一組強震記錄，如表3 所列。對于所選強震記錄，各取一個水平分量作為輸入地震動，Fname 為所選分量的臺站記錄名稱。

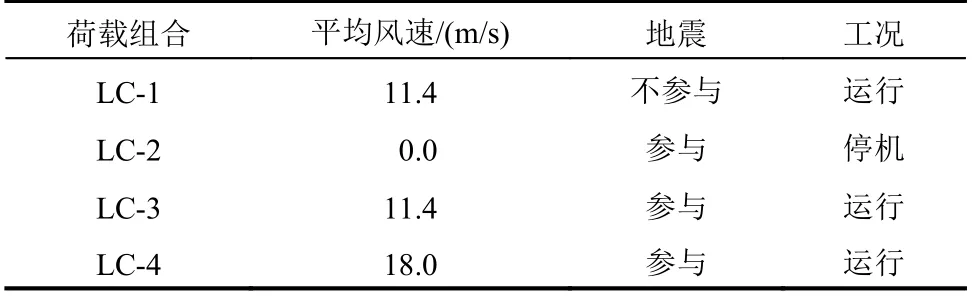
表2 荷載組合Table 2 Loading combination

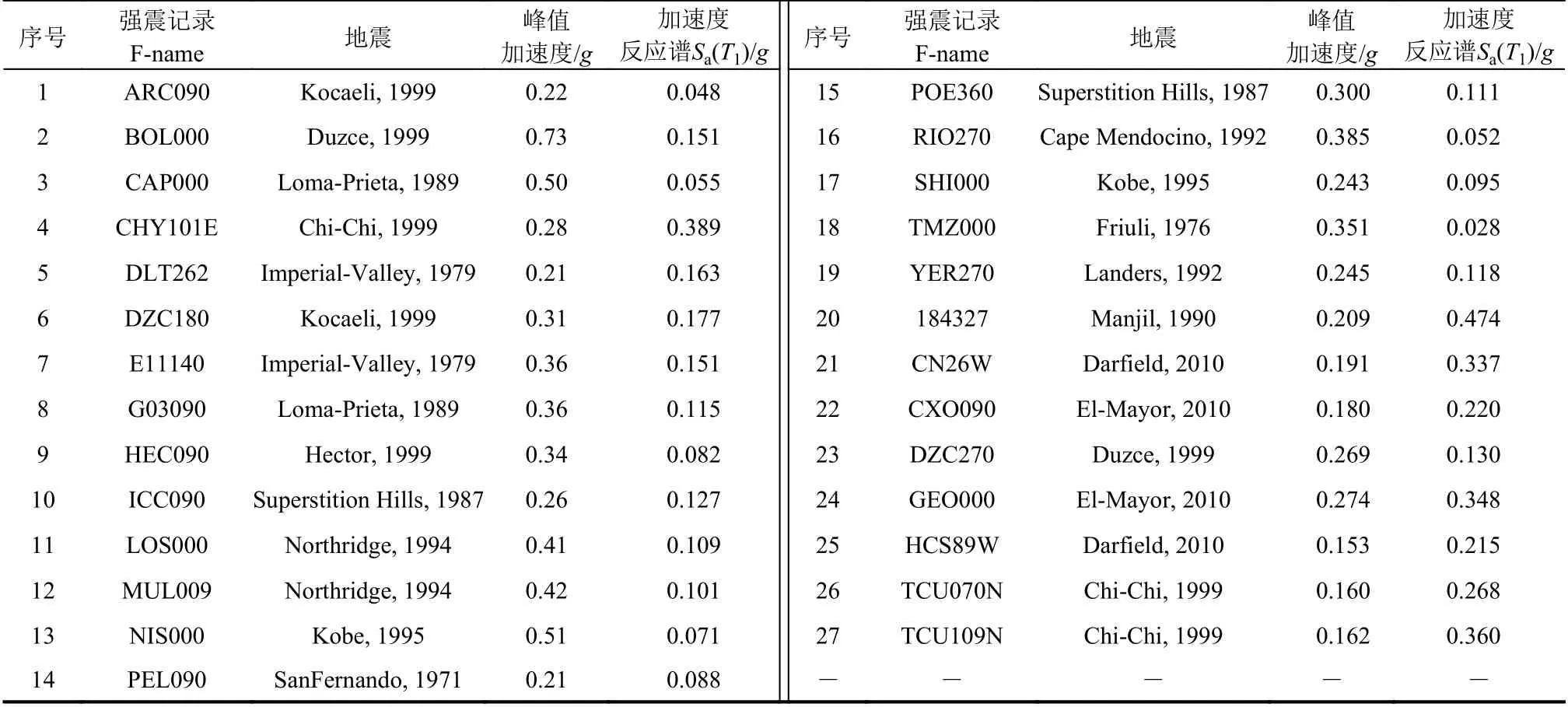
表3 輸入地震動Table 3 Input ground motion

Arany 等[22]發現結構泥面平動、轉動耦合顯著影響海上風機結構動力特性。因此，應采用耦合的線性集中彈簧模擬土-結相互作用。為實現該功能，改動了Asareh 等[9]針對FAST 軟件開發的Seismic 模塊，引入地基剛度矩陣，將Ptlm()函數中的塔底荷載改為：

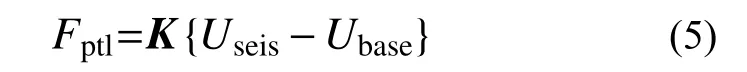
式中：Ubase為下部結構泥面位移；Useis為地震動位移；剛度矩陣K為：

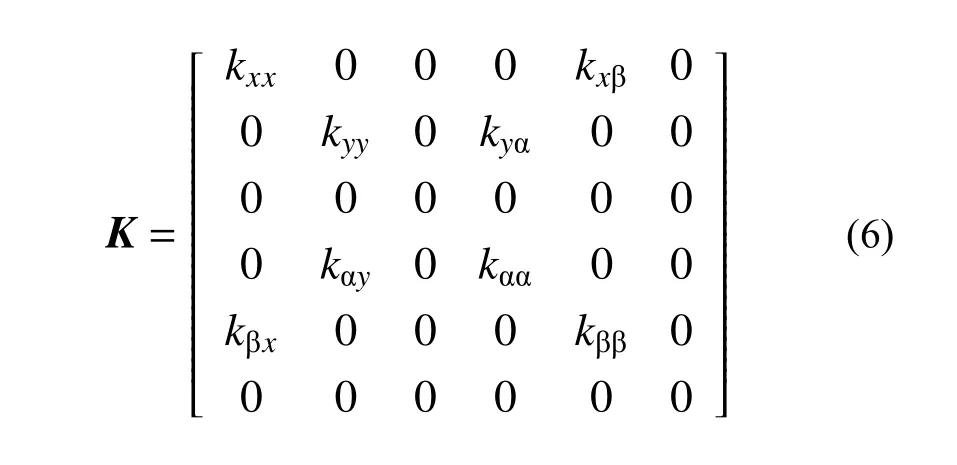
圖2 中γ、Φ 和k0分別為場地土有效重度、內摩擦角和初始剛度系數。針對該場地針和前述單樁基礎，Passon[23]確定了對稱矩陣K的剛度系數：kxx=kyy=2.57×103MN/m;kxβ=?2.25×104MNkαα=kββ=2.63×105MN·m;kyα=?kxβ。

參照文獻[24]的建議，地基阻尼比取為0.8%，與結構阻尼疊加。分析結構地震響應時，計算總時長取600 s，時間步長為0.002 s。為消除初始條件影響，地震動從400 s 時開始。

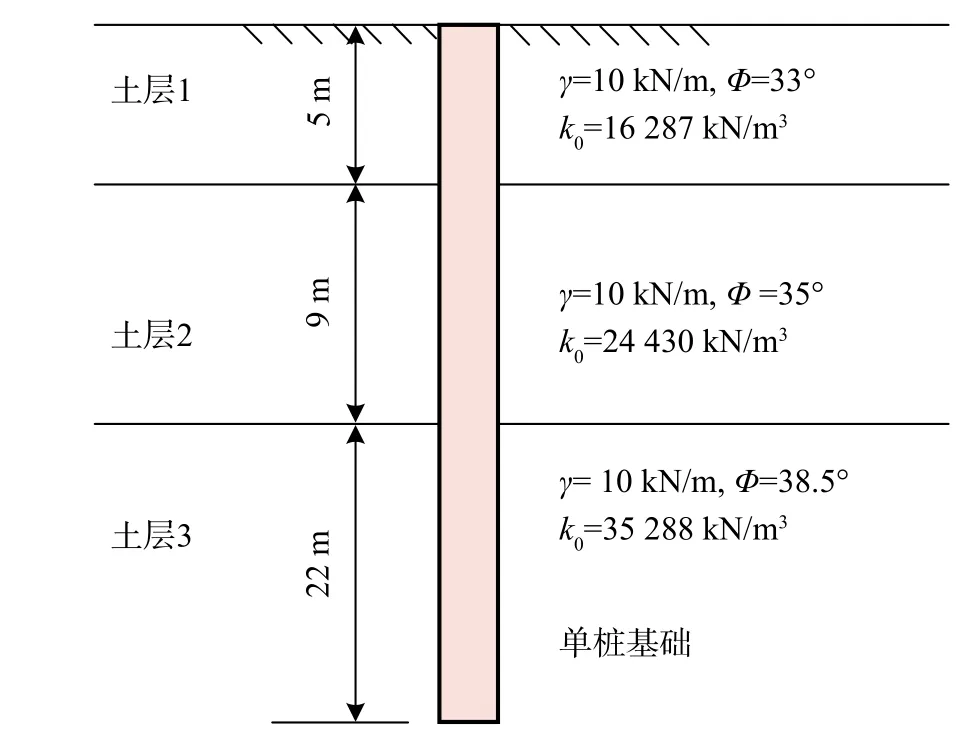
圖2 場地土層分布Fig. 2 Soil layer of site

2 初步分析

風-波浪-地震激勵下，海上風機受到地震荷載、波浪力和氣動力作用。DNV[4]認為波浪輻射阻尼比小于0.15%，Shirzadeh 等[25]發現水體粘滯阻力對單樁式海上風機結構響應的影響不超過5%。為簡化模型，本節忽略水動阻尼及土-結相互作用的影響。

2.1 等效單自由度模型

地震作用下，海上風機發生往復運動。IEC[3]僅考慮一階振型的影響，提出一種等效SDOF 模型。季亮等[26]以有限元法為基準，探討了該模型分析風力發電機地震響應的精度，認為其滿足工程設計需要。該模型假設葉輪為剛體，如圖3 所示，其運動方程為：

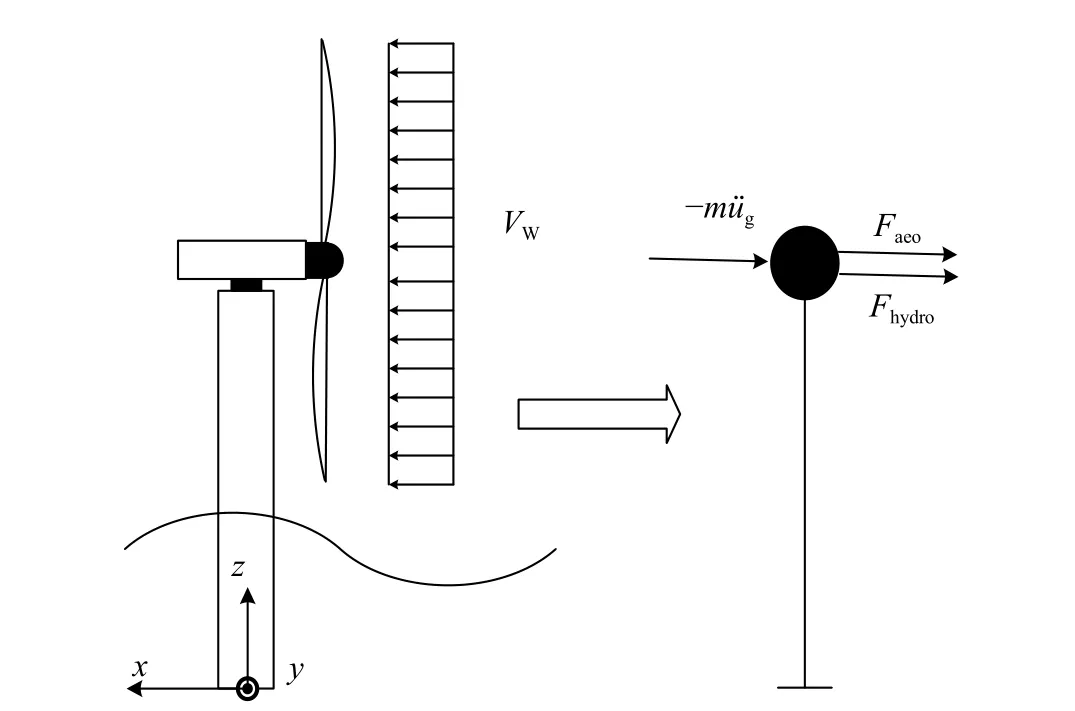
圖3 分析模型Fig. 3 Analysis model

2.2 風-波浪荷載對地震響應的影響

針對NREL 5MW 單樁式海上風機，假定系統受穩態風作用，風速取為11.4 m/s，根據葉素動量理論[30]，FaWeo為700 kN。此時，氣動阻尼比取0.07，結構阻尼比取0.01，系統自振頻率取0.29 Hz。通過式(2)計算波浪力，根據支撐結構基準振型，可得等效波浪力如圖4 所示，顯然，等效波浪力遠小于氣動力。采用不同輸入地震動，計算海上風機塔頂位移響應，如圖5 所示。

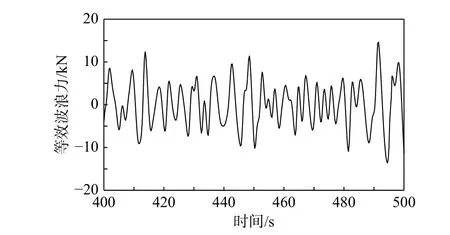
圖4 等效波浪力Fig. 4 Equivalent wave force

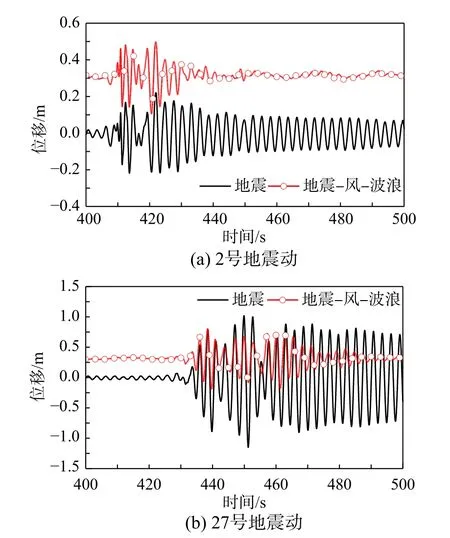
圖5 不同地震動激勵下海上風機塔頂位移時程Fig. 5 Tower-top displacement excited by different earthquakes

輸入地震動為2 號強震記錄時，風-波浪-地震作用下海上風機塔頂位移的峰值大于地震單獨作用。此時，氣動阻尼耗散的能量小于風-波浪對海上風機所做功，風-波浪增大結構位移的幅值，表現出動荷載作用，與Mardfekri 和Gardoni[5]的發現一致。

輸入地震動為27 號強震記錄時，風-波浪-地震作用下海上風機塔頂位移的峰值小于地震單獨作用。此時，氣動阻尼耗散的能量超過風-波浪對風力發電機所做功，風-波浪減小結構位移的幅值，具有阻尼效應，和Alati 等[7]的發現相同。

風-波浪通過氣動荷載、波浪力和氣動阻尼影響海上風機地震響應。本節采用SDOF 模型，發現風-波浪對海上風機地震響應的影響與地震動強弱有關，然而，未考慮葉片變形及控制系統的影響。為驗證初步分析結果，定量評估風-波浪的影響，第3 部分通過數值模擬分析海上風機地震響應，揭示風-波浪荷載影響結構響應的規律。

3 數值模擬結果與討論

NREL 結合多體動力學和振型分解法，開發了風力發電機氣動-伺服-彈性耦合分析軟件FAST[31]。經過其他研究者開發，該軟件能夠分析風力發電機地震響應[9]，其可靠性也得到了驗證[13]。為考慮土-結相互作用影響，采用1.4 節模型，對FAST軟件進行二次開發。為驗證其有效性，針對NREL 5 MW 海上風機，分析了支撐結構前后向1 階、2 階振型的頻率，如表4 所示。因此，采用FAST軟件分析風-波浪-地震作用下海上風機動力響應是可靠的。

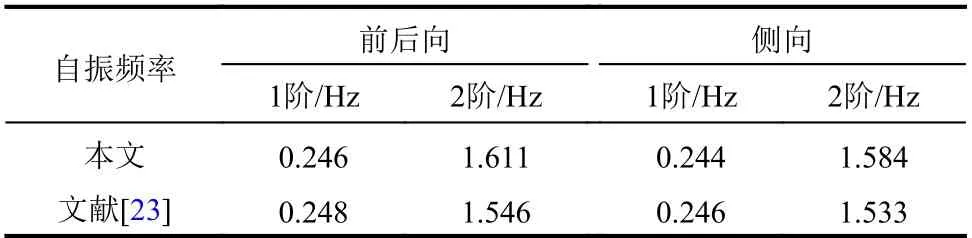
表4 支撐結構振型頻率Table 4 Natural frequencies of support structures

3.1 結構地震響應特性

考慮風速場的隨機性，對于每個平均風速生成多個風速場樣本。不同風-波浪組合作用下，海上風機下部結構泥面彎矩和塔頂位移幅值如圖6、圖7 所示。平均風速等于額定風速(11.4 m/s)時，結構泥面彎矩的幅值最大，為100 MN·m。平均風速超過額定值，為保證結構安全，控制系統執行變槳距操作，結構泥面處彎矩下降。塔頂位移幅值隨平均風速的變化規律與泥面彎矩類似。氣動力合力作用于海上風機塔頂附近，因此，平均風速變化對結構響應具有顯著影響。

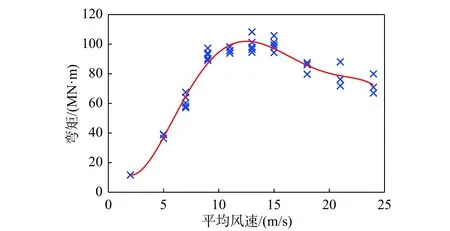
圖6 風-波浪作用下結構泥面彎矩幅值Fig. 6 Maximum mudline moment of support structure excited by wind-wave loading

圖7 風-波浪作用下塔頂位移幅值Fig. 7 Maximum tower-top displacement excited by wind-wave loading

表3 中1 號地震動的加速度時程如圖8 所示，采用第1 節的模型及參數，分析海上風機地震響應。圖9 為塔頂位移時程，t=400 s 時，地震發生，風-波浪-地震共同作用時(LC3)，塔頂位移的峰值大于地震單獨作用(LC2)，風-波浪總體表現出動荷載作用，與Mardfekri 和Gardoni[5]的發現一致。

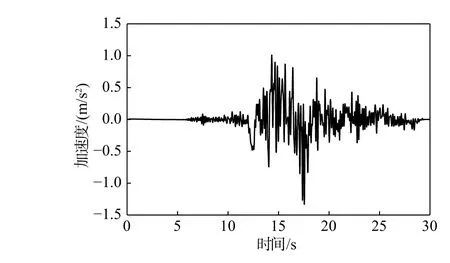
圖8 ARC 波加速度時程Fig. 8 Acceleration time history of ARC wave

圖9 輸入ARC 波的塔頂位移響應Fig. 9 Tower-top displacement when earthquake is ARC wave

根據圖9，對于荷載組合LC3，t=430 s，地震結束，氣動阻尼使得塔頂位移振幅迅速衰減；t>440 s，塔頂位移時程與風-波浪單獨作用(LC1)基本一致。對于荷載組合LC2，由于不存在氣動阻尼，地震結束后，塔頂位移振幅衰減緩慢。

圖10 為下部結構泥面處彎矩時程。t=400 s，地震發生，在強震持續階段，風-波浪表現出動荷載作用：風-波浪-地震作用下(LC3)，泥面彎矩的峰值大于地震單獨作用(LC2)。對于荷載組合LC3，地震結束后，彎矩振幅迅速衰減；t>440 s，泥面彎矩時程與LC1 基本一致。對于荷載組合LC2，由于不存在氣動阻尼，t>440 s，彎矩振幅衰減較慢。

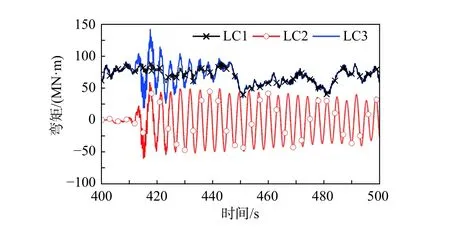
圖10 輸入ARC 波的塔底彎矩Fig. 10 Mudline bending moment of support structure

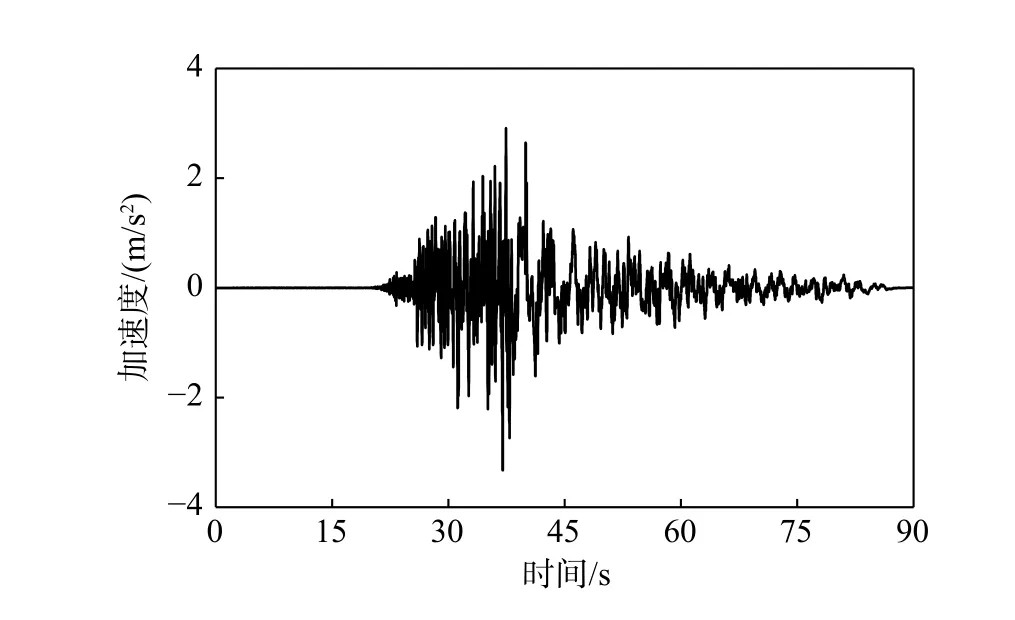
圖11 CHY 波加速度時程Fig. 11 Acceleration time history of CHY wave

平均風速超過額定風速后，控制系統執行變槳距操作，氣動力減小，因此，荷載組合LC3 作用下，塔頂位移幅值大于LC4，如圖13 所示。同時，對于荷載組合LC2，風力機處于停機狀態，氣動阻尼可以忽略，t>500 s，地震結束，塔頂位移振幅衰減緩慢；強震持續階段，由于系統阻尼小于荷載組合LC3 和LC4，因此，塔頂位移的峰值最大。這一結果表明：氣動阻尼減小了塔頂位移的峰值，風-波浪作用總體表現出阻尼效應。

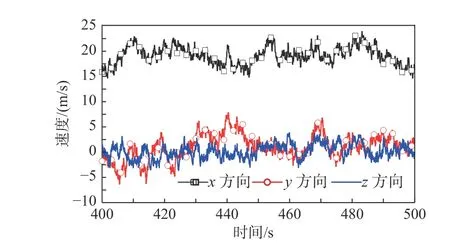
圖12 風速時程Fig. 12 Time history of wind speed

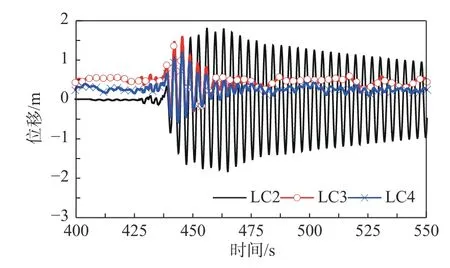
圖13 輸入CHY 波的塔頂位移Fig. 13 Time history of tower-top displacement

圖14 為下部結構泥面彎矩時程，三種荷載組合作用下，彎矩響應特征與塔頂位移類似。LC3作用下，結構泥面彎矩的峰值大于LC4。停機狀態，由于系統阻尼小，結構泥面彎矩的峰值在三種荷載組合中最大。因此，氣動阻尼減小了結構泥面彎矩的峰值，風-波浪作用總體表現出阻尼效應。

根據以上兩個算例，風-波浪荷載對海上風機地震響應同時具有動荷載作用和阻尼作用，總效應與輪轂高度處平均風速、地震動均有關。

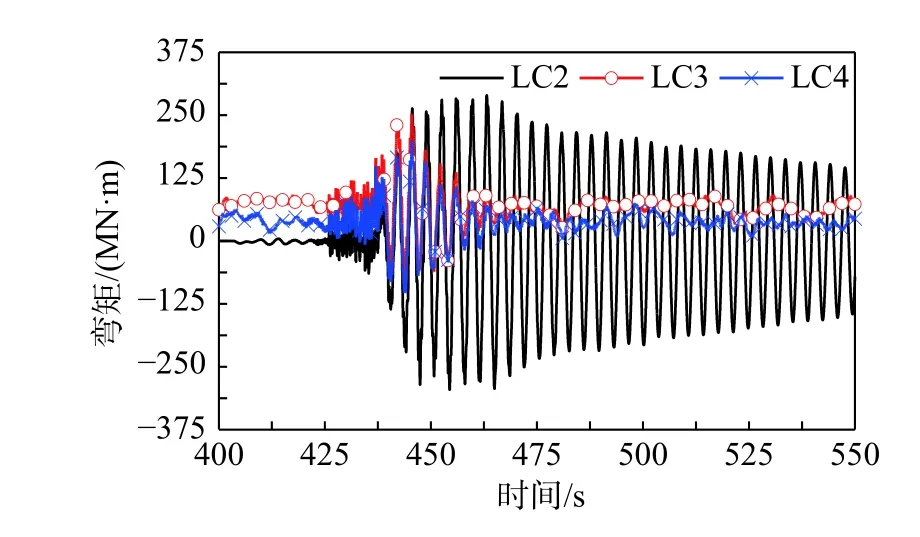
圖14 輸入CHY 波的塔底彎矩Fig. 14 Mudline bending moment of support structure

3.2 平均風速的影響

為進一步探討風-波浪對海上風機地震響應的影響，定義結構響應放大系數φ：

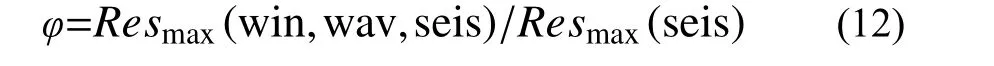
式中，Resmax(win,wav,seis)和Resmax(seis)分別為風-波浪-地震共同作用、地震單獨作用下海上風機響應的峰值。φ大于1，表示風-波浪荷載增大結構響應幅值；小于1，則代表其減小響應幅值。為探討結構響應特征，下文將塔頂位移峰值、加速度峰值和泥面剪力峰值、彎矩峰值代入式(12)，得到相應位置的位移、加速度、剪力和彎矩放大系數。

為消除風速場隨機性的影響，參照Santangelo等[32]的做法，對每個平均風速生成5 個樣本；然后，各樣本與地震動組合，分析海上風機動力響應；最后，將結構響應幅值平均，得到風-波浪-地震共同作用下結構幅值。根據式(12)，可得塔頂位移、泥面剪力和彎矩響應放大系數如圖15～圖17 所示。

圖15 為塔頂位移放大系數。由于該型海上風機采用了變槳距控制，對于不同的地震動，風-波浪-地震共同激勵下，輪轂高度處平均風速等于額定風速時，塔頂位移放大系數最大。

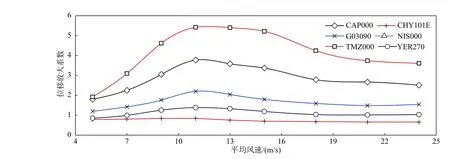
圖15 不同平均風速的塔頂位移放大系數Fig. 15 Displacement magnification factor of tower-top with different mean wind speed

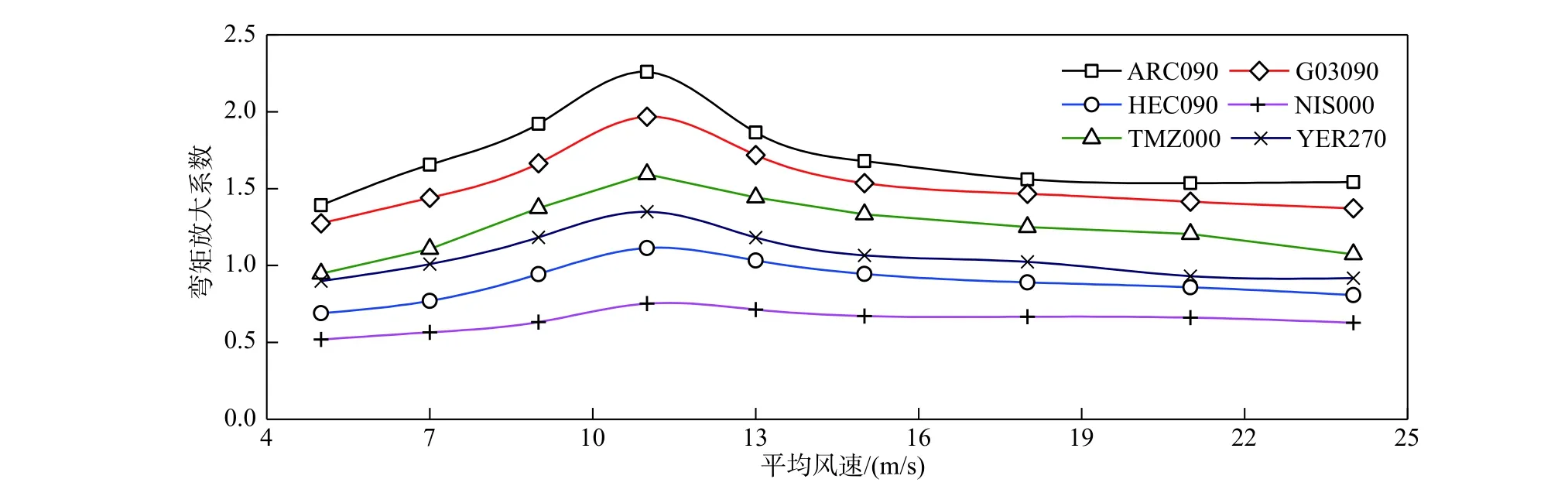
圖16 不同平均風速的結構泥面彎矩放大系數Fig. 16 Mudline bending-moment magnification factor of support structure with different mean wind speed

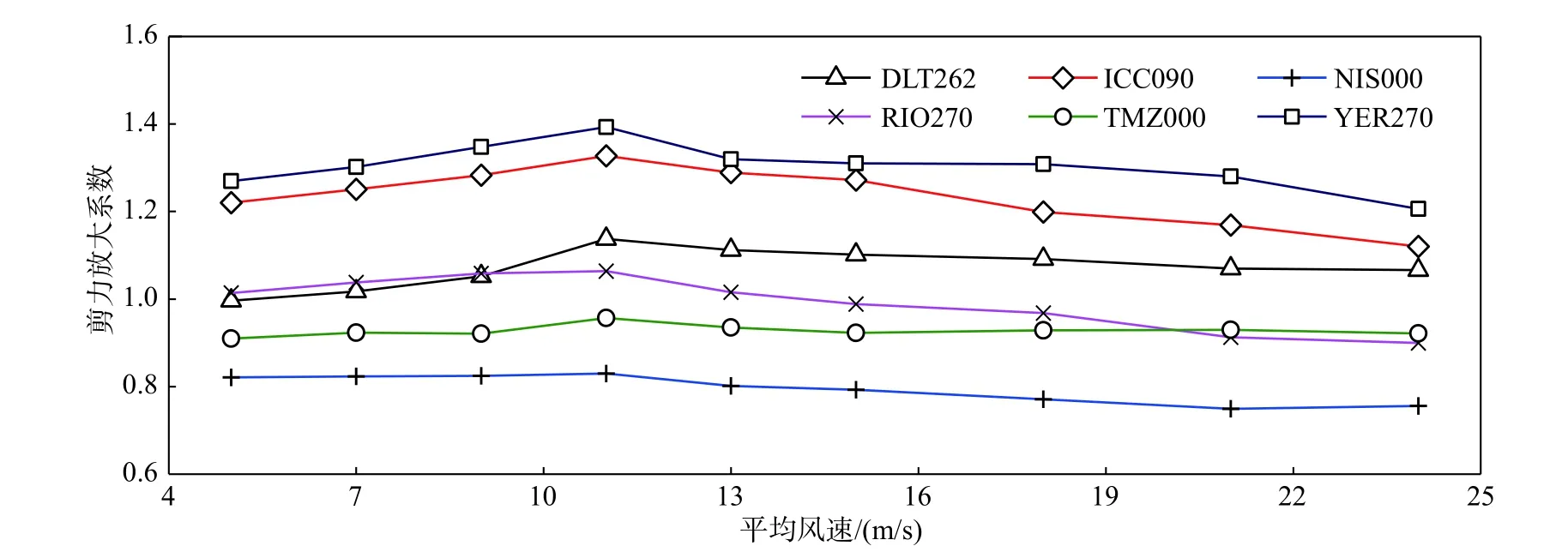
圖17 不同平均風速的結構泥面剪力放大系數Fig. 17 Mudline shear-force magnification factor of support structure with different mean wind speed

圖16 為下部結構泥面彎矩放大系數，平均風速等于額定風速時，取最大值。風-波浪-地震作用下，海上風機結構泥面彎矩和塔頂位移的峰值由葉輪氣動力和結構慣性力控制，且氣動力作用于塔頂附近，因此，輪轂高度處平均風速值對塔頂位移、泥面彎矩的峰值具有顯著影響。圖17 為下部結構泥面剪力放大系數，對于所有地震動，平均風速等于額定風速時，其值最大，該特征與塔頂位移和泥面彎矩相同。

總體而言，風-波浪-地震共同作用下，變槳距控制對海上風機響應具有顯著影響。輪轂高度處平均風速值等于額定風速時，結構泥面處內力和塔頂運動的峰值最大，此時，荷載組合LC2 是海上風機的最不利荷載。

3.3 地震動的影響

根據3.1 節結論，輪轂高度處平均風速等于額定風速時，結構響應的峰值最大。為驗證初步分析結果，平均風速取11.4 m/s，與波浪-地震組合，分析海上風機響應。單樁式海上風機支撐結構以泥面附近截面彎曲破壞為主[5]，為兼顧機艙內設備安全，選取下部結構泥面彎矩、剪力和塔頂位移、加速度作為響應指標。根據式(12)可獲得這些參數的響應放大系數，如圖18～圖21 所示，并給出趨勢線方程。總體而言，隨地震動加速度反應譜值增大，這些參數的放大系數遞減。為揭示風-波浪荷載影響海上風機地震響應的規律，采用結構基準周期對應地震動加速度反應譜值區分地震動，并表征其強弱。

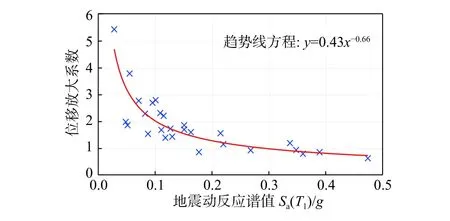
圖18 塔頂位移放大系數Fig. 18 Displacement magnification factor of tower-top

圖19 塔頂加速度放大系數Fig. 19 Acceleration magnification factor of tower-top

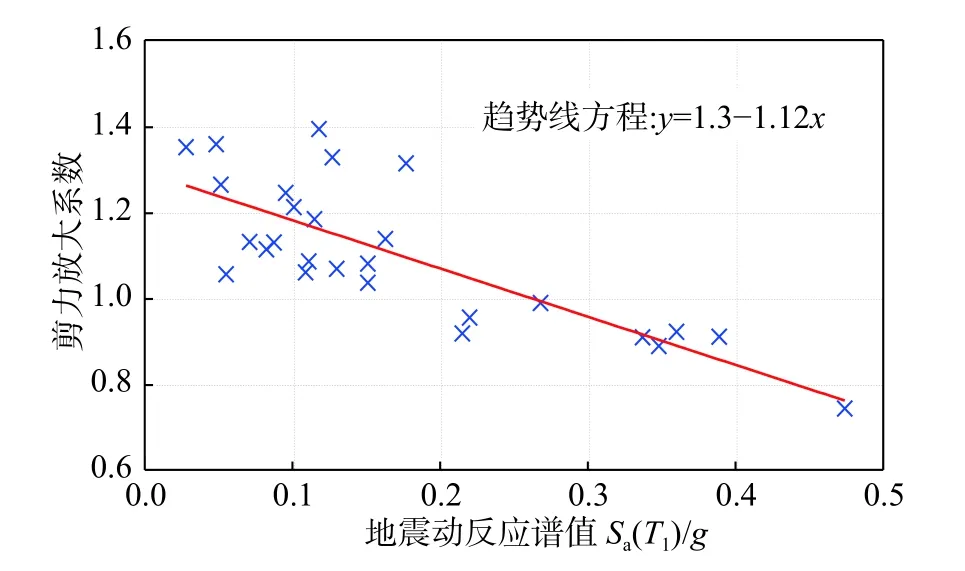
圖20 泥面彎矩放大系數Fig. 20 Mudline moment magnification factor of support structure

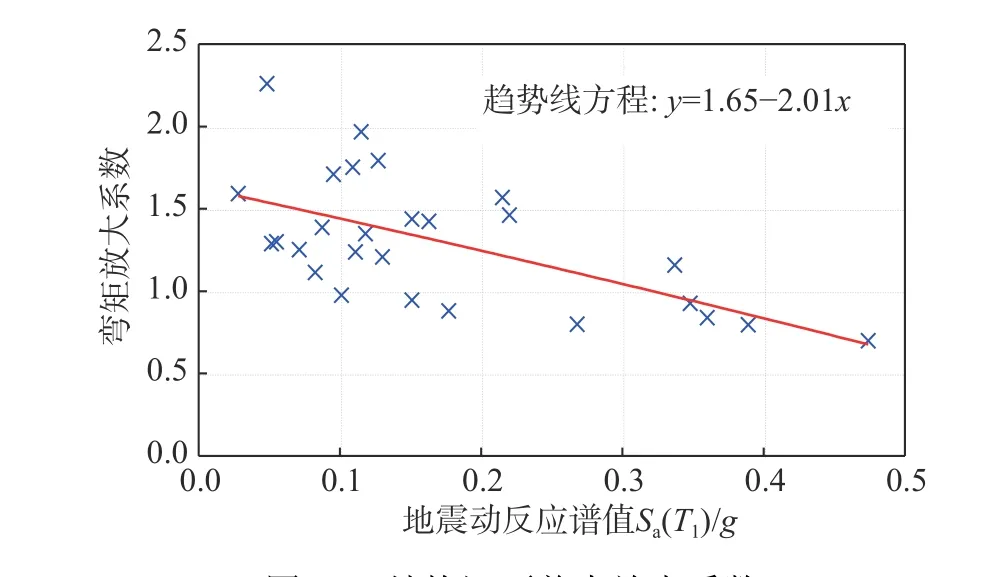
圖21 結構泥面剪力放大系數Fig. 21 Mudline shear magnification factor of support structure

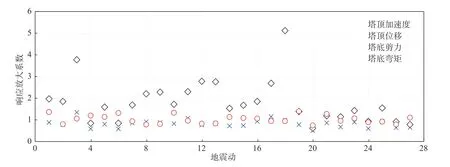
圖22 海上風機響應放大系數Fig. 22 Response magnification factor of OWTs

根據圖18，加速度反應譜值小于0.25g時，塔頂位移放大系數大于1，即風-波浪荷載增大塔頂位移的峰值；加速度反應譜值大于0.25g時，塔頂位移放大系數小于1，風-波浪荷載減小塔頂位移的峰值。因此，風-波浪對塔頂位移響應的影響與地震動有關，弱震作用下，風-波浪增大塔頂位移幅值，表現出動荷載效應；強震作用下，風-波浪減小塔頂位移幅值，具有阻尼效應。根據圖19，弱震作用下，風-波浪增大塔頂加速度幅值；強震作用下，風-波浪減小塔頂加速度幅值。

根據圖20，加速度反應譜值小于0.3g時，結構泥面彎矩放大系數大于1，即風-波浪增大泥面彎矩的峰值；加速度反應譜值大于0.3g時，泥面彎矩放大系數小于1，風-波浪減小泥面彎矩的峰值。圖21 為下部結構泥面剪力放大系數，與泥面彎矩峰值類似，地震較弱時，風-波浪增大泥面剪力的峰值；地震較強時，風-波浪減小泥面剪力的峰值。

圖22 為平均風速等于額定風速時的結構響應放大系數。整體而言，風-波浪荷載對結構彎矩、位移峰值的影響顯著超過剪力和加速度。氣動力合力作用于塔頂附近，顯著影響塔頂位移和結構泥面彎矩的峰值。結構加速度響應取決于高頻激勵，而氣動力和波浪力以低頻為主，因此，其對塔頂加速度峰值的影響較小。同時，結構響應放大系數與輸入地震動有關。以塔頂位移為例，弱震激勵下，風-波浪增大其峰值。因此，風-波浪荷載不變時，地震動越弱，位移放大系數越大。根據表3，3 號和18 號地震動加速度反應譜值分別為0.055g和0.028g，因此，對應的位移放大系數顯著大于其他地震動。

綜上所述，弱震作用下，風-波浪荷載增大海上風機結構泥面內力和塔頂運動的峰值，具有動荷載效應；強震作用下，風-波浪減小海上風機結構泥面內力和塔頂運動的峰值，表現出阻尼效應。塔頂位移和加速度峰值、結構泥面剪力和彎矩峰值受不同地震動分量控制，動水力和氣動力的貢獻也不相同。因此，對于不同的結構響應參數，難以確定統一的強、弱震界限。

4 結論與展望

通過初步分析和數值模擬，揭示了風-波浪對海上風機地震響應的影響機理。根據塔頂位移和加速度、結構泥面剪力和彎矩響應特征，探討了風-波浪荷載對海上風機地震響應的影響，得出以下結論：

(1) 風-波浪對海上風機地震響應的影響由其氣動阻尼和動荷載效應共同決定。氣動阻尼耗散的結構動能與地震強度有關；而動荷載效應取決于平均風速值。因此，風-波浪荷載對海上風機地震響應的影響與平均風速和地震均有關。

(2) 變槳距控制策略使得海上風機所受氣動力隨輪轂高度平均風速呈非單調變化。數值分析結果表明：對于運行狀態的海上風機，風-波浪-地震共同作用下，平均風速等于額定風速時，塔頂運動和泥面內力的峰值最大。

(3) 對于運行狀態的海上風機，弱震作用下，風-波浪表現出動荷載效應，增大結構泥面處內力和塔頂運動峰值，增加結構破壞風險；強震作用下，風-波浪具有阻尼效應，減小塔底內力和塔頂運動幅值，能夠提高結構可靠性。

(4) 海上風機結構響應受不同因素控制，塔頂加速度幅值由地震動控制，下部結構泥面處彎矩和塔頂位移的峰值由風、波浪和地震共同控制。因此，風-波浪對塔頂位移、結構泥面彎矩的影響顯著大于塔頂加速度。

(5) 從支撐結構安全角度看，弱震作用下，輪轂高度處平均風速取額定風速的風-波浪-地震作用組合為最不利地震荷載組合；強震作用下，最不利地震荷載組合為地震單獨作用。

本文根據風-波浪的統計關系，將風-波浪荷載作為整體，因此，風、波浪單因素的影響機制需進一步探討。同時，風-波浪-地震共同作用下，海上風機葉片變形較大，本文及現有研究尚未考慮幾何非線性的影響，后續工作將開展該問題的探討。