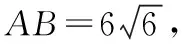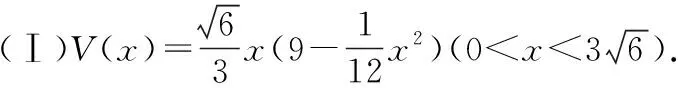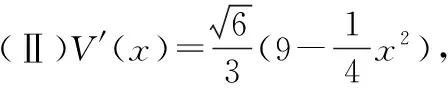淺談與導數應用問題交匯例題解析
甘肅 何偉軍
導數是研究函數性質和圖象的有力工具,導數除在求函數的單調性、曲線的切線、研究函數的圖象、求解函數極(最)值、判斷函數的零點和求參數的取值范圍等方面有著廣泛的應用外,“在知識的交匯處命題”的原則貫穿導數應用始終,由此也成為與其他各“知識塊”命題的生長點、交匯點和考查學生數學綜合能力的熱點.下文筆者將擷取與導數有關的試題進行分析,與大家分享.
一、集合知識與導數的交匯
集合是其他數學的基礎知識,把集合問題作為載體,求解不等式的解集為運算的核心,通過兩集合間的關系形成綜合問題是高考的重中之重.
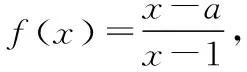
( )
A.(-∞,1) B.(0,1) C.(1,+∞) D.[1,+∞)
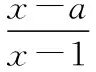
綜上可得MP時,a>1,故選C.
【評注】正確求出導函數,解有理分式不等式,理解集合的含義,再由MP,借助數軸列不等式或不等式組求其參數的取值范圍.注意運用分類討論與整合,數形結合思想方法,尤其需要注意端點值能否取到.
二、不等式與導數的交匯
函數、導數和不等式之間聯系非常緊密.不等式貫穿于函數的單調性、極值、最值和參數的取值范圍等問題中,這些都要通過函數“牽線搭橋”,用導數求解不等式問題,體現導數應用上的新穎性以及導數思想的重要性.
【例2】已知函數f(x)=ex+e-x,其中e是自然對數的底數.
(Ⅰ)證明:f(x)是R上的偶函數;
(Ⅱ)若關于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求實數m的取值范圍;
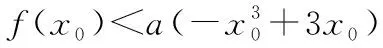
解析:(Ⅰ)證明略.
(Ⅱ)由mf(x)≤e-x+m-1得m(f(x)-1)≤e-x-1.
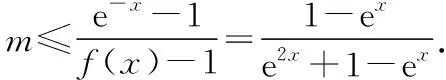
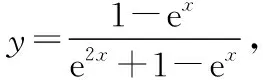
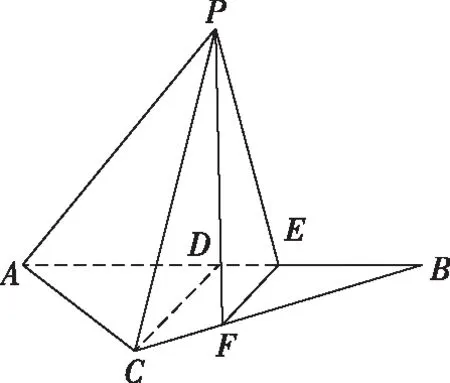
(Ⅲ)由題意,不等式f(x) 【評注】第(Ⅰ)問判斷偶函數;第(Ⅱ)問不等式恒成立問題;第(Ⅲ)問導數與函數的單調性,比較大小.解決含參數問題及不等式問題實現兩個轉化,一是利用導數解決含有參數的單調性問題可轉化為不等式恒成立問題,要注意化歸與轉化、分類討論和數形結合思想的應用.二是將不等式的證明、方程根的個數的判定轉化為函數的單調性、極值問題處理.無論何種問題,最終轉化為利用導數研究函數的單調性或最值,如何根據不等式的結構特征構造一個可導函數是證明不等式的關鍵. 我們知道數列是自變量取正整數時的函數,而導數又是研究函數性質的有力工具.因此,自然可聯想、嘗試應用導數知識解決數列的最大項或最小項問題;研究數列的增減性,證明數列不等式等. (Ⅰ)求數列{an}的通項公式; 又a1=2,a2+a4=8,所以a3=4,解得d=1,所以an=2+(n-1)·1=n+1. 三角函數與導數的交匯將是高考命題的一個新方向. ( ) A.(-∞,-6)∪(6,∞) B.(-∞,-4)∪(4,∞) C.(-∞,-2)∪(2,∞) D.(-∞,-1)∪(1,∞) 【評注】利用導數求三角函數的單調區間、最值、參數的取值范圍等,求解過程簡單,方法新穎別致,耳目一新.2013年全國卷Ⅱ理第16題、2014年遼寧卷理第21題、2015年陜西卷理第21題、2017年山東卷理第20題、2017年北京卷理第19題、2019年江蘇卷第20題第(2)問等,都是把求函數的導數、三角函數的有界性、解簡單的三角方程和一元二次不等式的解法緊密相連,起到多管齊下、一石二鳥的作用. 以平面向量為載體,利用向量的數量積、向量共線和模的概念可以把問題轉化為代數表達形式,脫去向量的外衣,轉化為代數問題,即運用導數方法解決有關問題. 導數的幾何意義把函數的導數與曲線的切線相聯系,使之成為知識交匯的一個重要載體.運用導數求圓錐曲線上任意一點的切線方程、直線與圓錐曲線關系中最值問題,當目標函數不能用一般方法求解時,轉化或換元為高次函數,可利用導數求出最值. (Ⅰ)求C的方程; (Ⅱ)P為C上的動點,l為C在P點處的切線,求O點到l距離的最小值. 【評注】第(Ⅰ)問可用平面向量的坐標運算,采用直接法求出點的軌跡;第(Ⅱ)問將曲線的切線與導數有機結合,考查點到直線的距離公式,基本不等式求最值的方法.問題設計精彩,知識面廣,基礎兼綜合. 將函數、導數和方程與概率統計問題綜合、整合與交匯,成為高考命題的創新點,如2018年全國卷Ⅰ理第20題,值得注意. 【例7】某工廠的某種產品成箱包裝,每箱200件,每一箱產品在交付用戶之前要對產品作檢驗,如檢驗出不合格品,則更換為合格品.檢驗時,先從這箱產品中任取20件作檢驗,再根據檢驗結果決定是否對余下的所有產品作檢驗.設每件產品為不合格品的概率都為p(0 (Ⅰ)記20件產品中恰有2件不合格品的概率為f(p),求f(p)的最大值點p0; (Ⅱ)現對一箱產品檢驗了20件,結果恰有2件不合格品,以(Ⅰ)中確定的p0作為p的值.已知每件產品的檢驗費用為2元,若有不合格品進入用戶手中,則工廠要對每件不合格品支付25元的賠償費用. (i)若不對該箱余下的產品作檢驗,這一箱產品的檢驗費用與賠償費用的和記為X,求EX; (ii)以檢驗費用與賠償費用和的期望值為決策依據,是否該對這箱余下的所有產品作檢驗? 所以EX=E(40+25Y)=40+25EY=40+25×18=490. (ii)由(i)可知一箱產品若全部檢驗只需花費400元,若余下的不檢驗則要490元,所以應該對余下的產品作檢驗. 【評注】本題以檢驗產品為命題背景,將概率統計知識與實際問題相結合,設計二項分布 “搭臺”、導數“唱戲”,數學期望“劇終”,體現了數學的應用價值與人文特色,給人以耳目一新感覺,但考生的閱讀理解能力以及應用數學知識解決實際問題的能力都不盡如人意,備考時應予以高度重視和反思. 曲線上的點列、遞推數列及導數知識交匯問題,它們均是在“知識網絡交匯點”命題,所涉及的知識點較多、內涵豐富.無論在知識方面還是在思維轉化方面都提出了較高要求,有較強的綜合性和一定的思維深度. (Ⅰ)求點Pn的坐標; (Ⅲ)設S={x|x=2xn,n∈N*},T={y|y=4yn,n∈N*},等差數列{an}的任一項an∈S∩T,其中a1是S∩T中的最大數,-265 又y′=2x+2n+3,當x=0時,kn=2n+3,所以 (Ⅲ)S={x|x=-(2n+3),n∈N,n≥1}, T={y|y=-(12n+5),n∈N,n≥1}={y|y=-2(6n+1)-3,n∈N,n≥1}, 所以S∩T=T,T中最大數a1=-17. 又an∈T,所以d=-12m(m∈N*)?d=-24,所以an=7-24n(n∈N*). 高考立體幾何與導數交匯的綜合題,以生活中的最優化問題(人教A版選修2-2P34)最為多見,主要是設置恰當的自變量,并確定自變量取值范圍,建立關于錐體、柱體體積的目標函數. 知識點的結合也比較精,以它的新穎性、綜合性而“閃亮登場”. (Ⅰ)求V(x)的表達式; (Ⅱ)當x為何值時,V(x)取得最大值? (Ⅲ)當V(x)取得最大值時,求異面直線AC與PF所成角的余弦值. 【評注】本題是簡單幾何體與導數的綜合題,解決本題的關鍵是建立四棱錐P-ACFE的體積V(x)與x的函數關系式,進而轉化為利用導數法求解V(x)的最大值問題,運算量不大,但沒有扎實的基本功和應對新題型的應變能力,就很容易導致解題錯誤甚至沒有解題思路. 通過以上各例的分析可以看出,導數之所以能作為壓軸題,必有其獨特的魅力,其魅力在于導數的聯系十分廣泛,因而在知識的交匯點處命題一直是高考的命題熱點.平時復習中有意識地將知識交匯的問題進行歸類、整理,了解知識交匯的一些特點,掌握新課標背景下依然堅持的高考命題的新視角,有利于獲得更大的效益.
三、數列與導數的交匯
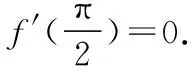
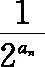
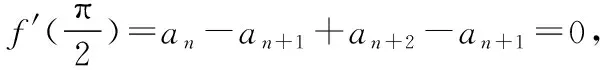
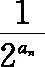
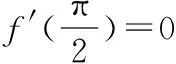
四、三角函數與導數的交匯
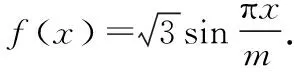
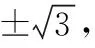
五、平面向量與導數的交匯
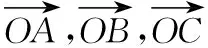
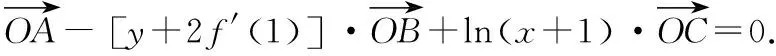
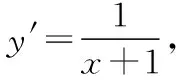
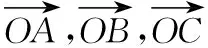
六、解析幾何與導數的交匯
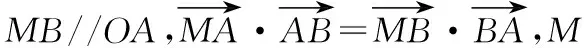
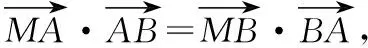
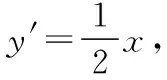
七、概率與導數的交匯
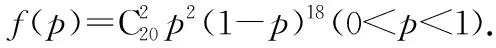
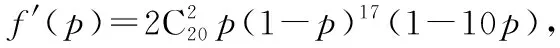
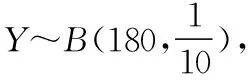
八、數列、解析幾何等與導數的交匯
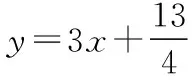
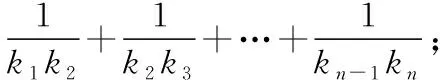
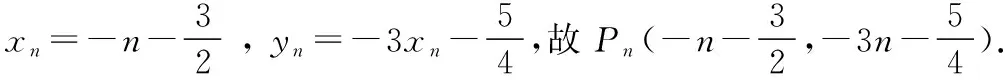
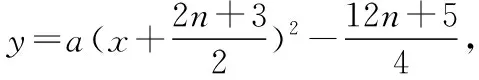
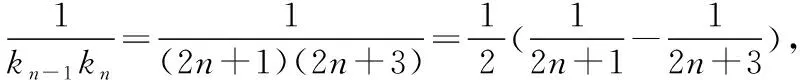
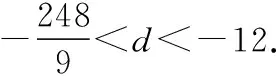
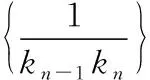
九、簡單幾何體與導數的交匯