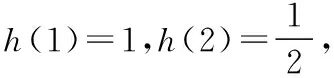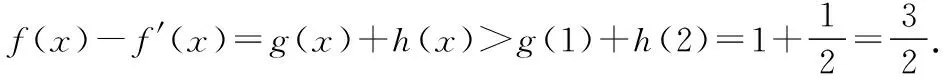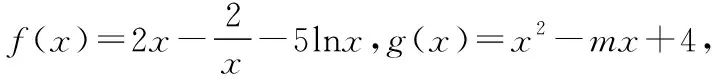不等式“恒成立”“存在成立”問題的破解策略

福建 吳志鵬 陳玉蘭

不等式“恒成立”與“存在成立”問題是高考熱點也是難點.它考查學生的化歸與轉化思想、邏輯推理和運算求解能力，要求學生具有扎實的數學基本功和較高的數學素養.不等式“恒成立”與“存在性”問題屬于“全稱量詞與存在量詞”的考查范疇，考綱要求并不復雜，但它涵蓋的知識量大，試題的難易度能得到比較好的控制.既可作為基礎題進行考查，有時也出現在選做題中；但它作為壓軸題考查時，常表現為一題中既有若干研究對象即若干函數(常見2個)，有若干變量，又有“存在”或“任意”等量詞的干擾，致使很大一部分的學生“望題生畏”，為了降低學生的解題難度，我們總結了以下破解策略.

一、排除干擾

弄清我們所要研究的對象，對于一些問題我們通過分離參數法、數形結合法、分類討論法等獲得以下兩個模型(包含了恒成立與存在成立)：

1.x∈D,m≥f(x)(m≤f(x))成立.

變式：①x∈D,m≥f(x)±g(x)(m≤f(x)±g(x))成立；

②x∈D,m≥f(x)·g(x)(m≤f(x)·g(x))成立；

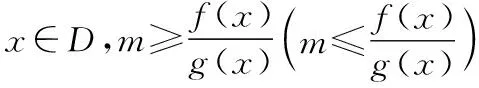
由于f(x),g(x)的變量是同一的，此時我們可將f(x),g(x)的關系式設為函數T(x)，這樣就能減少所需研究函數的個數，有助于提高解題效率.

2.x1∈A,x2∈B,f(x1)≤g(x2)成立或x1,x2∈A,f(x1)-f(x2)<0成立;

由于函數的自變量不同一，x1,x2可以相同也可以相異，為此我們必須分別研究函數f(x)與g(x)或是研究函數f(x)的最大值或最小值兩種情況.

研究對象的確定，主要是通過觀察函數自變量是否同一，同一則大多數情況可轉化為一個函數來研究，不同一則分成兩個函數進行研究或是研究一個函數的兩種情況.

二、轉化確立

1.文字語言的轉化，問題的呈現形式有：不等式的解集為R，不等式f(x)>0的解集為空集即f(x)≤0的解為全體實數；不等式在區間[a,b]上成立;不等式的解集包含[a,b]，以上幾種說法通常可轉化為不等式“恒成立”問題;不等式的解集不為空集；不等式有解;存在[a,b]，使得不等式成立等通常可轉化不等式“存在成立” 問題 .

2.對于不等式“恒成立”和“存在成立”這兩類問題，可轉化為求函數的最值比較問題，并利用其結果解決相應的求參問題或不等關系的證明.利用不等式“恒成立”解決“存在成立”問題，用熟悉的知識解決不熟悉的內容，是進行這類轉化的一種較好的方法.

①?x∈D,m≥f(x)(m≤f(x))成立?x∈D,m≥f(x)max(m≤f(x)min).

②?x∈D,m≥f(x)(m≤f(x))成立?x∈D,m≥f(x)min(m≤f(x)max).

學生對不等式“恒成立”問題比較熟悉，圖形意識也比較強烈，這類問題部分學生能夠很好地掌握，對比“恒成立”問題與“存在成立”問題，其實質只是對其最值的性質進行了變換，最大值與最小值的互換，這個特征也是不等式“恒成立”問題與“存在成立”問題最重要的區別，理解了其區別，轉化也就能做到“水到渠成”.

通過研究不等式恒成立問題：

?x1∈A,?x2∈B,f(x1)≤g(x2)成立

?f(x)max≤g(x)min,f(x)的定義域是A,g(x)的定義域是B.

通過不等式“恒成立”研究獲得“存在成立”問題的三個結論：

①?x1∈A,?x2∈B,f(x1)≤g(x2)成立

?f(x)max≤g(x)max,f(x)的定義域是A,g(x)的定義域是B.

②?x1∈A,?x2∈B,f(x1)≤g(x2)成立

?f(x)min≤g(x)min,f(x)的定義域是A,g(x)的定義域是B.

③?x1∈A,?x2∈B,f(x1)≤g(x2)成立

?f(x)min≤g(x)max,f(x)的定義域是A,g(x)的定義域是B.

三、函數研究

不等式“恒成立”“存在成立”問題轉化后就成了函數最值的比較，而要求函數的最值，就需要對函數進行研究，可利用導數、單調性的定義、基本不等式或函數的圖象等對其進行研究，以獲得函數在定義域內的最值.

四、結論獲取

通過比較函數的最值大小獲得參數的取值范圍或證明不等關系.

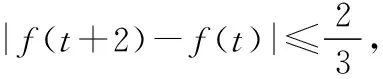
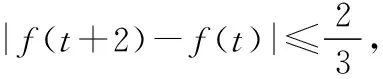
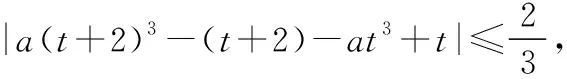
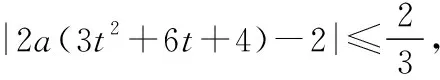
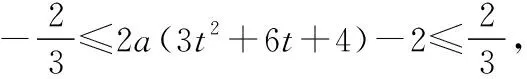
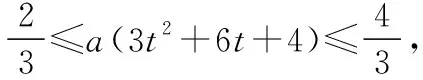
又3t2+6t+4=3(t+1)2+1≥1，

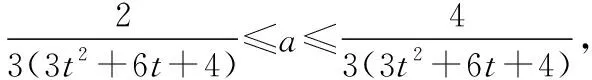
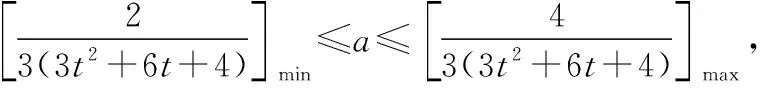
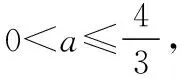
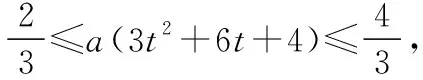
(Ⅰ)討論f(x)的單調性；

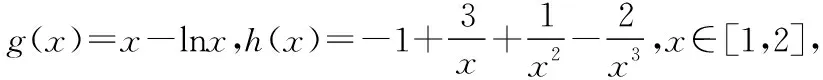
則f(x)-f′(x)=g(x)+h(x)，

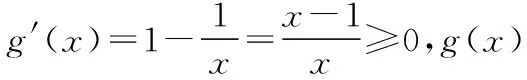
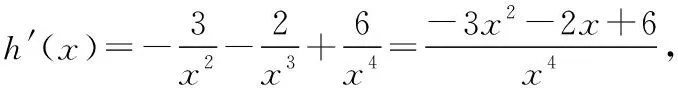
設φ(x)=-3x2-2x+6,則φ(x)在x∈[1,2]上單調遞減，因為φ(1)=1,φ(2)=-10,

所以存在x0∈(1,2)，使得φ(x0)=0，且

當10,h(x)單調遞增；

當x0

【例2】(2015·全國卷Ⅱ理·21)設函數f(x)=emx+x2-mx.

(Ⅰ)證明：f(x)在(-∞,0)上單調遞減，在(0,+∞)上單調遞增；

(Ⅱ)若對于任意x1,x2∈[-1,1]，都有|f(x1)-f(x2)|≤e-1，求m的取值范圍.

解：(Ⅰ) 證明：略

(Ⅱ)由(Ⅰ)知,f(x)在(-∞,0)單調遞減，在(0,+∞)單調遞增，即f(x)在[-1,0]單調遞減，在[0,1]單調遞增，

所以f(x)在x=0處取得最小值.

當m=0時,f(x)=1+x2，此時f(x)在[-1,1]上的最大值為2，最小值為1,

所以此時|f(x1)-f(x2)|≤2-1≤e-1成立.

當m≠0時，f(-1)=e-m+1+m,f(1)=em+1-m,

令g(m)=f(1)-f(-1)=em-e-m-2m，由g′(m)=em+e-m-2≥0,

得g(m)在R上單調遞增;

而g(0)=0，所以當m>0時，g(m)>0，即f(1)>f(-1),

所以當m<0時，g(m)<0，即f(1)

當m>0時，|f(x1)-f(x2)|≤f(1)-1=em-m≤e-1?0

當m<0時，|f(x1)-f(x2)|≤f(-1)-1=e-m+m≤e-1?-1≤m<0.

綜上所得m的取值范圍為[-1,1].

評析：本小題研究對象為函數f(x)，由于所給的自變量是不同一的，因此本題所研究的對象應視為函數f(x)的兩種最值情況；對于任意x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤e-1成立，可轉化為在區間[-1,1]上,|f(x1)-f(x2)|max≤e-1成立；研究函數f(x)在定義域內的最大值與最小值問題；最后利用不等關系進行比較獲得m的范圍.

g(x)在[1,2]上的最大值為max{g(1),g(2)}，所以有

解得m≥8-5ln2,

所以實數m的取值范圍為[8-5ln2,+∞).

評析：本題研究對象為不同的兩個函數f(x)和g(x)，且自變量也不是同一的，所以必須分別對兩個函數進行研究，利用不等式成立的類型進行轉化，即f(x)max≥g(x)max；在各自的定義域內利用導數或其他手段研究函數，尋求所需的最值；最后利用不等關系求得m的取值范圍.

結語：不等式“恒成立”“存在成立”問題的破解策略：排除干擾，通過自變量是否同一確定函數是否可合一，以減少函數個數的研究；再將不等式“恒成立”“存在成立”兩類不同情況轉化為求函數的某類最值問題，以“恒成立”為藍本進行“存在成立”的轉化；利用所學知識對函數的圖象或性質進行研究，以獲得所需的最值；比較最值獲得參數的范圍或證得結論.突破以上幾個關鍵的解題環節，破解不等式“恒成立”“存在成立”問題就將變得“輕而易舉”，其內容將不再是學生學習的難點.