一道省質檢試題多解探究與拓展
福建 陳凌燕 蔡海濤
每年全國各地的高三質檢卷,總有一些賞心悅目的試題,它們是命題老師智慧的結晶,對這些試題進行深入探究,挖掘試題背景及內涵,既能讓教學內容豐富多彩,又能激發學生的學習興趣,有利于拓展學生的思維,提升學生的素養,對高三的復習備考有很大的意義.下面筆者以2020年福建省高三畢業班質量檢查測試文科第20題為例進行說明.
一、試題呈現
(2020·福建省高三質檢文·20)已知拋物線C:y2=2px(0 (1)求C的方程; (2)是否存在垂直于x軸的直線l,使得l被圓M所截得的弦長為定值?若存在,求l的方程;若不存在,說明理由. 本題以拋物線為載體考查圓錐曲線的方程及其簡單幾何性質、圓的幾何性質等知識,考查推理論證能力、運算求解能力,考查數形結合思想、函數與方程思想,考查直觀想象、數學運算等核心素養,體現基礎性、綜合性.題目的特點是:(1)本題以拋物線與圓的組合型圓錐曲線為背景,需要觀察兩條曲線的特征,利用幾何圖形的性質解題,體現考查的綜合性;(2)本題求解的問題為曲線的軌跡方程及定值問題,這兩個問題均是解析幾何中重要的問題,也是近年高考中的高頻考點,體現模擬考試與高考接軌的功能;(3)本題第二問有多種解法,不同解法思路體現考生思維的差異性;(4)第二問是探索性問題,具有開放性和發散性,此類問題的條件和結論不完備,需要結合已知條件或假設新的條件進行探究、觀察、分析、抽象、概括等,是素養導向下的典型題型. 本題(1)問易得C:y2=4x.(解答過程略) (2)問是探索直線存在性問題,求解這類問題常有兩個思路. 思路一:“肯定順推法”,即將不確定性問題明朗化.其步驟為:假設滿足條件的元素(點、直線、曲線或參數)存在,用待定系數法設出,列出關于待定系數的方程組,若方程組有實數解,則元素存在;否則,元素不存在. 思路二:利用特殊與一般思想,先猜想后證明. 解法綜述:假設滿足題意的直線l:x=a存在,在A的運動過程中取兩個特殊位置,比如當A運動到A(0,0)和A(4,4)時,求圓M的圓心坐標與半徑,進一步利用垂徑定理分別求出兩個特殊圓截l的弦長,因為弦長為定值,建立方程求得a=3,即表明“若l存在,則只可能為x=3”,再證明圓M截l的弦長為定值,便可證明l為符合題意的直線,從而解決問題. 1.引申推廣 解完此題,筆者意猶未盡,對問題加以推廣探究,得到如下兩個問題. 探究一:已知A是拋物線C:y2=2px(p>0)上一動點,點Q(q,0).是否存在垂直于x軸的直線l,使得l被以線段QA為直徑的動圓M所截得的弦長為定值?若存在,求l的方程;若不存在,說明理由. 設l被以線段QA為直徑的動圓M所截得的弦長為t, 探究二:已知A是拋物線C:y2=2px(p>0)上一動點,定直線l:x=a,是否存在x軸上的定點Q,使得l被以線段QA為直徑的動圓M所截得的弦長為定值?若存在,求定點Q的坐標;若不存在,說明理由. 設l被以線段QA為直徑的動圓M所截得的弦長為t, 此時t2=2ap>0,即a>0, 當a≤0時,不存在; 特別地,當a=0時,直線l即y軸,取點Q為拋物線焦點,此時動圓與y軸相切. 2.類比探究 基于以上的引申推廣,類比橢圓與雙曲線是否也具有類似的性質. 設l被以線段QA為直徑的動圓M所截得的弦長為t, 所以不存在直線滿足題意. 雙曲線與橢圓類似,不存在符合條件的直線,結論也不成立. 我們解題時常有“似曾相識燕歸來”的感覺,這就是類比.教師要引導學生由一個數學對象的性質遷移到另一個數學對象上去,從而獲得另一個對象的性質,這是解決數學問題的常用方法,當然由此例還可看出類比僅僅是種猜測,結論未必正確,需要進行驗證. 3.變式拓展 (1)已知A是拋物線C:y2=4x上一動點,點Q(2,0),垂直于x軸的直線l被以線段QA為直徑的動圓M所截得的弦長為定值,則Q到直線l的距離為________. (i)求E的方程; (ii)過點F的直線交E于A,B兩點,以AB為直徑的圓D與平行于y軸的直線相切于點M,線段DM交E于點N,證明:△AMB的面積是△AMN面積的四倍. 解:(i)化簡得E的方程為y2=4x(x>0).(過程略) 依題意可設直線AB的方程y=k(x-1)(k≠0), 故S△AMB=4S△AMN. 羅增儒教授說過:數學解題的四個水平為:模仿、練習、領悟、理解.教師設計變式練習,是提升學生解題能力的有效途徑.二、試題特點
三、解法探析

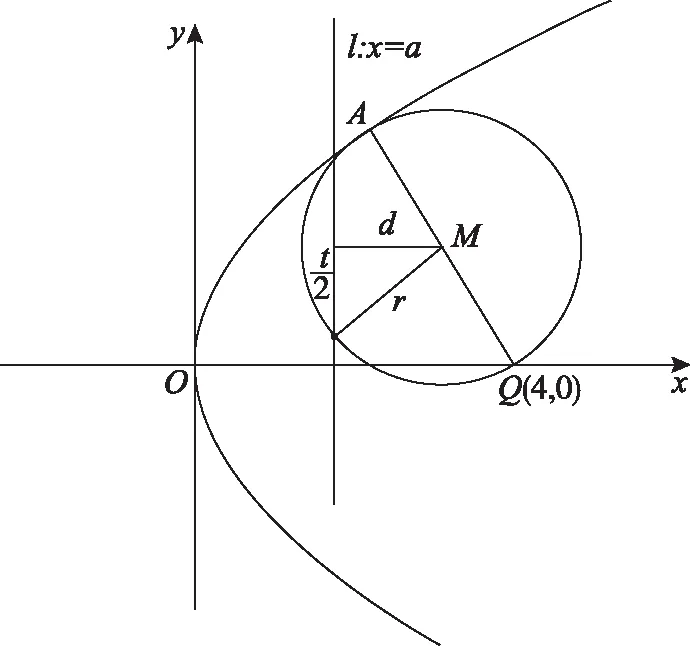
四、試題反思
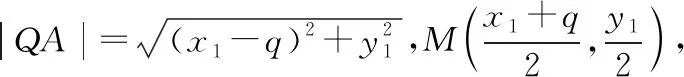
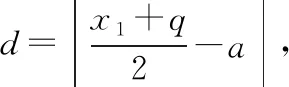





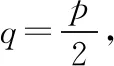
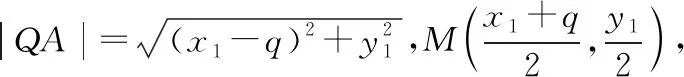
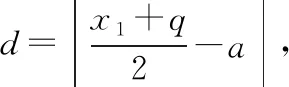



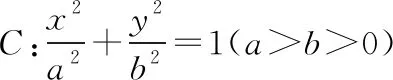
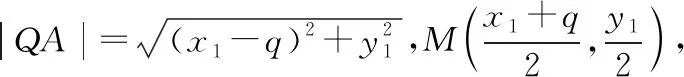
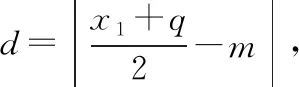
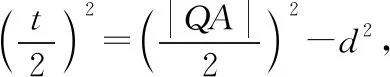
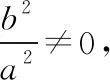


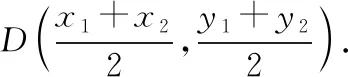
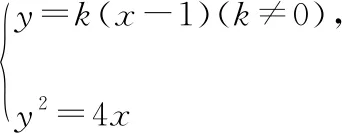
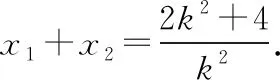
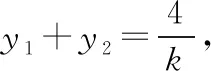
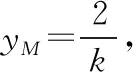
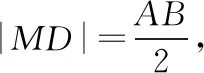

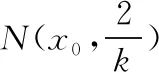


五、結語


