12 Bit量化誤差對正弦參數擬合影響的誤差界

梁志國

（航空工業北京長城計量測試技術研究所 計量與校準技術重點實驗室，北京100095）

0 引言

四參數正弦曲線擬合在計量測試領域應用廣泛，它可以獲得擬合正弦波形的幅度、頻率、相位、直流分量四個參數，還可以用于A/D有效位數的評價［1-11］。有關這些參數的擬合誤差，一直受到關注［12-17］，但卻缺乏簡便易行的獲取方法。

相關研究中，以美國NIST的Deyst等人的最為著名［18］，研究內容主要涉及影響誤差的因素包括諧波、抖動、信噪比、初始相位、序列（周波數、序列長度）等，這些因素對幅度、頻率、初始相位、直流分量四個擬合參數的影響，分別通過經驗公式和仿真曲線的方式予以表征，給出了這些因素產生影響的誤差界。后續的以正弦模型為基礎的擬合參數的不確定度評定，多以此研究工作為基礎［19-21］。該項工作需要先對正弦采樣序列分別進行諧波分析、抖動分析和噪聲分析，然后確定誤差界。關于抖動分析，除文獻［22］以外，未發現有其它理想的方式可進行全部四個參量的抖動分析。另外，由于采樣序列均有量化誤差存在，量化誤差對擬合參數的影響并未單獨提及。

與眾多誤差因素相比，量化誤差是起決定因素的主導分量。此時，其對正弦序列擬合參數誤差的影響狀況如何也是人們最為關注的，并不是簡單套用上述Deyst等人的工作結論就能圓滿解決的。

在工程實踐中，12位A/D的數據采集系統應用最為廣泛，本文將以12位A/D的量化為前提條件，通過仿真搜索，分別變化幅度、頻率、初始相位、直流分量、序列所含周波數、序列長度等測量條件，尋找出擬合正弦參數變化的誤差界，以便給12位A/D的采集測量場合四參數正弦擬合的誤差和不確定度評定提供參考和借鑒。并在已有測量誤差要求的前提下，通過選擇測量條件達到測量目的。

2 基本思想

2.1 測量條件

在正弦波數據采集中，被測波形的幅度、頻率、直流分量等參量，包括抖動、失真、諧波、噪聲等參量，是客觀存在的，很難被干預而變動。而測量條件，包括測量儀器系統的幅度量程、A/D位數、采樣速率、存儲深度、通頻帶、幅度測量誤差、線性度、采樣速率誤差等，則可通過自主選擇而變化。

在正弦波采樣測量中，采樣速率與信號頻率之比是每個周波的采樣點數，可通過選擇采樣速率改變比值；當其確定后，采樣序列長度決定了其所包含周波數的多少。

通過選取量程，改變被測信號幅度與量程的占比；通過選擇不同A/D位數的測量儀器和系統，改變量化誤差的大小。最終，用于改變正弦波擬合參數的誤差界。

綜合考慮各方面因素，選出具有相互獨立性和系統完備性的左右量化誤差影響的測量條件包括：

①A/D位數：用于確定量化水平及影響；②采樣序列包含周波數：確定周波數的影響；③序列樣本點數：確定存儲深度的影響；④信號幅度：確定幅度變動的影響；⑤初始相位：確定信號相位變化帶來的影響；⑥直流分量：確定直流分量變化帶來的影響。

經過四參數正弦曲線擬合后，獲得的指標特征參量包括：①有效位數誤差界，以Bit表述；②擬合幅度誤差界，以LSB表述；③擬合頻率誤差界，以相對誤差表述；④擬合相位誤差界，以度（°）表述；⑤擬合直流分量誤差界，以LSB表述。其中，LSB（least Bit）稱為最小量化階梯值，有時也稱為量化誤差值，由采集系統的量程和采用的A/D位數確定。

2.2 誤差界搜索

正弦參數擬合的誤差界，是在上述六項測量條件下，固定其中的五項，變化一項，搜索出該條件變化時，四參數正弦擬合所獲得的有效位數、幅度、頻率、相位、直流分量等五項指標的誤差界。

3 仿真實驗及數據處理

3.1 仿真實驗條件

為方便參數調控，不失一般性，設定包含六項測量條件的仿真實驗條件包括：

1）A/D位數

A/D位數的基本參量為12 bit。

2）采樣序列包含周波數

未特別說明時，采樣序列包含周波數為20個；作為主變化因素時，變化范圍為0.90～21.00個周波，0.01周波步進；作為輔助變化量時，變化范圍為2～20個周波，1周波步進。

3）序列樣本點數

未特別說明時，序列樣本點數為16000點；作為主變化因素時，變化范圍為100～16000點，1點步進；作為輔助變化量時，變化范圍為1000～16000點，1000點步進。

4）信號幅度

未特別說明時，幅度為（85.4494%×量程）；作為主變化因素時，幅度宏觀變化范圍為量程的4.883%～100%，0.1 LSB步進；作為輔助變化量時，在（85.4494%×量程點）處，其微觀變化范圍為-0.5 LSB～0.5 LSB，0.1 LSB步進。

5）初始相位

未特別說明時，初始相位為0°；作為主變化因素時，變化范圍為-180°～180°，0.1°步進；作為輔助變化量時，變化范圍為-180°～180°，20°步進。

6）直流分量

未特別說明時，直流分量為0；作為主變化因素時，變化范圍為-2 LSB～2 LSB，0.01LSB步進；作為輔助變化量時，變化范圍為-0.5 LSB～0.5 LSB，0.1 LSB步進。

3.2 仿真實驗結果

按照上述仿真實驗條件，分別以一種參量為主變化因素、另一種參量為輔助變化因素生成實際的仿真條件，考察各指標要素的誤差變化情況。

3.2.1 幅度作為主變化因素

當幅度作為主變化因素時，周波數作為輔助變化量，獲得如圖1所述的誤差變化曲線波形；相位作為輔助變化量，獲得如圖2所述的誤差變化曲線波形；直流分量作為輔助變化量，獲得如圖3所述的誤差變化曲線波形；數據點數作為輔助變化量，獲得如圖4所述的誤差變化曲線波形。

3.2.2 周波數作為主變化因素

當周波數作為主變化因素時，幅度作為輔助變化量，獲得如圖5所述的誤差變化曲線波形；初始相位作為輔助變化量，獲得如圖6所述的誤差變化曲線波形；直流分量作為輔助變化量，獲得如圖7所述的誤差變化曲線波形；數據點數作為輔助變化量，獲得如圖8所述的誤差變化曲線波形。

圖1 幅度與周波數同時變化時的參數擬合誤差界

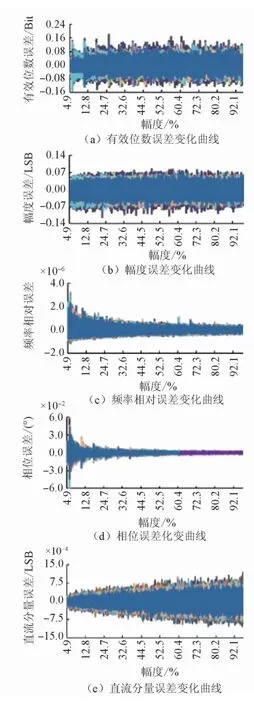
圖2 幅度與相位同時變化時的參數擬合誤差界

圖3 幅度與直流分量同時變化時的參數擬合誤差界

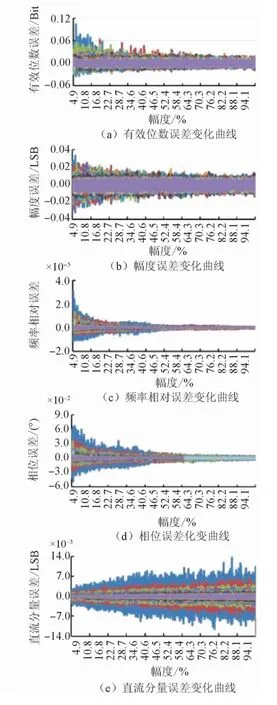
圖4 幅度與數據點數同時變化時的參數擬合誤差界

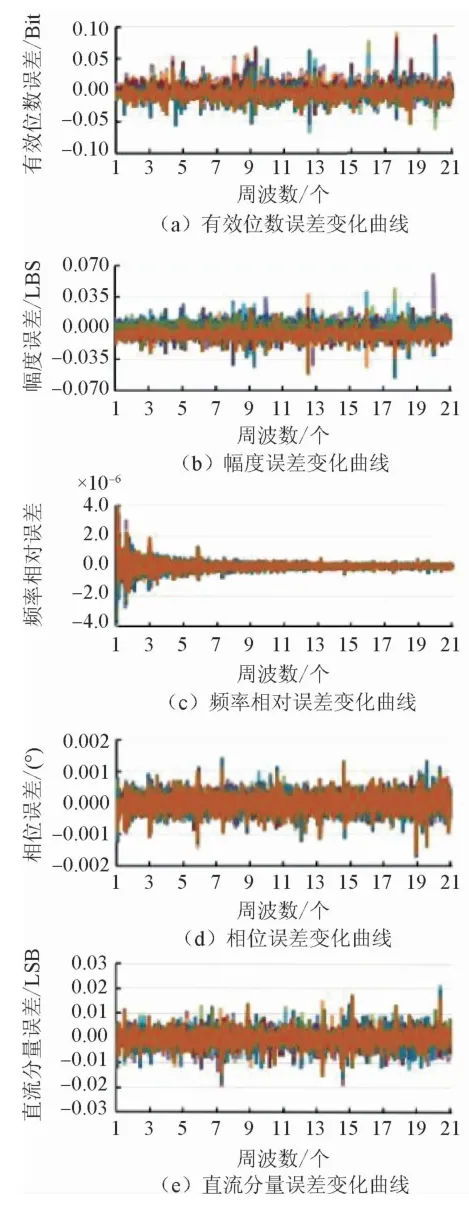
圖5 周波數與幅度同時變化時的參數擬合誤差界

圖6 周波數與相位同時變化時的參數擬合誤差界

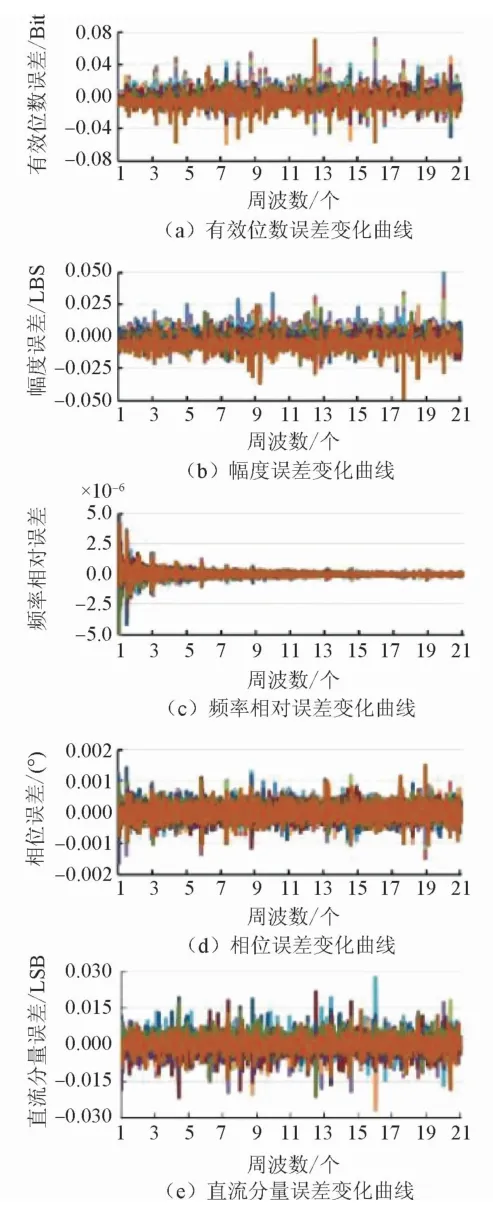
圖7 周波數與直流分量變化時的參數擬合誤差界

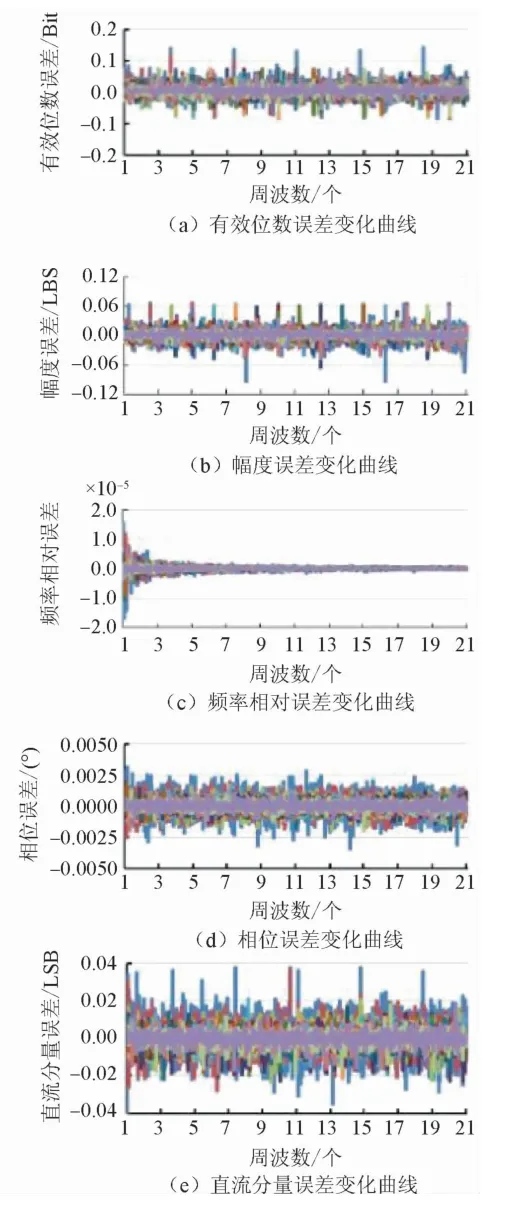
圖8 周波數與數據點數變化時的參數擬合誤差界

3.2.3 初始相位作為主變化因素

以初始相位作為主變化因素時，幅度作為輔助變化量，獲得如圖9所述的誤差變化曲線波形；周波數作為輔助變化量，獲得如圖10所述的誤差變化曲線波形；直流分量作為輔助變化量，獲得如圖11所述的誤差變化曲線波形；數據點數作為輔助變化量，獲得如圖12所述的誤差變化曲線波形。

3.2.4 直流分量作為主變化因素

以直流分量作為主變化因素時，幅度作為輔助變化量，獲得如圖13所述的誤差變化曲線波形；周波數作為輔助變化量，獲得如圖14所述的誤差變化曲線波形；初始相位幅度作為輔助變化量，獲得如圖15所述的誤差變化曲線波形；數據點數作為輔助變化量，獲得如圖16所述的誤差變化曲線波形。

3.2.5 數據點數作為主變化因素

以數據點數作為主變化因素時，幅度作為輔助變化量，獲得如圖17所述的誤差變化曲線波形；周波數作為輔助變化量，獲得如圖18所述的誤差變化曲線波形；初始相位作為輔助變化量，獲得如圖19所述的誤差變化曲線波形；直流分量作為輔助變化量，獲得如圖20所述的誤差變化曲線波形。

3.3 仿真實驗結果分析

3.3.1 有效位數誤差界

從圖1（a）～圖20（a）可以看出：

1）數據點數是影響有效位數誤差界（誤差包絡線）的最重要因素，總體而言，當數據點在1000點以下時，隨著數據點數的增大，可導致有效位數誤差界的單調變窄。當數據點在1000點以上時，誤差帶比較平穩，此時，有效位數誤差界下界為-0.2 Bit，上界為0.5 Bit。

2）當幅度在量程范圍內大尺度變化時，在半量程以下，且數據點數較少時（例如幾千點以下），有效位數誤差界隨幅度增加呈緩慢下降趨勢；當幅度量程比在50%以上時，誤差界趨于平穩，其誤差下界為-0.21 Bit，上界為0.25 Bit；若數據點數達到9000點以上，可以導致其誤差下界為-0.2 Bit，上界為0.2 Bit。幅度在LSB量值尺度的微觀進行變化時，有效位數誤差隨幅度變化呈局部周期性變化，幅度周期為1 LSB。

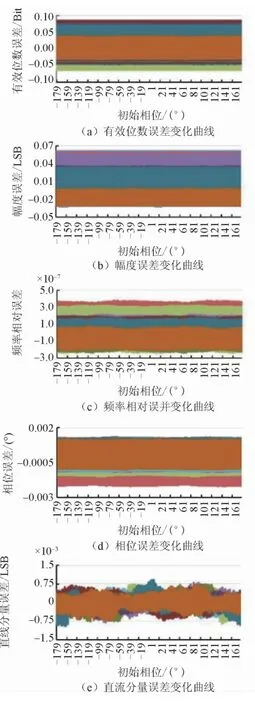
圖9 初始相位與幅度同時變化時的參數擬合誤差界

圖10 初始相位與周波數變化時的參數擬合誤差界

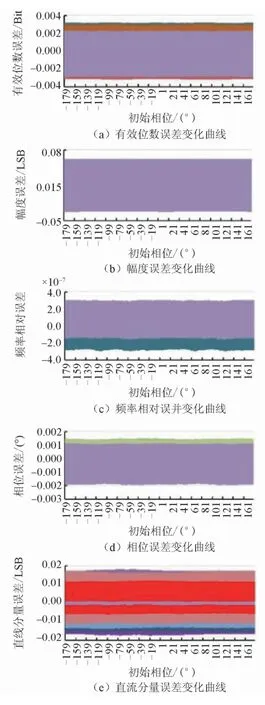
圖11 初始相位與直流分量變化時的參數擬合誤差界

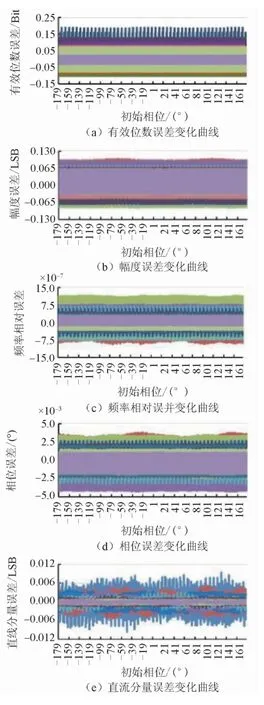
圖12 初始相位與數據點數變化時的參數擬合誤差界

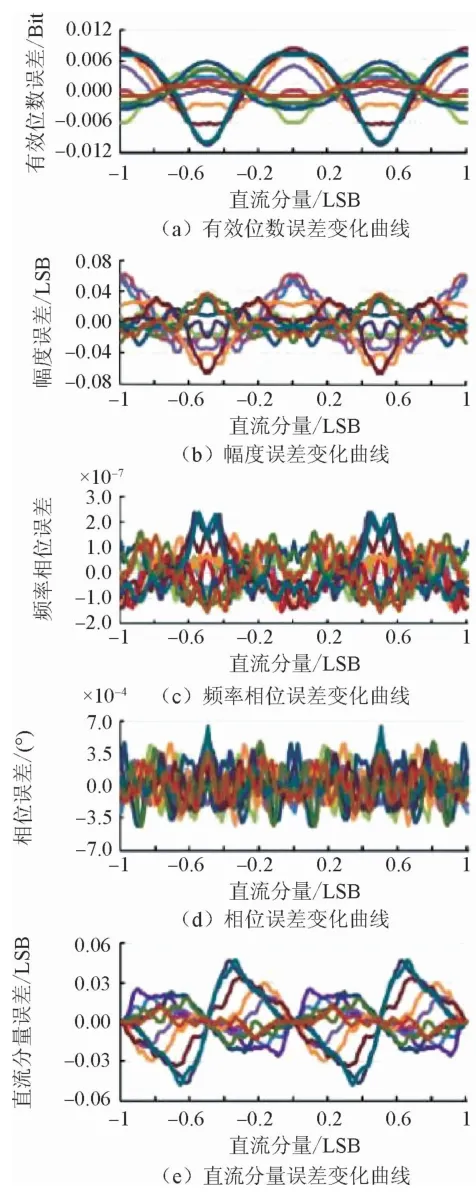
圖13 直流分量與幅度變化時的參數擬合誤差界

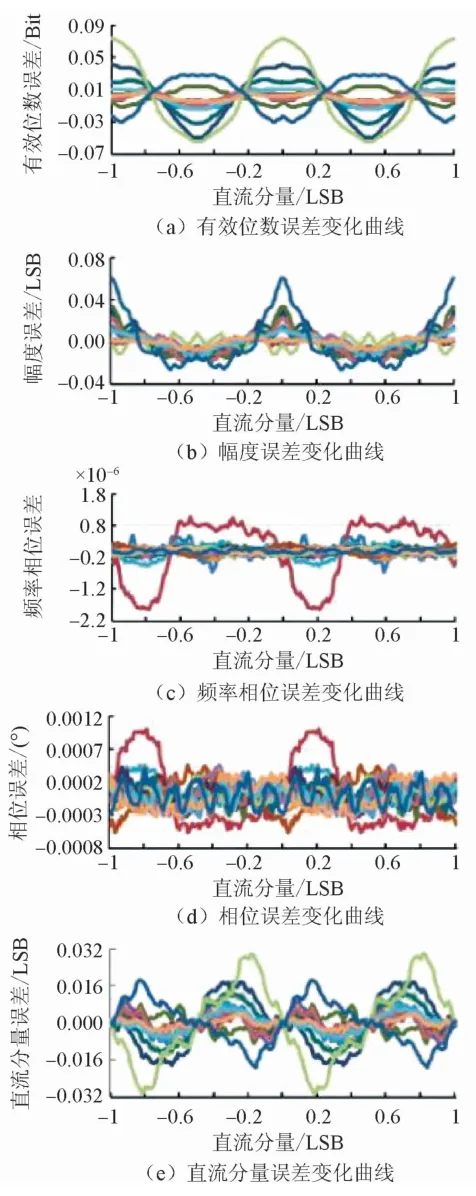
圖14 直流分量與周波數變化時的參數擬合誤差界

圖15 直流分量與相位變化時的參數擬合誤差界

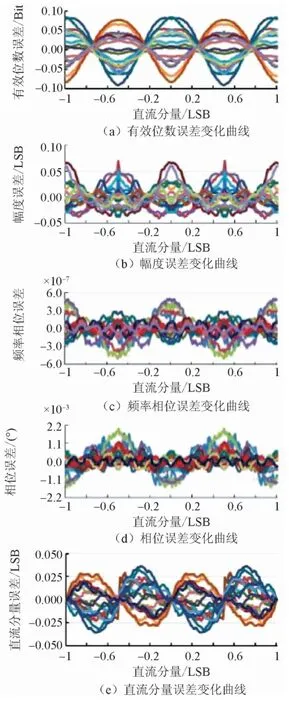
圖16 直流分量與數據點數變化時的參數擬合誤差界

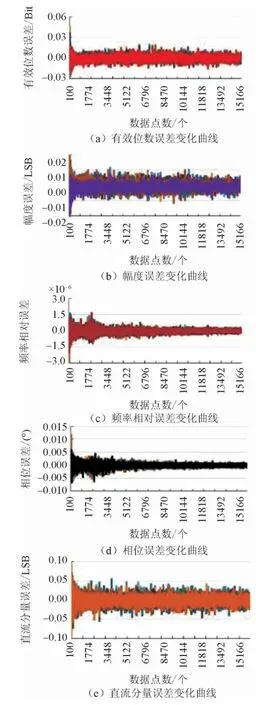
圖17 數據點數與幅度變化時的參數擬合誤差界

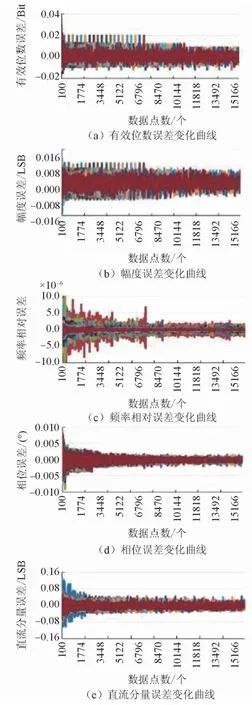
圖18 數據點數與周波變化時的參數擬合誤差界

圖19 數據點數與相位變化時的參數擬合誤差界

圖20 數據點數與直流分量變化時的參數擬合誤差界

3）有效位數誤差不隨周波數的變化而變化的趨勢，其誤差帶平穩，且存在個別跳動點，誤差帶下界為-0.08 Bit，上界為0.08 Bit。

4）初始相位因素對有效位數影響的誤差帶波動平穩，但是，幅度、周波數、直流分量等因素會影響誤差帶寬度和位置，其波動的誤差下界為-0.1 Bit，上界為0.2Bit。

5）直流分量在LSB量值尺度進行微觀變化時，有效位數誤差隨其變化呈周期性變化，幅度周期為1 LSB，其波動的誤差下界為-0.1 Bit，上界為0.085 Bit。在直流分量變化時，其它因素的變化對誤差界也有影響，按照影響由大到小，依次為幅度、數據個數、周波數、初始相位。

3.3.2 幅度誤差界

從圖1（b）～圖20（b）可以看出：

1）數據點數是影響幅度誤差界的重要因素，當數據點在1000點以下時，隨著數據點數的增大，可導致幅度誤差界的單調變窄；當數據點在1000點以上時，其誤差界趨于平穩，此時，誤差界下界約為-0.1 LSB，上界約為0.1 LSB。

2）在量程范圍內大尺度變化時，幅度誤差界隨幅度增加呈平穩趨勢，下界均為-0.2 LSB，上界為0.2 LSB，其它對其影響的因素按重要性排列依次為數據個數、直流分量、初始相位、周波數。幅度在LSB量值尺度的微觀進行變化時，幅度誤差隨幅度變化呈局部周期性變化，下界為-0.07 LSB，上界為0.06 LSB，變化周期為1 LSB，不同幅度將改變幅度誤差的量值。

3）周波變化給幅度誤差界帶來的影響比較平穩，下界約為-0.06 LSB，上界約為0.06 LSB，但不同的周波的誤差界差異可能較大。

4）初始相位因素的影響處于平穩波動狀態，不同初始相位的波動帶可能有明顯的寬窄和位置差異，下界為-0.08 LSB，上界為0.09 LSB。

5）幅度誤差界隨直流分量的變化呈周期變化，周期為1 LSB，下界為-0.07 LSB，上界為0.06 LSB。

3.3.3 頻率誤差界

從圖1（c）～圖20（c）可以看出：

1）數據點數與周波數的結合是影響頻率誤差界的最重要因素。數據點數的增大，可以導致頻率誤差界的變窄，但并非單調變窄。1000點以上的數據點數，1/4量程以上的幅度，可以獲得頻率誤差界下界為-1.0×10-5，上界為1.0×10-5；更窄的誤差界需要更多的數據點數。

2）頻率誤差隨幅度增加呈衰減下降趨勢，但不是單調下降，主要由幅度、周波數的變化確定，半量程幅度以后，其頻率誤差下界為-1.8×10-6，上界為2.6×10-6。

3）周波數增大時，頻率誤差隨周波數增加呈震蕩衰減趨勢，但并不一直單調下降，其中，與初始相位結合的影響比其它因素顯著，4個周波以上時，頻率誤差下界為-1.5×10-5，上界為1.5×10-5。

4）初始相位、直流分量因素的影響可以忽略。

3.3.4 初始相位誤差界

從圖1（d）～圖20（d）可以看出：

1）數據點數與周波數的結合，是影響初始相位誤差界的最重要因素，數據點數的增大，可以導致初始相位誤差界的變窄，但并非單調變窄。1000點以上的數據點數，其誤差界下界為-0.06°，上界為0.06°；更窄的誤差界需要更多的數據點數。

2）初始相位誤差隨幅度增加呈衰減下降趨勢，但不單調下降，主要由幅度、周波數的變化確定，下界為-0.018°，上界為0.014°；半量程以上的幅度，可以降為下界為-0.001°，上界為0.001°。

3）當周波數變化時，初始相位誤差界比較平穩，下界為-0.001°，上界為0.001°；在數據個數較低時，會有較大跳變，下界為-0.0025°，上界為0.0025°。

4）初始相位誤差界，隨初始相位本身、直流分量等各種因素影響而變化的規律均為平穩。下界為-0.002°，上界為0.002°；當數據個數較少時，會有增加，可達下界為-0.005°，上界為0.005°。

3.3.5 直流分量誤差界

從圖1（e）～圖20（e）可以看出：

1）數據點數是影響直流分量誤差界的重要因素之一，在1000點以下，數據點數的增大，可以導致直流分量誤差界的變窄；1000點以上，其誤差界比較平穩，下界為-0.05 LSB，上界為0.05 LSB。

2）0值的直流分量誤差界隨幅度增加呈緩慢上升趨勢，主要由于幅度上升后，接近0值的直流分量與其相差懸殊，運算舍入誤差造成，下界為-0.014 LSB，上界為0.014 LSB；非0值的直流分量誤差界量值由幅度、直流分量組合變化確定，幅度大尺度變化時，誤差界比較平穩，下界為-0.08 LSB，上界為0.08 LSB；隨著直流分量的不同，誤差界寬度與位置呈較多的變化。

3）周波數為2及以上時，同一周波數，直流分量誤差界隨幅度增加呈緩慢增加規律性變化；而不同周波數時，直流分量誤差界有顯著不同，并無單調趨勢；當周波數為1時，幅度直流分量誤差界有顯著性增大，且誤差界變化的規律為隨幅度增加呈緩慢下降趨勢。

4）初始相位因素對直流分量誤差的影響可以忽略，下界為-0.005 LSB，上界為0.005 LSB。

5）直流分量在LSB尺度的微觀變化將導致其自身誤差較大變化，局部具有周期性特征，以1 LSB為周期，下界為-0.02 LSB，上界為0.02 LSB。

表1 正弦擬合參數的條件誤差界（12Bit A/D）

4 問題討論

上述過程，是提取出幅度、周波數、相位、直流分量和數據點數作為變動參量，使用有效位數誤差、幅度誤差、頻率相對誤差、相位誤差和直流分量誤差作為正弦擬合結果的指標參量。并以其中每一參量作為主變動因素，其它四項參量作為輔助變量的情況進行了二維搜索，揭示了雙變量組合變化情況下的各個指標參量誤差界的變化情況，獲得了不同組合實驗條件下的誤差界測量曲線。結果表明：

1）擬合序列的數據點數仍然是最重要的測量條件，也是影響擬合結果的誤差界的主導條件，若想獲得更高準確度的擬合結果，通常需要更多的數據點數。就本文所述的有20個周波的測量序列而言，8000點以上的數據點數可以獲得更良好的擬合結果。

對于隨機噪聲的影響而言，擬合序列的數據點數的增加，可以導致擬合結果誤差界的單調下降，而本文的實驗表明，對于量化誤差的影響而言，并未完全呈現出同樣的單調規律，具體原因需要將來進一步研究予以解決。

2）波形幅度是指其相對量程范圍的占比而言，實驗表明，相對于相鄰幅度，擬合頻率誤差和擬合相位誤差均較大，并且這樣的幅度規則出現，原因不明，需要進一步研究予以解決。超過半量程以后幅度的信號波形，其擬合誤差界趨于平穩。因此，測量活動應盡量選擇半量程以上覆蓋率的幅值進行。

3）周波數的影響實際上體現的是采樣速率和信號頻率比的影響，實驗表明，只有頻率擬合誤差隨周波數的增加呈震蕩衰減趨勢，并且周波數越小，變化趨勢越顯著，在10個周波以后的變化趨勢趨于平穩。某些周波點上，誤差界會有突然增大的現象，具體原因需要進一步研究。

若想獲得較小的擬合誤差，則應適當提高擬合序列周波數，至少應為2個周波以上；和多周波條件相比，2個以下的周波數將使得擬合誤差顯著升高。

對于頻率以外的其它參數，非整數的周波數變化，會給誤差界帶來小幅波動；但誤差帶的總體趨勢平穩，隨周波數變動沒有明顯趨勢性變化。

4）初始相位的變化，對每一個參量擬合的影響都處于變化狀況，當其它因素固定時，僅由初始相位變化導致的各個參數誤差帶波動平穩。但其它因素變化后，由初始相位變化導致的各個參數誤差帶寬度和位置可以有較大變化。

其對于有效位數誤差帶的影響約為±0.1 Bit；對于幅度擬合誤差帶的影響約為±0.1 LSB；對于頻率擬合誤差帶的影響約為±1.0×10-6；對于初始相位擬合誤差帶的影響約為±0.0042°；對于直流分量擬合誤差帶的影響約為±0.01 LSB。

5）直流分量的變化，本文只關注到了LSB量值范圍的變化帶來的影響，在該尺度上，它的變化給每一個參量的誤差帶均帶來周期性影響，給其它參量誤差帶的影響均呈現明顯的對稱性，而給直流分量自己的誤差帶的影響則具有反稱性特征。

配合其它因素的變動，直流分量的微觀變化可對有效位數造成的誤差帶的影響約為±0.1 Bit；對于幅度擬合誤差帶的影響約為±0.1 LSB；對于頻率擬合誤差帶的影響約為±5.0×10-7；對于初始相位擬合誤差帶的影響約為±0.002°；對于直流分量擬合誤差帶的影響約為±0.05 LSB。

6）若在實際工作中，并不需要獲得全部上述5個參量，而僅僅需要其中某一個參量的高精度結果，例如有效位數，則可以根據該參量的影響因素顯著程度，只注意調控和構建所需要的影響量條件即可，其它可以自由選取，不必全盤考慮，將使得實驗設計更加容易些。

通過和4 Bit及8 Bit A/D量化的仿真數據相比，12 Bit量化的誤差界有著很多不同的特征。其中，最大特征是幅度變化和直流分量變化對誤差界的影響占比變弱，而初始相位變化對誤差界影響的占比增強，并且，誤差界的變化趨勢更趨平穩，誤差界的量值也有很大差異，尚無普適性規律，很難使用一個代替另外一個，需要分別搜索和應用。

5 結論

文章通過大量仿真實驗，對使用12 Bit A/D轉換器的測量系統所得的正弦測量序列，在波形擬合中獲得的幅度、頻率、初始相位、直流分量和有效位數5個參數的擬合誤差界進行了搜索研究，給出了誤差界隨波形幅度、周波數、初始相位、直流分量、數據點數等不同組合條件而變化的曲線，揭示出其變化規律。

例如，頻率擬合誤差界隨幅度宏觀上升變化而呈現出的總體下降趨勢；隨幅度和直流分量在LSB尺度的微觀變化呈現出的周期性變化規律；隨周波數、數據點數上升而呈現出的總體下降趨勢；并發現了誤差規律隨幅度、周波數、數據點數上升過程中的非單調現象；總結出了顯著影響量和非顯著影響量。對正弦擬合參量的不確定度評估和誤差界定具有重要意義和價值。另外，對于擬合參數誤差有明確要求的場合，可以通過構筑相適應的測量條件獲得預期結果。由于使用12 Bit A/D轉換器的數據采集系統眾多，正弦擬合越來越成為高精度測量分析的重要手段，因而，本文獲得的結論將擁有良好的實際應用前景。