基于教材的小學數學拓展課程設計原則

童義清

摘? ? 要?? ?小學數學拓展課程，是基礎課程的有益補充，是發展小學生數學核心素養的重要載體。基于教材設計小學數學拓展課程，須保證課程設計基于真實學情，目標清晰明確;確保基礎課程到拓展課程的過渡由易到難，且拓展課程本身也應由簡單到復雜;兼顧拓展課程內容的典型性和解決問題策略的典型性，幫助小學生“見‘少識‘廣”;提升拓展課程的吸引力，達到“有意義且有意思”。

關鍵詞? ?教材 小學數學 拓展課程 設計原則

小學數學拓展課程，作為基礎課程的有益補充，它是兒童進一步探索新知識的材料、進一步提升核心素養的載體，更是進一步感悟數學魅力的平臺。然而就普通小學數學教師而言，限于課程研發理論、研發經驗和實施條件的束縛，“基于教材—因需設計—班本實施”，不失為一種靈活實用的拓展方式。下面，筆者就從教材的角度談談小學數學拓展課程設計的基本原則。為了方便交流，以蘇教版《數學》六年級下冊“圓柱的表面積”為例，分享筆者設計的“多變的圓柱表面積”這一拓展課。

一、目的性

有的放矢，是研發和設計拓展課程的基本原則。為什么要設計“多變的圓柱表面積”這節拓展課呢？這是因為筆者發現：對六年級的學生而言，“圓柱的表面積”這一課學生學得既“不過癮”，也“不徹底”。

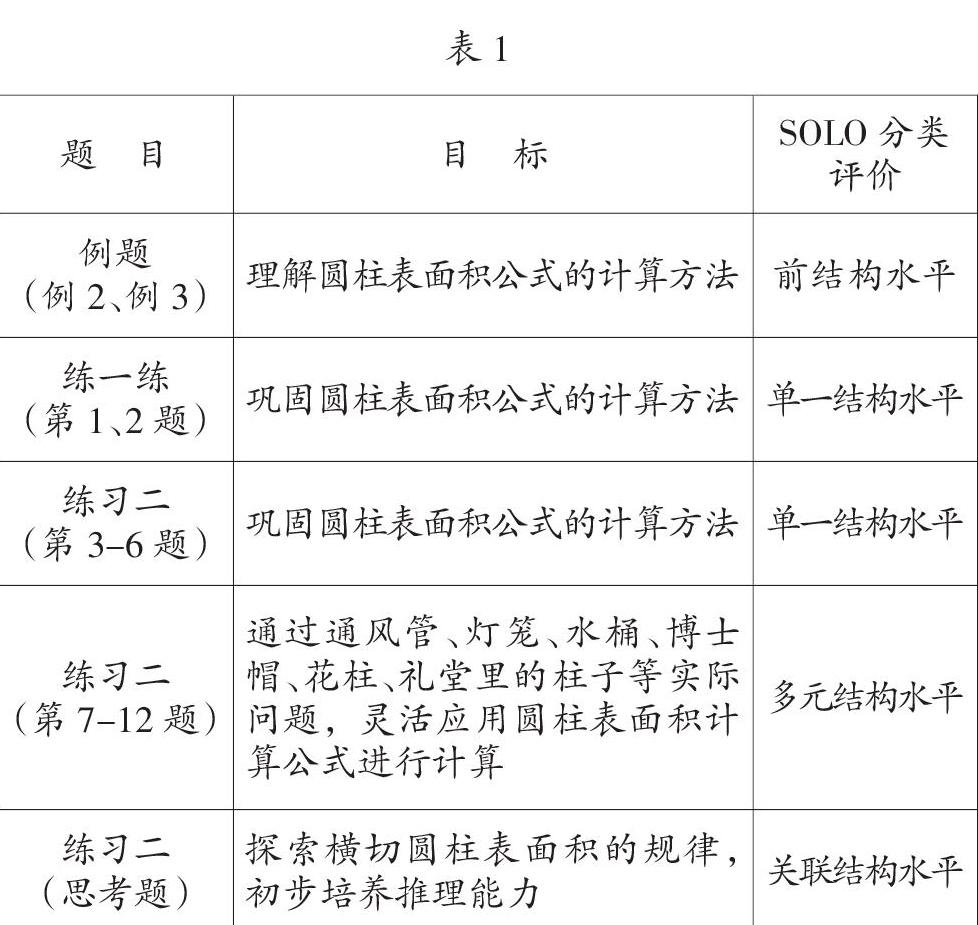
蘇教版教材在這一節內容安排了2道例題和13道練習。根據SOLO分類評價水平，筆者對這些例題和習題做了如下分析。

蘇教版數學教材的這種編排，難度層次分明，重點難點突出，“四基”導向鮮明，是一種非常理想的基礎課程。合肥市城區的六年級學生起點整體較高，每個班級至少有60%的學生在校外教育機構參加數學拓展課程學習。所以，從學生的真實學習情況來看，教材上的這2道例題和13道練習題，留給學生的經驗僅僅還停留在“求一個完整的圓柱體表面積”和“求缺少1個面或缺少2個面的圓柱體表面積”，留給學生的印象多是枯燥繁雜的計算、人為設置的單位換算、近似數如何取值等相對固化的要求。生活中，還有大量的、美妙多變的圓柱表面積問題得不到注意，與他們認知需求相適應的拓展內容得不到補充，學生的視野和思維得不到最大程度的提升，這不得不說是一種客觀而真實的缺憾。

因此，筆者綜合了圓柱表面積問題的各種情形，提煉和設計了“多變的圓柱表面積”這一拓展課，內容包括“組合圓柱的表面積”“切割圓柱的表面積”“卷旋圓柱的表面積”三個拓展內容。這三個拓展內容，基本覆蓋了小學生可以接受的圓柱表面積的所有問題，可以幫助學生“學得過癮”“學得徹底”。

二、層次性

美國教育心理學家加涅認為：“人類的學習是復雜多樣的，是有層次性的，總是由簡單的低級學習向復雜的高級學習發展，構成了一個依次遞進的層次與水平。”小學數學拓展課程，既要與基礎課程形成層次性，其自身又要具有層次性。

第一，拓展課程與基礎課程形成層次性。蘇教版數學教材上的基礎課程，重在引導學生理解表面積的計算方法，通過2道例題和13道練習題，主要訓練學生應用公式的能力，教材突出的是基礎知識和基本能力;“多變的圓柱表面積”一課不再是簡單的記憶公式、理解公式、應用公式，而是融入了分析、創造等高階思維活動，無論是解答過程、方法的復雜程度上，還是內容和思維的要求上，都有了更高的要求。

第二，拓展課程自身具有層次性。“多變的圓柱表面積”課程內容，從情境原形上看，“組合圓柱的表面積”屬于靜態問題，學生直觀可見;“切割圓柱的表面積”屬于動態問題，學生理解難度有所提高;“卷旋圓柱的表面積”則是需要借助思維想象的問題，對學生的空間觀念要求較高。這三個拓展內容，難度逐漸升級，思維抽象程度不斷遞進。從內容結論上看，“組合圓柱的表面積”規律明顯，變式不多，學情基礎好;“切割圓柱的表面積”規律較明顯，變式較多，學情基礎較好;“卷旋圓柱的表面積”規律不明顯（如用一張長方形紙，橫著卷形成的圓柱表面積比豎著卷形成的圓柱表面積小的規律是：■-■），學情基礎不足。所以，這種層層遞進的拓展課程設計，遵循了兒童學習由易到難的規律，符合兒童認知事物的基本特點。

三、典型性

設計什么樣的拓展課程，才能讓學生“見少識廣”呢？拓展課程具有良好的典型性，是不二選擇。典型課程，既要做到內容典型，還應兼顧到解決方法的典型。如果一道拓展習題能夠代表一類拓展內容，一節拓展課能夠折射一個體系的拓展精髓，是設計小學數學拓展課程的理想境界。

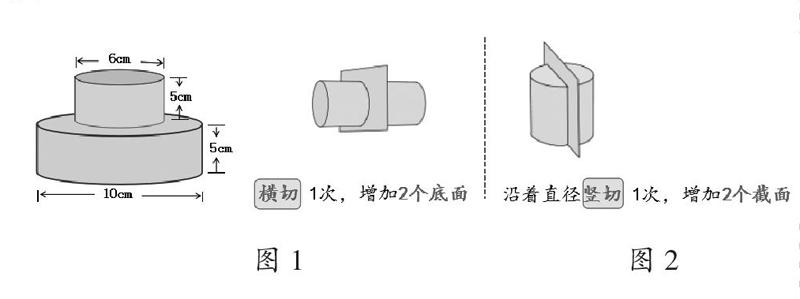
“圓柱的表面積”涉及問題多，具體的例子、情境更是數不勝數。筆者從“組合圓柱”“切割圓柱”“卷旋圓柱”三方面進行提煉，并通過典型內容的呈現，引導學生進行探究，從而發現其中的規律，掌握解決的方法，最終建立良好的數學模型。比如，在“組合圓柱的表面積”這個拓展內容中，筆者設計了求“一大一小、上下疊放的組合圓柱表面積的問題”（見圖1），并組織學生自主探究解決方法。這種組合形式是最基本的組合，當然也是最典型的組合。學生在解決這個問題的過程中，一般會出現兩種思路：思路一是“S組表=S大表+S小表-2S小底”，思路二是“S組表=S大表+S小側”。兩種思路，體現了解決組合圓柱表面積問題的兩種典型方法：“面積加減法”和“抵消轉化法”。這種典型內容和典型的解答方法，都有利于學生形成解決類似問題的“基本活動經驗”。再如，在“切割圓柱的表面積”這個拓展內容中，筆者通過與學生研究“橫切圓柱”和“豎切圓柱”后表面積變化的典型規律（見圖2），引領學生深度理解和建構“切割圓柱的表面積”問題的基本模型。

四、趣味性

如何增強拓展課程的吸引力呢？拓展課程的深度和廣度都勝過基礎課程。加強課程的趣味性，不但是基礎課程的要求，更是拓展課程的“剛需”。作為課程的設計者，我們需要準確把握不同學段兒童的興趣點，有效提升課程吸引力。比如，面對第一學段的兒童，我們可以在形式上體現趣味，以增強課程的吸引力;針對第二學段的學生，我們可以在內容上和方法上體現趣味，以更好地吸引學生參與學習。

在“多變的圓柱表面積”一課中，三個內容因為體現了三種不同的樂趣，受到了學生的歡迎。“組合圓柱的表面積”，體現“挑戰之趣”。接受最近發展區內的挑戰，是每個人與生俱來的好奇心理和進步心理。學生學習基礎課程時，一旦掌握了計算公式，接下來就是翻來覆去地應用在一個又一個圓柱上，有的要計算3個面，有的要計算2個面，還有的只要計算1個側面。學生一旦遇到需要計算兩個圓柱或者多個圓柱組合的表面積，必然會產生挑戰的樂趣，這種樂趣驅動學生主動積極地投入到一個新知探索的過程之中。“切割圓柱的表面積”，體現“思考之趣”。與基礎課程相比，把一個圓柱“橫著切”“豎著切”，而且研究“截面”，這不是像做游戲一樣，很有趣的一種思考活動嗎？在這種帶有兒童游戲色彩的思考過程中，去建構數學模型，對每位學生來說都有強烈的思考樂趣。“卷旋圓柱的表面積”，體現“操作之趣”。皮亞杰說：“兒童的智慧，發源于指端”，同樣，兒童的樂趣，也源自指端。真實可見的普通紙張，通過橫著卷、豎著卷，橫著旋轉、豎著旋轉都能形成圓柱體，這不是很神奇嗎？更重要的是，學生還能通過趣操作之后的冷思考，找到表面積大小的規律，讓好玩的操作成為探尋數學結論的素材。

小學數學拓展課程的設計，從不同的維度和視角，還有許多需要注意的地方，比如系統性問題、科學性問題、針對性問題、評價性問題等等。這些都值得我們在具體實踐中不斷探索、不斷總結，從而為兒童數學核心素養的真正落地做出我們應有的貢獻。

[責任編輯：陳國慶]