初中數學問題教學的思路探究

一、讓數學問題在體驗中解決，激發學習興趣

為了培養學生的學習興趣，調動學生的學習積極性，可以讓學生親自動手檢驗數學知識。學習簡單而直接的問題，學生只是簡單被動的接受，思考欲望會很低，甚至為零。如果能讓學生實踐操作，學生的積極性便會大大提高，解決問題的能力也會大大增強，對于知識的掌握也會更加牢固。

例如，在探究“最短路徑問題”這一節課時，有這樣一個問題：從線段A到線段C之間有很多條路可以選擇，那么，從A點到C點怎樣走路程最近呢？(如圖1)問題的解決可以讓學生到黑板上來操作，用細繩根據圖中所示的路線進行測量并比較，最后看出連接A、C之間的直線是最短的，進而得出結論“兩點之間線段最短”。當教師拿出細線問：“誰來到黑板前測量一下這幾條線呢？”問題一提出，學生便仿佛脫離了課堂，并置身于實際生活中，因而迫不及待想尋找解決問題的辦法，急于找出這一最短的路徑。讓學生動手實踐操作，會極大調動學生學習的熱情，不必說學生爭先恐后地想到黑板上去演示，就是坐在下面觀察的學生也會目不轉睛，不放過任何一個細節。這樣學到的知識記憶更加深刻，甚至會終生不忘。

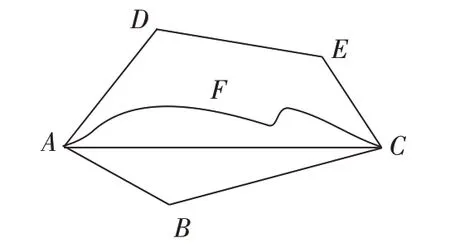
圖1

二、把數學問題置于生活實踐中，掌握問題規律

把數學知識運用于生活，創設問題情境，在生活中體現數學理念。問題情境的創設要充分考慮學生的認知、情感、性格、興趣等多方面因素，問題的設計要貼近學生實際生活，將學生需要掌握的數學知識與現實生活緊密聯系起來。只有在生活化的學習情境中去感知，才能使學生切實明白知識的價值，同時讓學生在熱情與挑戰中探尋到數學問題的規律性。

設計這樣的問題：某村在公路一側有一菜園A，另有一深水井B，每年干旱季節都要對菜園進行人工澆灌，由于菜園在高坡地，需要在公路一側安裝一加壓泵站M，那么泵站建在公路何處才能使從深水井到菜園鋪設的水管最少呢？(如圖2)

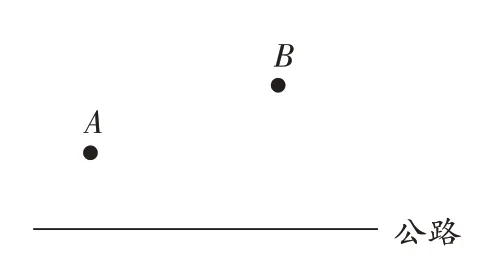
圖2

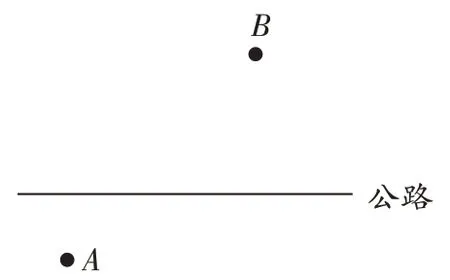
圖3

根據《課標》的要求，數學問題的設計既要保證問題的探索性，又要具備思維的延展性和形象的趣味性。把數學知識置于生活實際中，探索解決此問題的方法作為最終目標，為本節課埋下伏筆，設置懸念，激發學生解決問題的的主動性和戰勝困難的挑戰性。

回顧舊知，用“兩點間線段最短”這一理論來解決這一問題，指引知識點的應用，打開學生思維的大門。接下來再引出與問題1 相似的問題：如果深水井A和菜園B在公路的兩側，那么在公路何處修建泵站所用管道最短呢？(如圖3)依照剛才的思路，這個問題也會迎刃而解——連接AB交于公路一點M，那么就找到了泵站修建的位置。把到生活中尋找解決問題的方法作為這節課的目標，使學生在輕松愉悅的氛圍中積極主動地探索數學的奧妙，并找到數學的規律。

三、讓數學問題在探究中生成，提升總結能力

數學知識不是單一的孤立存在的，知識的輸入要注重知識的發生、發展過程，問題的設計要適宜改變，體現過程變式教學策略。進階式引向深入，提升學生多角度理解問題的能力，引導他們對教學內容的主動建構和有效遷移。運用學過的知識不斷進行探究，不僅會激發學習的興趣，還會提升解決問題的能力。

為解決本節圖2 的問題，可以再設計這樣的問題進行探究：如果在公路兩側都有一口深水井B和B′，并且關于公路對稱，我們嘗試連接AB′，交公路于點M，比較一下AM+MB與AB′的數量關系，會有什么發現？(如圖4)

通過教師思維引導，學生的積極探索，不僅發現了AM+MB與AB′的數量關系，而且探究總結出關于對稱圖形的幾個性質，結合合圖3 和圖4 的思路，找到了解決圖2 問題的解決方案，從而達到本節的教學目標。通過探究，可以找到問題的實質，讓學生在探究中發現規律，提高總結問題的能力。

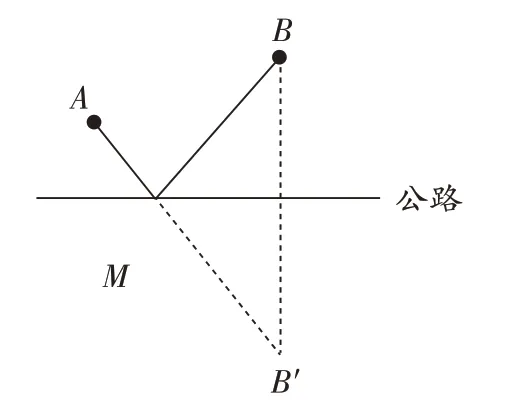
圖4

問題教學是數學研究的出發點，是引導學生學習數學的一把鑰匙。因此，在課堂教學中要注重數學問題的提出與解決，要充分體現學科核心素養中彰顯學生主體地位的核心理念，讓學生在數學學習的道路上越走越寬。