基于損傷塑性本構模型的上承式梁拱組合剛構梁拱交匯節點極限承載力研究

丁艷超，向中富，李亞勇，張雪松，周 銀

(1. 重慶交通大學 土木工程學院，重慶 400074； 2. 中建隧道建設有限公司，重慶 401320)

0 引 言

大跨徑梁拱組合剛構橋融合了拱橋、梁橋優點，克服了連續剛構橋的開裂與下撓問題，是梁橋與拱橋的結合[1]。目前國內外已建有大量預應力混凝土連續剛構橋，其中1997年建成廣東虎門大橋輔航道橋，以主跨270 m居世界之首。隨著連續剛構橋服役年限增加，箱梁裂縫與跨中下撓病害日益加劇，部分橋梁也因此喪失了使用功能而退出了歷史的舞臺。鑒于此，近年來國內新建連續剛構橋的主跨基本都小于200 m。梁拱組合剛構相比于常規連續剛構橋挖去了主梁根部腹板混凝土，降低了混凝土用量，有效改善了常規剛構橋跨中下撓問題，并可以將預應力鋼筋混凝土橋梁主跨提升至350 m，在同等跨徑級別，具有經濟效優勢[2]。梁拱組合剛構橋具有諸多優點的同時，結構本身存在多個受力復雜的節點，筆者著重對梁拱交匯節點展開基于CDP模型(concrete damaged plasticity model)的極限承載能力[3-5]研究。

1 工程概況

禮嘉嘉陵江大橋為梁拱組合剛構橋，跨徑布置為140+245+190+130+80 m，主橋采用雙幅布置形式，標準斷面單幅寬18.05 m，單幅布置為：2.0 m(檢修兼人行道)+15.5 m(機動車道)+0.55 m(防撞護欄)=18.05 m，兩幅之間設1.9 m中央分離帶，橋型布置如圖1。

采用Midas/Civil建立禮嘉嘉陵江大橋整體桿系有限元模型，創建858個梁單元，56個桁架單元(施工過程輔助措施，成橋拆除)，994個節點，128個施工階段，采用M法創建樁土效應邊界條件，汽車荷載為城-A級，采用5車道最不利汽車加載，同時考慮人群、溫度、制動力等作用，模型如圖2。

2 損傷塑性模型本構關系

Abaqus內置的CDP模型本構模塊可以很好的模擬混凝土的損傷過程，參考GB50010—2010《混凝土結構設計規范》[6]建立混凝土的單軸拉壓本構關系曲線。

2.1 混凝土單軸應力應變關系

混凝土本構關系如圖3，混凝土單軸受壓與受拉的應力-應變曲線方程如下：

1)混凝土單軸受壓的應力-應變曲線方程如式(1)～(3)：

σ=(1-drc)E0ε

(1)

(2)

(3)

2)混凝土單軸受拉的應力-應變曲線方程如式(4)～(6)：

σ=(1-drt)E0ε

(4)

(5)

(6)

式中：E0為混凝土初始彈性模量；fck、ftk為混凝土單軸抗壓與抗拉強度標準值；εc、εt為峰值壓與拉應變；drc、drt為混凝土單軸受壓與受拉損傷演化參數。

2.2 屈服準則

混凝土塑性損傷模型的屈服面函數[7-11]如式(7)～(8)：

(7)

(8)

式中：I1、J2分別為應力張量第一不變量與偏應力張量第二不變量；σb0、σc0分別為混凝土雙軸與單軸抗壓強度；σt0為混凝土單軸抗拉強度；Kc為控制混凝土屈服面在偏平面上投影形狀的參數，對正常配筋混凝土Kc=0.67。

2.3 流動法則

CDP模型采用非關聯流動法則[12-15]，其塑性勢函數如式(9)：

(9)

式中：φ為混凝土屈服面在強化過程中的膨脹角，取值范圍為37°～42°；λ為混凝土塑性勢函數的偏心距，取0.1。

3 局部模型力邊界條件

梁拱組合剛構橋結合了梁橋與拱橋的受力特點，整體結構計算模式明確，但在梁拱組合節點位置，結構受力復雜。為保證結構施工與運營階段結構安全，筆者基于混凝土塑性損傷機理，對梁拱組合節點位置進行局部分析[16-17]，并討論其極限承載力。梁拱組合節點構造如圖4，上弦梁為49～56號單元，下弦拱為1 024～1 026號單元。目前，局部分析普遍采取從桿系整體模型中提取的局部模型力邊界條件，或位移邊界條件施加在局部模型邊界上的方法。此法對于簡單結構，如連續剛構0號塊分析，具有較高的實用性且計算精度較高。但針梁拱組合節點的復雜結構，盲目的采用上述方法，無法實現結構受力狀態的真實模擬，主要有以下兩點原因：① 節點構造復雜，整體模型中在局部模型端部節點與關心部位間可能存在外荷載；② 圖4中梁拱組合節點在局部模型與整體模型中的邊界差異較大，直接提取的端部節點內力作為力邊界條件，無法保證關心部位(圖4中O點為51j截面)內力狀態與整體模型等效。筆者提出一種基于Von-Mises應力相似的方法，創建局部模型力邊界條件。

復雜結構局部分析的核心，是建立與整體模型受力狀態相同的局部桿系模型[18]。但在實際工程中幾乎無法建立這種局部模型，只能尋找與整體模型最大程度相似的局部桿系模型，進而采用通用有限元程序，進行局部結構的空間實體分析。

在方法實施中需要注意：① 即使通過影響矩陣分析滿足了51j與1026j截面的內力狀態與目標狀態相同，但52i截面的內力狀態仍有較大的偏差，通過思路中②～④消除52i截面內力偏差對計算結果影響；② 變量Gx(-x方向)與Gz(-z方向)分別用于調節52i截面Fx與52j截面My。

3.1 荷載組合

從極限承載能力角度出發，根據最不利受力原則構建了18個荷載組合，最不利荷載組合計算如式(10)：

(10)

式中：S恒為恒荷載；Sqc為汽車荷載；Srq為人群荷載；Sgs1為鋼束一次荷載；Sgs2為鋼束二次荷載(包括在恒荷載中)；Sxb2為徐變二次荷載；Sss2為收縮二次荷載；Ttotal為整體升降溫；Ttd為正負溫度梯度；Szd為制動力荷載；Scj為支點沉降荷載。各荷載組合系數取1.0。

18個荷載組合分別為梁拱組合節點51j、52i、1026j這3個位置(圖4)的軸力Fx、剪力Fz、彎矩My的最大與最小組合。其中汽車與人群荷載采用Midas/Civil移動荷載追蹤功能提取，18個荷載組合表1。

表1 梁拱組合節點最不利荷載組合

3.2 節點內力平衡分析

Von-Mises應力最大相似追蹤法采用影響矩陣分析法保證了圖4中51j截面與1026j截面內力與目標內力狀態相同。但51j節點位置(51號單元j節點與52單元i節點為同一個節點)由于節點外力的存在，致52i截面內力與目標內力狀態不同，筆者引入節點內力平衡分析法，辨識影響節點內力平衡關鍵因素，成為了構建合理局部桿系模型的關鍵，如圖4。可基于節點內力平衡原理以51j和1026j截面內力為變量求解52i截面內力，具體見公式(11)，依據公式(12)評判影響節點內力平衡的因素。

(11)

(12)

根據表2繪制出四川旅游團餐游客滿意度IPA分析四象限圖(圖1).IPA分析圖以重要性為橫軸(X軸)，以滿意度為縱軸(Y軸).可以看出，樣本中游客對四川旅游團餐的重要性的感知平均分值為3.87，處于“重要”的程度，滿意度的感知平均分值為3.42，處于“滿意”的程度，說明游客對四川旅游團餐的感知評價從整體上來說持有積極的態度;從二者的比較均值差來看，游客對四川旅游團餐的滿意度指標雖然較好，但其均值全部低于重要性指標均值，這也指出四川旅游團餐的服務質量仍存在提升的空間.

表2 節點內力平衡因子

表2中可以看出，S恒、Sgs1、Sgs2、Sss2、Ttotal、Ttd分別不同程度的影響著節點內力平衡節點內力平衡。在不考慮汽車集中荷載存在的情況下，依然有多因素共同影響著節點內力平衡。依據圣維南原理，進行局部分析的前提是局部范圍內不能有集中荷載。要想實現局部桿系模型內力狀態與整體模型相同幾乎無法實現。

眾多因素中Sgs1影響最顯著，引起的內力偏差絕對量值相對較大。按照鋼束是否穿過52i截面可將Sgs1分為I類鋼束與Ⅱ類鋼束，不難發現圖4中Ⅰ類鋼束是引起ηgs1顯著的主要成分，因此筆者提出通過微調Ⅰ類鋼束組合系數，以削減不平衡內力對52i截面Von-Mises應力的影響。

3.3 實例驗證

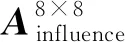
(13)

(14)

3)分別求解52i截面內力偏差ΔFx、ΔFz、ΔMy對圖5中5個點Von-Mises應力的影響，判斷ΔFx為顯著影響因素。經多次調整Ⅰ類鋼束的組合系數，降低內力偏差對梁拱組合節點最不利位置Von-Mises應力的影響，具體如表3。

表3 Von-Mises應力追循環追蹤

4)通過Von-Mises應力最大相似追蹤法獲得的局部模型具有如下特點：① 51j、1026j截面三個方向內力與表1相同；② 52j截面軸力、彎矩與表1相同；③ 52i截面軸力與表1相同，另外方向內力與表1存在小幅的偏差，但局部模型中最不利位置1#-5#點的Von-Mises與整體模型極大程度相似。

18組局部模型的力邊界條件如圖6。

4 梁拱組合節點局部有限元分析

運用Abaqus建立1/2梁拱組合節點局部實體單元模型，在上下弦主梁分別施加力邊界條件，在另一邊施加固定約束，如圖4。對稱面施加對稱邊界，采用CDP模型進行混凝土材料非線性分析，混凝土采用C3D8R單元，預應力鋼束與普通鋼筋采用T3D2單元，以Embedded方式嵌入混凝土中，未考慮鋼束與混凝土之間的滑移現象，采用降溫法模擬預應力荷載，有限元模型如圖7。圖7(b)中下彎曲線為預應力鋼束，其余為普通鋼筋。

根據圖4建立18個Abaqus實體單元模型，通過計算繪制出了圖6所述18個荷載組合的荷載位移曲線，如圖8。發現荷載組合3與荷載組合8對梁拱組合節點最為不利，均為上弦梁最大正彎矩最不利組合工況。

圖9為荷載組合3作用下梁拱交匯節點不同荷載因子受拉損傷云圖，由圖8、圖9可知：① 荷載因子小于1.0時，荷載位移曲線接近直線，結構剛度恒定，梁拱組合節點未受到損傷；②上弦梁最大正彎矩組合3-51jMy,max與9-52iMy,max是梁拱交匯節點最不利且起控制作用的荷載工況，極限承載因子為2.012；③極限承載力計算結果與JTG D60—2015《公路橋梁通用設計規范》基本一致，極限承載因子大于1.4，并有一定的安全儲備；④圖9可以看出，梁拱組合節點的破壞過程及破壞路徑。結構從上弦梁底板混凝土受拉破壞開始，隨著荷載的增大破壞面逐漸擴展至上弦腹板，最終上弦梁結構被拉潰。

5 結 論

筆者針對上承式梁拱組合剛構梁拱組合節點展開了18組考慮材料非線性的局部實體有限元分析，繪制了18個最不利工況的荷載位移曲線，研究了影響梁拱組合節點內力平衡影響因素，通過計算與對比分析，得到如下結論：

1)18個不利荷載工況中，梁拱交匯節點處上弦梁最大正彎矩組合是最不利且起控制作用的荷載工況。最不利荷載工況下梁拱組合節點極限承載因子為2.012，計算結果與規范JTG D60—2015《公路橋梁通用設計規范》一致，極限承載因子大于1.4，并有一定安全儲備。

2)梁拱交匯節點的破壞路徑為：從上弦梁底板混凝土受拉破壞開始，隨著荷載增大破壞面逐漸擴展至上弦腹板，最終上弦梁結構被拉潰。

3)提出了一種基于Von-Mises應力相似追蹤的方法，可有效模擬實體單元力學邊界條件。

4)給出了判斷節點內力平衡的計算公式，提出內力平衡影響因子η，并通過數據對比給出了影響因子相應的的閾值范圍，定量解釋了局部桿系模型與整體模型的內力狀態無法相同的原因。