2-PUR-PSR并聯機構尺度綜合多目標優化

張偉中 李金平 葉 敏 楊 超

(1.浙江理工大學機械與自動控制學院, 杭州 310018; 2.浙江機電職業技術學院自動化學院, 杭州 310058;3.新南威爾士大學土木與環境工程學院, 悉尼 NSW 2052; 4.長安大學工程機械學院, 西安 710064;5.嘉興學院機電工程學院, 嘉興 314001)

0 引言

少自由度并聯機構具有結構簡單、高承載能力、高剛度、高精度以及優異的運動/力傳遞性能和動態性能等優勢，有效地彌補了串聯機構的不足[1-3]。其中，三自由度兩轉一移(Two rotations and one translations，2R1T)并聯機構已廣泛應用于諸多領域，如Z3主軸頭[4]、Exechon機器人[5-6]、Tricept并聯機床[7]和振動篩[8]等。

盡管2R1T并聯機構得到了廣泛的應用研究，但該類機構的優化設計問題仍未得到很好的解決。運動學性能評價指標和參數優化算法是機構運動學優化設計的主要內容[9-11]。

由于并聯機構工作空間相對較小，機構性能優化設計首先需考慮通過優化設計變量獲得更大的規則工作空間[12-15]。MASORY等[16]在考慮關節轉角約束、桿長約束及桿件干涉的基礎上，采用數值積分方法得到了較為接近實際的機構工作空間。CARBONE等[17]采用二進制表達方法得到了可達工作空間體積的數值表達式。RAMANA等[18]采用極坐標方法得到了規則工作空間的最大內切圓柱體積的表達式。BOUNAB[19]計算了Delta并聯機構的規則圓球工作空間體積。以上研究將可達工作空間或圓柱、圓球作為規則空間，沒有考慮不同高度下的工作空間最大化。

性能分析是并聯機構進行尺度綜合的前提，而構建合理的運動學指標是并聯機構運動學性能分析的重要基礎。GOSSELIN等[20]以雅可比矩陣條件數作為機構的性能評價指標。陳修龍等[21]以雅可比矩陣的奇異值作為性能指標，對并聯機器人進行結構優化設計。對于混自由度并聯機構(包含移動和轉動)，雅可比矩陣中的元素量綱并不統一，直接計算上述指標會導致機構性能物理意義上的模糊和解釋錯誤。LIU等[22-23]提出了運動/力性能傳遞指標，該指標具有量綱統一、與坐標系無關、可判斷機構的奇異位置等優點，該運動學指標在很多機構分析中得到應用。

尺度綜合是以性能指標為衡量標準對機構的尺寸參數進行優化設計，目前主要借助空間模型法對機構進行尺度綜合[24]。在工程應用中，往往需要借助智能優化算法對并聯機構進行多目標優化，以達到多個目標的綜合最優。ZHANG等[25]使用差分進化算法使3-UPU并聯機構的剛度和可達工作空間最大化。崔國華等[26]基于Isight優化了3-UPS-S并聯機構的工作空間、靈巧度、承載能力和剛度。孫小勇等[27]通過優化數學模型對6-PSS并聯機構的工作空間和動力學性能進行了多目標優化。ZHANG等[28]使用遺傳算法對球形機構的全局條件數和工作空間進行了多目標優化。

本文以2-PUR-PSR并聯機構為例，對其進行結構參數的優化設計，在運動學模型分析基礎上，結合螺旋理論，以規則圓臺工作空間和全局運動/力傳遞性能為目標函數，以關節轉角和驅動限制為約束條件，采用多目標粒子群優化算法進行尺度綜合多目標優化設計，得到滿足工作條件的機構規則工作空間和運動/力傳遞性能的Pareto最優，為得到性能更優的機構提供設計依據。

1 機構描述與運動學分析

1.1 機構描述

如圖1所示，由機架、動平臺、兩條結構完全相同的PUR分支和一條PSR分支組成了2-PUR-PSR并聯機構。該機構是為了減小由內副驅動的2-UPR-SPR并聯機構在操作過程中的運動質量，并提高機構的剛度進行構型綜合，提出的一種由外副驅動的兩轉一移并聯機構[29-30]。機構由固接于機架導軌上的線性驅動器驅動[31-32]。

圖1 2-PUR-PSR并聯機構Fig.1 2-PUR-PSR parallel manipulator

通過驅動P副，3條分支結構與機架的導軌相連。在2條PUR分支結構中，U副的第1個轉軸共線，且與其P副的移動方向一致；U副的第2個轉軸則垂直于P副的移動方向，同時平行于另一端和動平臺相連接的R副軸線方向；并且PUR分支的兩個R鉸軸線互相平行。S鉸是PSR分支與基座相連的點，并與動平臺相連的R鉸軸線與B1B2平行。其中：Ai表示分支i(i=1, 2, 3)中與基座相鄰運動副的中心，A1、A2、A33個點在同一水平面內。分支1、2中虎克鉸中心用B1、B2表示；分支3中與動平臺相鄰的轉動副中心用B3表示。

2-PUR-PSR并聯機構定/動坐標系原點為A1A2中點，x軸指向A2點，y軸指向A3點，z軸遵循右手法則，從而建立固定坐標系Oxyz。與此同時，以B1點為原點，指向B2點為u軸，垂直于u軸且位于面B1B2B3內為v軸，w軸遵循右手法則，從而在動平臺上建立局部坐標系puvw。以A1A2的中心點O為原點，與OA3共線為x軸，沿著OA1方向為y軸，由右手螺旋法則確定z軸，建立定坐標系Oxyz。以B1B2的中心點為原點，與oB3重合為u軸，指向點B1為v軸，由右手法則確定w軸，建立動坐標系ouvw。

對2-PUR-PSR并聯機構的結構參數定義為：oB1=oB2=l1,oB3=l2,A1B1=A2B2=l3,A3B3=l4，并且為減少尺寸參數的個數，假定滿足l1l4=l2l3。采用文獻[33-34]提出的螺旋理論對機構進行分析，可求得2-PUR-PSR并聯機構為三自由度機構，分別是2個轉動和1個移動自由度。

1.2 位置逆解

已知2-PUR-PSR機構末端點o的位置矢量為p=(x,y,z)T，求解驅動P副的移動距離即為機構的位置逆解問題。

由圖1可知，在2-PUR-PSR并聯機構中，動坐標系ouvw相對于定坐標系Oxyz的姿態可表示為

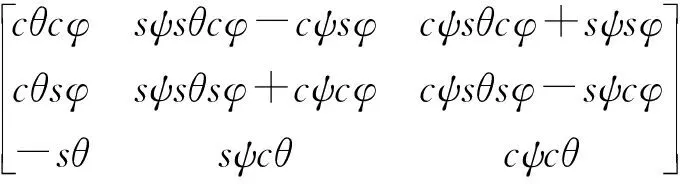
(1)

式中Rz(φ)、Ry(θ)、Rx(ψ)——繞z軸、y軸、x軸的旋轉矩陣

c表示余弦函數，s表示正弦函數。

根據圖1可得，閉環矢量方程為

qi=p+bi-ai(i=1,2,3)

(2)

式中，分支i驅動器的位置矢量為qi；從點Ai到Bi和從點o到Bi的位置矢量，分別表示為ai和bi,且bi=Rbio，oBi位置矢量在動坐標系{o}下表示為

(3)

同時，ci=Rcio是分支i中R鉸軸線的方向矢量，cio為ci在動坐標系ouvw中的方向矢量，表示為

(4)

機構分析可知，機構在運動過程中，各分支的R副軸線始終與qi-p垂直，因此可得

(5)

展開可得各分支的約束關系

xcθcφ-(q1-y)cθsφ-zsθ=0

(6)

xcθcφ+(q2+y)cθsφ-zsθ=0

(7)

y(cψcφ+sψsθsφ)+(q3-x)(cψsφ-sψsθcφ)

(8)

式(6)、(7)相減可得

(q1+q2)cθsφ=0

(9)

在運動過程中，q1+q2不可能恒等于0，為此

cθsφ=0

(10)

式(10)代入式(6)中，可得

xcθcφ-zsθ=0

(11)

由式(11)可得，假定cθ=0，則恒有z=0，這不符合機構的實際運動情況，故sφ=0，φ=0或φ=π。根據2-PUR-PSR并聯機構的結構特征，φ不可能等于π，因此φ恒為0。將該結果代入式(8)中，可得

ycψ-(q3-x)sψsθ+zsψcθ=0

(12)

綜合式(11)、(12)，位置矢量p=(x,y,z)T中的x和y可表示為

(13)

將式(13)代入式(2)中，得到2-PUR-PSR并聯機構的位置逆解為

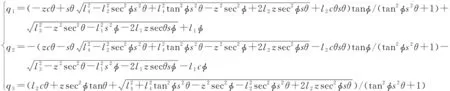
(14)

2 規則工作空間指標

規則工作空間是并聯機構的一個重要指標，可以作為優化目標函數之一。在研究規則工作空間之前有必要先對機構的可達工作空間進行研究。并聯機構的可達工作空間是指在物理約束下機器人至少從一個方向可以達到的所有點的集合。影響并聯機構工作空間的主要因素包括機構的結構尺寸、鉸鏈的轉角范圍、驅動的限制以及各支鏈之間的干涉等。

采用極坐標的方法計算2-PUR-PSR并聯機構的規則圓臺工作空間體積[19]。首先，利用空間搜索法得到可達工作空間的形狀，為下一步計算規則工作空間做準備。其次，將操作平臺高度劃分為n層。最終，計算每一個操作平臺高度下可達空間的最大內切圓半徑。得到了每一層的最大內切圓半徑后便計算規則圓臺的工作空間體積，計算公式為

(15)

式中Ai——第i層最大內切圓的面積

Δz——層間的高度間隔區間

給定2-PUR-PSR并聯機構的物理約束為

(16)

式中，qmin=50 mm和qmax=800 mm分別為驅動的最小和最大限制，αi1和αi2分別表示第i分支的R鉸和U鉸的轉角，其可以通過運動學分析得到

(17)

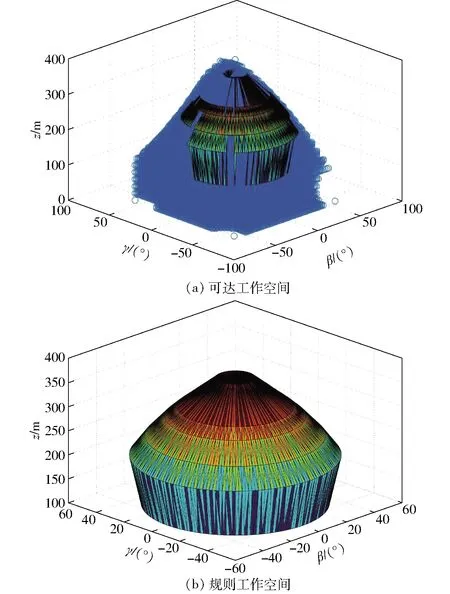
圖2 2-PUR-PSR并聯機構工作空間Fig.2 Workspaces of 2-PUR-PSR parallel manipulator

式中，nli、npi、nbi表示桿件、動平臺法線和定平臺法線的單位矢量。2-PUR-PSR并聯機構在優化前的初始機構參數為l1=l2=200 mm,l3=l4=400 mm。本文采用空間搜索法給出機構的可達離散工作空間如圖2所示，可達工作空間關于γ=0°對稱，與2-PUR-PSR并聯機構的結構吻合。可達工作空間的形狀和尺寸不規則，不利于軌跡的規劃和算法控制。實際工程應用中一般采用規則工作空間，不失一般性，本文采用每一給定操作平臺高度下可達空間的最大內切圓構成的圓臺作為機構的規則工作空間，如圖2所示，為了確保末端執行器的姿態要求，此處將內切圓的最小半徑設置為10°。

3 運動/力傳遞性能

3.1 局部傳遞指標

并聯機構的本質作用之一是在機構的輸入端和輸出端之間傳遞運動和力。研究者據此特性，定義相應的能夠同時體現運動和力的傳遞能力的指標，用以分析并聯機構的運動/力傳遞特性[35-36]。

陳祥等[37]根據力傳遞性能與傳動角的密切關系，提出利用運動/力傳遞指標(LTI)作為運動學性能評價指標，利用該指標表示機構從輸入到輸出的傳遞效率。LTI指標可表示為

(18)

(19)

式中λi——分支i的輸入傳遞指標(ITI)

ηi——輸出傳遞指標(OTI)

$Ai——分支i的輸入運動螺旋(ITS)

$Oi——分支i的輸出運動螺旋(OTS)

$Ti——分支i的傳遞力螺旋(TWS)

從式(18)、(19)中可知λi和ηi的取值范圍均為0～1；同時值越接近于1，機構的運動/力傳遞性能越好。對ITI和OTI綜合考慮，局部運動/力傳遞指標(LTI)可以表達為

LTI=min{λi,ηi}

(20)

從式(20)可以看出，LTI計算值的范圍為0～1，是一個與坐標系無關的無量綱指標，其值越接近1，表示能量從機構輸入端到輸出端的傳遞效率越高。

如圖1所示，以機構分支1為例，其運動螺旋系和約束螺旋表達式為

(21)

(22)

由于機構分支1的驅動關節為P副，為此$A1=$11。傳遞力螺旋$T1與機構分支1中被動關節的互易積為零，即

$T1°$1i=0 (i=2,3,4)

(23)

通過式(21)、(23)可計算得傳遞力螺旋$T1表達式為

$T1=(a1/|a1|;q1×a1/|a1|)

(24)

式中 $T1——過點A1、沿a1方向的力螺旋

同理，其余2個分支的傳遞力螺旋分別為

$T2=(a2/|a2|;q2×a2/|a2|)

(25)

$T3=(a3/|a3|;q3×a3/|a3|)

(26)

式中 $T2——過點A2、沿a2方向的力螺旋

$T3——過點A3、沿a3方向的力螺旋

鎖住機構除分支1之外的所有驅動關節，機構分支2和3中的傳遞力螺旋轉變成約束螺旋，機構的約束螺旋系為U1=[$C1$C2$C3$T2$T3]，其維度為5，此時機構為單自由度機構，動平臺的瞬時運動可通過輸出運動螺旋表示為

$O1°U1=0

(27)

式中 $O1——過點A3且沿A2A3方向的運動螺旋

由式(27)可得輸出運動螺旋的表達式為

$O1=
((q3-q2)/|q3-q2|;q2×(q3-q2)/|q3-q2|)

(28)

同理，其余兩種情況的輸出運動螺旋也可通過該方法得到，分別表示為過點A3且沿A1A3方向和過點A1且沿A1A2方向的運動螺旋。

3.2 全域傳遞指標

由于LTI指標僅能判斷機構在單個位形下的運動/力傳遞性能，而機構往往在一個特定的工作空間內運行，需要在一個工作空間內去評價機構的運動/力傳遞性能。為此，定義全局傳遞指標(GTI)去評價機構在全域的運動學性能指標，表達式為

(29)

在實際計算過程中，采用離散點的數值方法計算GTI，表達式為

(30)

式中n——規則工作空間的離散點的數量

GTI指標越高，意味著機構的運動學性能越好。

4 多目標優化

多目標優化是指同時優化彼此互相沖突的多個目標函數，多目標優化問題的解不唯一，而是一組均衡解，稱為非劣解集或Pareto最優解集，且這組解無差別。它是由任一個目標函數值的提高都必須以犧牲其他目標函數值為代價的解組成的。所謂非劣解是指由這樣一些解組成的集合(又稱非劣解集)：與集合之外的任何解相比它們至少有一個目標函數比集合之外的解優，而其他目標函數又不比集合之外的解差。本文以第2節和第3節構建的規則圓臺工作空間和GTI作為目標函數，為了將目標函數值控制在同一個量級，將工作空間的體積乘以系數10-3，多目標優化的數學模型為

(31)

其中xdmin=(150， 150， 350)mm

xdmax=(250， 250， 450)mm

式中xd——設計參數矢量

為了求解式(31)的多目標優化問題，采用多目標粒子群(MPSO)優化算法，粒子群(PSO)算法的基本思想是模擬鳥群的覓食行為，群體中每一個體被看作一個在D維搜索空間中沒有體積和質量的“粒子”，空間的維數D即為自變量的個數。每一個粒子通過跟蹤兩個極值來更新自身的空間位置和飛行速度，其中一個極值為單個粒子在自身迭代過程中的最優解粒子，稱為個體極值；另一個極值為種群在迭代過程中的最優解粒子，稱為全局極值。迭代的過程中粒子會根據自身經驗(個體極值)和種群交流(全局極值)來調整搜尋方向和速度，直至找到全局最優解。粒子群算法根據自己的速度決定搜索，替代了遺傳算法復雜的交叉和變異操作，具有收斂速度快的優點。

假設種群由N個粒子組成，在D維搜索空間進行搜索，第i個粒子的個體最優位置記為pi=(pi1,pi2,…,piD)(i=1，2，…，N)，全局最優位置記為pg=(pg1,pg2,…,pgD)，粒子根據這兩個最優值更新自己的速度和位置，即

vij(t+1)=ωvij(t)+c1r1(t)(pij(t)-xij(t))+
c2r2(t)(pgi(t)-xij(t))

(32)

xij(t+1)=xij(t)+vij(t+1)

(33)

式中ω——動態慣性權重

c1、c2——學習因子，表示粒子跟蹤自己歷史最優值和全局最優值的權重

r1、r2——分布于[0,1]區間的隨機數

式(32)的第1部分表示粒子之前的速度，用于保證算法的全局收斂性，第2、3部分保證算法具有局部收斂的能力。采用的粒子群優化算法參數設置如表1所示。

圖3給出了多目標優化的Pareto前沿，左下角區域的解屬于被支配解，右上角區域的解屬于不可達到的解。由圖可以看出，由于多目標之間的競爭和耦合關系Pareto前沿并不是光滑的曲線分布。圖中運動學/力傳遞性能GTI與Vr成反比，GTI越大，Vr越小。說明GTI與Vr關于結構的幾何參數存在競爭關系，無法在Pareto前沿上得到運動學性能與工作空間體積均取得最優的情況，設計人員需要根據兩者的權重在Pareto前沿上得到兩者的均衡點，從而減少了設計時間。

表1 粒子群優化算法的參數設置Tab.1 Parameter setting of particle swarm optimization algorithm

圖3 目標函數Vr和GTI的Pareto前沿Fig.3 Pareto front of objective functions Vr and GTI

表2給出了Pareto前沿的18組最優解集以及優化前的機構參數及目標函數值。第1組對應的設計參數(151.92，150.50，402.17)mm對應的工作空間的體積達到了極值582 rad2·mm，比優化前提高了37.59%，GTI卻只有0.458；第2組設計參數(169.60，219.09，449.09)mm對應的GTI達到了極大值0.687，比優化前提高了57.57%，但縮小了工作空間的體積。也就是說2-PUR-PSR并聯機構的運動學性能與工作空間之間存在著競爭關系，不能同時達到兩者的最優，需要工程人員根據需要在兩者之間做出取舍。

不失一般性，圖4給出了優化后的第2組設計參數在平面z=0.25 m中的LTI指標分布圖，可以看出指標關于ψ=0對稱，這與機構的對稱性是吻合的。圖中還可以看出，LTI的最大值不是在初始位置(ψ,θ)=(0°,0°)處而是發生在(γ,β)=(0°,10°)附近的位置。

基于參數優化結果，并考慮加工與裝配工藝性，選取其中1組結構參數尺寸，給出該2-PUR-PSR并聯機構的設計方案，繪制三維模型圖，加工制作樣機如圖5所示，該機構驅動器均設置在裝置的機架上，機構運動時電機不會跟隨機構桿件一同運動，從而減輕了機構運動質量，進而減輕了裝置的負荷，提高了裝置的驅動能力。因此，這種機構具有較好的運動穩定性、實時控制性強等優點。

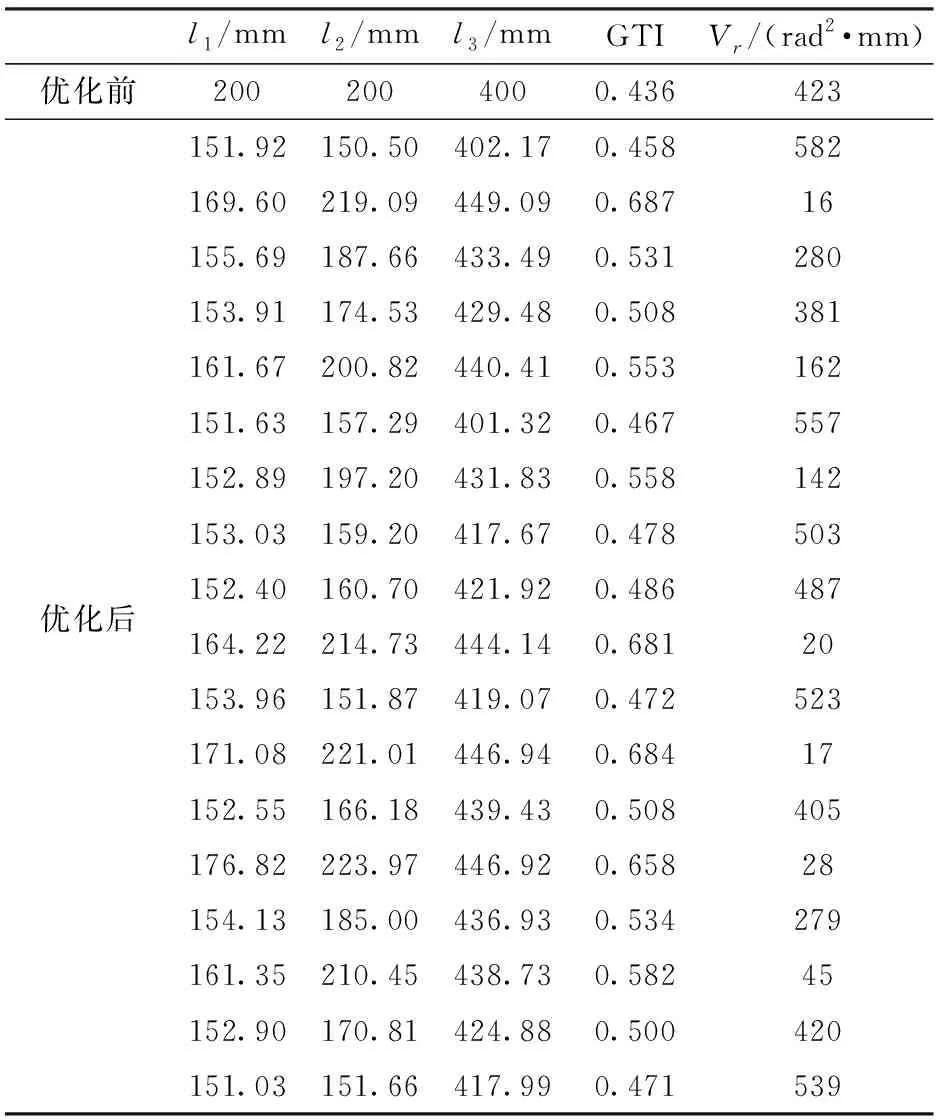
表2 Pareto前沿的最優解集以及優化前的機構參數及目標函數值Tab.2 Optimal solutions and optimization of Pareto frontier and previous mechanism parameters and objective function values

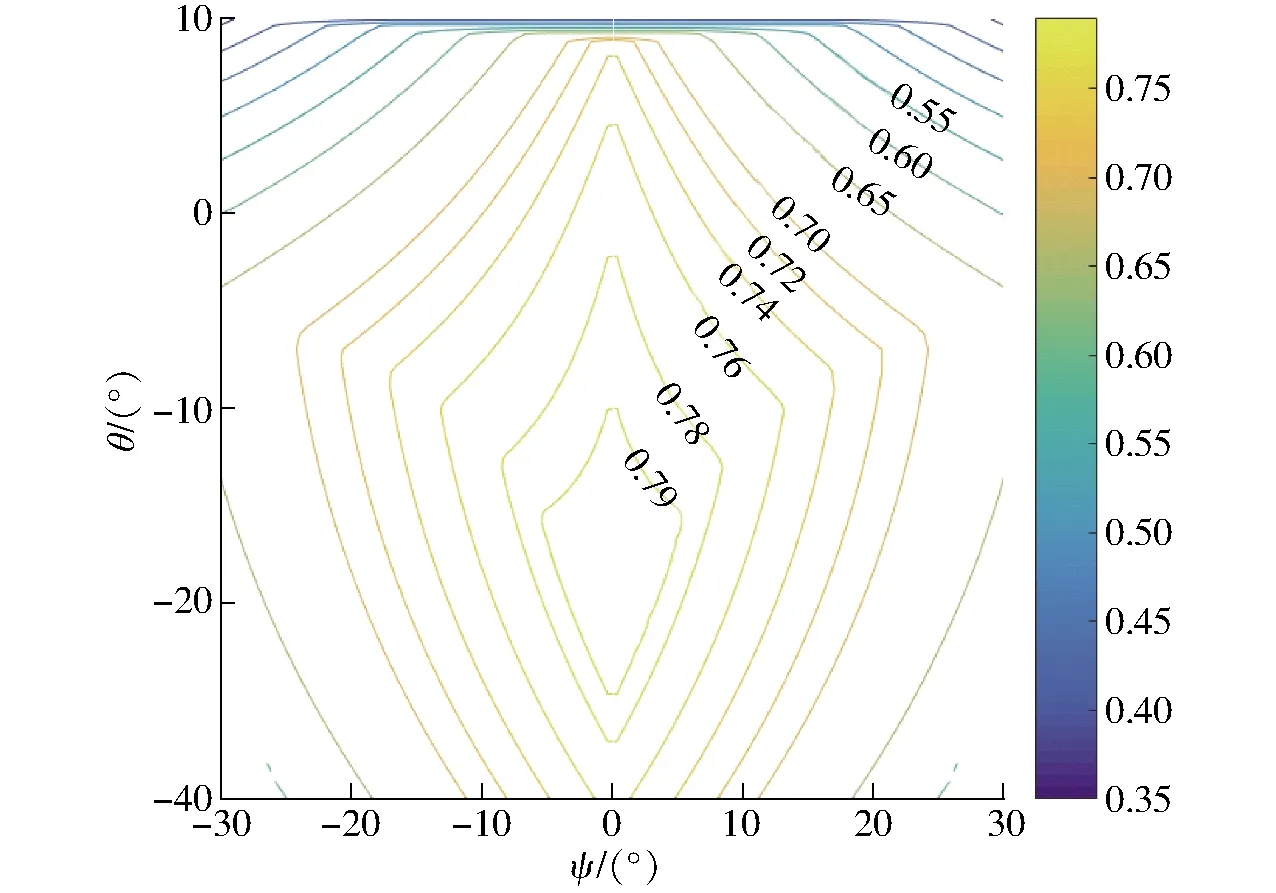
圖4 2-PUR-PSR并聯機構LTI在平面z=0.25 m內的LTI分布圖Fig.4 Distribution of LTI of 2-PUR-PSR parallel manipulator in plane z=0.25 m

圖5 2-PUR-PSR樣機Fig.5 Prototype of 2-PUR-PSR1.分支1(PUR) 2.驅動電機 3.分支2(PUR) 4.動平臺 5.分支3(PSR)

5 結論

(1)提出了基于極坐標方法的規則圓臺工作空間體積的計算方法，以2-PUR-PSR為研究對象，以規則工作圓臺空間體積和GTI為目標函數，以驅動限制和關節轉角限制為約束條件，以機構參數為設計變量，建立了2-PUR-PSR并聯機構尺度綜合多目標優化數學模型。

(2)基于MPSO算法得到了2-PUR-PSR并聯機構尺度綜合多目標優化的Pareto前沿，給出了18組Pareto最優解集，節約了設計時間。Pareto前沿的GTI最優值比優化前提高了57.57%，Vr最優值比優化前提高了37.59%，證明了優化方法的有效性。

(3)建立的2-PUR-PSR并聯機構的尺度綜合多目標優化模型也同樣適用于其他同類型的并聯機構。以機構在給定工作空間內具有優良的運動/力傳遞性能為目標，實現其尺度參數優選，可為后續機構剛度、運動學誤差、動力學等性能分析以及樣機制造奠定基礎。