2K-H 型行星齒輪裝置設計

張 展，武文輝

1上海電力環保設備總廠有限公司 上海 200072

2上海市機械工程學會 上海 200240

3中信重工機械股份有限公司 河南洛陽 471039

目前市場上見到的由錐齒輪組成的行星傳動大多是由外直齒錐齒輪組成，如汽車、工程機械上用的行星差速器，有 2 個自由度，用于運動的合成和分解。行星傳動的基本構件為太陽輪、內齒圈(或齒輪)和行星架(或轉臂、系桿)，若將其中某一構件加以固定，就成為 1 個自由度的行星齒輪傳動，常用的行星齒輪傳動以 2K-H 型居多[1]。

隨著科學技術的發展，加工手段不斷完善，CNC機床更新換代及配套 NC 模塊日益豐富，直齒或曲線齒的內齒錐齒輪也逐一研制出來，相關設計制造技術日趨完善[2-8]，于是便出現了由內齒錐齒輪嚙合的 2K-H 型行星齒輪傳動。筆者對由錐齒輪組成的2K-H 型行星齒輪裝置進行了簡述，給出了幾種基本類別的傳動比計算公式，并列舉總傳動比達 100 000以上的組合式錐齒輪行星傳動實例，進行了系統嚙合損耗和效率的評估。

1 2K-H 型行星傳動基本類別

1.1 按嚙合方式分類

行星齒輪傳動如圖1 所示。按行星輪系的基本構件組成來劃分，最常用的行星齒輪傳動型式為 2K-H型。GB/T 11366 標準規定 2K-H 型行星傳動機構定義為：由 2 個中心輪和 1 個行星架組成的行星齒輪傳動。2K-H 型行星齒輪傳動應用范圍廣闊，商用產品遍及各行各業。對于 2K-H 型行星齒輪傳動，還可按齒輪副嚙合方式的不同，細分成幾種基本類別。

圖1 行星齒輪傳動Fig.1 Planetary gear transmission device

錐齒輪行星傳動，筆者以字母 Z 來表示錐齒輪傳動(其他仍采用慣用表示法：N 為內嚙合，G 為共用行星輪，W 為外嚙合)，于是可以得到以嚙合方式特征符號標識命名的傳動類別。由錐齒輪組成的 2K-H型行星傳動有：ZNGW、ZNW、ZWW、ZNN 型，如圖2 所示；由圓柱齒輪組成的 2K-H 型行星傳動有NGW、NW、WW、NN 型，如圖3 所示。

圖2 由錐齒輪組成的 2K-H 型行星傳動Fig.2 2K-H planetary gear transmission composed of bevel gears

1.2 主要特點

錐齒輪 2K-H 型行星傳動的主要特點是：行星架H可與主軸線(即進、出軸的軸線)呈任意軸交角Σ輸出，可應用于多種使用場合，滿足各種使用需求。

ZNGW 型、ZNW 型適合廣闊功率范圍，功率區間基本不受限。ZNGW 型結構簡潔，傳動效率更高，實用功率范圍更大；ZNW 型則具有更大的傳動比區間，但其結構相對 ZNGW 型稍復雜些，制造難度亦較高。

圖3 由圓柱齒輪組成的 2K-H 型行星傳動Fig.3 2K-H planetary gear transmission composed of cylindrical gears

ZWW 型、ZNN 型適合很廣闊的傳動比范圍，但隨傳動比的增大，齒輪嚙合(無功)功率流變大，嚙合損耗顯著增加，機械傳動效率明顯下降。巨大的傳動比不適合用于功率型動力傳遞場合，宜用作超大傳動比的運動傳遞。ZNN 型的傳動比范圍更廣，最大可達到 10 000 左右，其對應效率很低，總嚙合效率在0.5% 以下。

2 2K-H 型行星傳動傳動比計算

由圖2 可知，當錐齒輪副軸交角Σ=0 時，就可演變成普通的圓柱齒輪傳動的 2K-H 型行星齒輪傳動，如圖3 所示。因此，錐齒輪傳動比的計算與普通圓柱齒輪傳動的 2K-H 型行星齒輪傳動相仿，則圖2所示的由錐齒輪組成的 2K-H 型行星傳動的傳動比可由圖3 所示機構的傳動比[9]引申得到。

圖2、3 中(a)、(b)、(c)3 種類型同標記構件的傳動關系完全相同，傳動比的計算表達式完全一致。圖2(d)、3(d)所示主從動a、b關系是倒置的，傳動比互為倒數。

由錐齒輪組成 2K-H 型行星傳動的傳動比計算公式如下：

(1)ZNGW 型傳動比

(2)ZNW 型傳動比

(3)ZWW 型傳動比

(4)ZNN 型的傳動比

3 行星齒輪傳動設計實例

傳動比為 262 500 行星齒輪傳動如圖4 所示。

圖4 傳動比為 262 500 行星齒輪傳動Fig.4 Planetary gear transmission with transmission ratio 262 500

3.1 傳動比

圖4 所示機構可以看成由z1、z2、z3、z4、H組成的 2K-H(ZWW)型和由z3、z4、z5、z6、H組成的2K-H(ZNN)型復合構成的組合輪系。

由a輸入、b輸出的傳動比

由z1、z2、z3、z4、H組成的行星輪系，轉化機構中H相對固定，輸出z4、輸入a上z1齒輪轉向相反，所以其傳動比

因此，可得輸入端a到行星架H的傳動比

由z3、z4、z5、z6、H組成的行星輪系，其轉化機構中z6和z4轉向相同，所以其傳動比

因此，

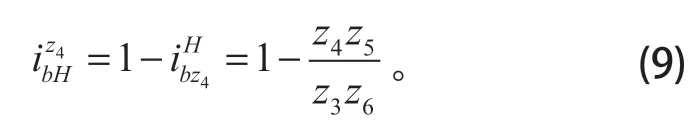
由此可得行星架H到輸出端b的傳動比

將式(7)、(10)代入式(5)，即得到圖4 傳動裝置的傳動比

將z1=12、z2=40、z3=40、z4=303、z5=33、z6=250 代入式(7)、(10)，即可求得組合機構各分部的傳動比

將以上結果代入式(5)，或將已知齒數直接代入式(11)即可得總傳動比

iab為正值，說明輸出與輸入同向旋轉。

3.2 傳動機構嚙合效率估算

若不計節軸處的機械損耗，輸入a、輸出b轉矩分別為Ta=T1、Tb=T6。

3.2.1 靜態平衡

(1)不考慮機械損耗，由輸入轉矩與總傳動比求得名義輸出轉矩

(2)由輸入轉矩與第一級齒數比求得z2齒輪轉矩

(3)從輸出端推算z5齒輪轉矩

(4)z3沿固定的z4被迫轉動，為被動輪，它所受轉矩為T5、T2之和

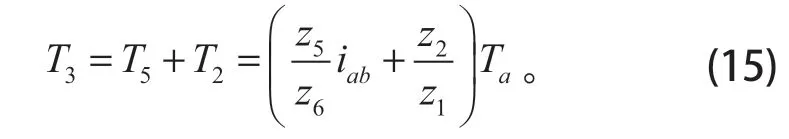
(5)固定齒輪z4所受力矩

將式(16)變形，結合式(11)、(12)可得

平衡條件：輸出、輸入實際轉向相同，對傳動裝置支座的作用轉矩為輸出、輸入轉矩之差。齒輪z4固定，圖4 的轉矩平衡條件可描述為T4=Tb-Ta。

由式(17)可知，在不考慮機械損耗時，齒輪所受的阻力矩等于輸出轉矩與輸入轉矩之差，系統外力矩處于平衡狀態。

3.2.2 嚙合功率損耗

采用超大傳動比時，總嚙合效率值η zΣ很小，Tb＜＜Tb0，Tb不能用輸入轉矩Ta與總傳動比的乘積簡單計算，需要建立方程求解。

不計具體損失值，功率以轉矩與轉速的乘積替代。

(1)齒輪的嚙合功率

嚙合功率是轉化(定軸)輪系中轉矩與轉速的乘積。轉化輪系中齒輪的轉速為齒輪絕對轉速與行星架轉速之差。齒輪z1、z2的嚙合功率

(2)嚙合損耗及系統嚙合效率

①齒輪z1、z2損耗

②齒輪z5、z6損耗

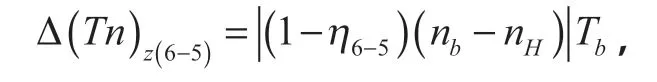
由于

所以

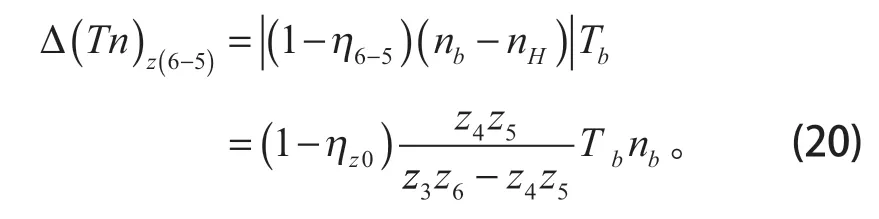
③齒輪z3、z4損耗

④嚙合總損耗及系統嚙合效率

齒輪z1～z6總嚙合損耗 Δ(Tn)z(1-6)為式(19)、(20)、(21)之和。

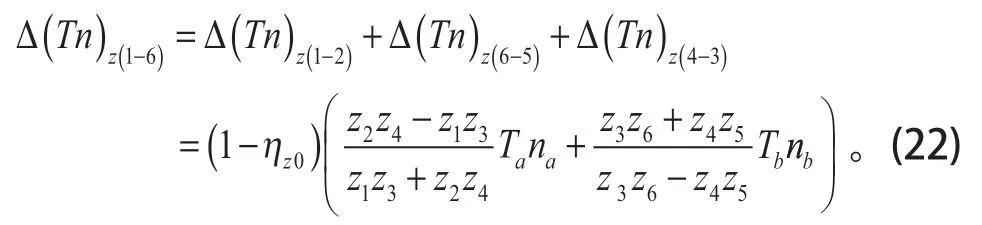
輸出功率方程

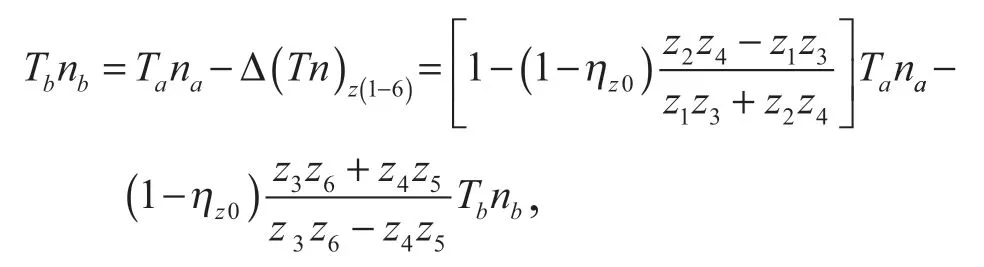
整理上式，得輸出功率

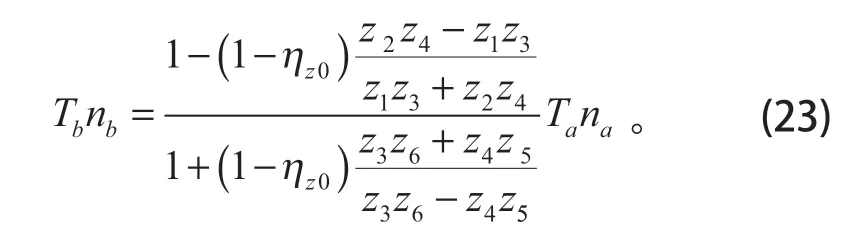
式(23)中Tana前面的乘項，即是系統的嚙合效率

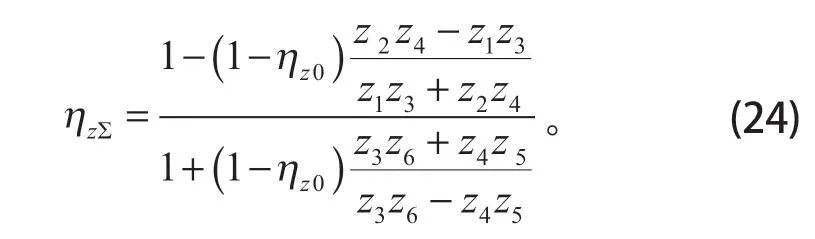
將各相關齒數代入上式，可得

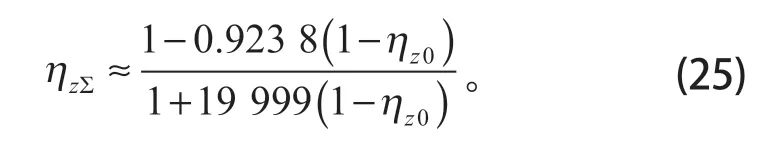
取ηz0=0.98，則

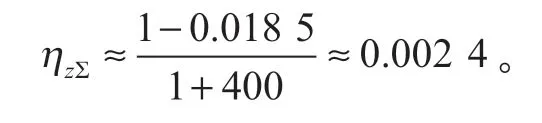
系統的嚙合傳動效率約為 0.002 4，輸出功率約為輸入功率的 0.24%，即額定輸出轉矩約能達到理想值的 1/500。

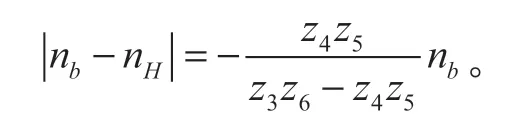
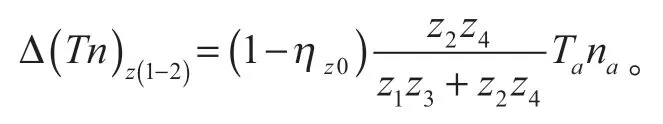
式(21)變為

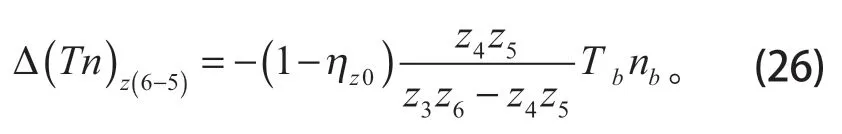
式(22)變為

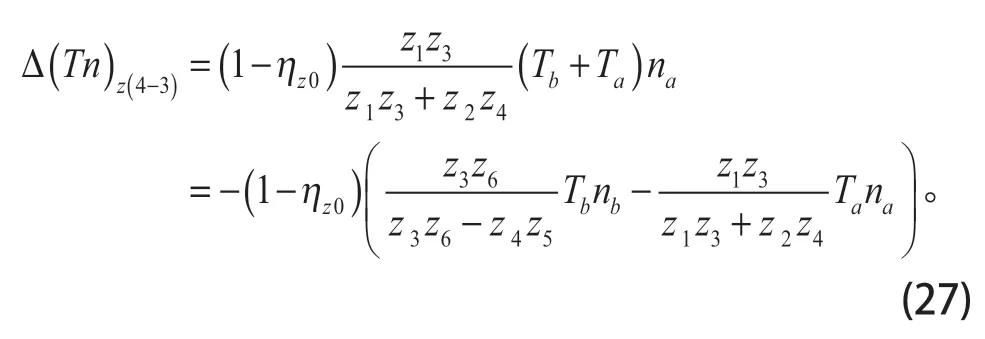
式(23)變為

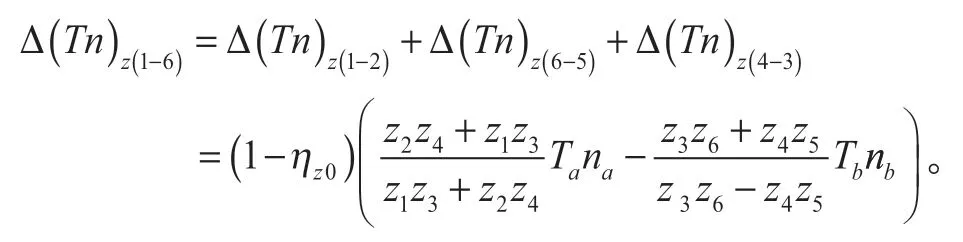
從而可推導出嚙合效率估算通式為

式中：“μ”處，“－”號用于輸入、輸出軸同向旋轉(z3z6＞z4z5)，“＋”號用于異向旋轉(z3z6＜z4z5)。

另外，傳動裝置中，軸承等受力運動組件的損耗，也應按輪系中的承載功率實況進行評估。一般來說，潤滑良好的軸承功率損耗要比齒輪的嚙合損耗小得多，每個滾動軸承的功率損耗可大致按軸功率的0.1% 粗略估算。

實際應用中，該類超大傳動比的傳動裝置，多以傳遞運動為首要目標。

4 結語

(1)錐齒輪組成的 2K-H 型行星齒輪裝置，行星架可與主軸線呈任意軸交角輸出，可適應各種使用需求。ZNGW 型、ZNW 型適合于大范圍功率的高效傳輸，ZWW 型、ZNN 型適用于大傳動比齒輪裝置。

(2)ZWW 型、ZNN 型錐齒輪行星傳動，可實現102～103量級的傳動比，但隨著傳動比的增大，內部封閉嚙合功率顯著上升，傳動效率近似呈反比式急劇下降，不適合中大功率的場合。

(3)錐齒輪組合型行星傳動，能實現 104～105量級的超大傳動比，可用于輸出轉動慢似時針的特殊場景；超大傳動比僅適用于不考慮機械傳動效率而單純以傳遞運動為首要目的的場合。