地球同步軌道衛星混合推進轉移軌道特性分析

段曉聞，祁瑞，* ，王敏

1. 北京理工大學 宇航學院，北京 100081 2. 中國空間技術研究院，北京 100094

燃料消耗是開展軌道轉移任務優化設計的重要約束。相比于傳統化學推進，電推進因其比沖高的特性，能夠大大降低燃料消耗，為任務提供更大的有效載荷[1-4]。然而，由于推力較小，電推進任務往往要求更長的轉移時間。如果將化學推進和電推進兩種方式結合，則有可能在減少燃料消耗的同時，加快軌道轉移時間，在燃料消耗和轉移時間之間達到折中。這種推進方式被稱為化學-電混合推進。采用混合推進，不僅拓寬了GEO任務設計的可行空間，也具有燃料消耗低、轉移時間短、發射窗口不敏感的優勢。在混合推進軌道的設計過程中，全電推進和全化學推進作為混合推進的特殊形式，為任務解算提供了可參考的邊界。

到目前為止，已經有學者在化學-電混合推進轉移軌道優化設計方面開展了研究，并做出了重要貢獻。1962年Edelbaum率先分析了混合推進的設計方法，此方法僅給出了初步的概念，并沒有對具體任務開展針對性分析[5]。隨后，Oleson等基于NASA Glan開發的SEPSPOT Sachett工具包開展了混合推進轉移設計[6]。Mailhe等改進了從近地軌道到地球同步赤道軌道的共面轉移方案[7]，整個過程先由電推進推離LEO，后到達某高度采用化學推進進行兩次霍曼轉移，最后經由電推進注入GEO。文中對整體輻射劑量的影響作了表征，并在系統層面對混合推進航天器任務進行了初步設計。Oh等設計了兩階段系統和三階段系統，但后續有學者指出其三階段的設計中沒有考慮電推進發動機工作后再施加脈沖推力的沖擊影響[8]。Kluever對GEO軌道轉移的化學-電混合推進方案進行了分析[9]，并開發了一種可以快速開展大推力和電推進軌道轉換權衡的算法[10]，文中將各種LEO-GEO的混合推進軌道轉移數據數值化，大大提高了解算速率。然而，該方法由于簡化條件太多，只適合軌道的初步設計。楊傅等采用高斯偽譜法對化-電混合推進展開研究，得到了一種快速解算算法[11]。Ceccherini和Topputo等在系列文章中創新地引入二維過渡軌道搜索網格解算混合推進軌道[12-15]，本文的相關研究就以此為基礎。

在混合推進軌道優化問題中，過渡軌道的確定是關鍵，從過渡軌道到目標軌道的小推力轉移段的設計優化是難點。本文以從近地軌道到地球同步軌道的混合推進轉移任務為背景，以Ceccherini和Topputo等開發的過渡軌道搜索網格算法模型為基礎，開展混合推進轉移軌道優化和分析。過渡軌道將整個GEO轉移軌道分為3部分：化學推進段、過渡軌道段以及電推進段，其中化學推進階段采用Lambert轉移方法解算，電推進階段采用混合法解算。

1 優化問題描述和模型介紹

在進行優化前，首先需要明確混合推進中化學推進和電推進兩者的開機序列。Oberth效應指出，在速度較高的地方進行化學推進軌道機動較為有利，即化學推進在中心天體附近應用效率較高，而電推進則在遠離中心天體的位置的應用效率較高[16]。另外，對于混合推進軌道轉移，先進行電推進后再進行化學推進會對衛星造成瞬時沖擊影響，嚴重者可能損壞太陽翼[12]。因此，在近地軌道首先開啟化學推進發動機，使衛星變軌進入軌道高度較高的過渡軌道，衛星在過渡軌道上進行調整，展開太陽翼，然后開啟電推進發動機完成剩余變軌任務。整個混合推進轉移軌道分為3段：化學推進轉移段、電推進轉移段以及連接兩者的過渡軌道段，如圖1所示。化學推進段的推力大，作用時間短，在本文中取最省燃料解；電推進段的推力小，耗時長，取時間最優解。

圖1 化學-電混合推進軌道示意Fig.1 Schematic diagram of combined chemical-electrical propulsion

在化學推進段，一般采用霍曼轉移能夠求解同平面共拱線兩軌道之間的轉移。本文考慮了軌道傾角差，即需求解異面軌道間的轉移問題，因此采用Lambert轉移方案，解算速度增量時使用Gooding的Lambert問題解[17-18]。給定初始軌道上衛星的位置，遍歷初始軌道等待時間和軌道轉移時間兩個參數，便可尋優得到最優脈沖轉移段。

在電推進轉移段，由于笛卡爾坐標系描述的衛星狀態矢量是快變量，而Kepler軌道六要素可能存在奇異問題，因此本文采用改進的春分點軌道要素(p,ex,ey,hx,hy,L)建立帶J2攝動項的電推進段的動力學方程[19]。基于龐特里亞金極大值原理，將最優控制問題轉化為兩點邊值問題，用混合法求解最省時間問題。

矩陣形式的動力學表達式為[20-21]：

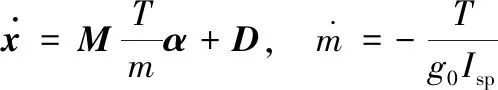
(1)

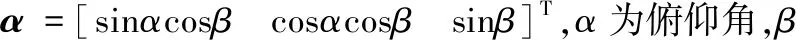
對應的Hamilton函數表示為：

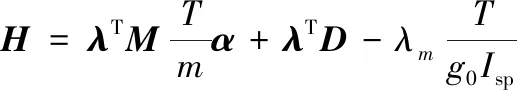
(2)

式中：λ=[λp,λex,λey,λhx,λhy,λL]T，為引入的改進春分點協態變量；λm為質量對應的協態變量。

最省時間問題可表述為如下兩點邊值問題：

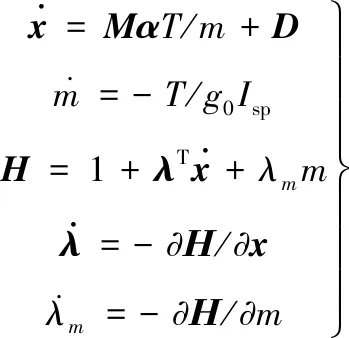
(3)

采用序列二次規劃和混合法進行優化解算。

本文中軌道優化任務的初始軌道為傾角28.5°、近地點高度200 km、遠地點高度2 000 km的橢圓軌道，默認其他軌道根數為零。目標軌道為GEO軌道。假設衛星的初始質量為1 500 kg，除軌道轉移外無質量損失。

2 解算模型

2.1 格點法

如果將過渡軌道參數(近地點距離、遠地點距離、軌道傾角)作為優化變量，與電推進段的協態變量一起優化，將導致優化變量多、算法難以收斂的問題。本文采用Ceccherini和Topputo等提出的格點法，將過渡軌道在搜索域內格點化，針對每條過渡軌道開展混合推進轉移軌道優化解算，然后在整個解空間中根據任務約束尋求最優解。

以近地點和遠地點距離表示的搜索網格如圖2所示，橫軸表示過渡軌道近地點距離Rp，縱軸表示過渡軌道遠地點距離Ra，第一象限內每一個“”符號代表一條過渡軌道。對于是否在網格劃分中考慮軌道傾角i和近地點幅角ω等變量，本文第2.3小節將開展討論。

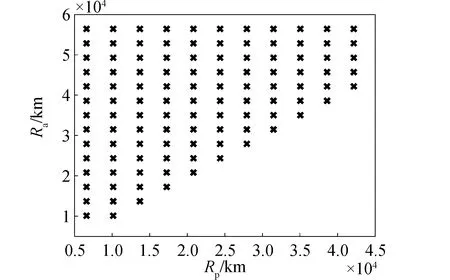
圖2 搜索網格示意Fig.2 Search grid diagram

2.2 邏輯構架

搜索網格中的每一個格點對應一條過渡軌道，順序求解化學推進段與電推進段，最后將結果整合形成完整混合推進轉移軌道。重復這一過程，直到遍歷采樣網格中的所有格點。解算流程如圖3所示[12-15]。

2.3 搜索網格簡化

第2.1小節的搜索網格示意中僅對近地點距離和遠地點距離進行了劃分，是否應當引入軌道傾角和近地點幅角這兩個維度，還需要進一步的分析討論。本節將對混合推進軌道優化設計中軌道傾角和近地點幅角變化帶來的影響進行分析，用以最終明確搜索網格中的優化變量。

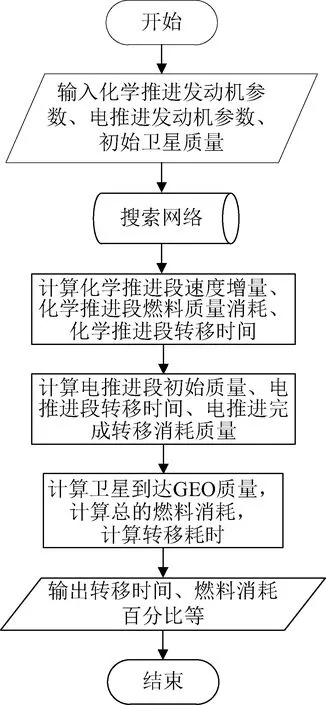
圖3 解算流程Fig.3 Solution flow chart

具體使用控制變量的方法，首先保持近地點幅角不變，令搜索網格中過渡軌道傾角變化，觀察其對整個混合推進軌道設計結果的影響；然后固定過渡軌道傾角，使近地點幅角變化，同樣觀察其對混合推進軌道的影響。

(1)軌道傾角變化對轉移軌道設計的影響

在下面的仿真中化學推進段取Isp1=300 s；電推進段Isp2=3 000 s，電推進發動機提供的推力為Tmax=0.2N；初始軌道取為近地點高度200 km、遠地點高度2 000 km的橢圓軌道，軌道傾角28.5°，近地點幅角取為0°，其他軌道要素皆假設為零。

由于初始軌道傾角為28.5°，目標GEO軌道傾角為0°，因此不同的過渡軌道傾角對應于化學推進段和電推進段對軌道傾角改變的不同貢獻。例如，當過渡軌道傾角為28.5°時，在化學推進段不進行軌道傾角調整，傾角調整完全由電推進段完成；當過渡軌道傾角為9.5°時，軌道傾角先由化學推進調整19°，再由電推進調整9.5°。圖4～圖8中標注的軌道高度為偏心率相同(e=1/11，Ra/Rp=6/5)，近地點半徑依次增大至GEO高度的一系列過渡橢圓軌道的近地點高度Rp。例如，x軸上近地點距離為10 000 km的點，表示近地點距離10 000 km，遠地點距離12 000 km的橢圓軌道。

由齊奧爾科夫斯基方程Δv=ve×ln(m0/mf)，速度增量與發動機有效排氣速度ve和燃料質量消耗m0/mf有關，而有效排氣速度可表示為ve=Ispg0。在本文中，脈沖段比沖與電推進段比沖是不同的，所以在燃料消耗問題中僅考察軌道轉移的總速度增量不夠嚴謹。本文將速度增量轉為始末質量比mGEO/m0能得出更直觀的結果，如圖4所示。總轉移時間Ttol隨過渡軌道傾角i和過渡軌道高度的變化曲線，如圖5所示。

圖4 始末質量比值隨過渡軌道傾角和 軌道高度的變化曲線Fig.4 The curve of beginning-to-end mass ratio with the inclination and the perigee altitude of searching orbit

圖5 總轉移時間隨過渡軌道傾角和 軌道高度的變化曲線Fig.5 The curve of transfer time with the inclination and the perigee altitude of searching orbit

圖4和圖5刻畫了過渡軌道高度和軌道傾角改變時衛星的始末質量比值和轉移時間的變化規律，其中m0為衛星在初始軌道的質量，mGEO為衛星到達GEO的質量。圖4中，縱軸為整個轉移過程末質量與初質量比值mGEO/m0。該比值較大時，說明軌道轉移消耗的燃料少，傳送至GEO的質量多；反之，說明軌道轉移消耗的燃料多。由圖4可見，實線最左端出現了最高的mGEO/m0值，該點表示衛星從初始軌道至GEO的整個轉移過程完全由電推進完成。另外，點劃線位于所有曲線最下方，表示僅采用化學推進進行傾角調整時消耗的燃料較多，也就說明采用電推進調整傾角在燃料消耗方面具有優勢。圖5中當過渡軌道傾角減小，電推進承擔的傾角改變量變小時，整個轉移過程耗時減小，這說明電推進段進行軌道平面的調整較為耗時。

可以看出，采用化學推進調整軌道傾角時，軌道轉移時間較短，但燃料消耗較多；采用電推進調整軌道傾角時，消耗的燃料較小，但轉移時間較長。由于過渡軌道傾角的不同取值，對混合推進轉移軌道燃料消耗和轉移時間的影響較大，故在本文的搜索網格構建中，加入了軌道傾角變量。

(2)近地點幅角變化對轉移軌道設計的影響

這里分析近地點幅角變化對轉移軌道設計的影響，在仿真中，選取的初始軌道為近地點高度200 km、遠地點高度2 000 km、軌道傾角28.5°、近地點幅角為120°的橢圓軌道，取Isp1=390 s；電推進段Isp2=3 000 s，Tmax=0.2 N。設定過渡軌道近遠地點距離與軌道傾角變化影響分析中相同。

化學推進段速度增量ΔVCP隨過渡軌道近地點幅角ω和過渡軌道高度的變化如圖6所示。圖6中的近地點幅角為過渡軌道的近地點幅角，由于初始軌道近地點幅角取為120°，因此不同曲線對應于化學推進段和電推進段對近地點幅角調整的不同貢獻。例如，當過渡軌道近地點幅角為120°時，在化學推進段不進行近地點幅角調整，其調整完全由電推進段完成；當過渡軌道近地點幅角為80°時，近地點幅角先由化學推進調整40°，再由電推進調整80°。

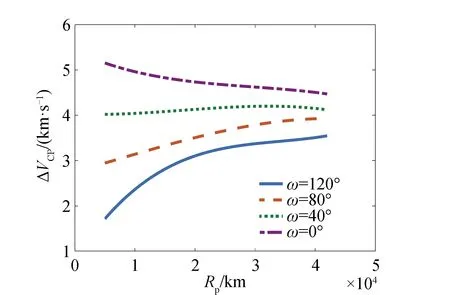
圖6 化學推進段速度增量隨過渡軌道近地點幅角和 軌道高度的變化曲線Fig.6 The variation of the velocity change in the chemical segment

由圖6可知，當軌道高度固定時，過渡軌道的近地點幅角越小，完成軌道轉移所需的速度增量越大。這說明，對于近地點幅角的調整，應當由電推進段來承擔完成，這樣較省燃料。

電推進段轉移時間TEP以及速度增量ΔVEP隨過渡軌道近地點幅角ω和過渡軌道高度的關系分別如圖7和圖8所示。

圖7 電推進段轉移時間隨過渡軌道近地點幅角和 軌道高度的變化曲線Fig.7 The variation of transfer time of electric segment

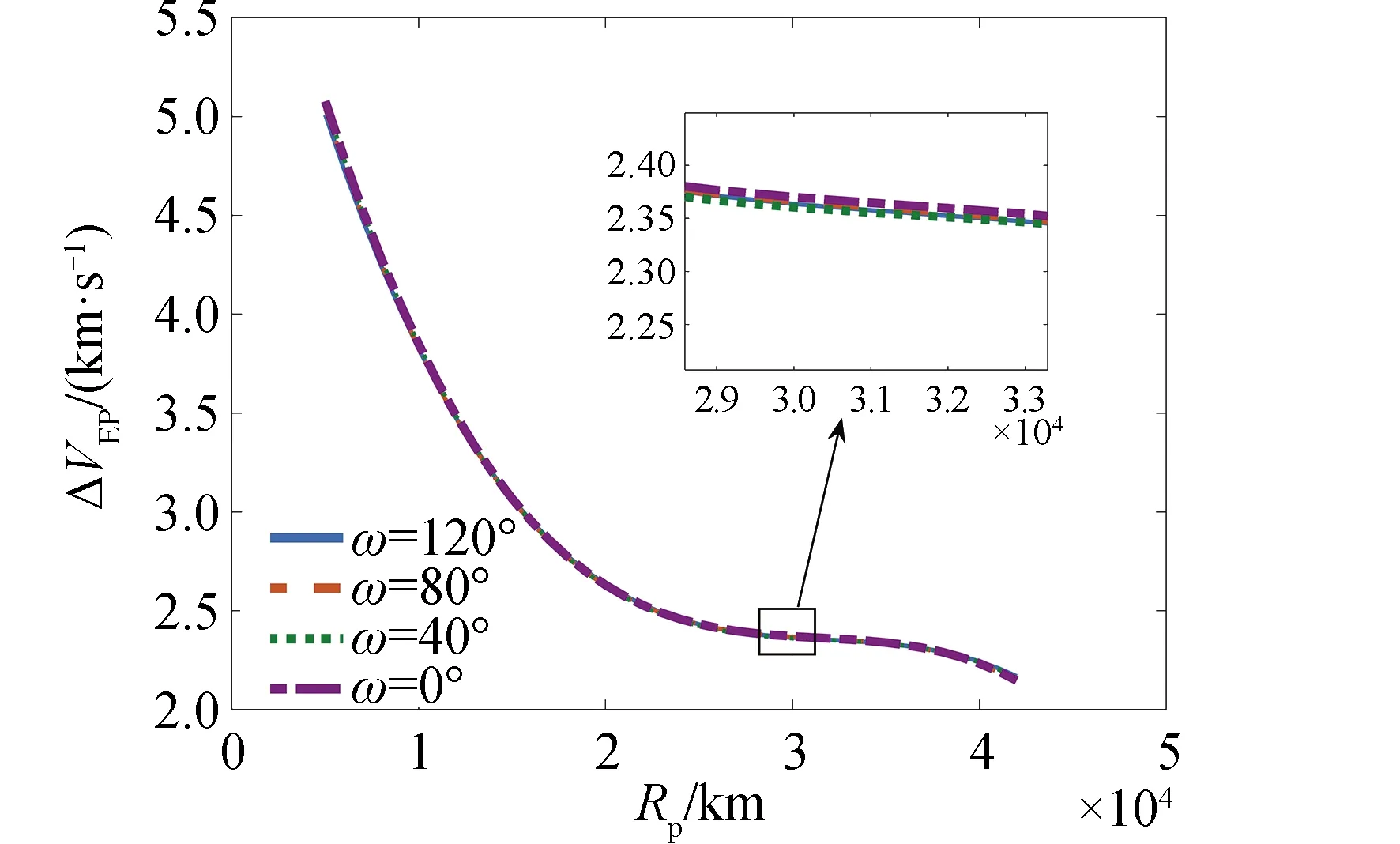
圖8 電推進段速度增量隨過渡軌道近地點幅角和 軌道高度的變化曲線Fig.8 The variation of velocity change of electric segment

由圖7和圖8可以看出，對于具有不同近地點幅角的過渡軌道，電推進段軌道轉移時間和速度增量的差別不大，說明過渡軌道近地點幅角的變化對電推進轉移過程的影響較小。

對圖6～圖8進行比較可以看出，相比于化學推進，采用電推進進行近地點幅角調整較為有利。因此，本文假定近地點幅角調整全部由電推進完成，故在搜索網格中不設置相應搜索變量。

(3)簡化后的搜索網格

最終簡化后的搜索網格包含過渡軌道近地點距離、遠地點距離和軌道傾角3個維度。以近地點高度Rp為x軸，遠地點高度Ra為y軸構建采樣網格，其中:

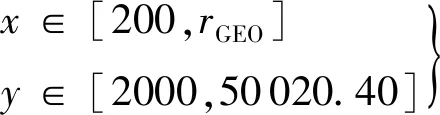
(4)

單位km，且滿足x≤y。在此范圍內平均取橫向格點數11，縱向格點數14，可以得到圖2所示的二維網格。在此基礎上，增加軌道傾角維度，軌道傾角i的變化范圍為：

i∈[0°,9.5°,19°,28.5°]T

(5)

加入了軌道傾角維度之后，搜索網格(見圖9)變為三維網格，格點區域覆蓋初始軌道至目標軌道之間的整個區域。依照流程(見圖3)進行解算，可以得到混合推進軌道在整個搜索域上的優化設計結果。

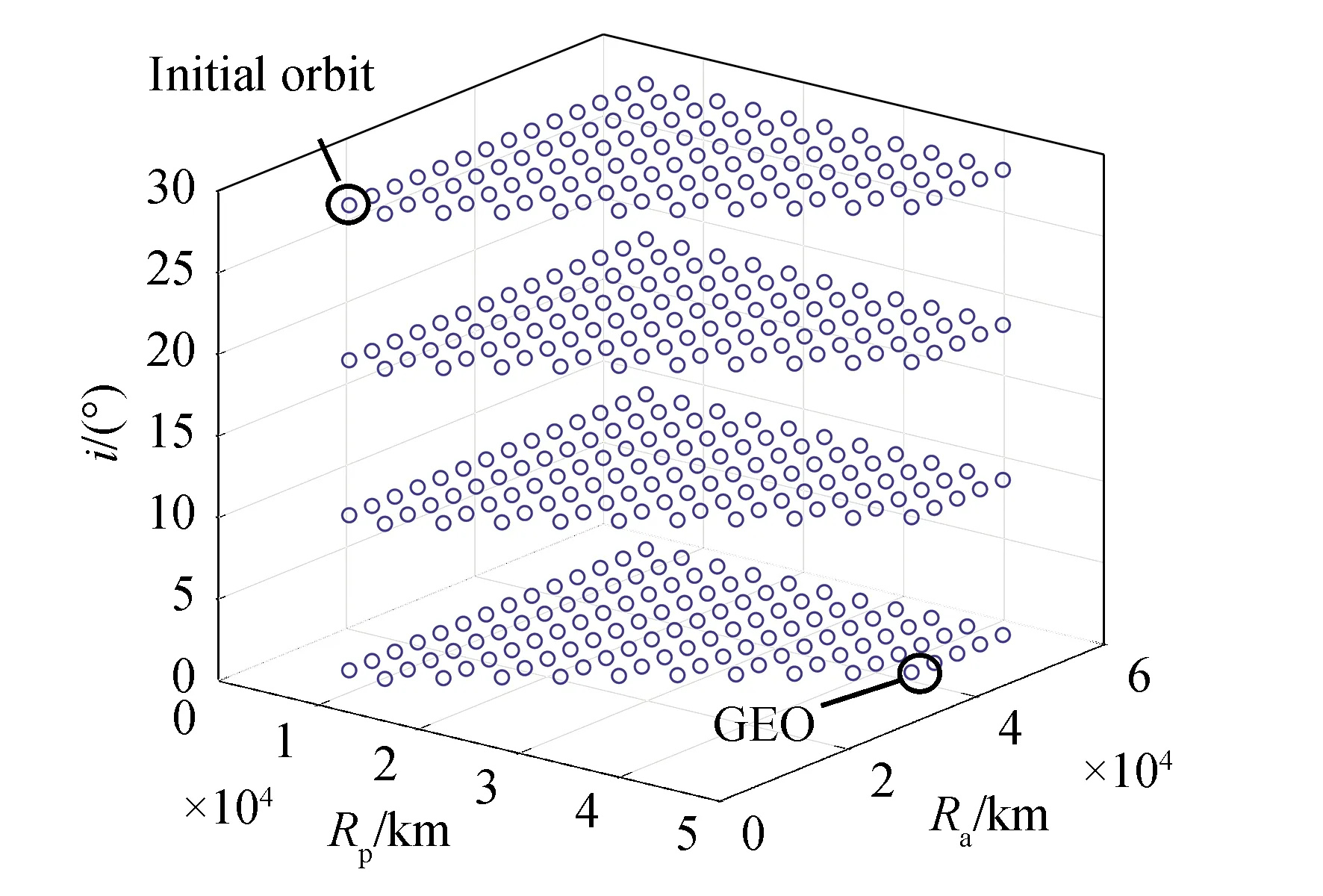
圖9 搜索網格Fig.9 Search grid

3 數值仿真結果

在由搜索網格界定的整個搜索域上，開展混合推進轉移軌道優化解算，仿真參數如表1所示。始末質量和轉移時間曲面分別如圖10和圖11所示。

圖10中展示了化學-電混合推進轉移中始末質量比值在搜索域上的變化規律。可以看到，過渡軌道傾角為28.5°時，對應的曲面位于所有曲面之上，即此時始末質量比值較大。這表示衛星從初始軌道轉移至GEO的整個過程中，軌道傾角調整完全由電推進完成，轉移的有效載荷最高。相反，過渡軌道傾角為0°的曲面，始終位于所有曲面最下方，說明完全使用化學推進將軌道傾角調整為0°對燃料的消耗最大。值得注意的是，在mGEO/m0比值為0.3～0.4范圍內，軌道傾角為9.5°、19°、28.5°三個曲面出現了重合或是相交的部分。結合圖11相同轉移軌道區域內的轉移時間可以看出，在某些情況下，采用化學推進分擔部分傾角的調整也是有意義的，能大大減少任務耗時。單就一個曲面而言，可以觀察到同一過渡軌道傾角條件下始末質量比值在搜索網格中的變化趨勢。可以看出，過渡軌道離初始軌道越遠，始末質量比值越小，衛星的質量傳送效率越低。

表1 仿真參數

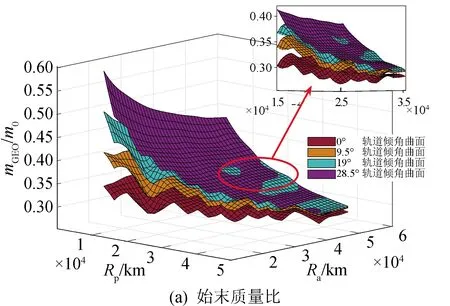
圖10 混合推進軌道設計始末質量比值mGEO/m0Fig.10 The beginning-to-end mass ratio mGEO/m0of the hybrid propulsion orbit design

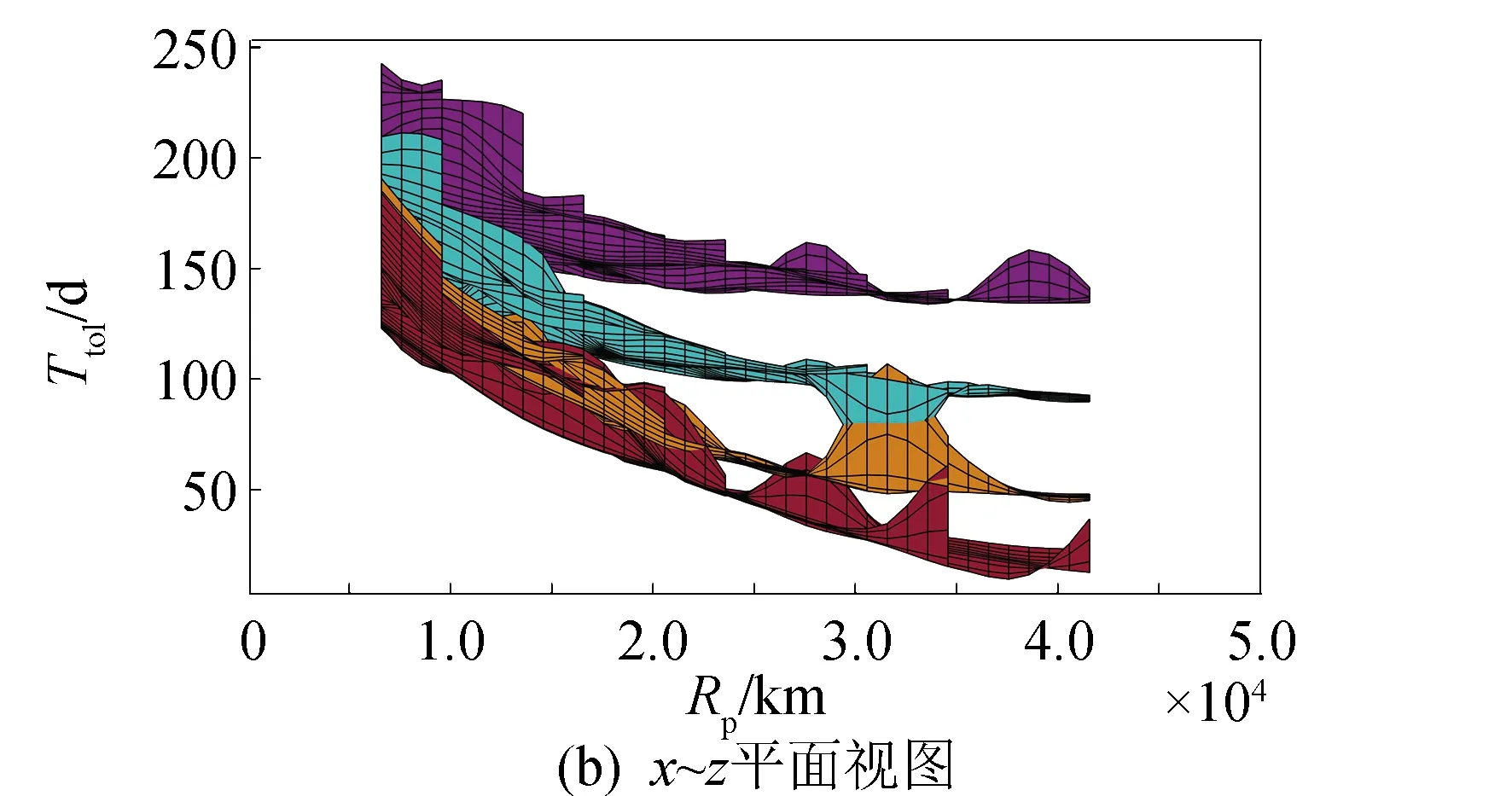
圖11 混合推進軌道設計轉移時間Fig.11 Transfer time chart of hybrid propulsion trajectory design

圖11中展示了混合推進轉移時間在整個搜索域內的變化規律。可以看到，過渡軌道傾角為28.5°時，對應的曲面位于所有曲面之上，這說明當軌道傾角完全是由電推進完成時，轉移耗時較長。同時也可以看出，若轉移完全由化學推進完成，則轉移時間最短。值得注意的是，在離初始軌道較近的區域(近地點距離[25 000～40 000]km)范圍內，曲面出現了重合或是相交的部分，結合圖10中相同區域內的始末質量比，說明可對該區域內的化學推進段做更有效的能耗優化，即在轉移時間相同時減少化學推進段對傾角調整的量，達到省燃料的目的。就其中一個曲面可以觀察到同一過渡軌道傾角條件下始末質量比值在搜索網格中的變化趨勢。值得注意的是，在近地點距離相同時，過渡軌道為大偏心率軌道時的轉移時間較小。

圖10和圖11提供的解算結果，可應用于實際任務軌道的選取。假設任務要求設計一條始末質量比0.55以上、轉移時間100～200 d的軌道。由圖10可以查出滿足始末質量比的過渡軌道范圍：傾角9.5°以上，近地點距離10 000 km附近。然后，在圖11中相應過渡軌道范圍內，選取時間最優解即可。

4 結束語

本文以地球同步軌道衛星化學-電混合推進轉移為任務背景，開展軌道優化設計與分析研究，以Ceccherini和Topputo等提出的過渡軌道搜索網格算法模型為基礎，增加了過渡軌道傾角維度，以轉移始末質量比和轉移時間為兩個指標，構建起包含化學推進段、過渡軌道段和電推進段的混合推進轉移軌道優化和分析方法。借助數值仿真，得出下列結論：

1)本文算法可以提供具有不同燃料消耗和轉移時間的混合推進轉移解集，相比于全化學推進和全電推進解，拓寬了解空間，方便軌道設計人員根據任務約束靈活選用。

2) 在混合推進軌道的優化中，過渡軌道近地點幅角的取值對電推進段軌道優化結果的影響不大，但對化學推進段的燃料消耗有顯著影響。

3)過渡軌道傾角的取值對混合推進轉移軌道燃料消耗和轉移時間的影響非常顯著，應當將其作為搜索網格中的一個維度，開展優化設計。