政府與科技型企業創新發展的演化博弈與仿真研究

何燕子，丁志鵬，郭柯楠

（1.湖南工業大學 商學院，湖南 株洲 412007；2.河南農業大學 信息與管理科學學院，河南 鄭州 450046）

0 引言

改革開放以來，我國經濟穩定上升，并保持著較高的速度向前發展。黨的十九大報告中指出，我國經濟正處在轉變發展方式、優化經濟結構、轉換增長動力的攻關期。

落后就要挨打，在科技強國的背景下，科技發展進程決定了國家的強弱，國家經濟的增長離不開科技創新，科技的創新發展是經濟增長的第一指標。在“十三五”期間，國家陸續出臺了有利于中小企業發展的相關政策，“在三去一降一補”中，對企業降負尤為突出。科技型企業本身具備一定的科技創新能力以及產品研發導向，因此，在減稅降負背景下，研究政府激勵與懲罰措施對科技型企業的創新發展影響，構建政府與企業的互利情形，保證科技型企業能夠在創新高質量發展的同時達到政府的滿意度，成為當前經濟發展階段必須要考慮的問題。實踐證明，技術創新能力是內生的，需要通過有組織的學習和產品開發實踐才能獲得[1]。由于科技創新需要前期成本投入以及存在失敗的風險，因此需要外部環境進行適度的引導，只有這樣才能保證其穩定發展。由此可見，研究政府與科技型企業創新發展之間的博弈關系具有重大意義。因此，本研究擬考慮企業的高效穩定創新發展，構建政府和科技型企業的演化博弈模型，并研究兩者在技術創新中的策略選擇。即首先，通過復制動態方程求出模型局部均衡點，然后對均衡點的穩定性進行分析，最后運用Matlab 軟件對政府和科技型企業的交互行為演化穩定趨勢進行數值仿真，以驗證所提模型的有效性，給出相應的政策建議，為我國經濟的高質量穩定發展提供理論依據。

1 研究綜述

1.1 創新

創新效率的概念最早是由S.N.Afriat[2]提出來的，創新效率主要是指創新活動的技術效率，即合理的投入產出比例。此后，K.Pavitt[3]的研究結果證明了研發與創新之間有著顯著的關系。C.Franco 等[4]研究了創新效率的主要影響因素，發現隨著時間的推移，放松監管能夠較大程度地提升研發效率。周姣等[5]、余珮等[6]、劉滿鳳等[7]均對我國高新區的創新效率進行了考察。在社會經濟高速增長的時代，省內部分區域創新效率高的企業能夠帶動其他效率低的企業。隨后，一些學者根據現有數據繼續深入研究，其中，范德成等[8]認為中國高技術產業技術創新實際效率整體處于中等水平，三大區域間、省際間均存在顯著的差異。

1.2 科技型企業

科技型企業也稱高技術企業，這些企業的發展與壯大源自于高新技術產業的發展，而高新技術的發展離不開企業的研發與創新。K.J.Arrow[9]、A.Q.Krueger[10]、P.M.Romer[11]、Z.ACS 等[12]均認為，政府財政科技支出能夠促進企業創新。錢麗等[13]認為，管理水平、區域創新生產技術不足影響了我國企業技術研發與成果轉化能力。張娜等[14]認為，研發經費的投入、國有產權的比例、外商直接投資等是影響我國高技術產業技術創新的重要因素。張永安等[15]研究發現，創新政策、政府項目、補助資金等都對企業的創新效率產生積極作用。杜楠等[16]研究認為，政府可通過發展戰略、稅收優惠政策等引導科技型中小企業的創新方向；此外，可通過資助、補貼等手段降低企業創新成本，提高企業的研發效率。戴浩等[17]認為政府補助能夠幫助科技型中小企業，通過技術創新實現企業成長，效果明顯，且需要進一步推行與完善引導政策。

1.3 博弈論演化理論

博弈論現已成為經濟學研究的重要工具。基于博弈論視角的探討主要分為政府與企業之間的博弈以及企業與企業之間的相互博弈。趙慧芳等[18]以靜態博弈模型分析了政府投資和企業投資間的博弈關系。李恩極等[19]認為，政府有必要對企業給予創新補貼，但補貼方法和效率有待改善。黎振強等[20]、李煜華等[21]分別構建了科技型企業合作創新的動態博弈模型，討論了企業合作創新的條件和動力機制。

2 模型假設與符號定義

國內外科研工作者關于政府與企業間的博弈關系研究也不少，但是針對政府與科技型企業創新發展之間的關系則少有探討，特別是關于政府與科技型企業間的演化機理及動態關聯少見報道。因此，本文擬對政府與科技型企業創新發展間的博弈關系進行分析。首先，基于博弈論演化理論，構建政府與科技型企業間的動態博弈模型，并加入政府上級第三方監督力量，合理構建科技型企業創新體系。然后，對構建的博弈模型進行仿真。在仿真分析方面，本文采用 Matlab 軟件，仿真分析各因素對博弈雙方行為的動態影響，探索科技型企業創新高效發展道路，為我國經濟高質量發展階段提供理論與實證依據。

作為利益相關者的“科技型企業”和“基層政府”，均期望通過不同策略的調整來獲得各自最大利益，因而雙方間存在著博弈關系。

假設1博弈雙方均為理性經濟人，企業策略集可選擇創新與不創新，基層政府的策略集可以選擇監管或者不監管行為，科技型企業的策略集可以選擇進行技術創新與不進行技術創新。

假設2基層政府根據科技型企業創新行為采取獎勵措施，觀察到科技型企業不創新進行處罰。

假設3基層政府監管的比例為x（0≤x≤1），不監管比例為（1-x）；科技型企業進行技術創新的概率為y（0≤y≤1），不進行技術創新的比例為（1-y）。

假設4基層政府進行監管，付出的監管成本為Ca，基層政府進行監管而獲得的相應社會收益為Ea，因此基層政府進行監管的收益為（Ea-Ca），若基層政府不進行監管，則收益為0。

假設5科技型企業不選擇技術創新的收益為Eb；選擇技術創新付出的成本為Cb，其中技術創新付出的成本包括創新人才的培養，以及購買高端先進設備等。因此，科技型企業選擇技術創新獲得的收益為（Eb-Cb）。

假設6科技型企業進行技術創新的主動性不強，管理層下達技術創新的決策會增加企業的額外運營成本。因此，基層政府需要對實施技術創新決策的科技型企業給予補貼或者對不進行技術創新性行為的科技型企業給予懲罰。

因此，本研究以基層政府懲罰科技型企業不進行技術創新為方向。即基層政府監管且發現科技型企業不進行技術創新，假設基層政府有a（0≤a≤1）[22]比例檢查到科技型企業不進行技術創新，對其懲罰金額為R1，則政府的收益為（Ea-Ca+aR1），科技型企業的收益為（Eb-aR1）。

假設7基層政府不監管，科技型企業不進行技術創新，不作為的基層政府會受到上級政府的處罰，聲譽損失為D，此時政府的收益為-D。

3 演化模型構建

根據前文假設，建立如表1所示基層政府與科技型企業演化博弈收益矩陣。

表1 基層政府與科技型企業演化博弈的收益矩陣Table 1 Income matrix of the evolutionary game between local governments and technology-oriented enterprises

3.1 基層政府與科技型企業的演化博弈分析

3.1.1 基層政府的演化博弈復制動態方程

假設基層政府群體中選擇監管的概率為x，則基層政府收益矩陣為

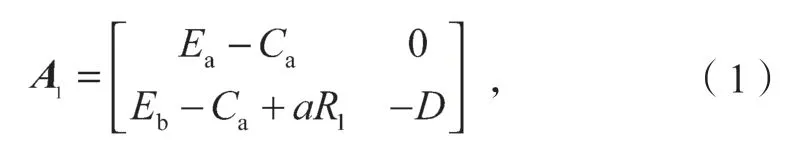
故可得基層政府進行或不進行監管的期望收益E1、E2及政府平均收益分別如下：

根據Malthusian 動態方程[23]，基層政府選擇監管的復制動態過程為：

3.1.2 科技型企業的演化博弈復制動態方程

假設科技型企業中選擇技術創新的概率為y，則科技型企業收益矩陣為

則科技型企業進行技術創新收益的期望E3、不進行技術創新收益的期望E4，以及平均收益的期望可分別表示如下：

同樣，參考文獻[23]，可得科技型企業選擇技術創新的復制動態過程為

令F(x)=0、F(y)=0，可得系統演化的5 個均衡點：（0,0）（0,1）（1,0）（1,1）（x*,y*）。其中：

根據演化博弈原理，5 個均衡點的局部穩定性可以由該系統相應的雅可比矩陣J的行列式detJ和跡trJ的值判定[24]。即當且僅當detJ＞0、trJ＜0 時，均衡點具有穩定性。

根據式（5）和式（10），可以得出系統的雅可比矩陣J為

其中，p11、p12、p21、p22分別如下：

矩陣J的行列式為，

矩陣J的跡為p11+p12。

代入均衡點（x,y）的值，得到各均衡點的雅可比行列式和跡的值，見表2。

表2 均衡點對應的雅可比矩陣行列式和跡的值Table 2 expressions of determinant and trace of jacobian matrix corresponding to equilibrium points

因均衡點（x*,y*）的跡的值為0，不滿足條件trJ＜0，因此（x*,y*）不是進化穩定策略（evolutionarily stable strategy，ESS）。表3給出了4 個均衡點為局部穩定點的條件。

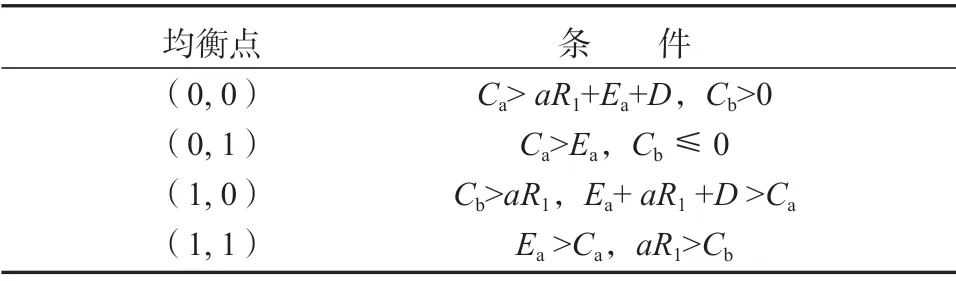
表3 各個均衡點成為局部穩定點的條件Table 3 Conditions for each equilibrium point to be a locally stable point

3.2 均衡點穩定性分析

3.2.1 點（0,0）

對于點（0,0），即（基層政府不監管，科技型企業不進行技術創新），當Ca＞aR1+Ea+D且Cb＞0時，其為唯一穩定點。該情況出現在基層政府監管初期和科技型企業進行技術創新發展階段。一方面，政府需要支付過多的人力進行監管，獲得的社會收益Ea較少，監管懲罰力度不夠，帶來的收益aR1較少，以及來自上級政府的懲罰D較小，容易出現Ca＞aR1+Ea+D；另一方面，受技術或設備方面的限制，科技型企業進行技術創新成本較大。從而形成（0,0）即（基層政府不監管，科技型企業不進行技術創新）的局面。

顯然，點（0,0），即（基層政府不監管，科技型企業不進行技術創新）不是創新高質量社會期望狀態。為打破這種均衡，需減少Cb，增大aR1、Ea、D。現實中，不僅需加強對科技型企業進行技術創新時所需人才的培養和設備的研發，以降低技術創新成本Cb；而且基層政府需加大對不進行技術創新企業的懲罰力度aR1，并加大對科技型企業技術創新的扶持以及獎勵，上級政府需要對基層政府宣傳創新，并且對高質量創新的管理進行正向引導，加大對其不作為行為的批評教育，提高聲譽損失D。

3.2.2 點（0,1）

對于點（0,1），即（基層政府不監管，科技型企業進行技術創新），當Ca＞Ea且Cb≤0 時，點（0,1）為唯一穩定點。這顯然是社會創新高質量發展最為理想的情況。然而現實社會中，這是不可能出現的。因為基層政府不監管及科技型企業進行技術創新的成本為0 的情況在現實環境中不存在。這是因為，科技型企業進行創新負責研發投入的成本不可能為0，所以這種理想狀態的均衡將會向點（0,0）即（基層政府不監管，科技型企業不進行技術創新）的方向傾斜。所以點（0,1），即（基層政府不監管，科技型企業進行技術創新）雖然是一種理想狀態下的均衡，但不符合社會發展實情。

3.2.3 點（1,0）

對于點（1,0），即（基層政府監管，科技型企業不進行技術創新），當Cb＞aR1且Ea+aR1+D＞Ca時，點（1,0）為唯一穩定點。這種情況一般出現在政府對于創新高質量發展的關注期。一方面，科技型企業進行技術創新的成本Cb依舊過高，科技型企業為了追求利潤依然自行其是；另一方面，上層政府督促基層政府以及監管帶來的社會收益（Ea值較為合適），能夠滿足Ea+aR1+D＞Ca，但是基層政府對不進行技術創新的科技型企業懲罰力度仍過小（aR1），易使Cb＞aR1。形成點（1,0），即（基層政府不監管，科技型企業不進行技術創新）的局面。

該情況也不是社會創新高質量發展的期望狀態，為打破這種均衡，需繼續增大aR1，降低Cb。即基層政府需繼續增大懲戒力度（F），并推動合格技術設備的生產研發（降低Cb）。

3.2.4 點（1,1）

對于點（1,1），即（基層政府監管，科技型企業進行技術創新），當Ea＞Ca且aR1＞Cb時，點（1,1）為唯一穩定點。這種情況一般出現在創新發展規范期，企業進行技術創新所需要的人才培養成本以及設備研發成本較小（Ea值較小），創新發展趨勢越來越被大眾重視（企業同行競爭較大），基層政府也有一個完備合理的懲罰機制（aR1值較為合理），上級政府對基層政府不作為的教育較嚴厲（D值較大），可以達成Ea＞Ca且aR1＞Cb的條件。此時，肯定社會創新發展是政府與科技型企業共贏的期望局面。

4 演化仿真分析

為進一步探究科技型企業與基層政府間的演化博弈關系，探討兩者達到演化均衡狀態的條件，用Matlab 軟件對上述情況進行仿真分析。

由博弈分析可知，當Ea＞Ca且aR1＞Cb時，系統會向期望均衡點（1,1）演化。設定滿足條件Ea＞Ca且aR1＞Cb的參數值Ca=4，a=0.4，R1=2，Ea=6，D=1，Cb=0.1，對x、y的初始值為（0.3,0.7）（0.8,0.2）進行仿真，得到圖1所示演化結果。由圖1可知，設定條件下，無論x、y的初始值如何選取，系統都會向點（1，1），即（基層政府監管，科技型企業進行技術創新）的期望方向演化。接下來以圖1的初始參數為基準，設定x=0.5、y=0.5，討論Ca、R1、D、Cb、Ea對演化結果的影響。

圖1 滿足Ea＞Ca，aR1＞Cb 時系統的演化結果Fig.1 Evolution results of the system with Ea＞Ca，aR1＞Cb

4.1 基層政府監管成本Ca 對演化結果的影響

設定Ca為1,3,5，對基層政府和科技型企業的策略演化進行仿真，結果見圖2。

圖2 Ca=1、Ca=3、Ca=5 時的系統策略演化結果Fig.2 Results of the strategy evolution of the system with Ca=1、Ca=3、Ca=5

對比分析圖中曲線可知，基層政府監管成本Ca值越小，基層政府收斂于嚴格監督策略和科技型企業進行技術創新的速度越快。其中基層政府對Ca值的變化非常敏感，科技型企業次之，均有明顯變化。這一結果表明，降低Ca值即降低政府監管成本將有利于社會創新高質量發展，因而有利于社會創新高質量發展局面的達成。

4.2 基層政府對科技型企業不進行技術創新的處罰R1 對演化結果的影響

設定R1=2、R1=4、R1=6，對基層政府和科技型企業的策略演化進行仿真，結果見圖3。

圖3 R1=2、R1=4、R1=6 時的系統策略演化結果Fig.3 Results of the strategy evolution of the system with R1=2、R1=4、R1=6

由圖3可以得知，相較而言，基層政府對R1值反應不敏感，而科技型企業對其敏感。可見，現實社會中，適當設置較高的罰金將有利于社會創新高質量發展的局面，并且科技型企業會更加積極推動社會高質量發展的進程。

4.3 基層政府放松監管時的聲譽損失D 對演化結果的影響

設定D=1、D=3、D=5，對基層政府和科技型企業的策略演化進行仿真，結果見圖4。

圖4 D=1、D=3、D=5 時的系統策略演化結果Fig.4 Results of the Strategy evolution of the system with D=1、D=3、D=5

由圖4可知，基層政府放松監管時受到上級政府批評的聲譽損失D值越大，基層政府策略收斂于嚴格監督的速度越快，而科技型企業變化不顯著。因此可預見在社會創新高質量發展體系中，創新水平高低與基層政府政績考核掛鉤，將有利于創新發展，且基層政府會更積極地推動社會創新高質量發展進程。

4.4 科技型企業進行技術創新的成本Cb 對演化結果的影響

設定Cb=0.1、Cb=0.3、Cb=0.5，對基層政府和科技型企業的策略演化進行仿真，結果見圖5。

圖5 Cb=0.1、Cb=0.3、Cb=0.5 時的系統策略演化結果Fig.5 Results of the strategy evolution of the system with Cb=0.1、Cb=0.3、Cb=0.5

對比圖5中曲線，可得知基層政府對Cb的變化反應不敏感，達均衡所需時間無明顯變化；但科技型企業對Cb的變化反應顯著，歷時明顯加快。可見，現實社會中，降低創新成本將使得科技型企業更傾向于選擇創新發展。

4.5 政府獲得社會收益Ea 對演化結果的影響

設定Ea分別為6,7,8，對基層政府和科技型企業的策略演化進行仿真，結果見圖6。

圖6 Ea=6、Ea=7、Ea=8 時的系統策略演化結果Fig.6 Results of the strategy evolution of the system with Ea=6、Ea=7、Ea=8

由圖6可以得知，基層政府所獲得的Ea值越大，其收斂于嚴格監管的速度越快，而科技型企業的變化不明顯。因此，加大政府的社會收益，比如說技術突破后的區域GDP 總值的提高、稅收的提高等，這將有利于基層政府推進創新高質量發展進程。

4.6 研究結論

經過以上分析，可得出以下結論：

1）當滿足Ea＞Ca且aR1＞Cb時，系統會向期望均衡點（1,1），即（基層政府監管，科技型企業進行技術創新）的方向演化。

2）滿足上述條件的同時，當基層政府付出的監管成本小于獲得的社會收益時，且基層政府進行監管獲得的社會收益越多，基層政府越傾向于嚴格監管，這時雙方達到演化平衡點的時間越短。若基層政府受到上級政府的批評督促越多，則基層政府傾向于嚴格監管的力度越大，博弈雙方達到演化平衡點的時間越短。

3）對于科技型企業，降低技術創新成本、增加基層政府對科技型企業不創新的罰金，均有利于科技型企業加快演化速度。

5 政策建議

從以上結論可知，基層政府和科技型企業能夠朝著互相共贏的期望局面發展，但是需要合理把控好兩者之間的利益關系。因此，如何構建基層政府和科技型企業之間的橋梁是促進社會進步、推進全面高質量發展的關鍵因素。

1）提升基層政府的監管能力，完善懲罰制度。首先，應加強基層政府的監管力度，把握好懲罰尺度以及金額，合理引導科技型企業走向技術創新道路。基層政府的監管能力高低決定了雙方演化博弈的穩定性，因此基層政府要充分發揮引領作用，具體為基層政府下設執法部門應該進行相關培訓，提高執法能力。監管科技型企業創新的同時，自身也需要不斷創新。其次，應建立合理的獎勵措施和對應的懲罰措施。對于科技型企業創新前期給予相應補助，扶持科技型企業渡過資金難關。

2）將地區技術創新程度劃入基層政府績效考核指標。一方面，上級政府應當引導基層政府構建合理的政企關系，對其進行指導和督促；另一方面，將地區科技型企業創新程度作為考核指標，從而嚴格要求基層政府。通過對基層政府的創新績效進行嚴格審查，包括懲罰獎勵措施和補償方案等[25-26]，促使基層政府達到上級政府要求的同時保證地區科技型企業的創新發展。

3）政府激勵科技型企業的技術創新主動性。科技型企業能否主動進行技術創新取決于技術創新帶來的收益高低，因此，基層政府應當做好相應的鼓勵以及獎勵工作，通過降低科技型企業創新成本來促進科技型企業進行創新活動。首先，政府可與高校建立合作關系，定向培養一大批科技型人才，提高創新的可能性。其次，引入大批先進設備，保證技術同步。最后，頒布相關法律法規，對于科技型企業創新的優惠政策提供法律保障，提高科技型企業創新的主動性。

4）合作共贏，提高創新效率，縮減創新成本。因為科技型企業進行技術創新需要前期投入大量成本，所以科技型企業進行技術創新不僅需要考慮政府與企業的關系，更要注重相關科技型企業之間的關系。一個地區內存在多家科技型企業，多方合作共享研究進展可以節省大批資金和時間。政府不僅需要搭建政企關系，同樣需要關注企業與企業之間的關系。通過建立多方共享平臺，可以實現技術共享、信息共享、資源共享等。這將大大提高創新效率，加快科技型企業技術創新的步伐。