坐標平面上的二重積分的數值算法

何洪英，張世

(西華師范大學，四川南充 637000)

積分算式決定于積分區域，幾個世紀以來，由于沒有重積分的數值算法，文獻和教材中二重積分的積分區域都相當簡單，用極坐標表示的積分區域常常只限于圓，所以本文作了較為詳細的介紹.

1 坐標平面上的二重積分算式和通用數值計算公式

坐標平面分為xOy平面，yOz平面，zOx平面和rOθ平面，這里只介紹xOy平面和rOθ平面，且只介紹xOy平面和rOθ平面上的積分并將其簡稱為二重積分.

xOy平面和rOθ平面上的二重積分的一般算式為：

(1)

(2)

(3)

二重積分與積分變量名無關，所以只須考慮式(1)和式(3).

能找到理論解的定積分不多.能找到理論解的二重積分更少，而且沒有通用算法，無法用計算機計算.

定理1當h1=(x2-x1)/n1→0，h2=(g2(x)-g1(x))/n2→0時，

(4)

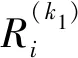
證明：二重積分理論解的確定過程為，先將外層積分變量視作常量對內層積分積分，將結果作為新的被積函數對外層積分變量積分.

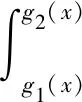
式中當k2為偶數時v=2，為奇數時v=1.

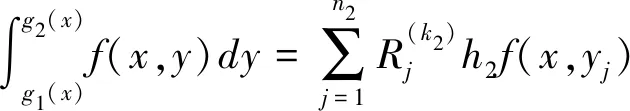
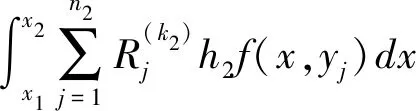
若用復合牛頓積分公式積分，當k1為奇數時v=1,為偶數時v=2.

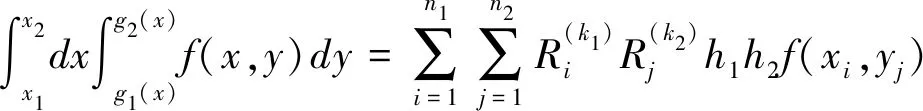
證畢.

(5)

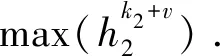
定理2 當h1=(r2-r1)/n1→0，h2=(g2(r)-g1(r))/n2→0時，若用復合牛頓積分公式計算，則

(6)

式(4)與被積函數無關，令f*(x,y)=xf(x,y)，則有

若用復合高斯積分公式，則有

高斯積分公式中高斯點與所選正交多項式不同而不同，本文只用高斯——勒讓德積分，即只選勒讓德正交多項式.

欲行積分須先有算式，二重積分算式由被積函數和外層積分上、下限(外層積分變量所取最大值和最小值)及內層積分的上、下限函數組成.式(1)和式(3)與被積函數無關，而且被積函數是用戶給定的，所以不……