用不同的數(shù)學方法解決同一個物理問題

圣寶建

摘 要：數(shù)學在物理學中的應用是非常廣泛的，使得物理需要依附數(shù)學而得以發(fā)展。有時候，人們可以借助數(shù)學方法來將一些較為復雜的物理問題轉(zhuǎn)化為較為簡單的數(shù)學問題。筆者介紹了利用數(shù)學里的導數(shù)思想求一元函數(shù)的最值和三元平均值不等式求最值的方法定理，并利用這兩種不同的數(shù)學方法巧妙地解決了物理學靜電場中的“等量的兩個同種正電荷連線中垂線上最大電場強度”的問題。

關鍵詞：數(shù)學;最大電場強度;導數(shù);三元平均值不等式

中圖分類號：G712 文獻標識碼：A

Abstract：The extensive application of modern mathematics in physics makes physics develop depending on mathematics.Sometimes，people can use mathematical methods to transform some more complex physical problems into simpler mathematical problems.In this paper，the author introduces how to use the idea of derivative to find the inequality of the maximum value and the mean value inequality of three variables in mathematics，and how to use these two different methods to ingeniously transform the "maximum electric field intensity problem on the vertical line of two equal positive charge lines" in physics electrostatic field into the problem of finding the maximum value of the function in mathematics.

Key words：mathematics;maximum electric intensity;derivative;mean value inequality of three variables in mathematics

偉大的數(shù)學家拉格朗日曾經(jīng)說過，他不用畫一張圖，就可以用數(shù)學分析的方法來解決力學中所有的問題。由此可見，這兩門學科之間關系密切。筆者利用導數(shù)和三元平均值不等式這兩種不同的方法巧妙地將物理學靜電場中“等量的兩個同種電荷連線中垂線上最大電場強度的問題”轉(zhuǎn)化為數(shù)學里求一元連續(xù)函數(shù)在開區(qū)間內(nèi)的最大值問題，并得到了相同的結果。

1 問題的提出

物理學中的電場強度是一個既有大小又有方向的矢量，單個的點電荷在真空中的電場的計算，直接套用電場強度的決定式[1]公式即可，而在空間中同時存在多個（本文只討論兩個）點電荷，這時在空間某點產(chǎn)生的電場強度便是兩個點電荷共同作用的結果，考慮到電場強度的矢量性，我們可以用數(shù)學里矢量的疊加法則—平行四邊形法則來解決，所以，P點的電場強度應該等于兩個點電荷各自在P點產(chǎn)生的電場強度的矢量和。為了描述方便，本文只介紹電荷量相等的兩個正電荷（負電荷類似）共同作用在P點時的電場強度的最大值問題[2]的兩種不同的數(shù)學求解方法。

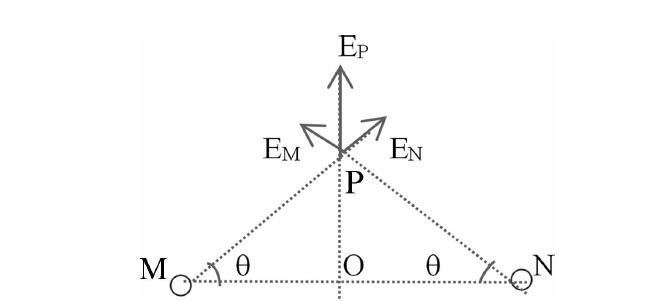
假設點P位于兩個帶有等量的同種正電荷的點電荷M、N連線的垂直平分線上（如下圖），如下圖所示，求M和N在P點處共同產(chǎn)生的最大電場強度（可以簡稱場強）。

我們知道，正電荷M和N各自在它們連線的中點O處會產(chǎn)生大小相等但方向相反的電場強度，所以，當P點恰好位于O點時，此時M和N在P點處產(chǎn)生的電場強度為零，是個定值，沒必要討論。下面我們探討P點不在O點時的情況。由于同種電性的電荷相互排斥，所以O點處附近的電場線非常稀疏，但電場強度并不為零，考慮到在等量的同種正電荷M和N的連線的垂直平分線上，從O點到無窮遠處，電場線是先變得密集后變得稀疏，那么電場強度是先變強再變?nèi)醯模瑥亩妶鰪姸鹊淖畲笾凳强陀^存在的，筆者在下文中給出了兩種不同的數(shù)學求解方法。

2 預備知識

2.1 真空中的點電荷形成的場強E的計算公式[3]

2.2 極值的判定定理[4]

2.3 最值的判定定理[4]

2.4 三元平均值不等式[5][6]

3 問題的兩種數(shù)學解決方法

由物理對稱性可知，在兩個電性相同、電量相等的點電荷的連線的中點處的電場強度為零，且P點的合場強是沿著中垂線遠離場源電荷且方向是豎直向上和豎直向下的，因為上下對稱，所以豎直向上的合場強和豎直向下的合場強是等大的，故只需考慮豎直向上的情況即可。而由預備知識可知，在中垂線上距離O點無窮遠處的電場強度大小也為零，所以，由公式（1）及矢量合成的平行四邊形法則可知，從O點起，P沿著中垂線逐漸遠離O點的過程中，P點處的合場強是先增大后減小，方向沿中垂線背離O點。所以，P點的合場強EP有最大值。下面我們給出兩種不同的數(shù)學解決方法。

4 結語

由上面解決問題的過程，我們發(fā)現(xiàn)，數(shù)學和物理是相互滲透的，物理問題里滲透著數(shù)學思想和數(shù)學方法，數(shù)學思想和方法在物理中有獨到的應用，這兩大學科之間的關系真的非常密切，在好多方面都是相輔相成的。我們在解決一些物理問題時，如果能做到抓住問題的本質(zhì)、處理得當，是可以把比較復雜甚至無法下手的物理問題輕松地轉(zhuǎn)化為比較熟悉的數(shù)學問題的，是可以降低解決問題的難度的。文中，筆者在探討等量的同種正電荷連線的垂直平分線上的點P處的電場強度的最大值問題時，就是運用物理概念和公式把問題的本質(zhì)剖析出來，建立電場強度這樣一個以距離為自變量的連續(xù)函數(shù)的數(shù)學模型，進而轉(zhuǎn)化為求電場強度連續(xù)函數(shù)在開區(qū)間內(nèi)的最值問題，然后分別借助于一元函數(shù)微積分學里的導數(shù)和不等式中的三元均值不等式巧妙地解決了文中提出的物理問題，所得結果也是一致的。

參考文獻：

[1]課程教材研究所物理課程教材研究開發(fā)中心.物理選修3-1[M].第三版.北京：人民教育出版社，2014：1-14.

[2]沈克琦.高中物理學（3）電磁學[M].合肥：中國科學技術大學出版社，2015：6-13.

[3]溫應春.高中物理一點一題型[M].合肥：中國科學技術大學出版社，2018：214-215.

[4]同濟大學應用數(shù)學系.高等數(shù)學（下）[M].第五版.北京：高等教育出版社，2002：152-160.

[5]李勝宏，邊紅平.平均值不等式與柯西不等式[M].第三版.上海：華東師范大學出版社，2020：1-3.

[6]單墫.代數(shù)不等式的證明[M].合肥：中國科學技術大學出版社，2017：12.