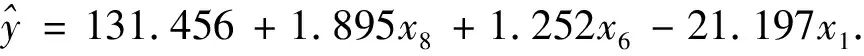基于逐步回歸方法下400米決賽成績的分析研究

潘 丹，熊江媛

(1.湖北師范大學 體育學院，湖北 黃石 435002；2.華南師范大學 體育科學學院，廣東 廣州 510631)

0 引言

2019年世界田徑錦標賽于2019年9月27日至10月26日在卡塔爾首都多哈舉行，世界田徑錦標賽每兩年舉辦一次，除了奧林匹克運動會以外，它是國際上最高級的田徑賽事，匯集了來自世界上能夠代表各個國家最高水平的田徑運動員，這些高水平運動員之間相互較量，能很大程度上反映出當今各個田徑項目的發展特點和趨勢。本文對男子400米決賽八名運動員的各段成績進行研究，試圖展示400米項目的發展趨向，從而精準地把握400米的訓練方向，在借鑒國外有效訓練方法的基礎上為提高我國男子400米跑的成績提供理論依據[1～3]。當今中國短跑項目已經發展到能與歐美各個國家相媲美，所以研究世界高水平短跑運動員的成績對我國有借鑒意義。

400米跑的各段成績也是研究400米跑能力的依據，大部分學者對400米分段成績的研究是從100米、200米角度研究的，近年來有不少文獻資料已經證明了我國短跑項目在起跑后的30～50米名列前茅，只有較少一部分學者提出研究50米分段成績對于提高運動員的400米成績具有重要作用，但并未結合我國短跑項目的優勢，研究出哪幾段50米與400米成績非常相關。因此，為了使我國400米運動員的比賽成績有所提高，本文在結合我國短跑優勢的基礎上以2019年世界田徑錦標賽男子400米決賽成績為研究對象，以50米為一段，整理相關數據，并對相關數據進行逐步回歸分析，剖析出哪幾段50米與400米成績呈顯著相關，建立回歸模型，為我國400米項目的訓練提供更加科學的指導。

1 研究對象及方法

1.1 研究對象

本文以2019年多哈田徑世界錦標賽男子400米決賽八名運動員在全程中各50米分段速度成績為對象建立模型組，包括第二道布魯姆費爾德(BLOOM FIELD)、第三道蓋伊(DEMISH GAYE)、第四道史蒂文加德納(STEVEN GARDINER)、第五道弗雷德克利(FRED KERLEY)、第六道馬謝爾塞多尼奧(MACHEL CEDENIO)、第七道基拉里詹姆斯(KIRANI JAMES)、第八道安東尼喬斯扎姆布拉默(ANTHONY JOSE ZAMBRANO)、第九道科里爾(KORIR)。

1.2 研究方法

1.2.1 文獻資料法 在中國知網上檢索了有關“短跑成績研究”“田徑400m”“田徑400米”“400m運動成績分段研究”為關鍵詞的相關期刊、碩博士論文以及與其相關的文章，根據在中國知網查閱關于400米分段研究的文獻資料，大多數學者選取影響400米成績的自變量為100米、200米、300米，較少學者選取50米為自變量進行分析，探討每段50米與400米成績的影響。因此本文將2019年世界田徑錦標賽男子400米決賽八名運動員的成績劃分為八個單獨的50米作為自變量，并運用一元線性回歸方程、二元線性回歸方程及逐步回歸方程對第八段50米和第六段50米進行比較與分析。

1.2.2 視頻解析法 在CCTV5體育賽事頻道官方網站上對2019年世界田徑錦標賽男子400m決賽視頻進行下載，視頻通過格式工廠轉換為AVIH格式后導入KINOVEA軟件，利用軟件對視頻進行剪輯與保存，將保存的視頻逐幀播放進行統計，利用DARTFISH軟件對視頻反復播放，將2019年世界田徑錦標賽男子400米決賽八名運動員的成績劃分為八個單獨的50米。通過視頻軟件中顯示的時間對各段50米的距離時間數據收集，同時結合國際田聯官網上關于2019年多哈世界田徑錦標賽男子400米決賽的其他相關統計數據，為本文提供數據支持。

1.2.3 數理統計法 借助Excel軟件，對搜集的各個數據進行分類處理，統計分析，為本文提供數理支持。對照組成績數據以均數±標準差表示，運用兩獨立樣本t檢驗分析，若P<0.05則表示顯著性差異，P<0.01則表示高度顯著性差異。

數據來源于國際田聯官網上關于2019年多哈世界田徑錦標賽男子400米決賽的相關統計數據。每一道次代表每名運動員，400米成績用y/s表示，第一段50米用x1/s表示、第二段50米成績用x2/s表示、第三段50米成績用x3/s表示、第四段50米成績用x4/s表示，第五段50米成績用x5/s表示，第六段50米成績用x6/s表示，第七段50米成績用x7/s表示，第八段50米成績用x8/s表示。如表 1所示。

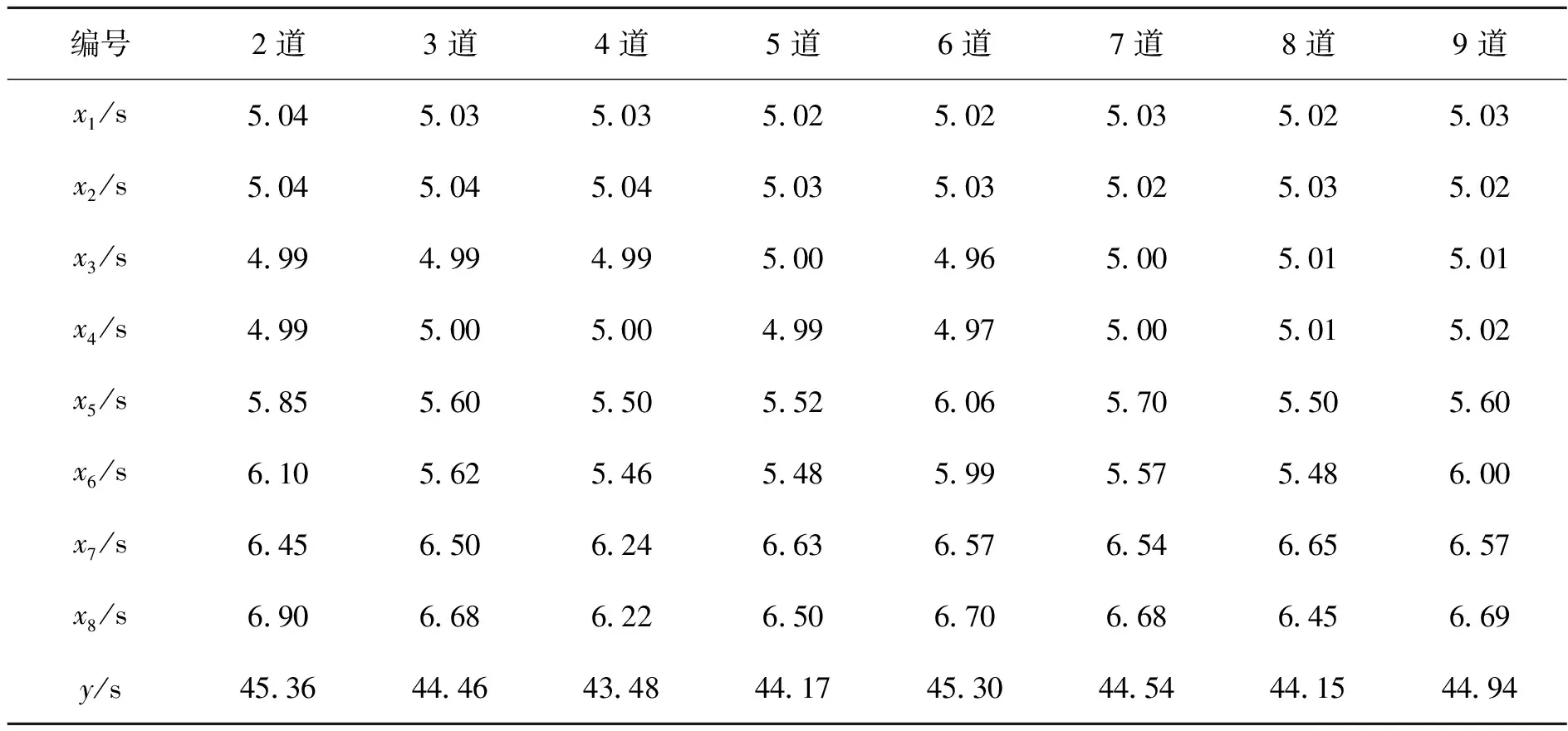
表1 400米成績回歸自變量

2 結果與分析

2.1 自變量“第八段50米”預測400米一元線性回歸方程

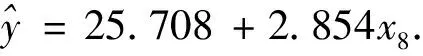
表2 第八段50米預測400米一元線性回歸方程方差分析表

經方差分析F=36.068，P<0.01，回歸方程非常顯著。第八段50米預測400米一元線性回歸方程的剩余標準差為0.259s.

2.2 自變量“第六段50米”預測400米一元線性回歸方程

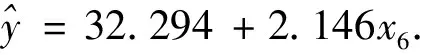
表3 第六段50米預測400米一元線性回歸方程方差分析表

經方差分析F=29.501，P<0.01，回歸方程非常顯著。第六段50米預測400米一元線性回歸方程的剩余標準差為0.282秒。

2.3 自變量“第八段50米”“第六段50米”預測400米二元線性回歸方程

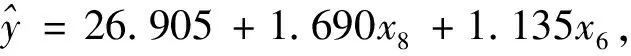
表4 二元線性回歸方程方差分析表

2.4 400米成績自變量逐步回歸分析

1)運用正交篩選法對Pearson相關又稱之為簡單相關系數R(0)選擇第一個自變量進入方程，計算其偏回歸平方和：

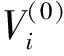
2)選擇第二個自變量進入回歸方程，計算偏回歸平方和:

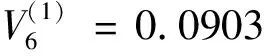
F=(8-3)×0.0903/(0.1425-0.0903)=8.6494>Fα=6.59,故自變量x6作用顯著，引入回歸方程中，對R(1)變換得R(2).

3)選擇第三個自變量進入回歸方程，計算偏回歸平方和：

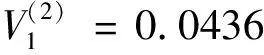
F=(8-4)×0.0436/(0.0522-0.0436)=20.2791>Fα=6.59，自變量x1作用顯著，引入回歸方程中，并對R(2)變換得R(3).

4)判斷是否應該從回歸方程中剔除變量，對已選入的自變量x8、x6、x1，計算他們的偏回歸平方和。

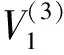
5)引入第四個自變量，對剩余的自變量x2、x3、x4、x5、x7，計算它們的偏回歸平方和。

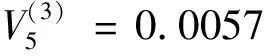
F=0.0057×(8-5)/0.0085-0.0057=6.1071

表5 逐步回歸方程方差分析表

2.5 一元線性回歸方程、二元線性回歸方程、逐步回歸方程模型預測400米成績比較結果

根據上述逐步回歸計算過程所得到的回歸方程，對2019年世界田徑錦標賽男子400米決賽實際成績數據(44.6686±0.4232)和回歸方程預測成績數據進行比較(44.6571±1.6998)。四個模型所預測的成績和實際比賽成績之間的相關系數P<0.01，表明模型預測成績和實際成績兩者之間有非常顯著的差異。

四個模型所預測的成績和實際比賽成績之間的配對t檢驗的結果是P>0.05，這說明模型預測成績和實際成績之間沒有明顯的顯著性差異，由此可見四個模型預測400米成績的實際效果較好。

逐步回歸方程預測成績與實際比賽成績之間的一致性相關系數0.9357最高，逐步回歸方程剩余標準差0.078s最小，這說明所建立的方程預測效果好、準確性高[4]。四種回歸方程模型預測400米能力的對比研究見表6.

表6 四種回歸方程模型預測400米能力的對比研究

2.6 逐步回歸分析結果的理論依據

400米第一個分段是起跑后的50米，這一階段和400米比賽中的最后沖刺階段同等關鍵。起跑所需要的成績對總成績的影響有著舉足輕重的作用，起跑時快速反應的能力可以使運動員在比賽中獲得有利速度的發揮身位[5]。因此，依據逐步回歸分析的結果，起跑這一階段在400米訓練中的重要作用也就顯而易見地表現出來。400米第六個分段是進入最后沖刺階段的關鍵所在。運動員跑完彎道所需時間要比跑完直道所用時間要多體力消耗更大，因此如果能有效地改善運動員的彎道跑技術，在訓練中加以強化，這樣運動員在彎道跑上所節省出來的部分時間，將會對短跑類項目的總成績有很大的幫助[6]。在400米彎道加速過程中,有效地運用彎道跑技術,是獲得優秀400米成績的重要因素之一[7]。因此，綜合前文逐步回歸分析結果的基礎上，第六段50米即最后彎道對400米成績的影響是至關重要的。400米第八個分段是沖刺跑最后50米，這一階段通常是影響400米成績的決定性因素。所以一直以來, 400米的運動員、教練員和體育科研人員都非常重視運動員最后沖刺能力的培養, 長期探索各種有效的訓練方法和手段，為提高運動員的速度耐力及骨骼肌的抗乳酸能力,通過不斷地訓練來提高400米運動員的比賽成績[8]。

3 結論