基于奔福德定律的航天物資采購價格風險分析

文/黃 娟 曹 建 顧笑一

隨著經營環境的不斷變化和國際化發展的不斷深入，航天企業的供應鏈和控制鏈大大延長，企業面臨的風險也日益增加。為進一步加強對國有資產的監督管理，國務院要求國有及國有控股企業應當加強內部監督和風險控制，國資委適時地頒布了《中央企業全面風險管理指引》。通過認真梳理與系統識別，航天企業構建了全面風險管理體系（宋欣等，2012），包括構建全面風險管理工作操作平臺和支撐保障體系，有效控制了戰略風險、市場風險、財務風險、型號風險、經營風險和法律風險等幾大類一級風險要素（唐煜，2020）。在二級風險目錄中，還著重提出了經費風險、價格風險、成本費用控制風險、物資采購控制風險等一百余項子風險。

航天企業作為典型的重工業、重資產類型企業，其產品及服務的實現過程中原材料及半成品的采購占有重要地位。有效合理的物資采購才能夠保證及時交貨，從而實現企業產品的物料流通，保證企業運轉和企業生產成本持續優化，實現企業存貨投資和損失的最小化，最終提高企業的盈利水平和市場競爭地位。航天企業的物資采購具有采購周期長、質量要求高、貨物種類多、成本占比大等特點（劉榮香，2019；王娜，2019），由此產生的價格風險不容忽視。針對上述特點，開展針對航天物資采購領域的價格風險研究，實現對價格風險的精細化管理十分重要。

一、奔福德定律簡介

1881年，美國學者Simon Newcomb發現，一本對數表手冊中前幾頁比后來的書頁更臟，人們使用的第一頁比最后一頁要多，人們似乎更頻繁地接觸以1開頭的數字。根據常識推斷，數字在整個數域中應該是均勻分布的，人們應該平均地查找它們。因此以1開頭的隨機數字和以2、3、……、9之間任何數開頭的隨機數字出現的概率應該是相同的。但這似乎并非事實，人們更頻繁地查找1，以1開頭的數字也更加常見。1938年，另一位美國學者Frank Benford偶然發現了相同的現象，Benford隨后搜集了大量來自不同來源的數值，包括世界上河流的流域面積、各個國家的人口密度、物理數學常數、不同年代的出生率和死亡率等，甚至搜集了出現在美國雜志文章中的數字，并進行了深入的研究，乃至發表了一系列的學術論文。經過大量的實證研究，最終形成了學界所公認的奔福德定律（Benford’s Law），即首位有效數字出現的概率，其數學表達式如式（1）所示：

式中，P(i)為首位有效數字為i的數出現的概率；i表示取值為1至9的自然數，即i＝1，…9。

目前，奔福德定律的應用相當廣泛。例如，通過W公司采購業務內部審計的真實案例，鄧佳軍（2018）介紹了奔福德定律(Benford’s law)的內涵及其在審計實務中的適用性。具體包括，應用奔福德定律時應注意，數據量必須足夠龐大，如10000條數據以上；另外訂單編號、發票編號等連續數據就不滿足奔福德定律。劉薇等人（2020）還結合H事務所的具體案例，通過應用奔福德定律幫助會計師事務所進行審計質量控制，尤其是優化業務承接決策，以此降低審計風險。吳國平（2019）總結指出，近二十年來國內外理論界將奔福德定律作為一種數值分析方法引入舞弊審計領域，產生了較多的相關研究文獻，但是基于傅利葉變換視角提出的一套理論解析框架，表明并非所有隨機過程產生的數據都符合奔福德定律，因此奔福德定律作為一種財務舞弊檢驗方法的理論依據還需進一步深入探討。

在醫學領域，有學者將奔福德定律應用于近期的新型冠狀病毒流行病學數據研究中，證明中國疾病預防控制中心的流行病學監測系統數據質量是可接受的（Idrovo等，2020）。Christoffer Koch等人（2020）進一步指出，部分媒體和外國政界人士對中國報道的有關COVID-19病例的數據表示懷疑，但是中國確診的感染病例數符合奔福德定律預期的分布，并且與美國和意大利的情況相似，因此沒有發現中國病例數被人為篡改的證據，對于決策者而言，信任中國實時報告的傳染性疾病數據非常重要。

在計算機信息領域，Fu等人（2007）討論了奔福德定律模型在圖像取證中的一些潛在應用，包括檢測位圖格式圖像的JPEG壓縮、估算JPEG壓縮位圖圖像的JPEG壓縮Q因子以及檢測雙壓縮JPEG圖像，還探討了參數對數定律，即廣義奔福德定律。廣泛的實驗結果證明了奔福德定律統計模型在圖像取證中的有效性。

二、工業品價格形成機制研究

為了驗證奔福德定律是否適用于大量的工業品價格數據，本文首先從機理上研究了工業品價格的形成規律。

工業品作為一種由市場分工的社會工業體系深加工產品，經歷了由原材料、半成品至成品的完整工序，還需要由上下游不同工廠之間分別辦理貨物進出口、倉儲、物流等多種流程，每一道工序或流程均提供了產品附加值，并形成了工業品的價格要素。工業品的價格組成要素示意圖如圖1所示，圖1中α1、α2、…、αn分別為不同工序或流程的成本定價系數，且αi均為大于或等于1的正實數。根據成本導向定價法，假設工業品以生產成本作為定價基礎。通常以單位產品的全部成本加上預計的利潤比率而計算出的；或者，只要工業品價格高于單位變動成本，產品的邊際收入就能大于零，銷量增加就能導致總收入的增加，從而獲利。例如，某種原材料采購成本為10元（α1=10），經過運輸后成本上升了10%（α2=1.1），成本價格變為11元，隨著深加工，成本再次上升100%（α3=2），成本價格變為22元，最終進入銷售環節，初步設定的銷售利潤為15%（α4=1.15），則產品價格最終為25.3元（即α1×α2×α3×α4=25.3）。

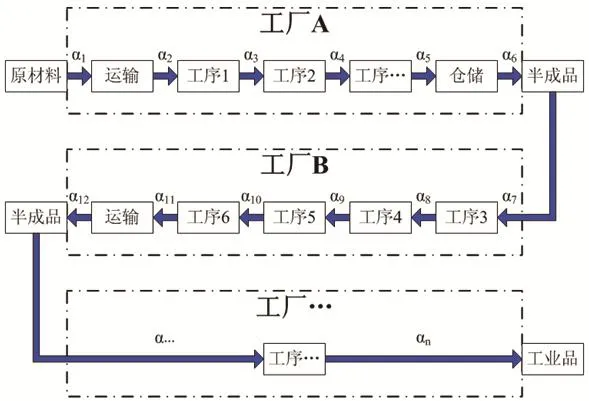
圖1 工業品價格組成要素示意圖

由于奔福德定律僅考慮有效數字的規律，因此不考慮數字的數量級情況。根據圖1中的模型，利用EXCEL軟件模擬生成了n組大于或等于1的隨機數，每組的數據量為10000個，如表1所示。假定上述隨機數即為不同工序或流程的成本定價系數，n為工序或流程的種類數目，由人工設定為遞增函數，分別取值為1、2、4、8、16和32。工業品價格的數學定量表達式如式（2）所示：

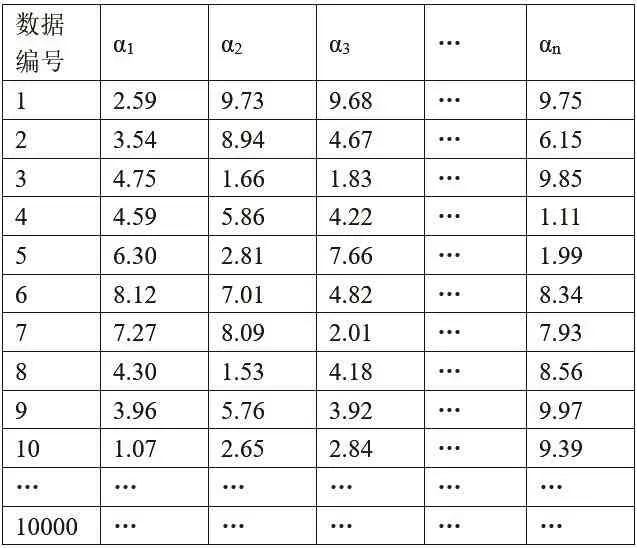
表1 隨機生成的成本定價系數

式中，C為成本定價法的工業品價格；αk為工序或流程的成本定價系數，且αk≥1；k為序號，代表不同工序，k＝1，2，…，n；n為工序總數，在本文中的最大取值為32。計算中，n的數值從小到大逐漸變化，利用奔福德定律對隨機數模擬生成的工業品價格首位數分布規律進行檢驗，結果如圖2所示。

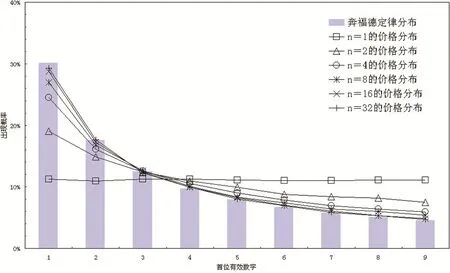
圖2 n個成本定價系數形成的工業品價格分布

由圖2可知，如果n為1時，工業品價格的首位數字分布近似為1至9的均勻分布，和一般隨機數生成的規律一致。隨著n的不斷增加，工業品價格的首位數分布規律越來越趨近奔福德定律。即在社會化大生產的條件下，如果工序流程較復雜，經歷了多次成本附加過程，那么，該類工業品價格首位有效數字的分布規律是符合奔福德定律的。

三、航天物資采購價格校驗

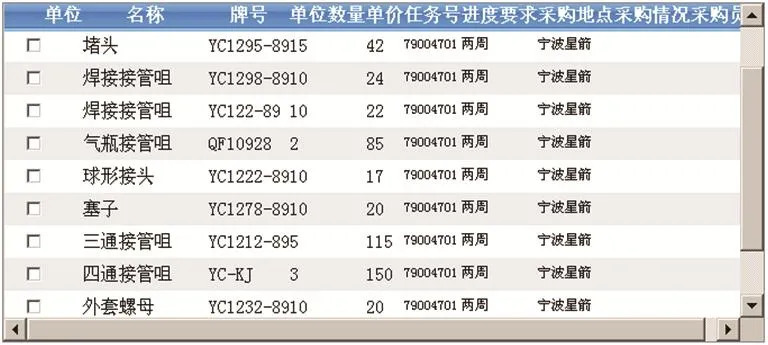
在此基礎上，利于EXCEL軟件統計了航天某研究所近3年實際發生的一萬余條物資采購數據，采購數據模板如圖3所示，分別提取了其中的單價數值形成一個單價數據集，并對該數據集中各有效數字的首位數進行了統計計算，結果如表2所示。得到航天物資采購價格的首位數出現概率后，根據式（3）計算出該概率分布與奔福德定律的偏差情況：

式中，F為對比可信度，F≤100%；j表示取值分別為1至9，即j＝1，2，…，9；Rj為航天物資采購價格中首位數為j的個數比例；Bj為奔福德定律中首位數為j的分布概率；m代表1至9的自然數總個數，即m=9。

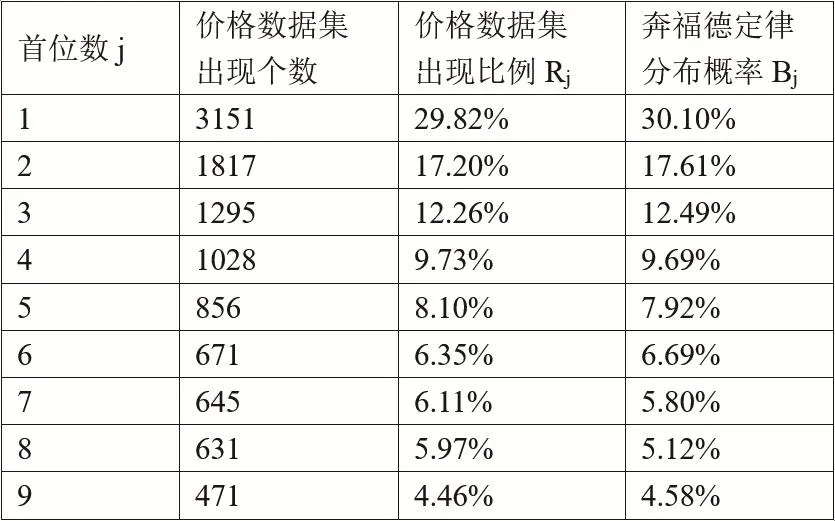
表2 航天物資采購價格的首位數分布

根據式（3）計算得出，航天物資采購價格的首位數出現概率分布對比可信度約為95.6%，可信度越大，說明數據信息體現的價格風險越小，可信度的置信區間一般定義為大于或等于95%，此時該價格數據基本不存在人為造假。

四、結語

本文首先假設了一種社會化生產的工業品價格形成機理，即成本導向定價法，假設工業品以生產成本作為定價基礎，以單位產品所經歷的各個工序的全部成本（含預計的利潤比率）依次加權而計算得出。通過數值模擬，發現按照加權模型計算得出的10000件工業品價格首位有效數字分布符合奔福德定律。據此，繼續利用奔福德定律，探索了一種研究航天物資采購價格風險的新方法。奔福德定律的應用，可以使內部審計及風險控制人員從整體上把握被審計數據的具體情況，快速發現可疑數據，提高工作效率。利用該方法對航天某單位近3年的物資采購數據進行統計分析，結果顯示航天物資采購價格的首位數出現概率分布與奔福德定律的理論分布概率相比，可信度約為95.6%，即采購價格數據基本不存在人為造假。該實例證明了應用奔福德定律在航天物資采購價格審計和內部控制中具有較好的便捷性和實用性。