驅(qū)動(dòng)控制對(duì)太陽(yáng)帆板驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性的影響*
朱仕堯,郭 欣,雷勇軍
(國(guó)防科技大學(xué) 空天科學(xué)學(xué)院, 湖南 長(zhǎng)沙 410073)
太陽(yáng)帆板驅(qū)動(dòng)系統(tǒng)(Solar Array Drive System,SADS)一般由太陽(yáng)帆板及其驅(qū)動(dòng)裝置(Solar Array Drive Assembly,SADA)組成。SADA內(nèi)部激擾因素會(huì)產(chǎn)生附加的擾動(dòng)力矩,造成太陽(yáng)帆板運(yùn)動(dòng)不平穩(wěn),引起結(jié)構(gòu)振動(dòng)擾動(dòng);而太陽(yáng)帆板結(jié)構(gòu)振動(dòng)又會(huì)反過來影響太陽(yáng)帆板運(yùn)行平穩(wěn)性和擾動(dòng)力矩幅值,降低高精度航天器指向精度、成像質(zhì)量或通信頻率等性能指標(biāo)[1]。開展驅(qū)動(dòng)系統(tǒng)擾振特性分析和有效抑制擾動(dòng)力矩都需要首先準(zhǔn)確分析驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性。
太陽(yáng)帆板驅(qū)動(dòng)系統(tǒng)包括太陽(yáng)帆板轉(zhuǎn)動(dòng)引入的剛?cè)狁詈闲?yīng)、SADA閉環(huán)伺服驅(qū)動(dòng)控制以及SADA和太陽(yáng)帆板之間的動(dòng)力耦合等多種耦合因素[2],這些因素會(huì)對(duì)其系統(tǒng)動(dòng)力學(xué)特性產(chǎn)生影響,增加系統(tǒng)動(dòng)力學(xué)特性的分析難度。在早期研究中,SADA往往被考慮為剛性體,不考慮SADA與太陽(yáng)帆板的動(dòng)力耦合,驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性僅表現(xiàn)為太陽(yáng)帆板結(jié)構(gòu)模態(tài)特征,可以采用集中參數(shù)模型[3]、模態(tài)坐標(biāo)模型[4]、懸臂歐拉梁模型[5]、固支-自由-自由-自由邊界的基爾霍夫板模型[6]以及有限元模型[7-8]等表征。隨著SADA研究不斷深入,研究人員開始關(guān)注SADA自身的剛度和阻尼特征。這些研究往往采用剛性附件代替柔性太陽(yáng)帆板。Low[9]、Yang[10]和Middleton[11]等主要研究了由步進(jìn)電機(jī)內(nèi)部機(jī)電耦合引起的電磁剛度和阻尼特性。Cabilic[12]和Wood[13]等證明了SADA內(nèi)部滑環(huán)結(jié)構(gòu)的摩擦?xí)腩~外的阻尼。Lu等[14]研究了驅(qū)動(dòng)系統(tǒng)減速裝置齒輪咬合間隙對(duì)擾動(dòng)特性的影響。近些年,研究人員開始探索在系統(tǒng)動(dòng)力學(xué)分析中綜合考慮SADA和太陽(yáng)帆板的結(jié)構(gòu)特性。Sattar[15]、Chen[16]和Li[17]等研究了帶有柔性負(fù)載的驅(qū)動(dòng)系統(tǒng)擾動(dòng)特性問題,其中采用集中參數(shù)模型模擬柔性負(fù)載,對(duì)步進(jìn)電機(jī)進(jìn)行線性化處理,獲得其等效電磁剛度。Zhu等[2, 18]在理想控制假設(shè)和穩(wěn)態(tài)運(yùn)動(dòng)假設(shè)下,推導(dǎo)了SADA的等效剛度和等效阻尼,并提出了一種驅(qū)動(dòng)系統(tǒng)動(dòng)特性分析方法。以上研究往往將驅(qū)動(dòng)系統(tǒng)限定在低轉(zhuǎn)速模式,對(duì)驅(qū)動(dòng)控制進(jìn)行理想化假設(shè),以簡(jiǎn)化問題難度。Zhou等[19]利用輸入成形器對(duì)驅(qū)動(dòng)控制指令進(jìn)行預(yù)處理,以減少快速驅(qū)動(dòng)后的殘余振動(dòng)擾動(dòng),但未對(duì)快速捕獲或轉(zhuǎn)角歸零等高轉(zhuǎn)速模式下的驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性進(jìn)行討論。
針對(duì)上述問題,本文摒棄驅(qū)動(dòng)控制理想化假設(shè),重點(diǎn)推導(dǎo)考慮驅(qū)動(dòng)控制因素的SADA等效力學(xué)特性參數(shù),構(gòu)建SADS動(dòng)力學(xué)特性等效分析模型,通過仿真和試驗(yàn)驗(yàn)證模型正確性,并研究不同轉(zhuǎn)速條件下驅(qū)動(dòng)控制增益對(duì)SADS動(dòng)力學(xué)特性的影響規(guī)律,對(duì)工程型號(hào)改進(jìn)設(shè)計(jì)、擾振特性分析以及振動(dòng)控制研究具有重要參考價(jià)值。
1 驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性等效分析模型
1.1 驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)模型
SADS坐標(biāo)系定義如圖1所示,其中OXYZ為慣性坐標(biāo)系,oxyz為太陽(yáng)帆板隨體坐標(biāo)系。航天器本體的質(zhì)量和頻率特性均明顯大于SADS,可將其簡(jiǎn)化為固定約束的剛性體。根據(jù)SADS工作流程(如圖2所示)可知,系統(tǒng)動(dòng)力學(xué)模型可由驅(qū)動(dòng)控制、驅(qū)動(dòng)裝置和太陽(yáng)帆板等子模型組成。

圖1 太陽(yáng)帆板驅(qū)動(dòng)系統(tǒng)組成Fig.1 System composition of SADS

圖2 驅(qū)動(dòng)系統(tǒng)工作流程Fig.2 Typical workflow of SADS
1.1.1 驅(qū)動(dòng)控制
SADA一般采用步進(jìn)電機(jī)作為驅(qū)動(dòng)執(zhí)行部件。由于其每個(gè)輸入脈沖所對(duì)應(yīng)的轉(zhuǎn)角是定值,因此脈沖信號(hào)的頻率與驅(qū)動(dòng)速度成正比,可以通過開環(huán)控制實(shí)現(xiàn)驅(qū)動(dòng)速度控制。為避免步進(jìn)驅(qū)動(dòng)引起較大幅度的力矩波動(dòng),電流細(xì)分器對(duì)步進(jìn)電機(jī)參考電流進(jìn)行微步階躍形式的三角函數(shù)細(xì)分。如圖3所示,隨著電流細(xì)分?jǐn)?shù)的增加,參考電流細(xì)分階躍幅度逐漸減小。

圖3 電流細(xì)分?jǐn)?shù)對(duì)參考電流的影響Fig.3 Relationship between current fraction and reference current

(1)
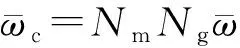
在參考電流細(xì)分基礎(chǔ)上,電流控制器通過步進(jìn)電機(jī)繞組電流與參考電流之間的偏差反饋調(diào)整驅(qū)動(dòng)電壓(以下簡(jiǎn)稱為電流環(huán)),使繞組電流跟隨參考電流變化,從而保證驅(qū)動(dòng)速度與實(shí)際轉(zhuǎn)速趨于一致。根據(jù)電機(jī)的電壓平衡方程可以得到實(shí)際電流ij的表達(dá)式:

(2)
式中:R和L分別為繞組阻抗和電感系數(shù);Km為電磁力矩系數(shù);ωm和θm分別為電機(jī)轉(zhuǎn)子轉(zhuǎn)速和轉(zhuǎn)角。設(shè)定電流控制器采用PI控制律調(diào)整驅(qū)動(dòng)電壓uj:
(3)
式中:KP和KI分別為比例和積分控制增益。
1.1.2 驅(qū)動(dòng)裝置
含有減速裝置的SADA力矩平衡方程[20]為:
(4)
式中:Tl為驅(qū)動(dòng)力矩;Jm為轉(zhuǎn)子轉(zhuǎn)動(dòng)慣量;ρg為減速裝置傳遞效率;電磁力矩Te和摩擦力矩Tf分別表示為
(5)
Tf=σ0ωl-[Tc+(Ts-Tc)e-(ωl/ωs)]sgn(ωl)
(6)
其中:σ0為黏性摩擦系數(shù);Tc和Ts分別為庫(kù)倫摩擦力矩和最大靜摩擦力矩;ωs為臨界Strebeck轉(zhuǎn)速。
含有減速裝置的SADA運(yùn)動(dòng)方程為:
(7)
其中:ωl和θl分別為太陽(yáng)帆板轉(zhuǎn)速和轉(zhuǎn)角。
1.1.3 太陽(yáng)帆板
根據(jù)虛功原理,當(dāng)不考慮高階小量時(shí),可以建立考慮太陽(yáng)帆板剛體轉(zhuǎn)動(dòng)、柔性振動(dòng)以及兩者耦合的柔性太陽(yáng)帆板結(jié)構(gòu)動(dòng)力學(xué)模型[2]:
(8)
式中:Hl為模態(tài)角動(dòng)量矩陣H第一行向量;Jl為轉(zhuǎn)動(dòng)慣性矩陣J第一個(gè)對(duì)角元;η為太陽(yáng)帆板模態(tài)坐標(biāo);D和Λ分別為模態(tài)阻尼矩陣和特征值矩陣。 將式(4)代入式(8),并結(jié)合式(1)~(3)得SADS動(dòng)力學(xué)模型。
1.2 步進(jìn)電機(jī)繞組電流表達(dá)式
穩(wěn)態(tài)太陽(yáng)帆板驅(qū)動(dòng)系統(tǒng)運(yùn)動(dòng)具有如下特點(diǎn):
(9)
此時(shí)電機(jī)實(shí)際轉(zhuǎn)速和平均驅(qū)動(dòng)速度之間的誤差很小,即電機(jī)轉(zhuǎn)動(dòng)的運(yùn)動(dòng)規(guī)律滿足如下關(guān)系:
(10)
將式(10)代入式(2),可近似得到:
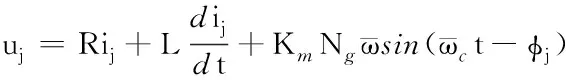
(11)
再將式(11)代入式(3),可整理得到:
(12)
如圖4所示,充分細(xì)分后的穩(wěn)態(tài)繞組電流可以近似為與參考電流同頻振蕩、但幅值和相位不同的三角函數(shù),因此第j相繞組電流為:
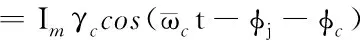
(13)
式中,γc和φc分別為繞組電流相對(duì)參考電流的幅值比和延遲相位,其與參數(shù)P和Q的關(guān)系式為:
(14)

圖4 繞組電流和參考電流時(shí)間歷程曲線Fig.4 Time history curves of winding and reference current
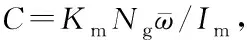
(15)
式(15)只有在正弦項(xiàng)和余弦項(xiàng)系數(shù)同時(shí)為0的情況下才能成立,可以列寫代數(shù)方程組并求解得到:
(16)
進(jìn)一步將式(16)代入式(14),可以得到驅(qū)動(dòng)控制增益、繞組特性以及轉(zhuǎn)速等參數(shù)與繞組電流幅值和相位的關(guān)系。
1.3 驅(qū)動(dòng)裝置等效力學(xué)特性
以兩相混合式步進(jìn)電機(jī)為例,將式(13)代入式(5)可得電磁力矩為:
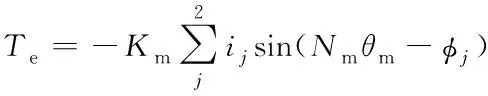
(17)
因此式(4)中的驅(qū)動(dòng)力矩可整理為:
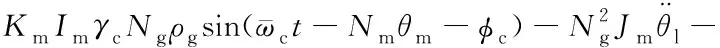
σ0ωl-[Tc+(Ts-Tc)e-(ωl/ωs)]sgn(ωl)
(18)

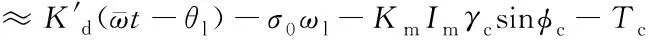
(19)
式中:轉(zhuǎn)速ωl系數(shù)的絕對(duì)值σ0為考慮驅(qū)動(dòng)控制后的SADA等效阻尼;轉(zhuǎn)角θl系數(shù)的絕對(duì)值K′d為SADA等效剛度,具體表達(dá)式為
(20)

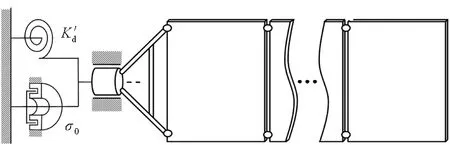
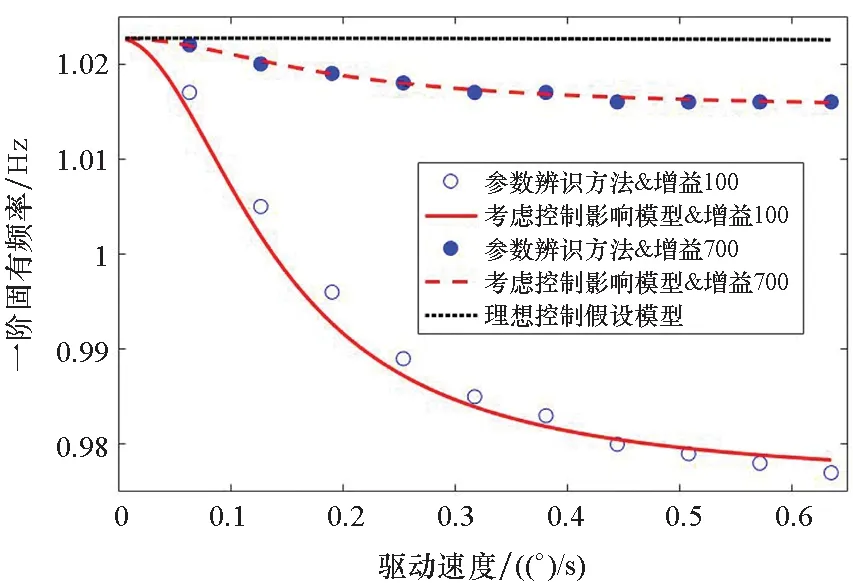
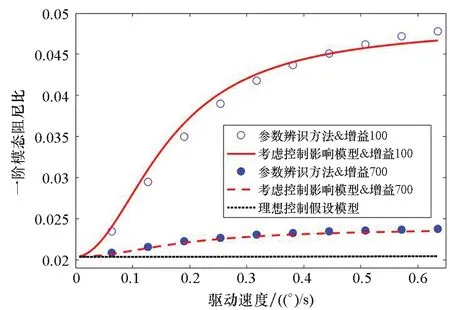
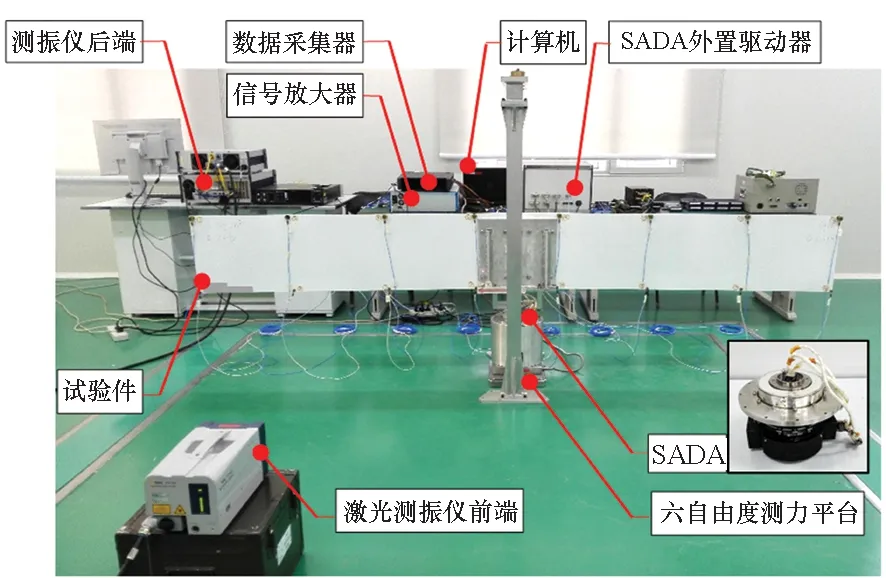
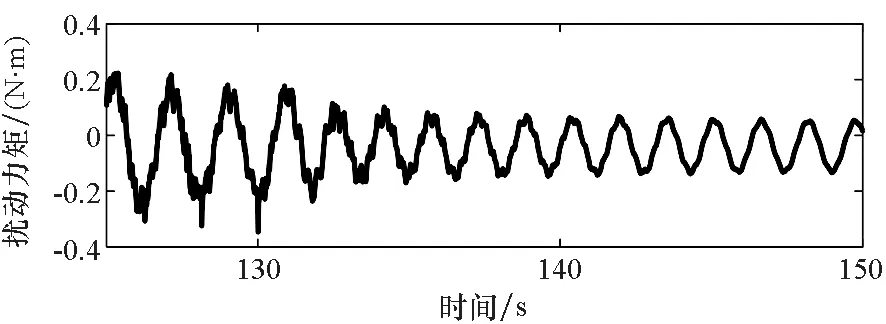
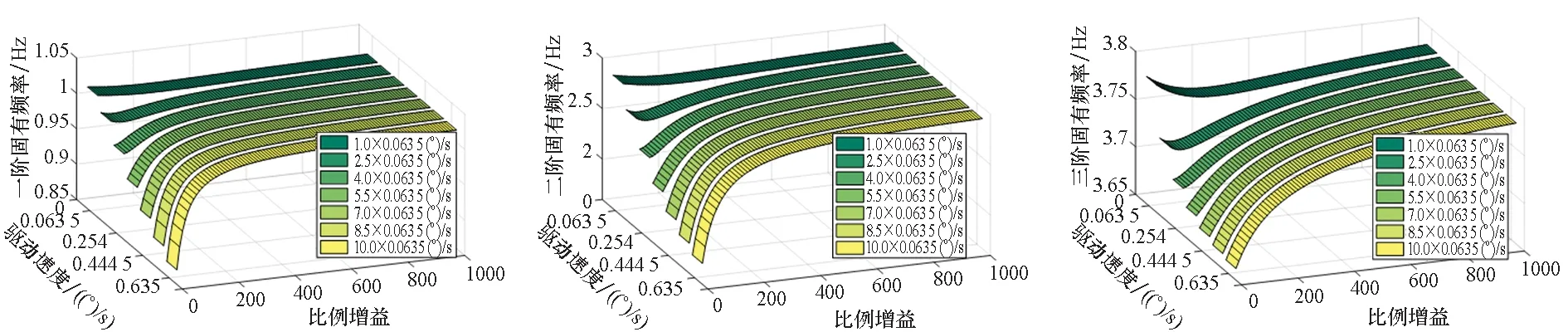
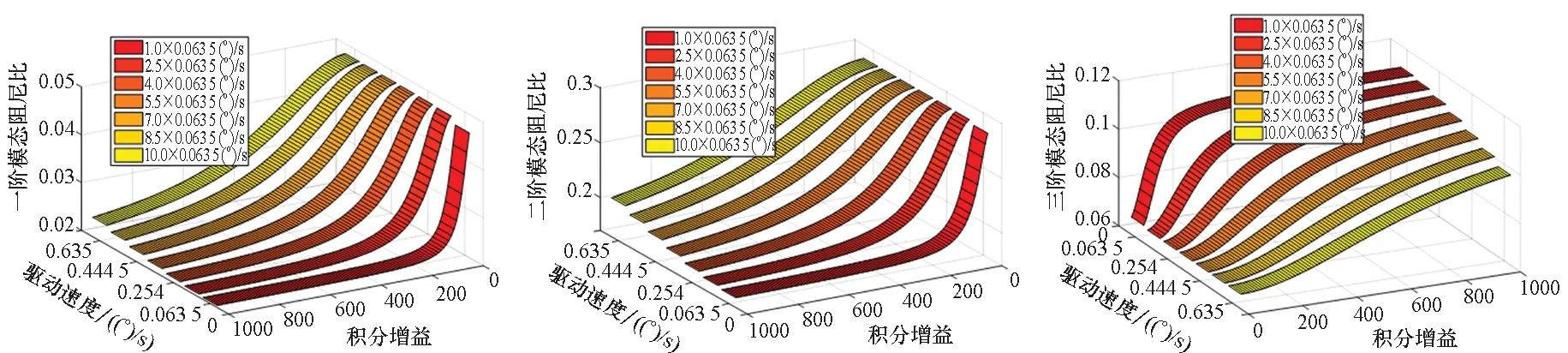
由于0 將式(19)代入式(8),可得SADS動(dòng)力學(xué)特性等效分析模型: (21) 圖5 驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性等效模型Fig.5 Dynamic-characteristics equivalent model of SADS 圖6給出了分別采用參數(shù)辨識(shí)方法、考慮驅(qū)動(dòng)控制的等效模型和基于理想驅(qū)動(dòng)控制假設(shè)的等效模型得到的驅(qū)動(dòng)系統(tǒng)一階扭轉(zhuǎn)模態(tài)固有頻率和模態(tài)阻尼比隨驅(qū)動(dòng)速度的變化曲線。由圖可知:①在驅(qū)動(dòng)速度趨近0.063 5 (°)/s且控制增益為700時(shí),三者計(jì)算得到的驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性參數(shù)吻合較好。②隨著驅(qū)動(dòng)速度逐漸增大,參數(shù)辨識(shí)結(jié)果與考慮驅(qū)動(dòng)控制的等效模型所得動(dòng)特性變化規(guī)律一致,固有頻率均隨驅(qū)動(dòng)速度增大而逐漸減小,模態(tài)阻尼比隨驅(qū)動(dòng)速度增大而逐漸增大;且控制增益越小,模態(tài)參數(shù)變化幅度越大。然而,基于理想驅(qū)動(dòng)控制假設(shè)的等效模型所得系統(tǒng)模態(tài)參數(shù)均不隨轉(zhuǎn)速和控制增益變化,其與參數(shù)辨識(shí)的相對(duì)誤差隨驅(qū)動(dòng)速度增大和控制增益減小而增大。③在驅(qū)動(dòng)速度趨近0.635 (°)/s時(shí),參數(shù)辨識(shí)和考慮驅(qū)動(dòng)控制的等效模型所得固有頻率的相對(duì)誤差為-2.32%,阻尼比相對(duì)誤差為-1.88%;而基于理想驅(qū)動(dòng)控制假設(shè)的等效模型所得固有頻率和阻尼比與參數(shù)辨識(shí)方法的相對(duì)誤差分別可達(dá)4.71%和-57.11%。以上分析說明:基于理想驅(qū)動(dòng)控制假設(shè)的等效模型在驅(qū)動(dòng)速度增大后出現(xiàn)應(yīng)用局限性,而考慮驅(qū)動(dòng)控制的等效模型可以適應(yīng)驅(qū)動(dòng)速度和控制增益的變化。 (a) 一階固有頻率(a) 1st natural frequency (b) 一階模態(tài)阻尼比(b) 1st model damping ratio圖6 系統(tǒng)動(dòng)力學(xué)特性參數(shù)與轉(zhuǎn)速關(guān)系曲線Fig.6 Relationship curve between dynamic characteristic of SADS and rotational speed 試驗(yàn)件為驅(qū)動(dòng)裝置和太陽(yáng)帆板模擬件構(gòu)成的驅(qū)動(dòng)系統(tǒng)(如圖7所示)。驅(qū)動(dòng)裝置為低軌直接型SADA;太陽(yáng)帆板由兩塊鋁合金薄板組成,用于模擬太陽(yáng)帆板在驅(qū)動(dòng)方向的質(zhì)量和剛度特征,滿足轉(zhuǎn)動(dòng)慣量等效和結(jié)構(gòu)基頻等效原則。為抵消模擬件對(duì)驅(qū)動(dòng)裝置軸承的壓力,在驅(qū)動(dòng)系統(tǒng)的轉(zhuǎn)動(dòng)軸線方向配備龍門吊和吊裝組件以卸載重力。 測(cè)試系統(tǒng)由Kistler六自由度測(cè)力平臺(tái)、Polytec激光測(cè)振儀、信號(hào)放大器、數(shù)據(jù)采集器、計(jì)算機(jī)和SADA外置驅(qū)動(dòng)器以及動(dòng)力學(xué)試驗(yàn)分析軟件等組成,如圖7所示。測(cè)力平臺(tái)通過螺栓與SADA轉(zhuǎn)接工裝固定連接,用于測(cè)量驅(qū)動(dòng)系統(tǒng)的擾動(dòng)力矩分量。激光測(cè)振儀測(cè)量驅(qū)動(dòng)裝置轉(zhuǎn)速,激光測(cè)點(diǎn)布置在太陽(yáng)帆板剛性轉(zhuǎn)接工裝上。測(cè)量結(jié)果分別經(jīng)過信號(hào)放大器和測(cè)振儀后置端進(jìn)行處理,并通過數(shù)據(jù)采集器傳遞給計(jì)算機(jī)。SADA外置驅(qū)動(dòng)器用于產(chǎn)生脈沖信號(hào)控制太陽(yáng)帆板轉(zhuǎn)動(dòng)。 圖7 驅(qū)動(dòng)系統(tǒng)擾動(dòng)特性測(cè)試系統(tǒng)Fig.7 Disturbance-characteristics test system of SADS 在驅(qū)動(dòng)系統(tǒng)勻速驅(qū)動(dòng)后增加停止指令,記錄驅(qū)動(dòng)系統(tǒng)在停止段的殘余振動(dòng)響應(yīng),并對(duì)該段自由振動(dòng)數(shù)據(jù)(如圖8所示)進(jìn)行傅里葉變換得到頻譜分布特征。擾動(dòng)力矩衰減曲線表現(xiàn)為單頻震蕩特點(diǎn),幅度隨時(shí)間增加而逐漸減小;在頻譜曲線低頻段存在明顯峰值,所對(duì)應(yīng)頻率0.656 Hz即為驅(qū)動(dòng)系統(tǒng)基頻。參考試驗(yàn)狀態(tài)建立太陽(yáng)帆板模擬件與驅(qū)動(dòng)裝置等效剛度和阻尼模型。根據(jù)文獻(xiàn)[2]參數(shù)確定驅(qū)動(dòng)裝置等效剛度為680 N·m/rad,等效阻尼為60 N·m·s/rad。通過模態(tài)分析得到其在固定支撐邊界條件下的動(dòng)力學(xué)特性,其中一階模態(tài)振型同為圍繞驅(qū)動(dòng)方向的一階扭轉(zhuǎn)振動(dòng),對(duì)應(yīng)基頻為0.610 Hz,與試驗(yàn)結(jié)果相對(duì)誤差為-7.01%。 (a) 時(shí)間歷程(a) Time history (b) 頻譜分布(b) Frequency spectrum圖8 驅(qū)動(dòng)系統(tǒng)停止段擾動(dòng)力矩Fig.8 Disturbance torque in the stop phase of SADS 圖9給出了不同驅(qū)動(dòng)速度下SADS各階扭轉(zhuǎn)模態(tài)固有頻率隨比例增益的變化曲線。由圖可知:①驅(qū)動(dòng)速度大于4倍0.063 5 (°)/s時(shí),前兩階固有頻率先隨比例增益顯著增大而后逐漸趨于穩(wěn)定,最小的固有頻率取值位于最小的比例增益位置并隨驅(qū)動(dòng)速度減小而增大,且固有頻率趨于平穩(wěn)時(shí)的臨界比例增益取值隨模態(tài)階數(shù)增大而增大;第三階固有頻率在所見區(qū)域內(nèi)始終與比例增益成正相關(guān)關(guān)系,未出現(xiàn)穩(wěn)定階段。②驅(qū)動(dòng)速度小于4倍0.063 5 (°)/s時(shí),固有頻率均隨比例增益先微幅減小而后趨于穩(wěn)定。以上分析說明:驅(qū)動(dòng)系統(tǒng)固有頻率僅在驅(qū)動(dòng)速度較大且比例增益較小時(shí)才會(huì)變化;當(dāng)比例增益增大后,固有頻率不隨驅(qū)動(dòng)速度和比例增益而改變。 圖10給出了不同驅(qū)動(dòng)速度下SADS各階扭轉(zhuǎn)模態(tài)阻尼比隨比例增益的變化曲線。由圖可知:①驅(qū)動(dòng)速度大于4倍0.063 5 (°)/s時(shí),前兩階模態(tài)阻尼比隨比例增益增大而顯著減小,隨后保持穩(wěn)定;在驅(qū)動(dòng)速度小于4倍0.063 5 (°)/s時(shí),模態(tài)阻尼比先小幅增大而后趨于平穩(wěn),且穩(wěn)定值按模態(tài)階次順序逐漸增大。②第三階模態(tài)阻尼比的變化趨勢(shì)與前兩階相反,其在驅(qū)動(dòng)速度大于4倍0.063 5 (°)/s時(shí),隨比例增益增大而增大;在驅(qū)動(dòng)速度小于4倍0.063 5 (°)/s時(shí),第三階模態(tài)阻尼比先小幅減小然后趨于穩(wěn)定;模態(tài)阻尼比最小值對(duì)應(yīng)比例增益的最小值,并隨驅(qū)動(dòng)速度增大而減小。以上分析說明:各階模態(tài)阻尼比的變化趨勢(shì)并不相同,但是都會(huì)在比例增益較小且驅(qū)動(dòng)速度較大時(shí)發(fā)生變化,在比例增益大于特定值后趨于穩(wěn)定。 圖11為不同驅(qū)動(dòng)速度下SADS各階扭轉(zhuǎn)模態(tài)固有頻率隨積分增益的變化曲線。由圖可知:①當(dāng)驅(qū)動(dòng)速度較小時(shí),固有頻率逐漸增大并最終達(dá)到穩(wěn)定取值;②隨著驅(qū)動(dòng)速度的增大,固有頻率增大速度在逐漸減小,特別是當(dāng)驅(qū)動(dòng)速度大于5.5倍0.063 5 (°)/s后,固有頻率在所研究范圍內(nèi)始終隨積分增益增大,而未趨于穩(wěn)定。 圖12為不同驅(qū)動(dòng)速度下SADS各階扭轉(zhuǎn)模態(tài)阻尼比隨積分增益的變化曲線。由圖可知:①前兩階模態(tài)阻尼比均隨積分增益增大而減小,且減小速率隨驅(qū)動(dòng)速度增大而逐漸減小;同階模態(tài)阻尼比最大值均對(duì)應(yīng)積分增益最小值;驅(qū)動(dòng)速度增大會(huì)使模態(tài)阻尼比最小值不斷增大。②第三階模態(tài)阻尼比隨著積分增益的增大而增大;在最小驅(qū)動(dòng)速度工況下,其首先隨積分增益顯著增大,然后趨于穩(wěn)定;隨驅(qū)動(dòng)速度增大,模態(tài)阻尼比增大速率不斷減小;在最大驅(qū)動(dòng)速度工況下,模態(tài)阻尼比隨積分增益增大而平穩(wěn)增加。 (a) 第一階固有頻率(a) 1st natural frequency (b) 第二階固有頻率(b) 2nd natural frequency (c) 第三階固有頻率(c) 3rd natural frequency圖9 比例控制增益對(duì)系統(tǒng)固有頻率的影響Fig.9 Relationship between the proportional gain and the natural frequency of SADS (a) 第一階模態(tài)阻尼比(a) 1st model damping ratio (b) 第二階模態(tài)阻尼比(b) 2nd model damping ratio (c) 第三階模態(tài)阻尼比(c) 3rd model damping ratio圖10 比例控制增益對(duì)系統(tǒng)模態(tài)阻尼的影響Fig.10 Relationship between the proportional gain and the model damping ratio of SADS (a) 第一階模態(tài)阻尼比(a) 1st model damping ratio (b) 第二階模態(tài)阻尼比(b) 2nd model damping ratio (c) 第三階模態(tài)阻尼比(c) 3rd model damping ratio圖12 積分控制增益對(duì)系統(tǒng)模態(tài)阻尼的影響Fig.12 Relationship between the integral gain and the model damping ratio of SADS 針對(duì)驅(qū)動(dòng)控制對(duì)太陽(yáng)帆板驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性影響問題,構(gòu)建了動(dòng)力學(xué)特性等效分析模型,開展了模型正確性驗(yàn)證,分析了控制增益和驅(qū)動(dòng)速度對(duì)驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性的影響規(guī)律。主要結(jié)論如下: 1)驅(qū)動(dòng)控制不會(huì)改變驅(qū)動(dòng)裝置的等效阻尼,但會(huì)使驅(qū)動(dòng)裝置等效剛度減弱,且減弱程度與驅(qū)動(dòng)速度成正比,與控制增益成反比。 2)所構(gòu)建的等效分析模型能夠在不同驅(qū)動(dòng)速度和控制增益情況下準(zhǔn)確預(yù)示驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性,分析結(jié)果與試驗(yàn)數(shù)據(jù)誤差小于10%。 3)驅(qū)動(dòng)系統(tǒng)固有頻率與控制增益成正相關(guān)關(guān)系,與驅(qū)動(dòng)速度成負(fù)相關(guān)關(guān)系。 本研究擴(kuò)展了驅(qū)動(dòng)系統(tǒng)動(dòng)力學(xué)特性分析理論的工程適用范圍,可以為具體工程型號(hào)的擾振特性分析以及振動(dòng)控制方案設(shè)計(jì)提供理論支撐和技術(shù)參考。1.4 動(dòng)力學(xué)特性等效分析模型
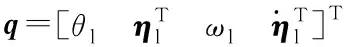
2 動(dòng)力學(xué)特性分析模型正確性驗(yàn)證
2.1 仿真驗(yàn)證
2.2 試驗(yàn)驗(yàn)證

3 驅(qū)動(dòng)控制對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響分析
3.1 驅(qū)動(dòng)速度和比例增益對(duì)系統(tǒng)動(dòng)力學(xué)特性影響
3.2 驅(qū)動(dòng)速度和積分增益對(duì)系統(tǒng)動(dòng)力學(xué)特性影響

4 結(jié)論

