BDS/INS緊組合三頻動對動模糊度解算方法*

趙修斌,朱楚江,龐春雷,張 良,高玉潔

(1. 空軍工程大學 信息與導航學院， 陜西 西安 710077； 2. 中國人民解放軍95140部隊， 廣東 惠州 516211)

基于載波相位差分的動對動相對定位技術(shù)在飛機精密編隊飛行、空中加油、空間飛行器交會對接和艦載機著艦等領(lǐng)域具有重要應用，其關(guān)鍵在于動對動條件下整周模糊度的快速解算[1-3]。目前，我國北斗衛(wèi)星導航系統(tǒng)正在迅猛發(fā)展，已經(jīng)可以在B1、B2、B3三個頻點上播發(fā)衛(wèi)星導航信號，以提供更精確的導航定位服務。三頻信號能夠提供額外頻點的載波相位觀測值，從而為整周模糊度的解算提供了極大便利[4-5]。針對三頻整周模糊度解法，國內(nèi)外學者已經(jīng)進行了大量研究，其中最具代表性的是三頻整周模糊度解法(Three Carrier Ambiguity Resolution， TCAR)和級聯(lián)模糊度算法(Cascading Integer Resolution, CIR)[6-7]。在此基礎(chǔ)上，姚一飛等通過引入電離層延遲先驗信息，將電離層延遲作為未知參數(shù)與位置參數(shù)以及模糊度參數(shù)一并求解，提高了單歷元模糊度固定成功率[8]。梁宵等針對TCAR和CIR在模糊度解算性能上弱于最小二乘降相關(guān)平差法(Least-squares AMBiguity Decorrelation Adjustment, LAMBDA)的問題，提出了一種寬窄巷結(jié)合的LAMBDA整周模糊度解法，并獲得了毫米級的相對定位精度[9]。王官龍等提出了一種北斗三頻無故障導航算法，并將其運用于海基精密進近與著陸系統(tǒng)(Joint Precision Approach and Landing System, JPALS)中，能夠在短時間內(nèi)實現(xiàn)模糊度的正確固定[10]。

TCAR主要可以分為幾何(Geometry-Based，GB)和無幾何(Geometry-Free，GF)兩種模式，在短基線條件下，電離層延遲誤差通過雙差幾乎完全消除，觀測噪聲和多路徑誤差成為主要誤差源[11]。在動對動情形下，偽距觀測噪聲過大將會導致模糊度解算不可靠。因此，偽距測量精度是影響模糊度固定的決定性因素。

慣性/衛(wèi)星組合導航系統(tǒng)能夠持續(xù)提供高精度位置輸出，其誤差不隨時間累積，且其工作過程不受外界測量環(huán)境影響，能夠有效避免觀測噪聲和多路徑誤差的影響[12]。肖凱等首次提出了基于GNSS/INS緊組合的三頻整周模糊度解法，獲得了高精度的組合導航解[13]，但是該算法的核心是實現(xiàn)組合導航，而不是進行動態(tài)相對定位。本文在BDS/INS緊組合的基礎(chǔ)上，提出了一種適用于動對動情形的三頻整周模糊度解算方法。

1 算法設(shè)計

本文旨在研究動對動條件下的整周模糊度解算方法，無固定基準站作為參考，故在兩個運載體上各自配備一套組合導航系統(tǒng)，兩套系統(tǒng)獨立工作。傳統(tǒng)TCAR第一步采用偽距觀測值來估算超寬巷模糊度，但由于動對動條件下偽距測量值容易產(chǎn)生粗差或者多路徑效應，導致其誤差較大，從而使得超寬巷模糊度的解算可靠性下降。因此本文采用BDS/INS緊組合的實時位置輸出代替?zhèn)尉嘤^測值，在GF和GB兩種模式下分別進行組合模糊度解算，并恢復初始模糊度。具體算法框圖如圖1所示。

圖1 三頻整周模糊度解算框圖Fig.1 Triple-frequency integer ambiguity calculating block diagram

2 BDS/INS緊組合模型

BDS/INS緊組合模型采用偽距組合方式[14]。

誤差狀態(tài)方程可以表示為：

(1)

觀測方程由BDS測量得到的偽距與INS推算的偽距作差得到

(2)

3 三頻整周模糊度解算

在選取組合模糊度時首先要求組合系數(shù)是整數(shù)，以保持模糊度的整數(shù)特性，此外還需盡量滿足組合波長長、電離層延遲小和噪聲放大因子小的要求。在短基線條件下，電離層延遲誤差可以忽略不計，此時主要考慮組合波長長、噪聲放大因子小的組合。根據(jù)文獻[11]的分析，本文選取(0，1，-1)、(1，0，-1)和(1，0，0)依次作為超寬巷(Extra Wide Lane, EWL)、寬巷(Wide Lane, WL)和窄巷(Narrow Lane, NL)的組合系數(shù)。

3.1 geometry-free模式

傳統(tǒng)無幾何模式下的TCAR算法利用偽距雙差觀測值來估計EWL整周模糊度。短基線條件下，組合系數(shù)為(0，1，-1)的雙差整周模糊度通過下式直接取整得到。

ΔN(0,1,-1)=Δ

(3)

ΔN(1,0,-1)=Δφ(1,0,-1)-

(4)

ΔN(1,0,0)=Δφ(1,0,0)-

(5)

當以上三個組合整周模糊度被依次確定后，另外兩個雙差原始整周模糊度ΔN(0,1,0)和ΔN(0,0,1)也可以被正確求解。

根據(jù)誤差傳播理論，假設(shè)載波相位觀測噪聲與偽距觀測噪聲互不相關(guān)[15]，則式(3)～(5)中由觀測噪聲引起的組合整周模糊度誤差均方差分別為：

(6)

(7)

(8)

由式(6)～(8)易知，EWL模糊度解算同時受到載波相位噪聲和偽距噪聲的影響，而WL和NL模糊度解算只受載波相位噪聲的影響。由于載波相位測量精度與多路徑效應以及接收機靈敏度等因素有關(guān)，很難通過有效手段對其進行顯著提高，因此本文著重分析偽距誤差對模糊度解算的影響。假設(shè)北斗非差載波相位觀測值噪聲標準差為0.02周，則雙差載波相位觀測值噪聲標準差為0.04周。對于式(3)來說，利用四舍五入取整法成功解算EWL整周模糊度的前提條件為：

|dΔN(0,1,-1)|<0.5

(9)

根據(jù)“3σ”原則，按照99.74%置信區(qū)間，取

(10)

則

σ<0.814

(11)

σρ<0.407

(12)

即要求動對動條件下的偽距觀測值均方誤差不超過0.407 m。而在復雜觀測條件下偽距測量誤差的增大極有可能導致EWL整周模糊度固定錯誤。故本文采用BDS/INS緊組合對無幾何模式下的TCAR算法進行改進。利用BDS/INS緊組合偽距更新得到的接收機實時高精度位置坐標推算接收機到衛(wèi)星的幾何距離，并用其代替?zhèn)尉嘤^測值，從而式(3)改寫為：

(13)

3.2 geometry-based模式

幾何模式下的TCAR算法與無幾何模式下的區(qū)別在于，逐級解算模糊度時不再采用直接取整的無幾何模型，而是采用幾何模型來求解。其具體步驟如下。

步驟1：采用最小二乘法解算EWL的模糊度浮點解

(14)

步驟2：采用最小二乘法解算WL的模糊度浮點解

(15)

其中

Δφ(0,1,-1)-ΔN(0,1,-1))

(16)

同樣地，在得到WL的模糊度浮點解及其協(xié)方差矩陣后，利用LAMBDA算法即可得到WL模糊度固定解。

步驟3：采用最小二乘法解算NL的模糊度浮點解

(17)

其中：

Δφ(1,0,-1)-ΔN(1,0,-1))

(18)

得到NL的模糊度浮點解及其協(xié)方差矩陣后，利用LAMBDA算法即可得到NL模糊度固定解，最后還原初始模糊度。

考慮到偽距觀測值噪聲的影響，本文采用改進的GB-TCAR算法，在解算EWL模糊度浮點解時，將雙差偽距觀測值用緊組合系統(tǒng)推出的雙差幾何距離Δρc代替，則式(14)改為：

(19)

其余步驟保持不變。

4 算例分析

本文的實驗數(shù)據(jù)通過仿真產(chǎn)生。為了驗證動對動條件下的算法性能，按如下步驟進行實驗數(shù)據(jù)的仿真。

步驟1：仿真產(chǎn)生兩段飛機編隊飛行軌跡，總時長為1200 s，兩段軌跡的初始位置均為東經(jīng)108.54°、北緯34.15°，高度相差100 m，且在飛行過程中始終保持100 m不變。因此，在飛行過程中兩架飛機之間形成的基線長度始終為100 m。同時產(chǎn)生兩段相應的慣導跟蹤軌跡，兩個慣導的精度水平一致，陀螺儀漂移誤差設(shè)置為0.01 (°)/h，加速度計零偏誤差設(shè)置為10μg。

步驟2：利用衛(wèi)星星座模擬器產(chǎn)生一段時間的衛(wèi)星星歷數(shù)據(jù)，從而得到該段時間內(nèi)兩架飛機的偽距觀測值和載波相位觀測值。

步驟3：利用前文介紹的BDS/INS緊組合模型對步驟1和步驟2中的仿真慣導數(shù)據(jù)和偽距觀測數(shù)據(jù)進行組合處理，得到組合位置輸出值。

4.1 BDS/INS緊組合模型性能仿真分析

對BDS/INS緊組合模型在不同偽距噪聲水平下的導航定位性能進行仿真，其輸出的位置誤差如圖2所示，位置誤差均方差如表1所示。

(a) x方向誤差(a) Errors in x direction

(b) y方向誤差(b) Errors in y direction

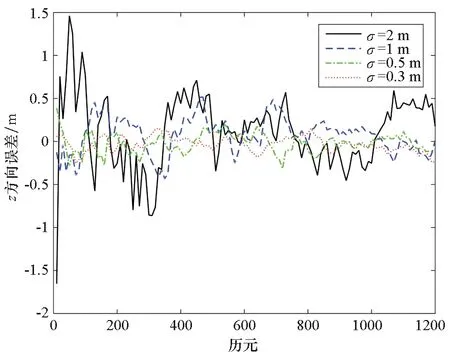
(c) z方向誤差(c) Errors in z direction圖2 BDS/INS緊組合模型位置誤差Fig.2 BDS/INS tightly-coupled model positioning error

表1 BDS/INS緊組合模型位置誤差均方差

從圖2和表1可以看出，當偽距噪聲標準差在2 m以內(nèi)時，該緊組合模型輸出的x、y、z三個方向的位置精度能夠達到分米級甚至厘米級，利用該位置推算出的幾何距離均方誤差不超過0.628 2 m，其精度相比于原始偽距觀測值提升了60%以上，因而能夠被用來替代偽距觀測值進行整周模糊度的解算。

4.2 三頻整周模糊度解算性能仿真分析

為了驗證本文所提算法的模糊度解算性能，分別采用GF、GB、BDS/INS緊組合輔助的無幾何模式(TC+GF)以及BDS/INS緊組合輔助的幾何模式(TC+GB)在相同載波相位噪聲水平(設(shè)為0.02周)、不同偽距噪聲水平條件下對三頻整周模糊度進行逐級解算，并對其模糊度解算成功率進行比較分析。為了使所得結(jié)論更加具有普遍性和說服力，對每個實驗程序均重復運行1000次，取其算術(shù)平均值作為實驗結(jié)果，如表2所示。

從表2可以看出：GB模式下的整周模糊度解算成功率高于GF模式，這是由于幾何模型充分運用了所有可見衛(wèi)星的觀測信息，有效提高了模糊度浮點解精度，并采用了LAMBDA算法對模糊度浮點解進行了搜索和固定；在偽距觀測噪聲標準差為1 m以上時，GF模式下的模糊度解算成功率不足25%，GB模式下的模糊度解算成功率不足80%，而加入BDS/INS緊組合輔助后，各級模糊度解算成功率均在99%以上，模糊度解算成功率顯著提高。此外，在BDS/INS緊組合輔助的GB模式下，當偽距觀測噪聲標準差不超過1 m時，各級模糊度解算成功率均達到了100%。GF模式下超寬巷、寬巷和窄巷模糊度解算成功率逐漸降低，這是由于下一級模糊度解算與上一級有關(guān)，并且下一級模糊度解算時加入了新的觀測噪聲，而GB模式使用了LAMBDA算法，一定程度上削弱了觀測噪聲對于下一級模糊度解算的影響，使得三者的解算成功率基本相當。

在偽距觀測噪聲標準差為1 m時，利用BDS/INS緊組合輔助的GB模式進行兩個運載體之間的基線矢量解算，基線長度及其誤差如圖3所示，基線矢量x、y、z方向誤差如圖4所示。從圖中可以看出，基線長度誤差均在5 cm以內(nèi)，基線矢量在x、y、z方向上的誤差也均在5 cm以內(nèi)。這表明該方法能夠?qū)崿F(xiàn)厘米級的動對動相對定位。

圖3 基線長度及其誤差Fig.3 Baseline length and error

表2 三頻整周模糊度解算成功率

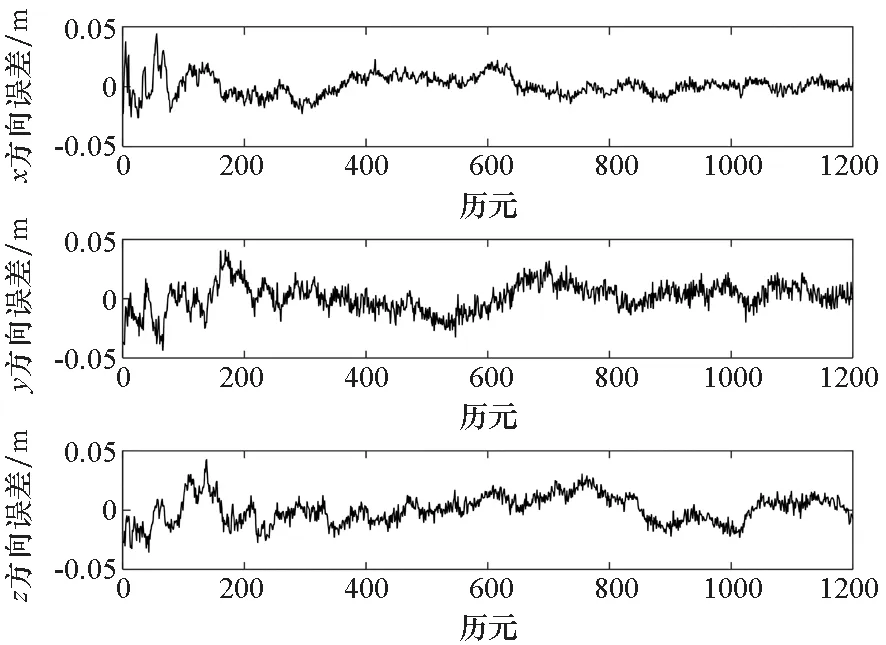
圖4 基線矢量x、y、z方向誤差Fig.4 Baseline vector errors in x、y and z directions

5 結(jié)論

本文提出了一種BDS/INS緊組合輔助的動對動三頻整周模糊度解算方法，通過緊組合輸出的高精度實時位置坐標推算出雙差幾何距離，并用其代替原始TCAR算法中的雙差偽距觀測值，分別在GF和GB兩種模式下分析其模糊度解算性能。仿真結(jié)果表明，在BDS/INS緊組合的輔助下，三頻整周模糊度的解算成功率顯著提高，當偽距觀測噪聲標準差不超過2 m時，兩種模式下的模糊度解算成功率均在99%以上。由于在解算模糊度之前首先需要對BDS和INS的數(shù)據(jù)進行緊組合處理，模糊度解算的實時性有待進一步研究。