線性經濟模型換基迭代準則的研究
李永平
(天津財經大學理工學院,天津 300222)
一、引言
資源優化配置模型是經濟優化決策的核心問題,也是決策的關鍵所在,特別是線性經濟模型由于其結構簡單、經濟意義明晰、算法相對成熟,因此作為管理科學的基礎理論—線性規劃技術在實踐中得以廣泛應用。
對資源優化配置的線性經濟模型,G.B.Dantzig的單純形方法(Simplex method)在實踐中證明是非常有效和普遍適用的,其基本的思想方法與步驟分為兩個階段:其一是尋找初始基可行解,對其進行最優性的判別,若是,則求解結束;否則,轉入第二個階段即換基迭代,得到使目標函數改進的下一個基可行解,對此基可行解置其為初始基可行解,即回到第一個階段;如此循環,有限步迭代之后一定可以得到問題的最優解(或判定無最優解)。但在具體的換基迭代過程中,其進基變量的選擇,通常選擇檢驗數所對應的基變量xj為進基變量,這樣的選擇,一定可以使目標函數f 得以改進(特別是在非退化情形下,f的改進是嚴格增加的;在退化的情形下,它至少是不減的)。但我們經過認真研究發現它并不是當前狀態下的最好的選擇,在換基迭代時,如果在考慮λj的同時一并考慮xj的調整量θj,則可使目標函數得到更好的改進(即增加值更大),從而使迭代步驟有效減少,這一點,對大型的線性經濟模型問題,有著十分重要的意義;同時,對一類退化的線性經濟決策模型,可以避免迭代循環現象的發生。
二、問題及相關命題
(一)線性經濟模型
一般地,在標準化意義下,基于資源優化配置的線性經濟模型表述為:

其中,c=(c1,c2,…,cn),x=(x1,x2,…,xn)T
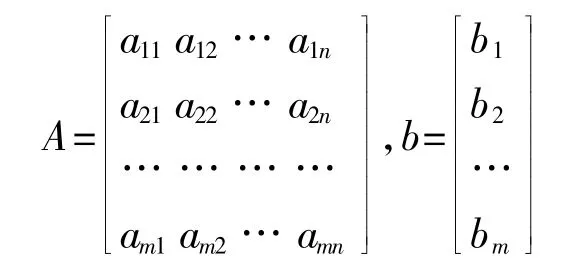
這里f 是目標函數,Am×n為技術系數矩陣,b 為可利用的資源數量,c 為產品的價格向量,且約定矩陣Am×n行滿秩,以表明產品生產的m 種資源約束均為有效約束。
(二)典式及單純形表



定理3 所表述的實際是問題(1)的換基迭代具體算法,在經過以上步驟后,實現了從可行基x0到可行基x1的轉換。
在具體的模型求解中,為方便過程敘述與求解,將定理1、定理2、定理3 就基可解的判別、換基迭代等過程,歸納總結列于表當中,也就是通常說的單純形(Dantzig)表。在具體計算過程中,當出現兩個或兩個以上的檢驗數λj>0 的情形,以往迭代的一般做法是:取其中最大的檢驗數λm+k[3]67:


由此,{p1,p2,…,pl-1,pl,pl+1,…,pm}向量組可由{p1,p2,…,pl-1,pm+k,pl+1,…,pm}向量組線性表示,另B為基陣,向量組{p1,p2,…,pl-1,pm+k,pl+1,…,pm}自然可由向量組{p1,p2,…,pl-1,pl,pl+1,…,pm}線性表示,因此兩向量組可相互表示,為等價關系,由定理:等價向量組有相同的秩,{p1,p2,…,pl-1,pm+k,pl+1,…,pm}線性無關得證。
由所證第一、第二,參考定理3 的證明[1]30-33易得定理4。
需要指出的是:定理4 在實現一個基可行解到另一個基可行解迭代的同時,實現了當前狀態下目標函數最大的增加值,是最優步長選擇的迭代,較過去換基迭代方法減少一些迭代步驟,特別是當面臨較大型的資源配置線性經濟模型時,其優越性更加凸顯;同時,在模型(1)的基可行解是退化情形下,可以避免原來換基迭代方法出現的循環情形。
三、算例分析
例1:求解下列問題:
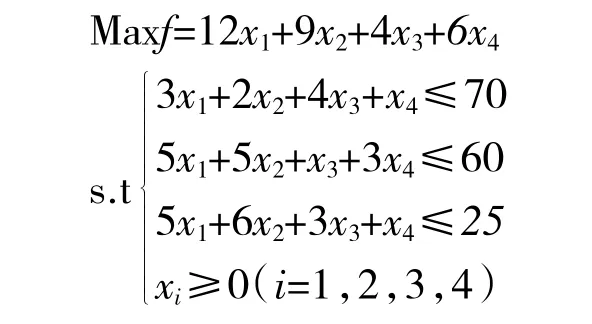
解:引入松弛變量,將問題標準化,易得第一張單純形表(見表1)。
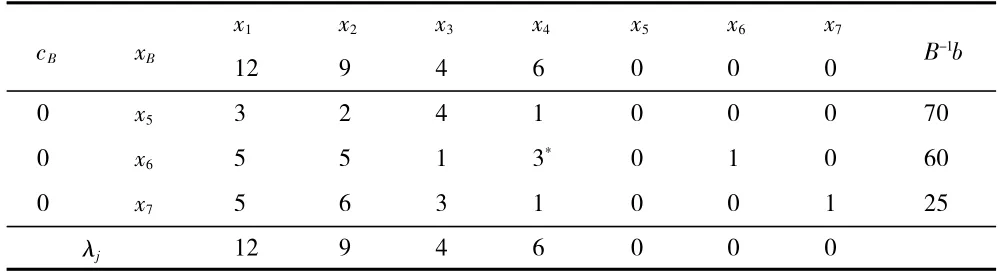
表1


表2
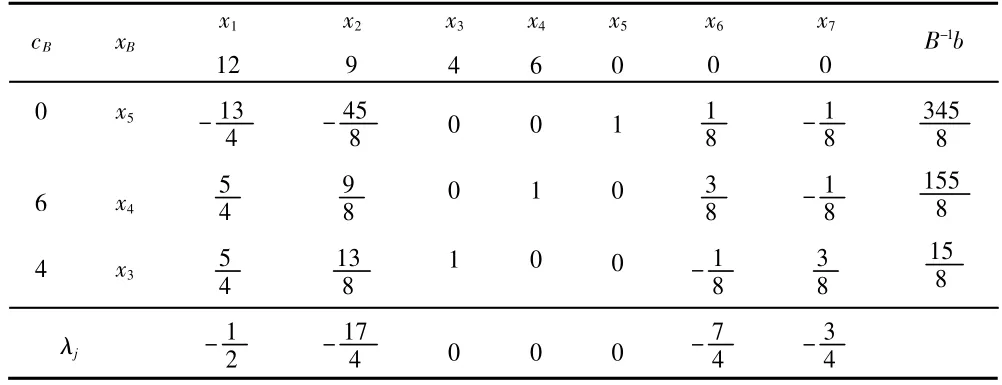
表3
由表3 可知原問題的最優解是:
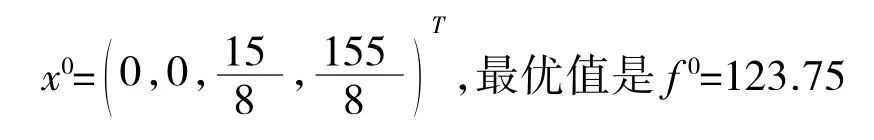
它經過3 次換基迭代,而如果按原來的做法,則需要4 次換基迭代(因篇幅所限,具體做法這里略去)。
下面再舉一例,這是1955 年,由著名數學家E.Beale 所提出的一個退化的、換基迭代出現循環的線性經濟模型的經典范例。
例2:求x1,x2,…,x7滿足:

在這個例中,有一個明顯的可行基{x5,x6,x7},而且這是一個退化的可行基,從這個基開始進行迭代,在迭代過程中,當有幾個λj同時是正時,選λj絕對值較大的列對應的變量作為換入變量。如果有幾個基變量同時使θ 達到最小,就取下標較小的那一個作為換出變量。可以發現經過6 次迭代后,又得到了最初的可行基{x5,x6,x7},即出現循環,這樣下去永遠不會得到最優解[1]53-56。它表明對退化的線性經濟模型問題用定理3 的方法進行迭代計算,有可能因出現循環而得不到結論。當然,避免循環以求解線性經濟模型有攝動法和字典序方法,這里,針對例2采用定理4 之方法就可以避免其出現循環,且只需迭代2 次即得最優解。具體迭代過程,列于表4、表5、表6 中(表中帶星號的數是迭代選定的樞紐元素)。
由表6 可得:例2 的最優解為:
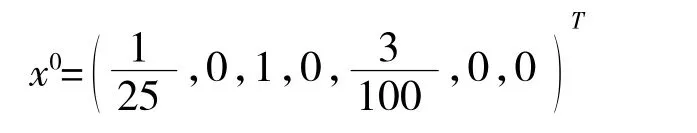
最優值為:
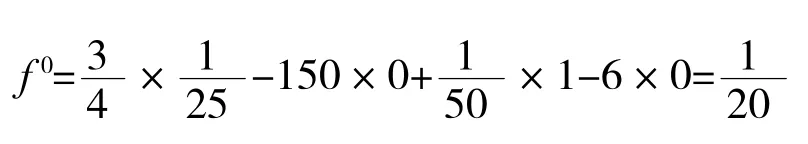
四、結論與展望
以上我們討論了有關資源配置的線性經濟模型Dantzig 的換基迭代算法,并作了一點的改進,通過實例計算它是有效的。但就算法而言,由于面臨現實問題的復雜性、多樣性與特殊性,任何一種算法都只能是相對有效的,表現為“此優彼劣”,不可能“一勞永逸”解決所有的問題。“沒有最好,只有更好”,在此,我們拋磚引玉期待有更好的算法以豐富與完善線性規劃技術,為經濟優化決策、為經濟過程的定量化分析提供更有效也更有力的工具。

表4
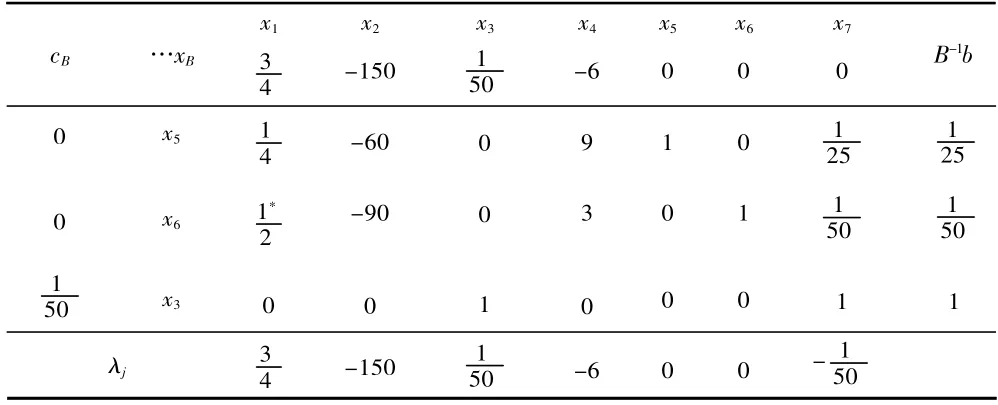
表5
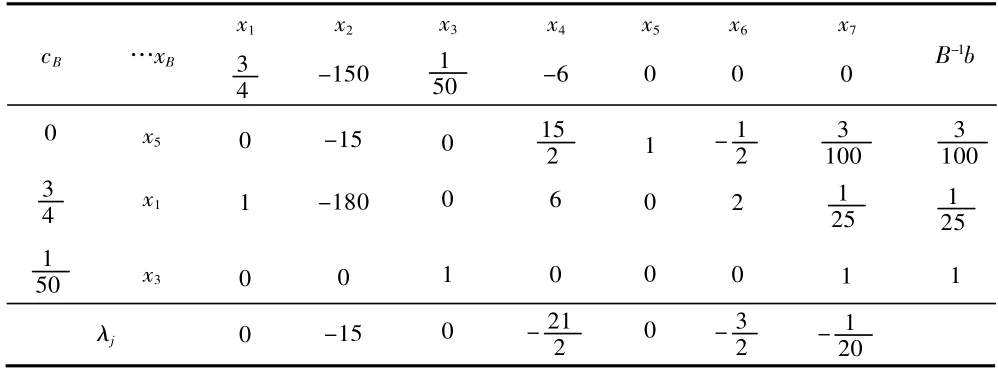
表6

