北斗工程IGSO/MEO/GEO發射軌道設計

周天帥，周 桃，張亦樸，張博俊

(北京宇航系統工程研究所，北京 100076)

0 引言

北斗衛星導航系統(Beidou navigation sate-llite system)是我國自行研制的全球衛星導航系統[1]。系統建設采取了“三步走”戰略，經歷北斗一號、二號、三號系統，實現從定位試驗系統到全球導航定位系統的跨越式發展[2]，北斗三號系統已于2020年6月全面建成[3]。

北斗工程有3類衛星：傾斜地球同步軌道(Inclined Geosynchronous Orbit， IGSO)、中地球軌道(Medium Earth Orbit，MEO)和地球同步軌道(Geostationary Earth Orbit，GEO)衛星[4-7]。對應軌道如下：北斗一號工程僅有地球同步轉移軌道(Geostationary Transfer Orbit, GTO)，由CZ-3A火箭發射。北斗二號工程衛星對應的發射軌道分別為：傾斜同步轉移軌道( Inclined Geostationary Transfer Orbit，IGTO)、中圓轉移軌道(Medium Transfer Orbit，MTO)和GTO；IGTO和MTO軌道傾角均為55°，由CZ-3A和CZ-3B火箭發射；GTO軌道采用我國第一個非軸對稱火箭——CZ-3C火箭發射。北斗三號工程的IGSO衛星和GEO衛星均采用了GTO軌道，由CZ-3B火箭發射，MEO衛星均由CZ-3B+YZ-1上面級一箭雙星發射，CZ-3B火箭取消末修和調姿段，將上面級+衛星組合體送入近MTO軌道，后續由上面級兩次變軌將衛星送入MEO軌道。由此可見，CZ-3A系列火箭承擔了北斗工程全部發射任務[8]。

北斗工程對CZ-3A系列火箭發射軌道要求見表1，本文不涉及YZ-1上面級段軌道設計及要求。

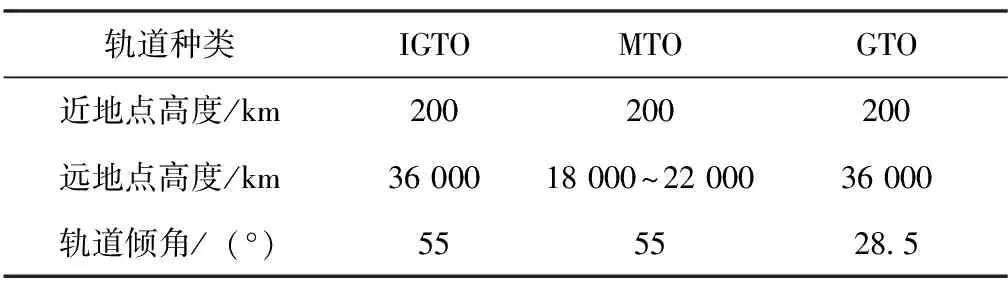
表1 北斗工程對CZ-3A系列火箭軌道要求

本文討論上述軌道要求下火箭飛行方案、發射軌道設計及高空風雙向補償方法。

1 北斗工程火箭飛行方案

1.1 IGTO/MTO軌道發射方案

針對IGTO/MTO的軌道要求，經過研究及各大系統間協調，確定了如下發射軌道方案：

1)采用新的東南射向進行IGTO/MTO軌道發射；若仍采用以往104°(CZ-3A火箭)或97.5°(CZ-3B和CZ-3C火箭)射向，則需要增加較大的偏航程序角才能滿足軌道傾角要求，但運載能力顯著降低，無法滿足衛星質量要求。

2)引入三檔典型設計風場，采用變射向高空風雙向補償方案進行發射軌道設計；北斗工程發射任務多，執行任務月份很多在西昌地區高空風較大的季節，在新的射向下，必須采取高空風雙向補償措施。

3)受地面瞄準間條件限制，需采用地面固定射向瞄準、起飛后滾轉定向方案，發射軌道設計中綜合考慮了火箭安全出塔和程序轉彎時間，設計了起飛滾轉程序角。

4)采用三級連續推進入軌的發射軌道方案；在北斗工程立項論證早期，曾使用三級兩次工作的模式，但發射軌道設計的星箭分離點位于澳大利亞中部上空，在澳大利亞領海外布設測量船都無法跟蹤星箭分離，而在其領土內設站亦有很大困難，為此，提出三級連續工作入軌方案，取消滑行時間放寬對近地點幅角約束，將入軌航程由8 000 km減小到4 000 km，帶來的好處是僅需一艘測量船即可完成入軌段的測控任務。

1.2 GTO軌道發射方案

北斗工程發射GTO軌道采用東射向(97.5°)，三級二次工作入軌方案，先后分別采用CZ-3C和CZ-3B火箭發射。

其中北斗二號工程階段該軌道采用的運載火箭為我國第一枚非軸對稱構型火箭——CZ-3C火箭，有別于以往GTO軌道發射采用的軸對稱火箭。需開展基于非軸對稱火箭GTO軌道設計：在其助推器飛行段，俯仰、偏航兩個通道氣動特性不對稱。根據其不對稱性，引入了俯仰、偏航兩個通道不同氣動力系數，進行彈道尋優設計計算。

2 IGTO/MTO發射軌道設計

2.1 采用新的東南射向

為滿足衛星對運載能力及衛星軌道傾角要求，確定采用新的東南射向進行設計。136.5°射向開辟新的落區。航區經過的大城市相對原來的近東射向有所變化，圖1給出了航區箭下點軌跡示意圖。

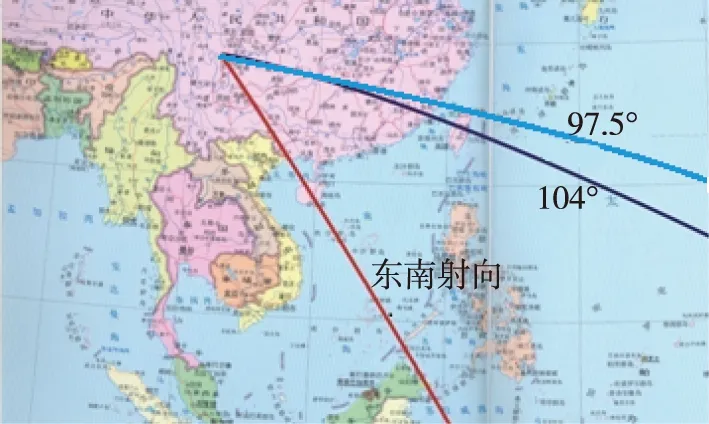
圖1 航區箭下點軌跡示意圖Fig.1 Trajectory of Launch Vehicle

2.2 對CZ-3A系列火箭發射軌道要求

衛星對CZ-3A火箭發射軌道設計的要求，主要來自衛星和火箭控制系統，還有地面測控系統對火箭航區的要求以及子級落區的限制等，主要包括：

1)衛星入軌點密切橢圓軌道的近地點高度Hp、遠地點高度Ha、軌道傾角i、近地點幅角ω；

2)衛星入軌點姿態參數；

3)控制系統對火箭姿態角、姿態角速率的限制和發動機啟動、關機前后姿態保持的要求；

4)地面測控系統對火箭航程的限制；

5)子級殘骸落區對火箭射向和子級射程的限制。

2.3 發射軌道優化目標與優化控制參數選擇

CZ-3A系列火箭發射軌道優化設計的目標是使衛星入軌時火箭三級推進劑剩余量最大，這個目標與火箭運載能力最大是等價的。

有下列7個節點的俯仰程序角作為火箭軌道設計及優化的控制參數，即：

1)一、二級分離前后俯仰程序角φcxk1；

2)二級起始程序角快速變化段結束時俯仰程序角φcx21；

3)二、三級分離前后俯仰程序角φcxk2；

4)三級起始程序角快速變化段結束時俯仰程序角φcx31；

5)三級程序角勻速變化段第一段結束時俯仰程序角φcx32；

6)三級程序角勻速變化第二段結束時俯仰程序角φcx33；

7)三級關機前后俯仰程序角φcxk3。

在CZ-3A系列火箭發射IGTO/MTO轉移軌道設計中，由于采用了高空風雙向補償技術，在火箭一級飛行段加入了偏航程序，二級飛行段及三級飛行段開始的前30 s，偏航程序保持一二級分離時的偏航程序不變。從30 s開始至40 s繼續加入偏航程序，40 s時的偏航程序角ψcx3作為火箭軌道設計的控制參數。

此外，火箭三級發動機的關機時間tk3也可以作為火箭軌道設計的控制參數。這樣，CZ-3A系列火箭發射IGTO/MTO轉移軌道優化設計的控制參數為9個。

2.4 發射軌道優化中約束的處理方法

發射軌道優化中對于指定終端條件和子級落點的約束，首先以迭代的方式使其得到精確滿足。迭代過程中具體使用的參數如下：

1)對火箭一子級殘骸落點的射程約束，通過迭代方法對火箭一、二級分離前后俯仰程序角φcxk1進行調整，使其得到滿足；

2)對火箭二子級殘骸落點的射程約束，通過迭代方法對火箭二、三級分離前后俯仰程序角φcxk2進行調整，使其得到滿足；

3)衛星給定的入軌點密切橢圓軌道遠地點高度Ha(或軌道半長軸a)終端約束，通過迭代方法對火箭三級關機時間tk3進行調整，使其得到滿足；

4)衛星給定的入軌點密切橢圓軌道近地點高度Hp和近地點幅角ω這兩個終端約束，通過迭代對火箭三級程序角勻速變化第一段結束時俯仰程序角φcx32和三級關機前后俯仰程序角φcxk3進行調整，使它們得到滿足；

5)衛星給定的入軌點密切橢圓軌道傾角i終端約束，通過迭代方法對三級偏航程序角ψcx3進行調整，使其得到滿足。

其余3個參數可采用常用的直接優化尋優方法參與優化。

2.5 高空風雙向補償技術

我國西昌地區上空處于西風帶，高空風多為西風。此前，我國火箭僅有單向風補償設計。CZ-3A和CZ-3B火箭從西昌衛星發射IGTO/MTO任務沿136.5°射向發射，高空風在垂直于射面的橫向分量與射面內的縱向分量相當，這時，只對射面內的縱向風進行補償，不能有效降低火箭飛行中受到的風載荷。為滿足CZ-3A系列火箭發射放行的qα(最大載荷系數)要求，必須減小飛行中高空風引起的氣動攻角，需要解決高空風雙向補償問題。

具體的技術方案描述如下：

1)在進行高空風雙向補償設計時，通過調整射向來消除火箭一子級殘骸落點橫向偏差。

2)在標準彈道設計時預先引入設計風場，根據設計風場進行高空風雙向補償彈道的俯仰程序角和偏航程序角設計。為增加發射覆蓋率，需在統計風場基礎上，對高空風場進行分檔，形成不同的設計風場，通過迭代選擇滿足火箭一子級殘骸落點射程要求的補償彈道，并依據預先確定的火箭子級殘骸落區位置調整火箭射向。

3)從風補償結束直至三級飛行開始，火箭偏航程序角一直都與風補償結束時保持相同，只在三級飛行30 s后才繼續改變火箭偏航程序角，以達到衛星入軌要求的軌道傾角。這不僅使火箭各子級殘骸落點位置基本不受風補償的影響，而且火箭運載能力也沒有因風補償而受到損失。同時，由于火箭控制裝訂諸元，都是針對雙向補償彈道設計計算的，與不進行風補償比較，火箭飛行中受到的風干擾，由實際高空風變為實際高空風相對所采用設計風場的偏差，在火箭參數偏差和飛行中受到的其他干擾不變情況下，衛星入軌精度應略有提高，不會因風補償而受到不利影響。

2.5.1 設計風場的確定

CZ-3A系列火箭發射IGTO/MTO軌道，以2月份95%概率統計風場為基礎，將風速分別乘以系數0.25，0.5和0.75，而風向不變，生成了三檔典型設計風場，此三檔設計風場基本可以覆蓋全年大部分月份。針對三檔設計風場相應設計了3條雙向風補償程序。

2.5.2 高空風雙向補償設計結果及實施效果

CZ-3A火箭三檔高空風雙向補償下一級俯仰程序角FICX和偏航程序角PSCX設計結果如圖2所示。

圖中 1代表一檔25%雙向風補償程序，2代表二檔50%雙向風補償程序，3代表三檔75%雙向風補償程序。在進行風補償計算時，如果得到的qα值超過火箭結構強度對qα的限制值，則認為火箭在此風補償方式下不能滿足火箭發射放行條件。

以CZ-3A 火箭發射MEO衛星任務中采用50%風補償程序作為最終上天飛行程序為例，根據飛行中的遙測數據及射后半小時實測高空風數據進行擬合計算，補償效果如圖3所示。

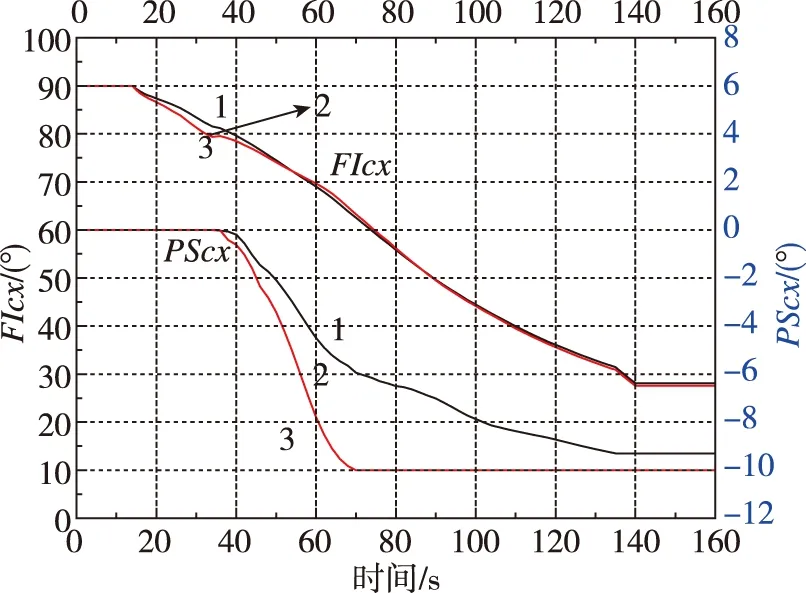
圖2 CZ-3A三檔雙向補償俯仰程序角和偏航程序角Fig.2 Pitch and yaw program angles of CZ-3A in three-gear compensation

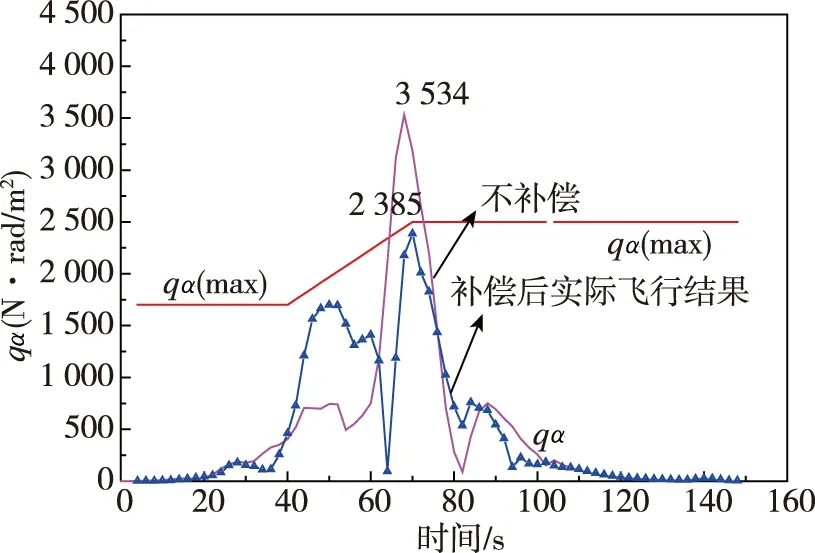
圖3 實際飛行中的qα值和不補償qα值曲線Fig.3 The qα curves of actual flight and no wind compensation

從圖3可以看出，若不采取高空風雙向補償方案，飛行中最大qα值可達3 534 Pa·rad，超過了qα限制線(紅色線)，火箭將不能按時發射。而采用高空風雙向補償技術方案后，實際飛行中出現的最大載荷系數為2 385 Pa·rad，滿足發射放行條件。高空風雙向補償技術的應用確保了發射計劃的按時完成。

3 GTO發射軌道設計

北斗二期工程發射GTO軌道首次采用CZ-3C運載火箭，有別于以往GTO軌道發射采用的火箭，它是我國第一枚非軸對稱構型大型液體運載火箭。

優化過程與傳統軸對稱火箭發射GTO設計方法沒有區別。區別在于軸對稱火箭氣動法向力系數導數和側向力系數導數相同，而CZ-3C火箭助推飛行段全箭氣動法向力系數導數和側向力系數導數、壓心系數及姿控系統偏航、俯仰通道靜態放大系數存在差異。

根據其不對稱性，引入了俯仰、偏航兩個通道不同氣動力系數，進行彈道設計計算。下面詳細介紹非軸對稱相對傳統軸對稱設計引起差異的問題。

與軸對稱火箭側向力系數等于法向力系數處理方式的計算結果差異主要體現在風補償計算和參數差異對偏差彈道影響。

3.1 風補償計算

火箭發射前需完成風補償程序生成和qα計算。非軸對稱和軸對稱計算的差異較大，α為復合攻角，是攻角和側滑角的綜合值。非軸對稱火箭風干擾下的側滑角β可用以下公式計算[9-10]

(Δψw-σ+βw)=Aψ(Δψw-σ+βw)

式中，Δψw為偏航角地球旋轉修正量，σ為彈道偏角，βw為側風產生側滑角。軸對稱火箭以Aψ等于Aφ計算。為分析以Aψ等于Aφ造成的非軸對稱火箭側滑角β+βw的計算誤差，應用側向力系數導數、側向壓心系數與偏航通道放大系數，以上述公式計算出CZ-3C火箭助推飛行段的側向系數Aψ(AFIB)，又用法向力系數導數、法向壓心系數和俯仰通道放大系數以同樣公式計算出法向系數Aφ(AFI)，以Aψ等于Aφ引起的相對偏差為(AFI-AFIB)/AFIB，計算結果如圖4所示。

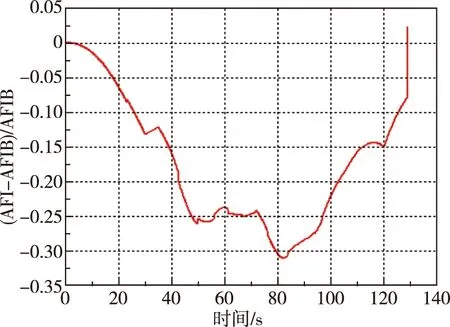
圖4 以Aψ等于Aφ引起的相對偏差變化情況Fig.4 Aφ instead of Aψ caused change in relation deviation

由于側滑角β+βw與Aψ成比例，因此以Aψ等于Aφ造成的側滑角β+βw的相對誤差，如圖4中的(AFI-AFIB)/AFIB表示。通常在大風區40～70 s時qα值出現最大值。從圖4可看出，40～70 s飛行段，非軸對稱火箭如果以代替Aψ等于Aφ計算側滑角β+βw約有-25%～30%的誤差。

3.2 參數差異對偏差彈道影響

以上參數差異主要對橫向彈道參數偏差產生影響，其中發射坐標系橫向坐標偏差DZ和實時落點緯度偏差DB與傳統軸對稱火箭計算的偏差彈道計算中列出數據DZ′和DB′的比值隨時間變化情況如圖5、圖6所示。

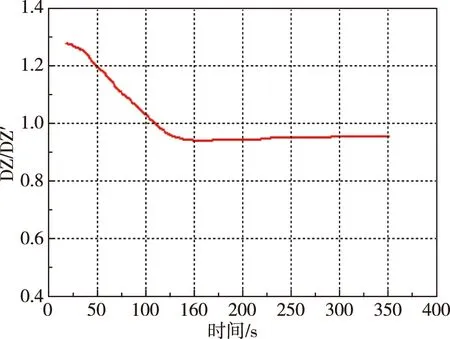
圖5 橫向坐標偏差比值DZ/DZ′Fig.5 Transverse coordinate deviation ratio of DZ/DZ′

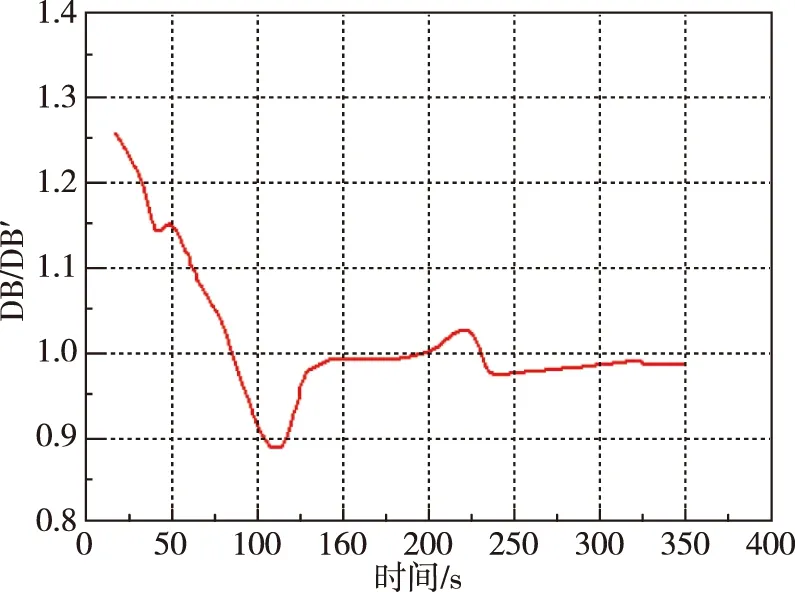
圖6 實時落點緯度偏差比值DB/DB′Fig.6 Real-time latitude deviation ratio of DB/DB′

從圖5可以看出，在110 s前，橫向坐標偏差新計算結果DZ要比按傳統軸對稱處理方式計算的相應偏差DZ′大，最大倍數為1.27倍；110 s后則相反，兩者偏差比值小于1。

從圖6可以看出，在84 s前，非軸對稱處理方式計算的落點緯度偏差計算結果DB要比軸對稱處理方式提供結果DB′大，最大倍數為1.26倍；200～230 s間雖然也大，但差距較小，最大倍數才1.026，其他時間段兩者偏差比值則小于等于1。

CZ-3C火箭發射成功充分驗證了非軸對稱火箭發射GTO軌道設計的正確性。

4 結論

本文針對IGSO/MEO/GEO衛星發射方案、軌道設計方法進行了介紹。該方法有效增加CZ-3A系列火箭對發射任務的適應能力，大大增加火箭按時發射概率和火箭飛行安全性，對我國北斗導航工程的按時實施提供了必要的技術基礎。