4t?1 元旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的構(gòu)造

杜蛟，劉春紅，龐善起

（1.河南師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，河南 新鄉(xiāng) 453007；2.河南師范大學(xué)大數(shù)據(jù)統(tǒng)計(jì)與優(yōu)化控制河南省工程實(shí)驗(yàn)室，河南 新鄉(xiāng) 453007；3.河南師范大學(xué)計(jì)算機(jī)與信息工程學(xué)院，河南 新鄉(xiāng) 453007）

1 引言

文獻(xiàn)[2-3]首先研究了具有相關(guān)免疫性和高非線性度的旋轉(zhuǎn)對(duì)稱布爾函數(shù)；文獻(xiàn)[9-11]研究了平衡的旋轉(zhuǎn)對(duì)稱布爾函數(shù)以及相關(guān)免疫旋轉(zhuǎn)對(duì)稱布爾函數(shù)的構(gòu)造與計(jì)數(shù)問題；文獻(xiàn)[12]研究了相關(guān)免疫階的判別問題；文獻(xiàn)[13-17]研究了旋轉(zhuǎn)對(duì)稱1-彈性函數(shù)的若干具體構(gòu)造方法；文獻(xiàn)[18]給出了一個(gè)旋轉(zhuǎn)對(duì)稱彈性函數(shù)的二級(jí)構(gòu)造方法，但是該方法依賴于已有的低階彈性旋轉(zhuǎn)對(duì)稱函數(shù)，構(gòu)造的函數(shù)的變?cè)獋€(gè)數(shù)局限性較大；文獻(xiàn)[19-20]進(jìn)一步將旋轉(zhuǎn)對(duì)稱彈性函數(shù)的構(gòu)造問題從特征為 2 的有限域上推廣到特征為奇素?cái)?shù)的有限域上。基于以上結(jié)果，本文基于軌道交換方法給出了一類具有4t?1 個(gè)變?cè)男D(zhuǎn)對(duì)稱2-彈性函數(shù)的構(gòu)造方法。

2 預(yù)備知識(shí)

n元布爾函數(shù)f0(x)=x1+x2+…+xn不僅是一個(gè)n?1階的彈性函數(shù)，還是一個(gè)旋轉(zhuǎn)對(duì)稱布爾函數(shù)，記f1(x)=1+x1+x2+…+xn=1+f0(x)，定義

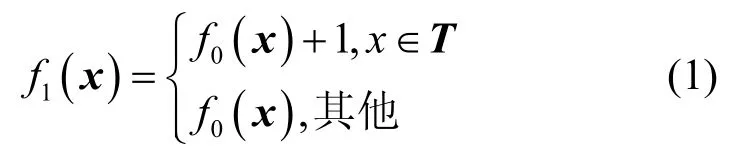
注意到，f1(x)為旋轉(zhuǎn)對(duì)稱函數(shù)的條件是當(dāng)且僅當(dāng)集合T是某個(gè)旋轉(zhuǎn)對(duì)稱函數(shù)的支撐集[21]，即為若干個(gè)旋轉(zhuǎn)對(duì)稱軌道的并集。向量x=(x1,x2,…,xn)∈的漢明重量為其分量中1 的個(gè)數(shù)，記為 wt(x)。

定義 1[15]設(shè)f(x)∈Bn，記1f={x∈|f(x)=1}，若有|1f|=2n?1，則稱f(x)是一個(gè)平衡函數(shù)，1f是布爾函數(shù)f(x)的支撐集或支撐矩陣，集合1f中的向量稱為f(x)的支撐向量，1+f(x)的支撐集或支撐矩陣簡(jiǎn)記為0f。

定義2[22-23]對(duì)于有限域F2上的w×n維矩陣A，如果線性空間中的每一個(gè)向量都在矩陣A的任意d列中出現(xiàn)相同的次數(shù)，則稱A是一個(gè)正交表 OA(w,n,2,d)。

定義3[23]如果V0和V1都是 OA(2n?1,n,2,d)，滿足V0∩V1=?，且V0∪V1=，則稱{V0,V1}為一個(gè)強(qiáng)度為d的正交表大集，記為 LOA(2n?1,n,2,d)。

文獻(xiàn)[23]給出了相關(guān)免疫函數(shù)和彈性函數(shù)與正交表和正交表大集間的關(guān)系，如果一個(gè)布爾函數(shù)f(x)的支撐矩陣1f是一個(gè)正交表OA(w,n,2,d)，則稱f(x)是一個(gè)d階相關(guān)免疫函數(shù)。如果f(x)既是平衡的，又是一個(gè)d階相關(guān)免疫函數(shù)，則f(x)是一個(gè)d-彈性函數(shù)，從定義3 可知，d-彈性函數(shù)的構(gòu)造等價(jià)于強(qiáng)度為d的正交表大集LOA(2n?1,n,2,d)的構(gòu)造，本文中的正交均指組合正交性。

下面，考慮循環(huán)群Cn=≤l≤n?1}在上的作用，變換定義為

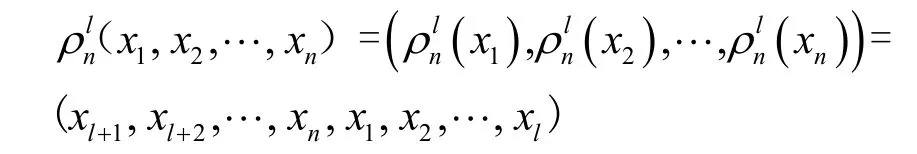
3 旋轉(zhuǎn)對(duì)稱軌道的性質(zhì)

為了研究旋轉(zhuǎn)對(duì)稱 2-彈性函數(shù)的構(gòu)造，下面將在文獻(xiàn)[15]的基礎(chǔ)上進(jìn)一步研究旋轉(zhuǎn)對(duì)稱軌道的性質(zhì)。假設(shè)變?cè)獋€(gè)數(shù)n=4t?1，其中t為正整數(shù)。

引理1[8]n元旋轉(zhuǎn)對(duì)稱長(zhǎng)軌道的總數(shù)為

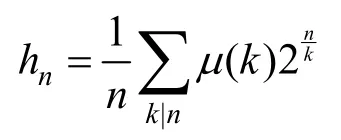
其中，μ(g)為墨比烏斯函數(shù)。

引理2[15]設(shè)f(x)為n元旋轉(zhuǎn)對(duì)稱布爾函數(shù)，1f=(c1,c2,…,cn)為f(x)的支撐矩陣，其中ci為1f的第i個(gè)列向量，那么存在一個(gè)置換矩陣P滿足ci+1=Pci,1≤i≤n?1。

引理3[15]設(shè)f(x)為n元旋轉(zhuǎn)對(duì)稱布爾函數(shù)，1f=(c1,c2,…,cn)為f(x)的支撐矩陣，ci為1f的第i個(gè)列向量，那么f(x)是2 階相關(guān)免疫函數(shù)的條件是當(dāng)且僅當(dāng)(c1,ck)是一個(gè)，其中，。

注：引理3 說明要判斷1f是否是強(qiáng)度為2 的正交表，只需判斷第1 列與第2～k列分別正交即可，這個(gè)結(jié)果大大簡(jiǎn)化了1f是否是強(qiáng)度為2 的正交表的判斷過程。

定理1設(shè)ROx是n維向量在循環(huán)群的作用下生成的一個(gè)旋轉(zhuǎn)對(duì)稱長(zhǎng)軌道，則矩陣ROx的任意2 列中，數(shù)對(duì)01 和10 出現(xiàn)的次數(shù)一定相等。

證明由引理2 可知，適當(dāng)排列ROx的行向量，則ROx可以表示為

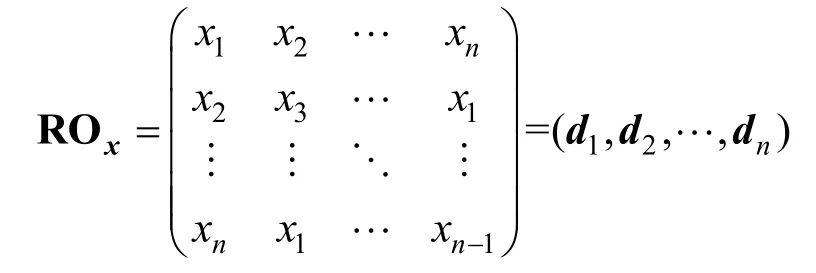
其中，di和dj分別是ROx的第i列和第j列，1≤i＜j≤n。下面，考慮di和dj這2 列中數(shù)對(duì)01和10 出現(xiàn)的次數(shù)。根據(jù)引理2，dj可以看作由di循環(huán)移位得到的，它們的分量中0 的個(gè)數(shù)和1 的個(gè)數(shù)分別相等，即如果列向量di的漢明重量wt(di)=w，則wt(dj)=w，其中，1≤i＜j≤n。不妨設(shè)由di和dj這2 個(gè)列向量構(gòu)成的n×2矩陣為

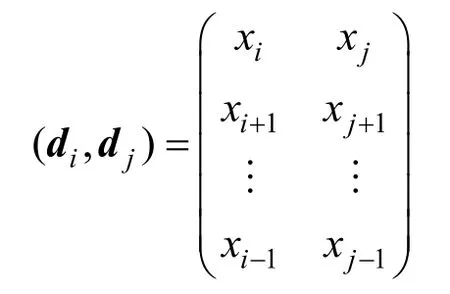
該矩陣行向量構(gòu)成的n個(gè)數(shù)對(duì)中00、01、10、11 出現(xiàn)的次數(shù)分別為N00、N01、N10、N11，則有式(2)所示的方程組成立。

由式(2)中第一個(gè)和第三個(gè)方程可知N01=N10，這就證明了矩陣ROx的任意2 列中，數(shù)對(duì)01 和10出現(xiàn)的次數(shù)一定相等。

注：①由式(2)可知，ROx的任意2 列中，數(shù)對(duì)11 和00 出現(xiàn)的次數(shù)之差為N11?N00=2w?n；②定理1 說明，一個(gè)軌道矩陣的任意2 列構(gòu)成的子矩陣的行向量中，數(shù)對(duì)00、01、10 和11 出現(xiàn)的次數(shù)實(shí)際上是由00、01 和11 這3 種數(shù)對(duì)確定的；③如果ROx是一個(gè)短軌道，且1 ＜|ROx|＜n，定理1的結(jié)論不一定成立。根據(jù)上面的性質(zhì)，為簡(jiǎn)化問題，本文給出如下定義。

定義4設(shè)n維向量在循環(huán)群的作用下生成的旋轉(zhuǎn)對(duì)稱的長(zhǎng)軌道為

在ROx的第1 列和第列中，數(shù)對(duì)00、01、11 出現(xiàn)的次數(shù)分別為bk?1,1、bk?1,2、bk?1,3，則稱如下的矩陣

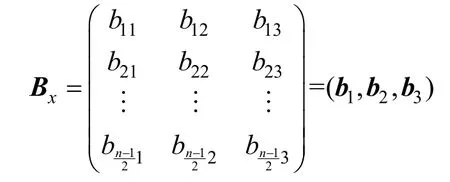
為旋轉(zhuǎn)對(duì)稱軌道ROx的數(shù)對(duì)分布矩陣。

特別地，若0r和1r分別表示r個(gè)連續(xù)的0和r個(gè)連續(xù)的1 構(gòu)成的行向量，則軌道{0n}和{1n}的數(shù)對(duì)分布矩陣為矩陣，即

對(duì)于n維向量x=(x1,x2,…,xn)，若，則容易證明在循環(huán)群Cn的作用下生成的旋轉(zhuǎn)對(duì)稱軌道的數(shù)對(duì)分布矩陣為

文獻(xiàn)[15]給出了旋轉(zhuǎn)對(duì)稱彈性函數(shù)的支撐矩陣的性質(zhì)，并給出了旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的等價(jià)刻畫，但是不能給出具體的構(gòu)造方法，為了構(gòu)造出具體的旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)，本文首先給出定理2。

定理2若t為正整數(shù)，當(dāng)n=4t?1時(shí)，則對(duì)任意的漢明重量為2t的向量，生成的軌道矩陣的數(shù)對(duì)分布矩陣為

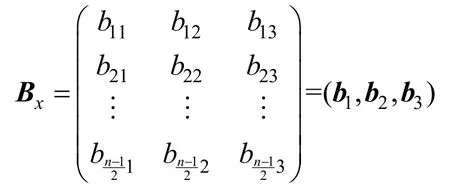
證明當(dāng)n=4t?1時(shí)，對(duì)任意的漢明重量為的向量x=(x1,x2,…,xn)，由于2t與4t?1互素，故該向量生成的旋轉(zhuǎn)對(duì)稱軌道一定是長(zhǎng)軌道。根據(jù)軌道矩陣對(duì)應(yīng)的數(shù)對(duì)分布矩陣的定義，在定理1 中，向量x=(x1,x2,…,xn)的漢明重量為w=2t，由式(2)可得，N11?N00=2w?n=1，這說明向量x=(x1,x2,…,xn)所在的軌道矩陣中由任意2 個(gè)列向量di和dj構(gòu)成的n×2維矩陣的行向量構(gòu)成的數(shù)對(duì)11 的個(gè)數(shù)N11總比數(shù)對(duì)00 的個(gè)數(shù)N00多1。令i=1，j跑遍集合{2,3,…,2t}，可得，即向量。證畢。

4 4t?1 元旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的一個(gè)新的等價(jià)刻畫

定理3對(duì)于式(1)所定義的函數(shù)f(x)，則f(x)是旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的充分必要條件是集合T滿足如下2 個(gè)條件。

1)T可以分解為集合S0和S1，使T=S0∪S1，其中

且|S0|=|S1|，其中，m和m'為非負(fù)整數(shù)，l1,l2,…,lm和s1,s2,…,sm'在集合{0,1,…,2t?1}中取值。

2)S0中不同的旋轉(zhuǎn)對(duì)稱軌道對(duì)應(yīng)的數(shù)對(duì)分布矩陣之和與S1中不同的旋轉(zhuǎn)對(duì)稱軌道對(duì)應(yīng)的數(shù)對(duì)分布矩陣之和相等。

證明必要性。如果f(x)是旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)，這意味著f(x)既是2-彈性函數(shù)，也是旋轉(zhuǎn)對(duì)稱函數(shù)。由于f(x)是2-彈性函數(shù)，根據(jù)彈性函數(shù)與正交表大集間的等價(jià)關(guān)系可知，{1f,0f}是上的一個(gè)強(qiáng)度為 2 的正交表大集，故1f和0f都是 OA(2n?1,n,2,2)。由于f(x)是旋轉(zhuǎn)對(duì)稱函數(shù)，1f和0f一定都是若干個(gè)旋轉(zhuǎn)對(duì)稱軌道的并集。另一方面，對(duì)1f中的旋轉(zhuǎn)對(duì)稱軌道進(jìn)行分類，將向量的漢明重量為偶數(shù)的所有旋轉(zhuǎn)對(duì)稱軌道記為S0，顯然S0可表示為一些旋轉(zhuǎn)對(duì)稱軌道的并集，即

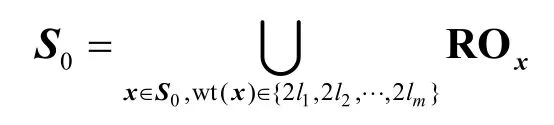
對(duì)0f中的旋轉(zhuǎn)對(duì)稱軌道進(jìn)行分類，將其中向量的漢明重量為奇數(shù)的旋轉(zhuǎn)對(duì)稱軌道記為S1，顯然S1也可表示為一些旋轉(zhuǎn)對(duì)稱軌道的并集，即

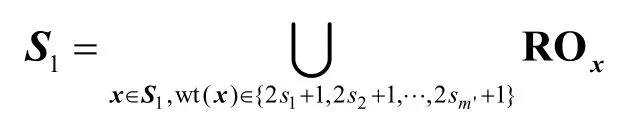
其中，m和m'為非負(fù)整數(shù)，l1,l2,…,lm和s1,s2,…,sm'在集合{0,1,…,2t?1}中取值，n=4t?1，故f(x)的支撐集可以表示為，由f(x)是平衡的，可知|S0|=|S1|，故條件1)成立。而由是一個(gè)OA(2n?1,n,2,n?1)可知，也是一個(gè)OA(2n?1,n,2,2)，這就意味著在的任意2 列中，數(shù)對(duì)00、01、10、11 出現(xiàn)的次數(shù)均為 2n?3，由于1f和都是OA(2n?1,n,2,2)，因而在1f的任意2 列中，以及在的任意2 列中，數(shù)對(duì)00、01、10、11 出現(xiàn)的次數(shù)均為 2n?3，注意到

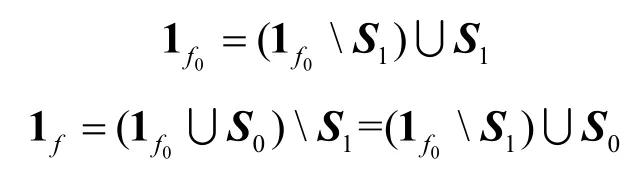
這說明S0中不同的旋轉(zhuǎn)對(duì)稱軌道對(duì)應(yīng)的數(shù)對(duì)分布矩陣之和與S1中不同的旋轉(zhuǎn)對(duì)稱軌道對(duì)應(yīng)的數(shù)對(duì)分布矩陣之和相等，即條件2)成立。必要性證畢。

充分性。由于f0(x)=x1+x2+…+xn是一個(gè)n元旋轉(zhuǎn)對(duì)稱彈性函數(shù)，故當(dāng)條件1)成立時(shí)，注意到T=S0∪S1，且S0和S1均為一些旋轉(zhuǎn)對(duì)稱軌道的并集，因而T可以看作一個(gè)旋轉(zhuǎn)對(duì)稱函數(shù)的支撐集，從而條件1)中定義的函數(shù)f(x)是一個(gè)旋轉(zhuǎn)對(duì)稱函數(shù)；再由f0(x)是彈性函數(shù)以及T=S0∪S1和|S0|=|S1|可知，f(x)是平衡函數(shù)；由正交表與彈性函數(shù)的關(guān)系，只需證明1f是強(qiáng)度為2 的正交表即可。

根據(jù)條件2)，由S0中不同的旋轉(zhuǎn)對(duì)稱軌道對(duì)應(yīng)的數(shù)對(duì)分布矩陣之和與S1中不同的旋轉(zhuǎn)對(duì)稱軌道對(duì)應(yīng)的數(shù)對(duì)分布矩陣之和相等可知，式(1)所定義的函數(shù)f(x)的支撐矩陣1f的 1 列分別與第列正交，再根據(jù)旋轉(zhuǎn)對(duì)稱函數(shù)的支撐矩陣的性質(zhì)以及引理3 可知，f(x)的支撐矩陣1f是一個(gè)OA(2n?1,n,2,2)。充分性證畢。

由定理3 可知，旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的構(gòu)造等價(jià)于尋找滿足定理3 條件的集合T，其中條件1) 是為了保證所構(gòu)造的函數(shù)是平衡的旋轉(zhuǎn)對(duì)稱函數(shù)，條件2) 是為了保證所構(gòu)造的函數(shù)是2-彈性的，利用定理1 和定理2 得到的結(jié)果，借助于定理3，可以構(gòu)造旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的無窮類，結(jié)合下面的例子，來說明本文方法的有效性。

5 一個(gè)構(gòu)造性的例子

以7 元旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的構(gòu)造為例，來說明本文的定理在一類4t? 1元旋轉(zhuǎn)對(duì)稱彈性函數(shù)的構(gòu)造中的應(yīng)用。由引理1 以及文獻(xiàn)[13]中的計(jì)算可知，若n=4t? 1為素?cái)?shù)，則循環(huán)群Cn在上的作用形成的軌道中，只有2 個(gè)短軌道{0n}和{1n}，其他的均為長(zhǎng)軌道。特別地，對(duì)于循環(huán)群作用在上，形成和這2 個(gè)短軌道，以及18 個(gè)長(zhǎng)軌道。為了方便，本文將旋轉(zhuǎn)對(duì)稱軌道及其對(duì)應(yīng)的數(shù)對(duì)分布矩陣分別表示為

行向量的漢明重量為3 和4 的軌道有如下10 個(gè)，其中，對(duì)應(yīng)的數(shù)對(duì)分布矩陣。

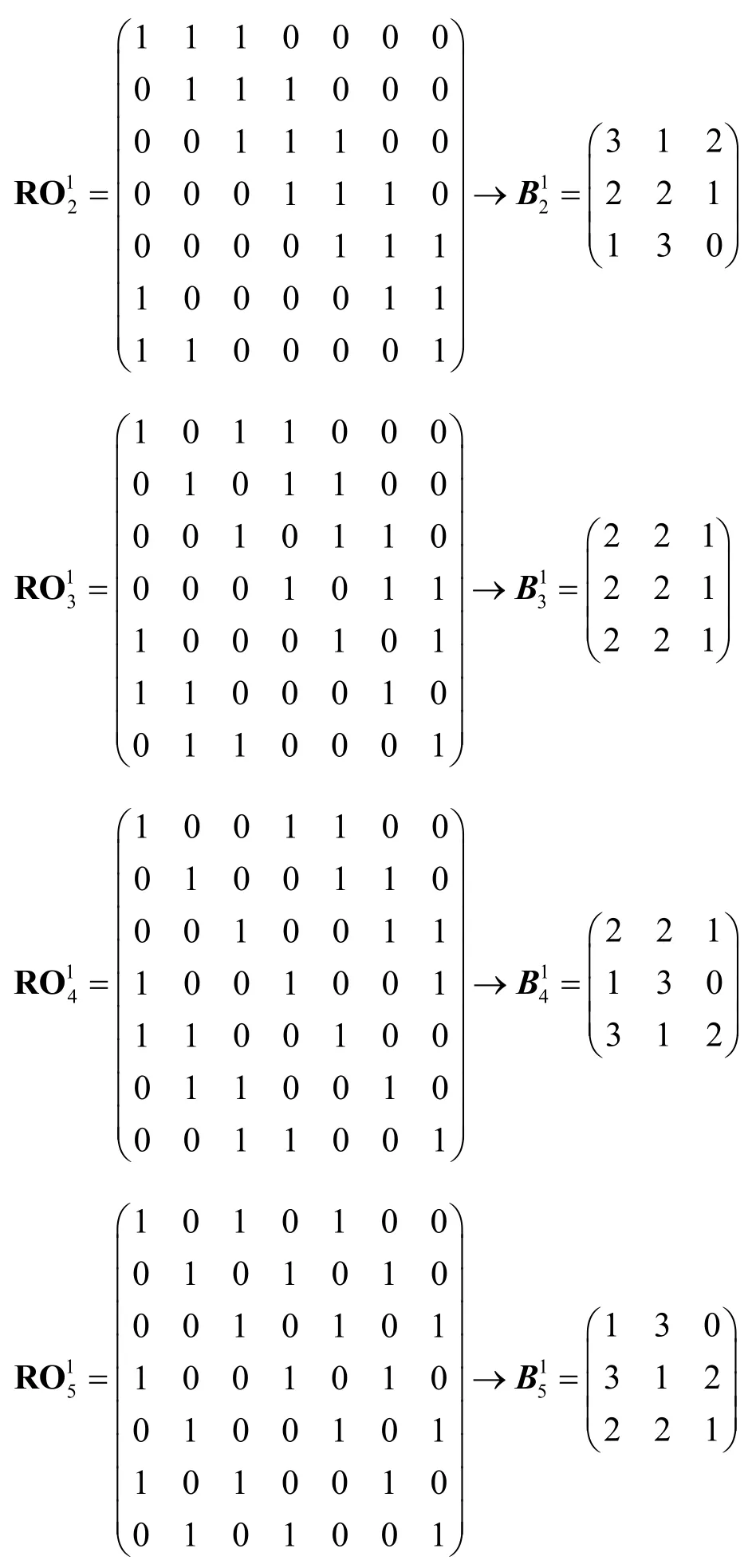
由定理3 可知，要構(gòu)造不同的7 元旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)，關(guān)鍵在于確定不同的S0和S1。若S0和S1中分別有2 個(gè)軌道，且其中之一是短軌道時(shí)，可以有如下的7 種方案。

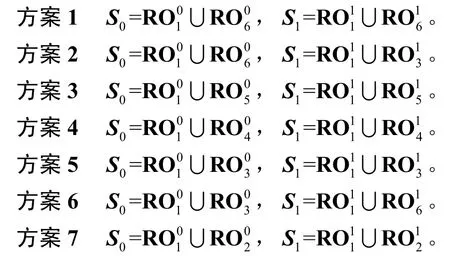
當(dāng)S0和S1按照上面的 7 種方案確定，取T=S0∪S1時(shí)，有|S0|=|S1|，對(duì)于式(1)定義的f(x)，根據(jù)定理3 可知，f(x)均為旋轉(zhuǎn)對(duì)稱2 階彈性函數(shù)。其中方案 1 確定的T=S0∪S1=，可以根據(jù)T中的向量計(jì)算所構(gòu)造函數(shù)的代數(shù)正規(guī)型。當(dāng)變?cè)獋€(gè)數(shù)n=4t?1較大時(shí)，如何根據(jù)所構(gòu)造函數(shù)的支撐矩陣得到其代數(shù)正規(guī)型，計(jì)算其非線性度是一個(gè)有待進(jìn)一步解決的問題。

6 結(jié)束語(yǔ)

旋轉(zhuǎn)對(duì)稱函數(shù)由于其特殊的結(jié)構(gòu)及其廣泛的應(yīng)用受到越來越廣泛的研究，關(guān)于旋轉(zhuǎn)對(duì)稱1-彈性函數(shù)的構(gòu)造與計(jì)數(shù)已經(jīng)有較多的結(jié)果，本文基于旋轉(zhuǎn)對(duì)稱軌道的數(shù)對(duì)分布矩陣的性質(zhì)，給出了一個(gè)旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的直接構(gòu)造方法，該方法能構(gòu)造出無窮多個(gè)旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)，但是由于所給出的函數(shù)都是以支撐集的形式給出的，因而不能給出所構(gòu)造函數(shù)的具體的代數(shù)正規(guī)型，或者說，需要煩瑣的計(jì)算轉(zhuǎn)換才能給出代數(shù)正規(guī)型，因而也就不能直接地給出其代數(shù)次數(shù)。其次，已有的一些文獻(xiàn)對(duì)所構(gòu)造的RSBF 是基于擇多函數(shù)得到的，因而對(duì)非線性度的估計(jì)計(jì)算有較多的數(shù)學(xué)工具可用，而本文構(gòu)造的函數(shù)是通過修改線性函數(shù)f0(x)=x1+x2+…+xn的支撐集而得到的，對(duì)其非線性度的計(jì)算也有較大的難度，這也是本文的一個(gè)不足。尋找有效地計(jì)算本文中所構(gòu)造的旋轉(zhuǎn)對(duì)稱2-彈性函數(shù)的代數(shù)表達(dá)式與非線性度將是下一步要解決的問題。