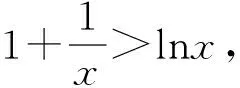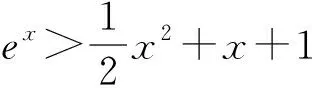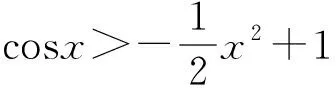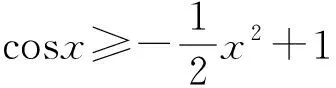提取結論 妙證不等式*
——談高中數學課堂教學中發展學生邏輯推理素養
福建廈門外國語學校石獅分校 (362700) 石明榮
“邏輯推理”是指從一些事實和命題出發,依據規則推出其他命題的素養.是得到數學結論、構建數學體系的重要方式,是數學嚴謹性的基本保證,是人們在數學活動中進行交流的基本思維品質.在高中數學課堂教學中,如何發展學生“邏輯推理”素養,關鍵在于如何引導學生發現問題和提出問題,然后利用所學知識進行表述和論證,形成有論據、有條理、合乎邏輯的思維品質和理性精神.筆者就如何在高中數學課堂教學環節,通過對幾個常見結論的證明和提取,進一步解決一類數學試題,發展學生的“邏輯推理”素養,拓展學生的解題思維能力,僅供同仁參考.
1 發現問題,提取結論,提升思維品質
例1 (人民教育出版社(A版)數學(選修2-2)第32頁,習題1.3B組第1題)利用函數的單調性,證明下列不等式,并通過函數圖象直觀驗證:
(1)sinx
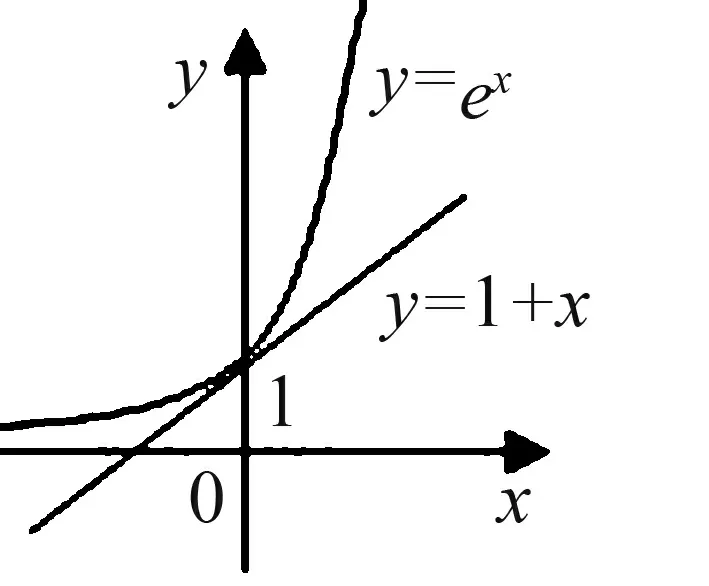
證明:(1)設f(x)=sinx-x,x∈(0,π),則f′(x)=cosx-1<0,所以f(x)在(0,π)上為減函數,從而f(x) 圖1 如圖1可知,當x∈(0,π)時,函數y=sinx的圖象在函數y=x的圖象的下方,從而當x∈(0,π)時,不等式sinx (2)設f(x)=ex-(1+x),則f′(x)=ex-1.當x<0時,ex<1,f′(x)<0,所以f(x)在(-∞,0)上為減函數.當x>0時,ex>1,f′(x)>0,所以f(x)在(0,+∞)上為增函數.從而f(x)≥f(0)=e0-1=0,當x≠0時,f(x)>0,不等式ex>1+x成立. 圖2 如圖2可知,當x≠0時,函數y=ex的圖象在函數y=1+x的圖象的上方,從而當x≠0時,不等式ex>1+x成立. 通過對以上兩道課本習題的證明,學生容易發現問題,進一步提取出如下結論: 結論1當x≥0時,sinx≤x; 結論2當x∈R時,ex≥1+x; 通過對以上兩道試題的證明,再次引導學生可以發現問題,容易提取到如下結論: 借助以上四個結論,可以快速解決部分與ex,lnx,sinx,cosx有關的不等式試題,達到事半功倍之效果,從而發展學生的“邏輯推理”素養,拓展解題思維能力. 例3證明下列不等式:(1)ex+cosx-3>lnx;(2)ex+cosx-1>xlnx. 例4任意x∈[0,+∞),不等式eax+cosx-sinx≥2恒成立.求實數a的取值范圍. 分析:不等式eax+cosx-sinx≥2中既有指數式,又有三角函數式,若能把三角函數化為多項式結構,結合上述結論,容易求得實數a的取值范圍. 綜上所述,教師通過引導學生挖掘“教材中的習題”,鼓勵學生大膽發現、猜測,進一步提取出一些結論,根據所提取的結論,大膽地去嘗試解題,從而發展了“邏輯推理”核心素養,拓展了邏輯推理能力.廣大教師應盡力構建以核心素養為導向的數學課堂,將核心素養的培養滲透到數學的每一個環節,實現“素養型”課堂的轉型.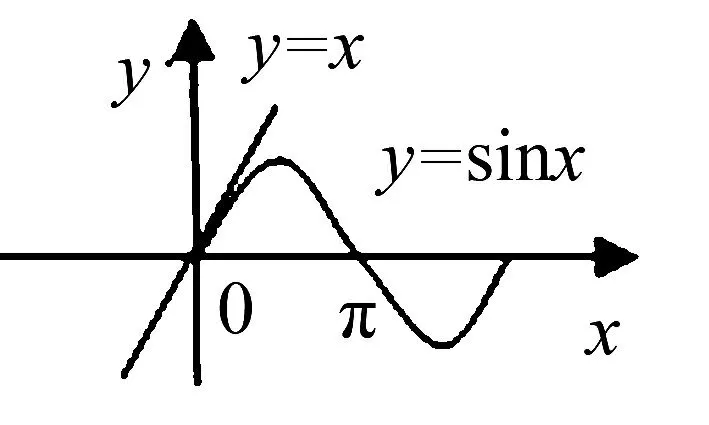
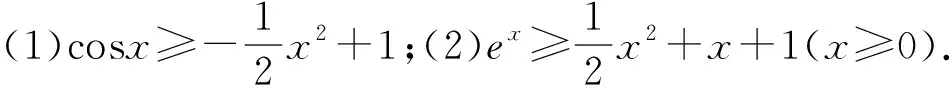
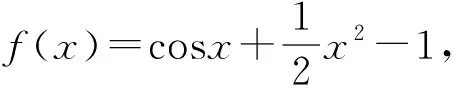
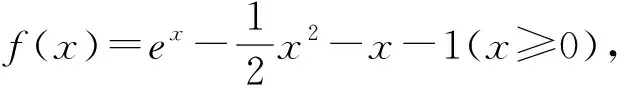
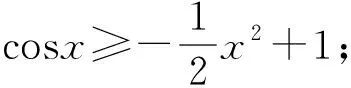
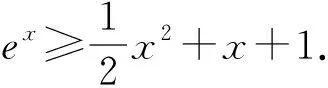
2 解決問題,發展學生“邏輯推理”素養,拓展學生解題思維能力