運用數形結合，提升直觀想象核心素養

江蘇省海門中學 (226100) 徐巧石

直觀想象是2017版的高中數學課程標準中提出了高中數學的六大核心素養之一，主要表現為：建立數與形的聯系，利用圖形描述問題，借助幾何直觀理解問題，運用空間想象認識事物.直觀想象并不是完全陌生的東西，與我們高中數學常用的數形結合思想有著密切的聯系以形助數或以數思形，通過建立數與形之間的雙軌通道，實現兩者的交流與聯系，是學生需要培養的一種素養.數學中有很多的結論常常是“看”出來的，會“看”就需要直觀想象素養.下面通過具體實例說明如何通過問題來體現直觀想象素養的水平與表現，探尋直觀想象素養培養的途徑.

一、養成作圖的習慣，積累“形”的常見表示

在教學中，面對具體數學問題，教師要引導學生主動利用圖形表達和分析問題，借助圖形的直觀將數學問題簡潔、形象化.想要靈活的借助圖形表述和解決問題，學生在平常的學習中需要做個有心人，積累“形”的一些常見表示，構建基本圖形庫.同時加強文字語言、符號語言和圖形語言的相互轉化.

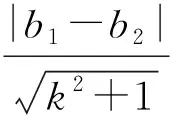
圖1

說明：本題考查的方向非常明確，即學生將“數”的語言轉化為“形”的表達，進而利用圖形解決問題.體現了直觀想象素養的水平一，即能夠通過圖形直觀認識數學問題，用圖形描述和表達熟悉的數學問題，啟迪解決問題的思路，體會數形結合.

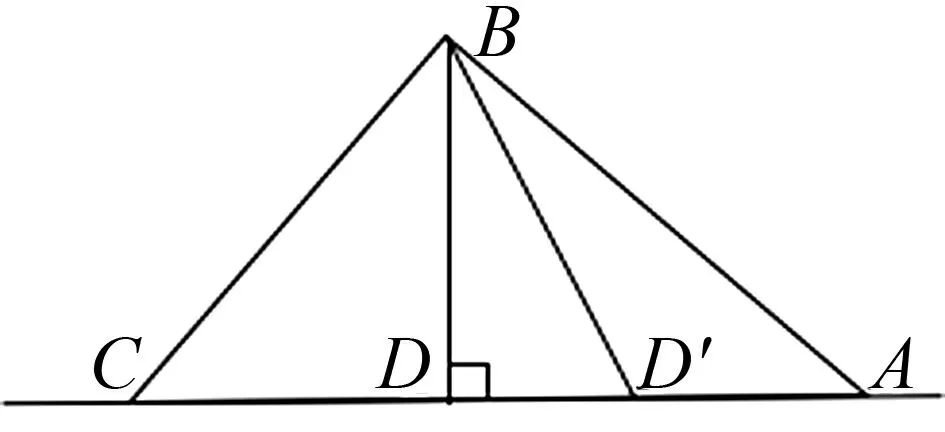
圖2

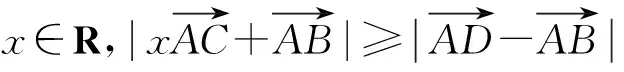
評注：此題的關鍵在于如何將題目中的條件等價轉化.畫圖可以發現題目就是求直線外一點到直線的最小值，所以在解題時要有圖形意識，積累圖形的等價表述語言，靈活的實現“數”與“形”之間的翻譯.體現了直觀想象核心素養水平一.

二、借助圖形的直觀表示，理解問題抓住本質

對于復雜的數學問題，運用“形”之直觀呈現問題的基本信息，借助“形”之直觀理解“數”之抽象，憑借“形”之直觀產生數量關系與問題本質屬性的感知，抓住問題本質，獲得解題思路.

例3 (2020蘇北四市一模·14)．設函數f(x)=|x3-ax-b|，x∈[-1,1]，其中a,b∈R.若f(x)≤M恒成立，則當M取得最小值時，a+b的值為.

圖3

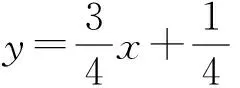
評注：本題是填空題的最后一題，有難度，直接從問題出發，問題可轉化為先求函數f(x)的最大值，再求關于最大值a,b的函數的最小值，分類討論繁多，運算量大.如果心中有圖形的意識，問題可以很快得到突破.此題體現了直觀想象素養的水平二，能夠在關聯的情境中，想象并構建相應的幾何圖形，借助圖形發現圖形與數量的關系，用圖形探索解決問題的思路，形成數學結合的思想，體會圖形直觀的作用和意義.

三、運用圖形認識數學問題，把握不同知識間的相互聯系

借助圖形，對具體數學問題進行觀察、分析、認知，從而對問題進行大膽的構造，巧妙的聯系，深入的思索.

圖4

評注：此題函數表達式復雜，要利用函數的相關性質對解析式進行化簡，由式子的結構聯想的直角三角形，進而構造問題的具體圖形，將函數的最值與三角形面積的最值建立起聯系，搭建起橋梁，運用圖形的直觀理解問題，從而快速的獲得解決問題的思路.

四、注重形與數之間的聯系，尋求解決問題的突破口

構建形與數之間的聯系，以數思形，以形助數，運用數形結合的思想方法，實現形與數之間的相互轉化，尋求解決問題的突破口，獲得解決問題的思路，發現問題的內在規律.

圖5

結語：上述案例中主要是以形助數，其實解題是從學生的角度出發的，從命題者的角度來看，在命制題目時的靈感有很多來自簡單圖形，借用了數加以表述.著名數學家華羅庚說：“數缺形時少直觀，形少數時難入微；數形結合百般好，隔離分家萬事休”.要提高學生的直觀想象素養，在教學中充分運用與滲透數形結合思想是可行的途徑.