巧用a2+b2≥2ab變式解題*

四川省自貢市衡川實驗學校 (643200) 李小強 鄧文俊 內江師范學院數學與信息科學學院 (641112) 劉成龍

a2+b2≥2ab形式優美、結構簡單，具有豐富的內涵，在高考和競賽中應用較為廣泛.當然，運用a2+b2≥2ab解決問題也具有一定的局限性，比如：a2+b2≥2ab解決一些分式不等式時就不能直接運用，需要將其適當變形后再使用.于是，很自然想到a2+b2≥2ab變形及應用這一重要的研究課題.本文探討a2+b2≥2ab幾種變形及變形的應用.

一、a2+b2≥2ab的幾個變式

變式是指相對于某種范式不斷變更問題情境或改變思維角度使事物的非本質屬性時隱時現，而事物的本質屬性保持不變的變化方式.陳景潤先生指出“題有千變，貴在有根．”這揭示了試題變式的內核.下面圍繞a2+b2≥2ab(當且僅當a=b時，等號成立)這一“根”展開豐富的變式研究.

變式2 若a,b∈R，則(a+b)2≥4ab.

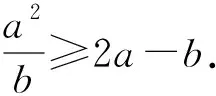
將變式3左右兩邊同時乘a可得：

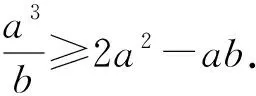
說明:(1)變式1—5取等條件均為a=b；

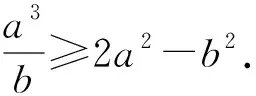
二、a2+b2≥2ab變式的應用

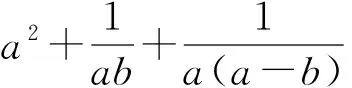
A.1 B.2 C.3 D.4

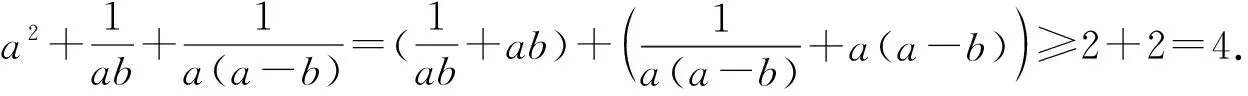
評注：例2、3解答中運用了變式2，解答的關鍵是分別運用變式2構建關于z,S的不等式.

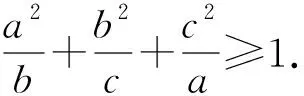
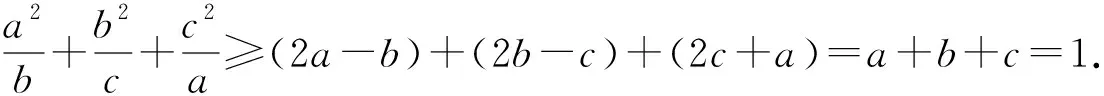
例5 (2009年江蘇卷21題)設a≥b>0，求證：3a3+2b3≥3a2b+2ab2.

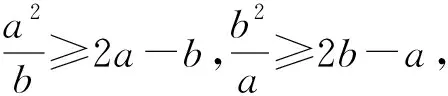
評注：例4、5證明過程中運用了變式3，極大簡化了問題證明過程，降低了學生的思維負荷.

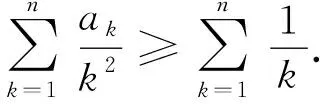
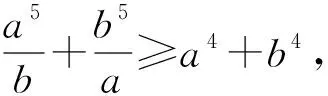
評注：本例中運用變式5有效地實現了降次，同時實現了分式不等式到整式不等式的轉化，大大降低了問題的難度.