基于動量加速零階減小方差的魯棒支持向量機
魯淑霞,蔡蓮香,張羅幻
(河北大學 數學與信息科學學院 河北省機器學習與計算智能重點實驗室,河北 保定 071002)
0 概述
間隔理論[1]由VAPNIK等人于1995年提出,其基于最小間隔最大化的原理,能夠從理論上有效地解釋其他許多學習方法的泛化性。在間隔理論的基礎上,文獻[2]提出了一種類似于boosting的算法Arc-gv,該算法同樣以最小間隔最大化的方式求解優化問題,但泛化性能較差。研究人員發現這種算法雖然充分利用了最小間隔的重要性,但是數據的間隔分布并不好。他們認為相比于最小間隔,數據的間隔分布可能對泛化性的影響更大,文獻[3]對其進行了理論證明。并且,文獻[4]還將該思想應用到傳統支持向量機(Support Vector Machine,SVM)分類中,獲得了更好的分類精度和泛化性能,充分說明相比傳統的最小間隔最大化的優化方法,對間隔分布進行優化更加重要。
在現實的分類問題中,由于人為或其他因素的影響,數據往往會存在一定的噪聲。如何對帶有噪聲的數據進行有效分類,是一個值得研究的問題。然而,傳統的SVM對噪聲數據不具有很好的魯棒性,這是因為傳統SVM使用無界的鉸鏈損失函數,對于噪聲數據會產生較大的損失值,使SVM的分類超平面嚴重偏離最優超平面,影響最終的分類效果。于是,許多研究從改進損失函數角度出發,提高SVM對噪聲數據的魯棒性。文獻[5]在鉸鏈損失的基礎上提出了一種截斷的鉸鏈損失,通過引入一個小于0的截斷參數s,使鉸鏈損失有一個確定的界限,解決了噪聲數據帶來較大損失的問題。通過最大化2個類之間的最小分位數距離,文獻[6]提出了彈球損失,彈球損失是最大化2個類之間的分位數間距,而不是最小間距,由此提高了對屬性噪聲的識別性,改善了分類性能。文獻[6]在此基礎上提出了一種截斷的彈球損失(truncated pinball loss)。相比于最初的pinball損失,文獻[7]提出的損失函數增加了兩段水平部分,使得損失函數的值有一個固定的上界,降低了噪聲數據對算法性能的影響。
求解建立的SVM模型也是一個值得研究的問題。隨機梯度下降(Stochastic Gradient Descent,SGD)算法是一階優化方法,廣泛應用于各種優化問題中,并衍生出許多優秀的算法,如文獻[8]提出的Pegasos算法,該算法在每次迭代中隨機選擇一個樣本計算梯度,并以此代替全梯度。由于通常假設樣本是獨立同分布的,從而隨機抽取單個樣本的目標函數的梯度是整個目標函數梯度的無偏估計,進而可用每次迭代僅處理單個或部分樣本的隨機優化方法來代替批處理方法,但是該方法存在方差,隨著迭代次數的增加,方差也逐漸累加,收斂速率不可避免地受到影響。為降低方差的影響,文獻[9]提出了減小方差的隨機梯度(Stochastic Variance Reduction Gradient,SVRG)下降算法。該算法分為內外兩層循環,僅在外層循環計算全梯度,降低了計算量。在內層循環中引入梯度修正項,降低了方差對算法的影響,提高了算法的性能。文獻[10]在SVRG算法的基礎上依據Nesterov的動量加速技巧,提出了快速減小方差的隨機梯度(Fast Stochastic Variance Reduced Gradient,FSVRG)下降[11]算法。FSVRG是SVRG的一個加速變種,在每次內層迭代中引入了動量加速技巧,不僅計算在當前迭代中的梯度值,同時考慮了上一輪的梯度變化,與SVRG相比提高了算法的收斂速度。此外,在文獻[12]提出的結構凸優化問題和文獻[13]提出的經典的Katyusha算法以及文獻[14]提出的加速隨機鏡像下降算法中均引入了動量加速技巧,且都獲得了較好的性能。
上述所提方法雖然可以有效地降低方差對算法的影響,但是在每次迭代中均需要計算梯度,求解梯度困難或者不能求解梯度的模型,會增加額外的開銷。因此,文獻[15]把零階優化方法和減小方差策略相結合,提出一種零階減小方差的隨機梯度(Zeroth Order-Stochastic Variance Reduced Gradient,ZO-SVRG)下降方法。ZO-SVRG不需要計算梯度的準確數值,而是用函數值逼近梯度,有效地解決了復雜模型不能計算梯度的問題,具有較高的實用性。文獻[16]基于零階優化的思想,結合交替方向乘子法,提出一種在線的零階交替方向乘子算法(ZOO-ADMM)。該算法既避免了梯度的計算,又利用了交替乘子法能夠處理復雜結構的優勢,經過理論分析和實驗驗證說明了所提方法的有效性。
為解決傳統SVM對噪聲敏感的問題,本文通過引入間隔分布和新形式的損失函數,提出一種基于動量加速零階減小方差的魯棒支持向量機(MA-ZOVR)。
1 相關工作

(1)
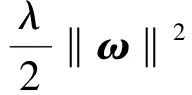
1.1 零階減小方差算法

(2)
其中,G(ωt)稱為梯度修正項。
零階梯度估計用函數值近似代替,坐標梯度估計如下[15]:
(3)
其中,el表示一個標準基向量,在第l個坐標處為1,其他坐標處為0,μl>0表示光滑參數。
ZO-SVRG算法如下:
算法1ZO-SVRG算法
輸入外層迭代輪數S,內層迭代次數T,學習率η,光滑參數μ

1.for s=1,2,…,S
5. for t=0,1,…,T-1
6. 隨機抽取一個樣本i,進行梯度更新

8. end
10.end
1.2 動量加速技巧
文獻[17]指出Nesterov[10]的動量加速技巧可以加速隨機減小方差算法的收斂,能夠使強凸問題和一般凸問題的收斂速度達到較高的水平。隨機減小方差算法均分為內外雙重循環,引入動量加速技巧后,每次內層迭代的梯度由式(4)、式(5)2個更新規則構成:
(4)
(5)
根據式(4)計算當前迭代中的梯度變化情況,其中,vt+1為輔助變量,ηs為更新步長。
式(5)表示,結合上一輪梯度的結果,得出本次內層迭代最終的梯度更新規則。其中,ρs表示動量權重系數。
引入動量加速技巧后的梯度更新規則并不僅僅依賴于當前迭代的梯度變化情況,并且考慮了上一輪的最終結果。所以,計算當前迭代中的梯度時,都會有一個之前梯度的作用。如果這次的梯度和上一輪的梯度方向相同,則會因為之前的速度繼續加速;如果這次的梯度和上一輪的梯度方向相反,則不增加或減少過多。因此,引入動量加速技巧后,會使梯度在每次的下降過程中減少擺動的幅度,加速算法的收斂。
2 動量加速零階減小方差的魯棒SVM
基于文獻[4]的理論證明,在本文中用間隔分布均值代替傳統的最小間隔,充分考慮每個樣本的分布情況。間隔分布均值為:
(6)
此外,傳統SVM的損失函數為鉸鏈損失。但由于鉸鏈函數無界性的特點,對于噪聲數據會帶來較大的損失,使分類性能下降。因此,為了降低噪聲數據的影響,結合指數函數的結構特點,引入一種新形式的損失函數:
(7)
損失函數曲線如圖1所示。

圖1 損失函數曲線示意圖Fig.1 Schematic diagram of loss function curve
在圖1中,橫坐標表示間隔,即yiωTxi,一般又將其稱為函數間隔。在SVM的分類任務中,可以通過函數間隔的正負來判定或表示樣本分類的正確性;縱坐標表示對應的損失函數值。下文對損失函數進行具體的分析:
1)當1-yiωTxi=0時,yiωTxi=1>0,樣本正確分類,對應的損失值為0。
2)當1-yiωTxi<0時,yiωTxi>1>0,樣本正確分類,對應的損失值為0。
3)當1-yiωTxi>0時,yiωTxi<1,這時存在2種情況:
(1)當0 (2)當yiωTxi<0時,樣本錯誤分類。 在3)中的2種情況表示的是噪聲數據的分類狀態。可以明顯地看出噪聲數據的損失值限制在了[0,1]之間,避免了出現噪聲數據帶來過大損失的情況,從而降低了噪聲數據對分類性能的影響。 通過引入間隔分布均值以及新的損失函數,在線性輸入空間建立新的優化模型如下: (8) 對于優化模型的求解,基于零階優化減小方差的思想,配合動量加速技巧,提出一種基于動量加速零階減小方差(MA-ZOVR)算法。 在線性MA-ZOVR算法中,首先對梯度進行估計,改變傳統的梯度計算方式,通過式(3)坐標梯度估計法,計算出函數值并近似代替梯度。為降低方差對算法性能的影響,引入了式(2)的梯度修正項。最后結合動量加速技巧,在內層迭代中使用式(4)和式(5)進行梯度的更新。 線性MA-ZOVR算法如算法2所示。 算法2線性MA-ZOVR算法 輸入外層迭代輪數S,內層迭代次數T,光滑參數μ,正則化參數λ 1.for s=1,2,…,S 6. for t=0,1,…,T-1 7. 隨機抽取一個樣本i進行梯度更新 10. end for 12. v0=vT 13.end for 在非線性輸入空間,定義如下的優化問題: (9) 一般地,在非線性特征空間,優化問題中φ(xi)的維數很高,求解非常復雜。本文通過表示定理[8,20]對式(9)進行變形: (10) 其中,α=[α1,α2,…,αn]T,X=[φ(x1),φ(x2),…,φ(xn)]。根據式(10)可得: yiωTφ(xi)=yi(Xα)Tφ(xi)= yiαTXTφ(xi)=yiαTGi 其中,G=XTX表示核矩陣,Gi表示G的第i列,式(8)可以表示為: (11) 對于變形后的優化問題式(11),不再將其轉換成對偶形式,而是使用提出的非線性MA-ZOVR算法直接求解。非線性MA-ZOVR算法和2.1節提到的線性算法有著相同的框架,不同是非線性MA-ZOVR算法優化變量為α引入了核運算。 非線性MA-ZOVR算法如算法3所示。 算法3非線性MA-ZOVR算法 輸入外層迭代輪數S,內層迭代次數T,光滑參數μ,正則化參數λ 1.for s=1,2,…,S 6. for t=0,1,…,T-1 7. 隨機抽取一個樣本i,進行梯度更新 10. end for 12. v0=vT 13.end for 在給出MA-ZOVR算法的收斂性結論前,對MA-ZOVR算法用到的相關知識進行總結如下: 1)整體框架:使用零階減小方差優化框架,降低了方差的影響,同時避免了重復的梯度計算。 2)梯度計算方法:使用坐標梯度估計[12,15]。雖然多了O(d)次的函數查詢(計算函數值),但是可以獲得更精確的梯度估計。 3)梯度更新方法:在減小方差的基礎上結合動量加速技巧[18,21-22],加速算法的收斂。 本節驗證本文提出的動量加速零階減小方差的魯棒SVM(MA-ZOVR)算法的性能,主要從以下5個方面進行實驗: 1)抗噪性實驗:進行線性MA-ZOVR算法和非線性MA-ZOVR算法的抗噪性實驗。 2)模塊化實驗:分別驗證新的求解方法和新的優化模型的有效性。 3)方差分析實驗:針對非線性情況,對比本文提出的算法和標準隨機梯度下降算法(SGD),驗證算法減小方差策略的有效性。 4)收斂速度分析實驗:針對非線性情況,對比本文的動量加速零階減小方差算法和原始的零階減小方差(ZO-SVRG)算法,驗證算法收斂速度的加速。 5)參數分析實驗:分析實驗中的主要參數對算法精度的影響。 實驗程序運行環境為Matlab R2016a。實驗數據來源于KEEL網站(訓練集和測試集的比例均為4∶1),主要分為2個部分:第1部分為常規噪聲數據集,依次選取含有0%、5%、10%和15%屬性噪聲的數據進行實驗;第2部分為相對較大規模的標準數據集,為了驗證算法的抗噪性,依次對這幾個數據集加入0%、5%、10%和15%均值為0及方差為0.5的高斯噪聲。實驗數據集如表1所示。 表1 實驗數據集Table 1 Experimental datasets 本節進行線性MA-ZOVR算法和非線性MA-ZOVR算法的抗噪性實驗。為了使實驗效果更加明顯,下面給出本文提出的MA-ZOVR算法和傳統的SVM算法(文獻[8]中的Pegasos算法求解優化問題1以及原始零階減小方差算法,文獻[15]中的ZO-SVRG算法求解優化問題1)的測試分類結果。下文所給結果均為五折交叉實驗的平均值。線性算法的比較結果如表2所示。 表2 不同線性算法分類準確率比較Table 2 Comparison of classification accuracy of different linear algorithms % 從表2可以看出,在給定的9組不同噪聲比的數據集中,本文提出的線性MA-ZOVR算法與線性Pegasos算法以及線性ZO-SVRG算法相比,均具有較高的準確率,這說明了本文提出的算法有效地提高了SVM的抗噪性,具有較高的分類精度。另外,從給出的結果還可以看出,隨著數據噪聲百分比的增大,分類準確率隨之降低。 由于非線性MA-ZOVR算法涉及到了核矩陣的運算,因此在處理較大規模數據時,運行時間過長。為了提高實驗效率,在常規數據集上進行非線性MA-ZOVR算法的抗噪性對比實驗。非線性MA-ZOVR算法、非線性Pegasos算法以及非線性ZO-SVRG算法的實驗結果如表3所示,其中均使用高斯核函數。 表3 不同非線性算法分類準確率比較Table 3 Comparison of classification accuracy of different nonlinear algorithms % 從表3可以看出,在給定的不同噪聲比的6組數據集中,本文提出的非線性MA-ZOVR算法與非線性Pegasos算法以及非線性ZO-SVRG算法相比,均具有較高的準確率,這說明非線性MA-ZOVR算法的抗噪性能好,能夠改善傳統SVM的不足,降低了噪聲數據對分類效果的影響。 本文提出的MA-ZOVR算法包括對優化模型和求解方法2個方面的改進。為更好地說明問題,下文進行模塊化實驗。模塊化實驗1:對改進后的優化模型式(7)、式(10)分別使用傳統的隨機梯度下降的求解方法,記為MA+SGD;模塊化實驗2:對傳統的SVM模型式(1)使用提出的MA-ZOVR優化求解方法(包括線性和非線性),記為SVM+MA。線性算法模塊化實驗結果如表4所示。 表4 不同線性算法模塊化實驗結果比較Table 4 Comparison of modularization experimental results of different linear algorithms % 從表4可以看出,在給定的不同噪聲比的9組數據集中,本文提出的線性MA-ZOVR算法的精度優于實驗1的精度,這說明了在線性情況下本文提出的求解方法的有效性。同樣,根據與實驗2結果的對比也可以看出,在線性情況下本文提出的優化模型的有效性。非線性MA-ZOVR算法的模塊化實驗結果如表5所示。從表5可以看出,在給定的不同噪聲比的6組數據集中,本文提出的非線性MA-ZOVR算法分類精度均高于實驗1和實驗2。按照上述的分析方法,分別驗證了在非線性情況下本文提出的求解方法和優化模型的有效性。 表5 不同非線性算法模塊化實驗結果比較Table 5 Comparison of modularization experimental results of different nonlinear algorithms % 本節進行非線性MA-ZOVR算法和傳統隨機梯度下降(Stochastic Gradient Descent,SGD)算法的方差分析實驗。圖2和圖3為MA-ZOVR算法和傳統SGD算法對不同噪聲比的wdbc數據集進行分類的方差對比。 圖2 不同噪聲比(0%,5%)的方差對比結果Fig.2 Variance comparison results of different noise ratios(0%,5%) 圖3 不同噪聲比(10%,15%)的方差對比結果Fig.3 Variance comparison results of different noise ratios(10%,15%) 從圖2和圖3可以看出,在迭代過程中對于不同噪聲比的實驗數據,隨機梯度下降算法的方差一直維持一個比較大的值,下降幅度較小。對比結果可以看出,本文提出的MA-ZOVR算法的方差較小,且隨著迭代的進行逐步降低,最后減小到一個接近于零的定值,表明本文算法可以有效地對方差進行修正。 本節進行非線性MA-ZOVR算法和非線性ZO-SVRG算法的收斂速度對比實驗。圖4和圖5為2種方法對不同噪聲比的ionosphere數據進行分類的收斂速度對比。 圖4 不同噪聲比(0%,5%)的目標函數值Fig.4 Objective function values of different noise ratios(0%,5%) 圖5 不同噪聲比(10%,15%)的目標函數值Fig.5 Objective function values of different noise ratios(10%,15%) 從圖4和圖5可以看出,對于不同百分比的噪聲數據,使用本文提出的MA-ZOVR算法進行求解時,前200次迭代過程中函數值逐步減小,在200次以后函數值逐漸趨近于一個定值;對比結果可以看出,原始的ZO-SVRG算法在前400次迭代中函數值一直處于減小狀態,直到400次之后函數值才逐漸趨于穩定,表明本文算法通過引入動量加速技巧,有效地提高了算法的收斂速度。 本節進行線性MA-ZOVR算法和非線性MA-ZOVR算法的參數分析實驗。對于線性MA-ZOVR算法主要分析正則化參數λ對分類精度的影響;對于非線性MA-ZOVR算法分析正則化參數λ和高斯核函數的寬度sigma兩者共同對分類精度的影響。表6、表7給出不同噪聲比的ionosphere數據分類的準確率。 表6 線性MA-ZOVR算法分類準確率Table 6 Classification accuracy of linearMA-ZOVR algorithm % 表7 非線性MA-ZOVR算法分類準確率Table 7 Classification accuracy of nonlinearalgorithm MA-ZOVR 對表6進行橫向對比,在固定數據噪聲比的條件下,根據分類精度可以看出,當參數λ=0.001時的分類效果較好。 首先對表7進行橫向對比,在固定噪聲比和sigma的條件下,根據分類精度可以看出,對于給定的不同λ值,分類效果差異不大,當λ=0.001時分類效果稍好于其他的取值;其次對表7進行縱向對比,在固定噪聲比和λ=0.001的條件下,根據結果可得,當sigma=1時分類效果較好。因此,當參數sigma=1,λ=0.001時分類性能最優。 為提高SVM的抗噪性,本文提出一種基于動量加速零階減小方差的魯棒SVM算法。通過引入間隔均值項和指數形式的損失函數建立新的優化模型,并在零階減小方差的基礎上引入動量加速技術求解優化模型。實驗結果表明,該方法能夠有效提高SVM的抗噪性,降低在迭代中累積的方差,同時加快算法的收斂速度。下一步將在本文研究的基礎上,結合L1正則化項,設計新的算法對帶有噪聲數據分類問題的稀疏化進行研究。2.1 線性MA-ZOVR算法
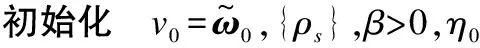



2.2 非線性MA-ZOVR算法



2.3 MA-ZOVR算法的收斂性分析
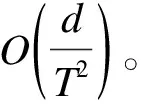
3 實驗結果與分析

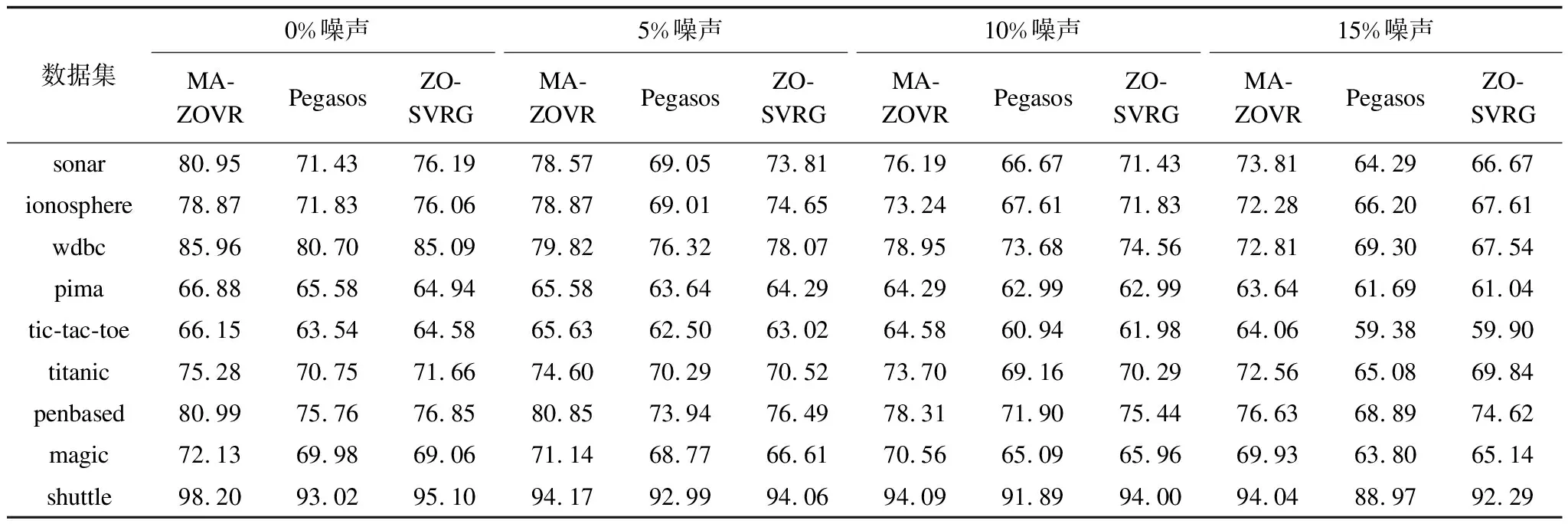
3.1 抗噪性實驗
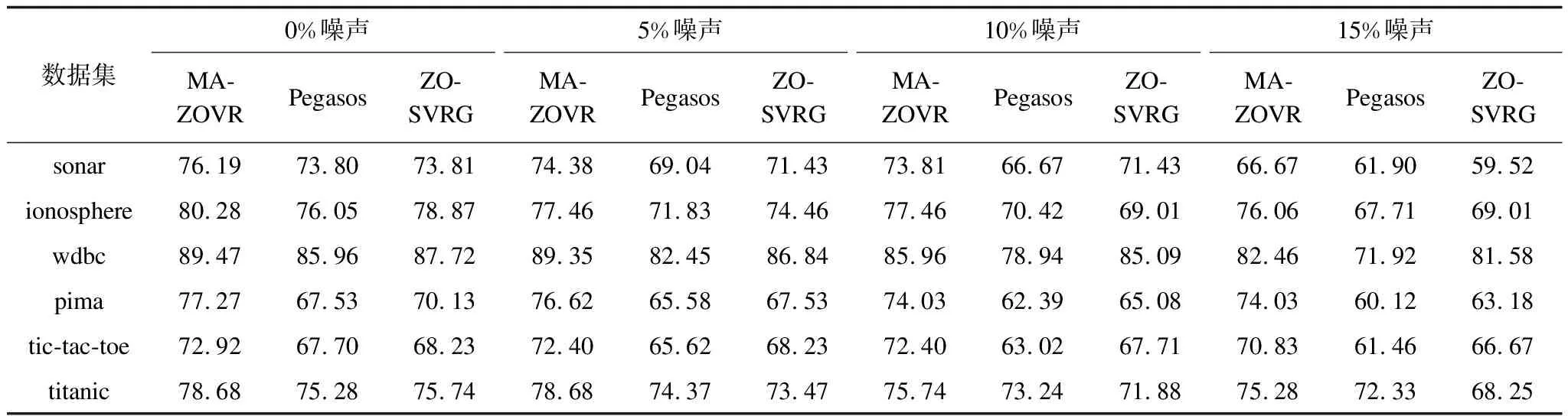
3.2 模塊化實驗


3.3 方差分析實驗


3.4 收斂速度分析實驗


3.5 參數分析實驗
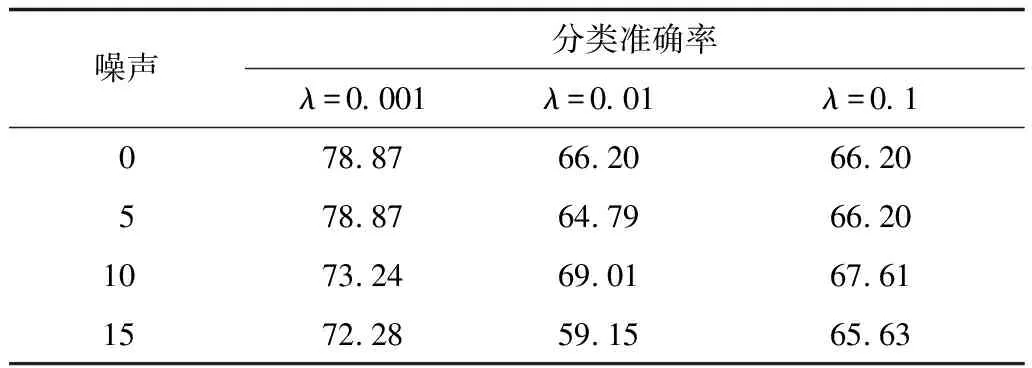

4 結束語

