多運動模式下的累積誤差修正行人航位推算算法

施元昊,張健銘,徐正蓺,滕國偉

(1.上海大學 通信與信息工程學院,上海 200444; 2.中國科學院上海高等研究院,上海 201210; 3.中國科學院大學 電子電器與通信工程學院,北京 100049)

0 概述

近年來,隨著智能移動設備的普及和物聯網的快速發(fā)展,人們對室內商場定位、安全應急定位以及無人快遞配送定位等室內定位需求不斷增長,采用慣性測量單元(Inertial Measurement Unit,IMU)的行人航位推算(Pedestrian Dead Reckoning,PDR)算法[1-3](以下稱為慣性導航定位算法)由于其無需預先布設基礎設施且受外界干擾較小,因此被廣泛應用。

由于PDR算法為自主式定位存在累計誤差,因此通常采用零速校正(Zero Velocity Update,ZUPT)或零角速度校正(Zero Angle Rate Update,ZARU)的方式對累積誤差進行校正,該方式通過設定固定閾值確認腳部是否處于觸地階段從而判斷行人腳步是否處于零速區(qū)間。如果行人腳步處于零速區(qū)間,則對慣性導航定位算法進行零速校正。慣性導航定位算法對于單一運動模式具有較好的誤差抑制效果,但是對于慢走、中速走和快走等多種運動模式,其零速檢測的固定閾值各不相同,閾值過大會造成判定的零速區(qū)間較大,對非零速點進行零速校正后導致定位精度降低。與此類似,閾值過小也會導致定位精度降低。因此,對于勻速的單一運動模式可通過固定閾值方式進行零速校正,而對于多種運動模式并存的混合運動模式,需對閾值進行動態(tài)調整以適應各種運動模式。此外,盡管零速校正算法在一定程度上可減少累積誤差,但因為該算法模型與真實人體運動模型存在差異,所以仍會出現殘余累積誤差。因此,慣性導航定位算法通常需要輔助定位,研究人員提出超寬帶[4]、無線指紋定位[5]、藍牙定位[6]和ZigBee定位[7]等技術來輔助實現室內定位,并幫助IMU消除累積誤差。在目前的應用場景下,采用輔助定位的PDR算法主要在坐標點修正誤差[8]或利用建筑物已有信息修正誤差。但這些修正誤差的方式對底層數據校正不足,部分定位方式需預先對基礎設施進行建模和繪圖。

針對多運動模式下零速校正效果較弱的問題,本文提出一種采用長短時記憶(Long Short-Term Memory,LSTM)模型的零速校正算法。構建LSTM網絡學習不同運動模式下的運動與時序特征,以實現對零速校正的自適應判定。在此基礎上,采用多傳感器數據融合的方式修正慣性傳感器數據以減少殘存累積誤差,同時優(yōu)化差分進化(Differential Evolution,DE)算法的目標函數防止出現過擬合現象。

1 基于多運動模式的自適應零速校正算法

在目前對零速校正算法的研究中,主要關注單一運動模式,對多運動模式研究較少。由于在多運動模式下采用固定閾值修正累積誤差的零速校正算法修正效果會減弱,無法自適應地應對不同運動模式,因此在實際場景下需采用一種新的零速檢測算法來應對多運動模式。

1.1 零速校正算法

零速校正算法是一種能有效減少由累積誤差與算法誤差所引起定位誤差的算法,該算法首次由FELIZ提出,并由JIMENEZ等人加以完善而形成[9]。在此基礎上,文獻[10]提出一種融合卡爾曼濾波算法的零速校正算法。零速校正算法主要包括零速檢測和誤差校正兩部分。

行人在運動狀態(tài)中,其腳步運動數據呈現周期性變化,該周期稱為步態(tài)周期。一個完整的步態(tài)周期包括觸地、起步、懸空和落腳4個階段[11],其中觸地階段是零速校正的主要階段,在該階段行人腳步位置與速度保持不變[12],陀螺儀測得的角速度和加速度計測得的加速度變化理論上為0,因此,可通過該特征判定是否為零速狀態(tài)[13]。

當零速檢測算法檢測到行人腳步處于零速狀態(tài)時,則開始進行誤差校正。最簡單的誤差校正方式為:假如判定行人處于零速狀態(tài),則將慣性傳感器測得的角速度和加速度都校正為零。在實際應用中,通常采用基于卡爾曼濾波的誤差抑制算法[14]對零速狀態(tài)下行人的位姿信息進行誤差修正,在非零速狀態(tài)下只更新狀態(tài)誤差協方差矩陣[15]。

上述零速校正方式可在一定程度上減少累積誤差帶來的影響,特別是中速步行時具有較好的效果。然而因為零速檢測采用固定閾值的方式判定零速狀態(tài),在多種運動模式下零速檢測會因誤判而對運動點采取零速校正,從而導致定位精度下降,所以在不同運動模式下零速檢測的閾值會發(fā)生變化,所設定的閾值隨行走速度的加快而增大。因此,在不同的運動模式下,閾值應動態(tài)調整以保持定位的準確性。

圖1為快速行走閾值調整前后零速檢測點的變化情況。可以看出,當運動模式為快速行走時,若采用中速行走時的零速判定閾值,則會導致零速校正區(qū)間明顯減小。圖2為閾值調整前后行人軌跡。

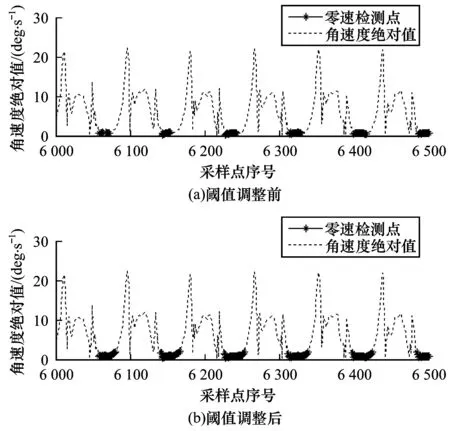
圖1 快速行走閾值調整前后零速檢測點變化Fig.1 Change of zero speed detection point beforeand after the threshold adjustment of rapid walking

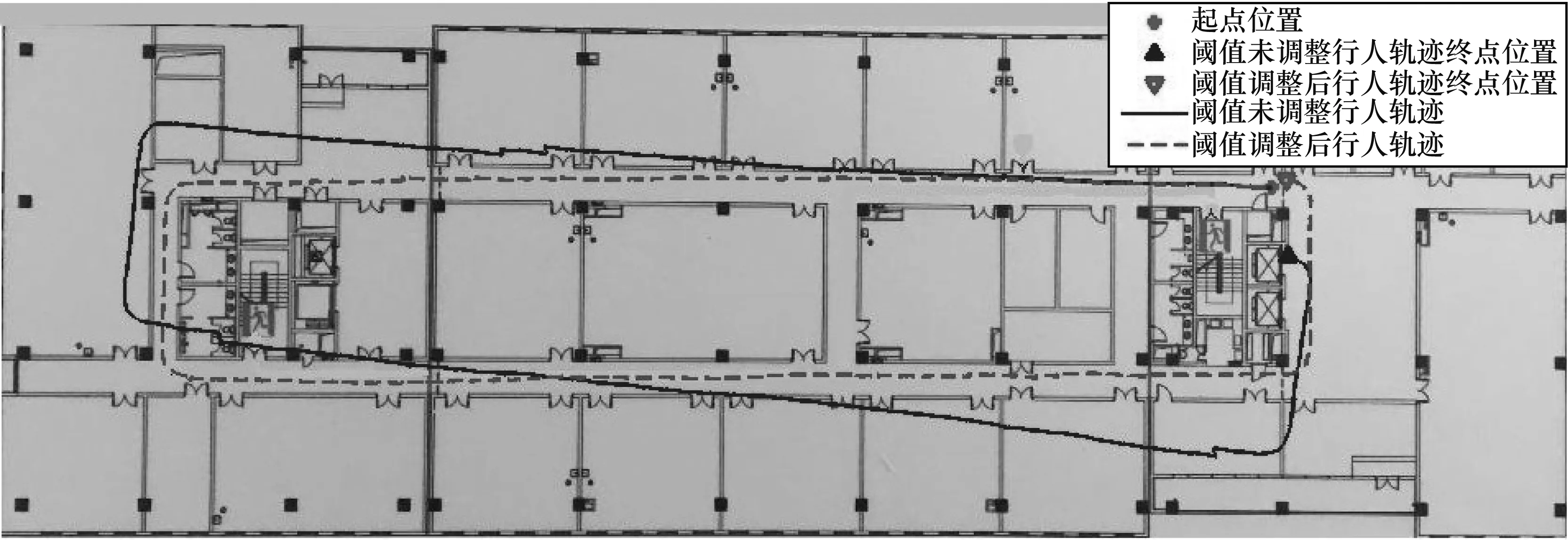
圖2 閾值調整前后行人軌跡Fig.2 Pedestrian trajectory before and after the threshold adjustment

結合圖1和圖2可知,零速檢測區(qū)間的減小造成零速校正效果減弱,從而降低定位精度。若在快速行走模式下仍采用中速行走模式的閾值,則行人最終的定位誤差達到3 m(見圖2中實線框),而當閾值提高后,行人軌跡定位誤差減小到0.4 m(見圖2中虛線框)。因此,對于不同運動模式,閾值需進行相應調整。因為不同運動模式下運動具有相應特征,所以可采用深度學習的方式根據不同運動特征進行零速區(qū)間判定。考慮到行人在相同運動狀態(tài)下步態(tài)周期一般不改變,即可認為行人在相同運動狀態(tài)下任意兩個相鄰觸地階段的時間間隔基本相同,因此,除了提取角速度和加速度特征,還可利用時間信息特征來提高零速檢測準確性。為此,本文提出一種基于LSTM網絡的零速檢測方式,利用LSTM不僅可提取角速度和加速度特征,而且能提取零速檢測時序特征,從而提升零速校正算法精度。

1.2 LSTM網絡

長短時記憶網絡是一種特殊的循環(huán)神經網絡(Recurrent Neural Network,RNN)結構,其能很好地解決RNN中梯度消散的問題。該特性使LSTM能保留長期記憶,廣泛用于文本情感分析、語音識別和時序預測等方面[16]。

LSTM與RNN結構基本相同,LSTM采用記憶模塊代替RNN的隱藏單元。LSTM記憶模塊由1個記憶單元和輸入門、輸出門和遺忘門組成。LSTM通過輸入門、輸出門和遺忘門的控制結構實現信息添加與刪除。LSTM記憶單元結構如圖3所示[17]。其中,xt、ht分別表示t時刻的輸入和輸出,σ表示Sigmoid函數,通過與信息進行相乘操作賦予各信息相應權重,從而控制信息。LSTM通過該結構進行長期記憶存儲,在提取數據特征值的基礎上實現對時間序列特征的存儲,從而滿足自適應零速校正算法的需求。

圖3 LSTM記憶單元結構Fig.3 Structure of memory unit in LSTM

1.3 不同運動模式下運動數據特征及數據預處理

本文按照不同運動速度將運動模式分為慢速行走(速度為0.5 m/s～0.9 m/s),中速行走(速度為0.9 m/s～1.3 m/s)和快速行走(速度為1.3 m/s～2 m/s)3組,同時引入行人靜止狀態(tài)作為數據對照,得到的角速度絕對值變化情況如圖4所示。其中,橫實線處角速度絕對值為15,可以看出行走速度越快,步態(tài)周期越短,步頻也越高。當行人為快速行走時,步態(tài)平均周期為0.85 s,步頻為2.35 step/s,單步步長為0.80 m,觸地周期為0.23 s,占整個步態(tài)周期的27.06%,角速度絕對值最大值超過20。當行人為中速行走時,步態(tài)平均周期為1.18 s,步頻為1.69 step/s,單步步長為0.59 m,觸地周期為0.40 s,占整個步態(tài)周期的33.90%,角速度絕對值最大值超過15,但低于20。當行人為慢速行走時,步態(tài)平均周期為1.33 s,步頻為1.50 step/s,單步步長為0.50 m,觸地周期為0.47 s,占整個步態(tài)周期的35.34%,角速度絕對值最大值不超過15。綜上可知,從慢速行走到快速行走,速度越快則步頻越高,單步步長越大,觸地周期越短,觸地周期在整個步態(tài)周期中占比也越小。此外,不同運動模式下除了角速度絕對值最大值及加速度等數值有差異,在時間周期與零速檢測時間上差異也較大,因此,可采用LSTM學習不同運動模式的時序特征。除了時序信息,LSTM的輸入數據還包括x、y、z三軸的角速度數據、加速度數據以及是否為觸地階段等信息。將處于觸地階段的時間點標記為1,處于其他階段的時間點標記為0。通過角速度和加速度數據并結合時序信息來預測該時間點是否處于零速階段,從而實現不同運動模式下零速檢測的自適應判定。

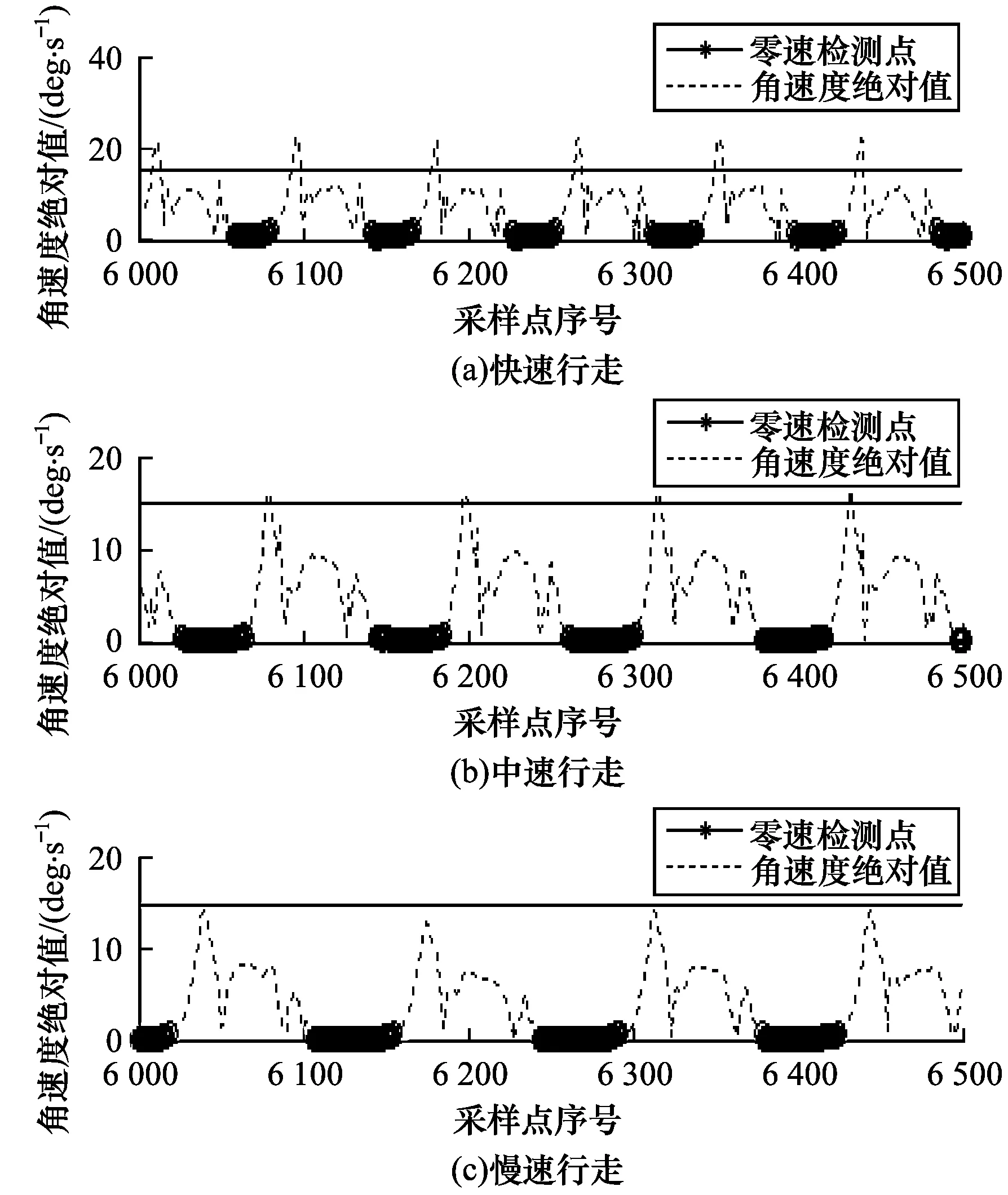
圖4 不同運動模式下角速度絕對值變化Fig.4 Absolute value change of the gyroscope indifferent motion modes

2 累積誤差修正航位推算算法

本文提出基于LSTM算法的零速檢測算法以應對多運動模式下的行人零速檢測問題,然而PDR算法模型與真實人體運動模型存在差異以及行人運動中存在無意識抖動等問題會造成殘余累積誤差,因此,本文采用差分進化算法對殘余累積誤差進行二次修正。

2.1 差分進化算法原理

差分進化算法是一種高效的全局優(yōu)化算法,也是基于群體的啟發(fā)式搜索算法,群體中各個體均對應一個解向量[18]。差分進化算法的進化流程與遺傳算法類似,都包括變異、雜交和選擇操作[19]。在計算過程中,可以假設(a,b,c)為陀螺儀三軸累積偏差值,并用其對陀螺儀偏差值進行修正。

2.1.1 種群初始化

由于(a,b,c)為陀螺儀三軸累積偏差值,因此解空間維數為3,3個偏差值的取值范圍根據經驗值設定為(-0.01,0.01),初始種群的計算公式為:

(1)

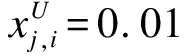
2.1.2 變異操作

隨機選取種群中兩個不同個體,將兩者差值縮放后與另一個體相加,得到:

vi(g+1)=xr1(g)+F×(xr2(g)-xr3(g))

(2)

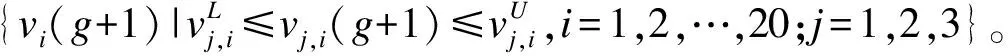
2.1.3 交叉操作

對第g代種群和變異體進行個體間交叉操作如下:

uj,i(g+1)=

(3)

其中,CR為交叉概率,jrand為[1,2,3]的隨機數。為避免中間體無基因遺傳給下一代,在第一個交叉操作中隨機取出vi(g+1)的第jrand位基因作為交叉后個體ui(g+1)對應的基因。

2.1.4 選擇操作

若目標函數f(x)存在f(ui(g+1))≤f(xi(g)),則xi(g+1)=ui(g+1);否則xi(g+1)=xi(g)。當滿足設定條件時,從具有最佳適應性的種群中選擇最佳個體作為解并返回該數值。

2.2 自適應算法

在DE算法中,目標函數的選取是評價種群個體適應性的重要手段。將目標函數的選取結合到PDR算法中,需對慣性導航系統的定位結果做出相應評價,然而因為慣性導航定位算法受累積誤差影響,所以慣性導航定位結果會有較大誤差。因此,需采用UWB、WIFI和藍牙等其他定位方式進行相對準確的絕對定位,將得到的坐標與PDR所得坐標進行對比,從而實現對慣性導航系統定位結果的評價。定位結果的評價指標為均方根誤差(Root Mean Square Error,RMSE),其計算公式如下:

(4)

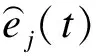
綜上所述,本文所提基于差分進化算法的累積誤差修正航位推算算法流程如圖5所示。

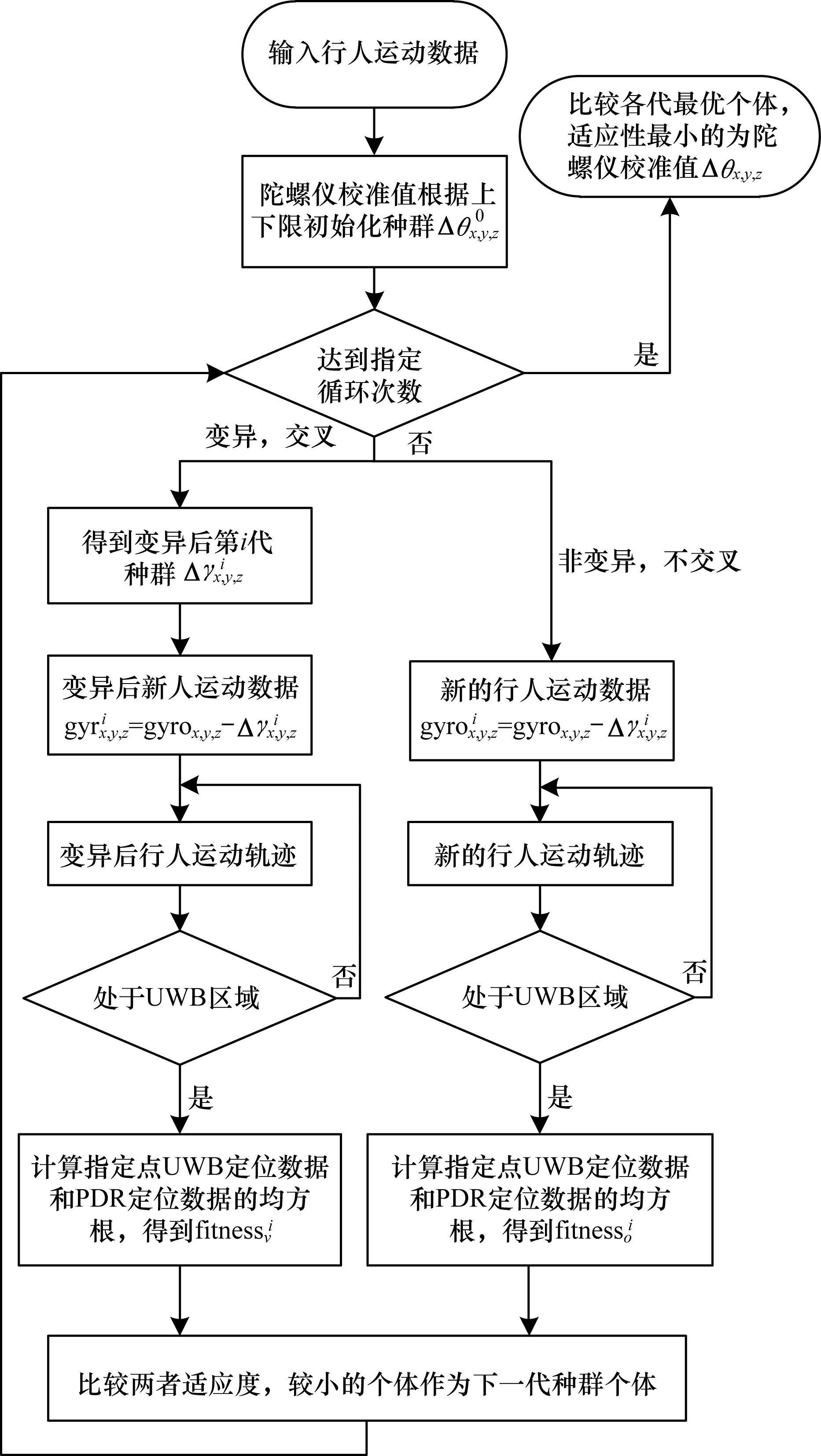
圖5 本文算法流程Fig.5 Procedure of the proposed algorithm

3 實驗結果與分析

本文采用XSENS慣性傳感器模塊分別進行基于LSTM網絡的自適應零速檢測算法實驗與基于DE算法的累積誤差修正算法實驗。

3.1 基于LSTM網絡的自適應零速檢測算法分析

按照不同速度將運動模式分為靜止、慢速行走、中速行走和快速行走4組。實驗人員分別按照上述速度行走(或靜止)60 s,重復10次得到10組不同運動模式的數據,分別去除前后占總數量5%的數據,以避免產生誤差。實驗數據按照是否為觸地階段分別標記為1和0,將所得數據的70%作為訓練集,將其輸入LSTM網絡進行訓練。測試集由以下兩部分組成:

1)剩余30%的數據。將這些數據按照不同運動模式分別輸入網絡進行訓練,評估模型在不同運動模式下的適應性。

2)實驗人員按照靜止、慢速行走、中速行走和快速行走的運動模式(各運動模式時長為10 s),重復采集5組數據,以評估LSTM網絡的自適應零速檢測效果。

表1為不同運動模式下本文算法的檢測準確率、誤判率和漏判率[20]。可以看出,當運動模式為快速行走時,本文算法的檢測準確率比慢速行走和中速行走更高,且誤判率與漏判率更低。這是因為在快速行走過程中,三軸陀螺儀和三軸加速度計所測角速度與加速度數據變化迅速,LSTM網絡能有效提取數據特征,從而提高檢測準確率。在慢速與中速行走過程中,上述數據變化相對緩慢,對準確率的提升有一定影響。綜合來看,在多模式運動過程中本文算法的檢測精度較高,說明LSTM網絡在零速自適應檢測下具有較好的檢測性能。

表1 不同運動模式下本文算法所得實驗結果Table 1 Experimental results of the proposed algorithmin different motion modes %

圖6為多運動模式下采用傳統零速檢測算法(以下稱為傳統算法)與本文基于LSTM網絡的零速檢測算法(以下稱為本文算法)得到的行人運動軌跡。可以看出,在多運動模式(慢速行走、中速行走和快速行走交替進行)下,采用傳統算法固定閾值會造成閾值偏低(或偏高),導致零速校正效果下降,定位結果發(fā)散。采用本文提出的LSTM網絡判定零速區(qū)間可根據不同運動模式自適應調整零速區(qū)間,從而實現對多運動模式下零速區(qū)間的自適應修正。

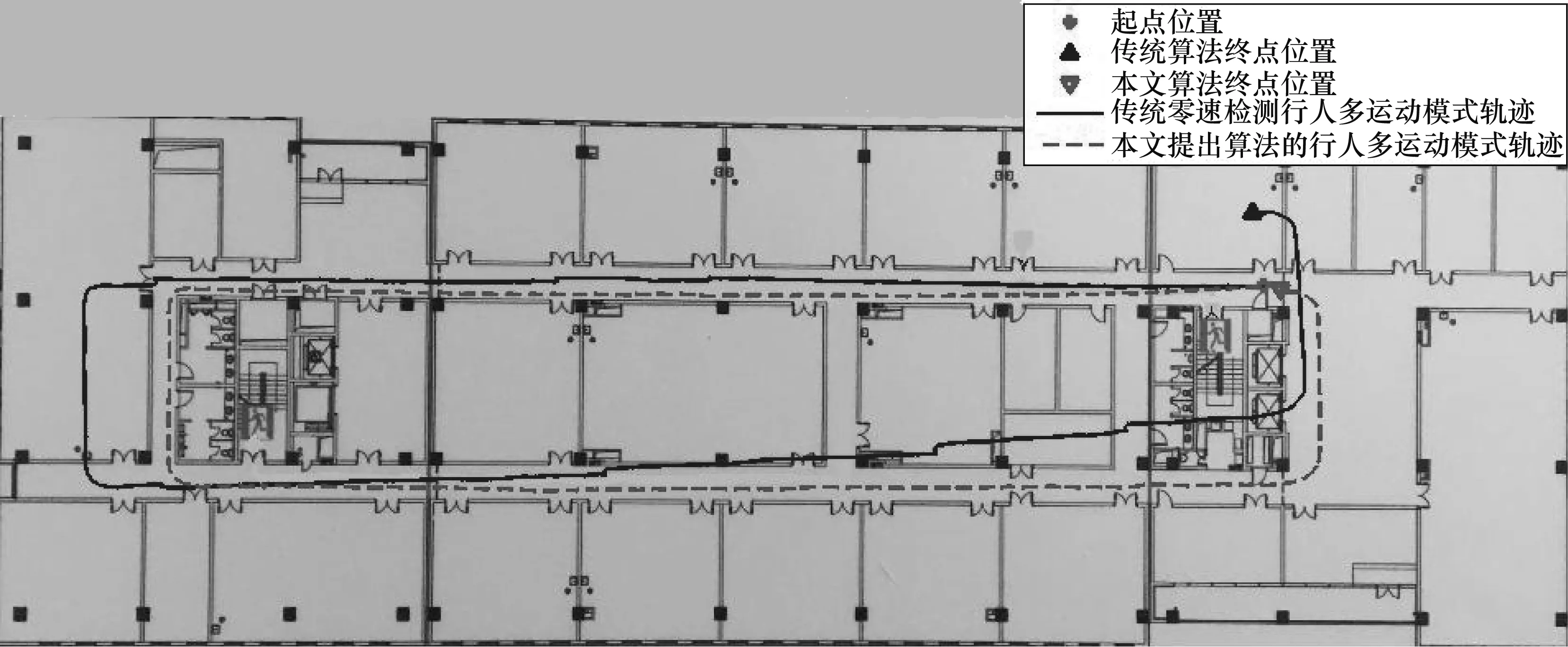
圖6 多運動模式下2種算法所得行人軌跡Fig.6 Pedestrian trajectories obtained by two algorithms in multi-motion mode

3.2 基于DE算法的累積誤差修正算法分析

本文采用DE算法進行累積誤差數據修正的自適應PDR算法關鍵在于UWB、WIFI和藍牙等其他定位方式提供相對精度較高的定位坐標,從而對PDR算法定位結果進行評價,進而實現PDR算法的數據級修正,最終修正累積誤差。

采用UWB定位、WIFI定位和藍牙定位作為輔助定位手段所得本文算法與卡爾曼濾波算法的行人軌跡對比結果分別如圖7～圖9所示。其中,3種定位方式所得傳統卡爾曼濾波算法3次行人距離終點的絕對誤差分別為6.43 m、7.04 m和8.18 m,行走距離分別為516 m、514 m和517 m,相對誤差分別為1.246%、1.370%和1.582%。3種定位方式所得本文算法3次行人距離終點的絕對誤差分別為0.94 m、1.01 m和0.99 m,其相對誤差分別為0.182%、0.196%和0.191%。可以看出,采用DE算法修正陀螺儀誤差后PDR算法的誤差大幅減小,本文算法對不同定位方式具有較好的適應性。

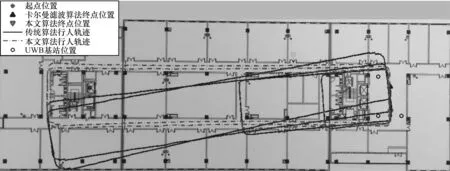
圖7 采用UWB定位輔助所得2種算法的行人軌跡對比Fig.7 Comparison of pedestrian trajectories between two algorithms aided by UWB location

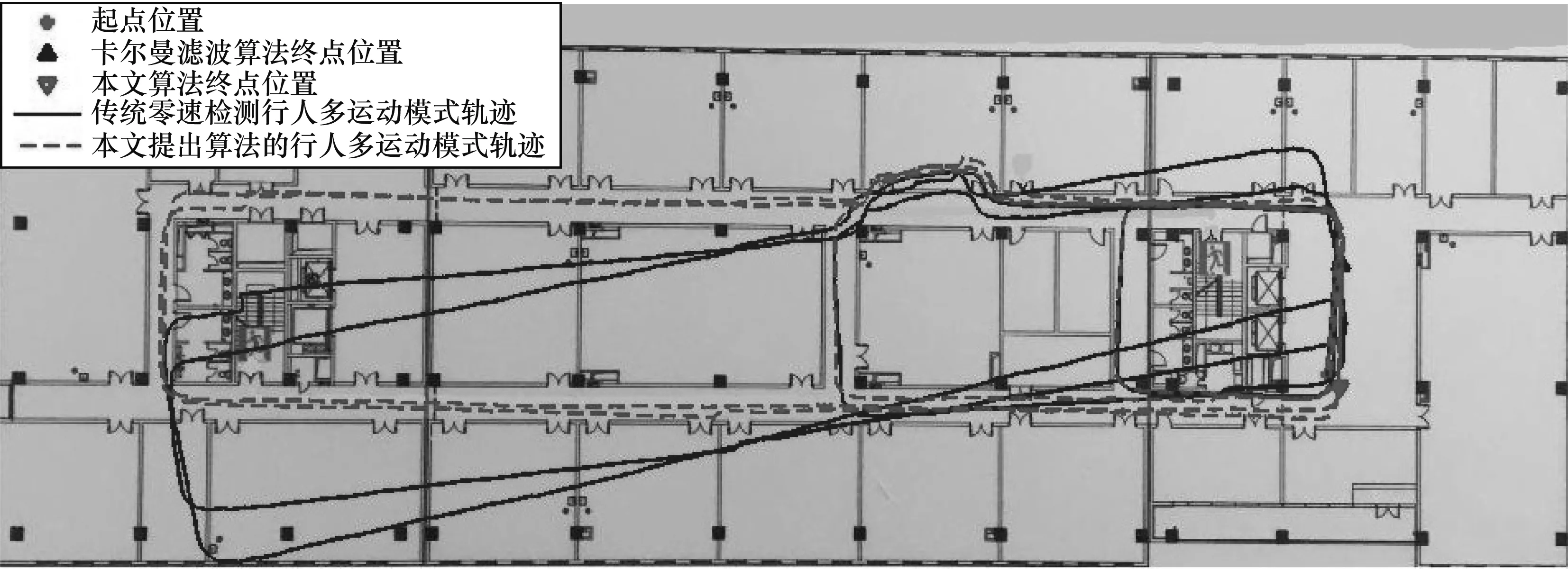
圖8 采用WIFI定位輔助所得2種算法的行人軌跡對比Fig.8 Comparison of pedestrian trajectories between two algorithms aided by WIFI location

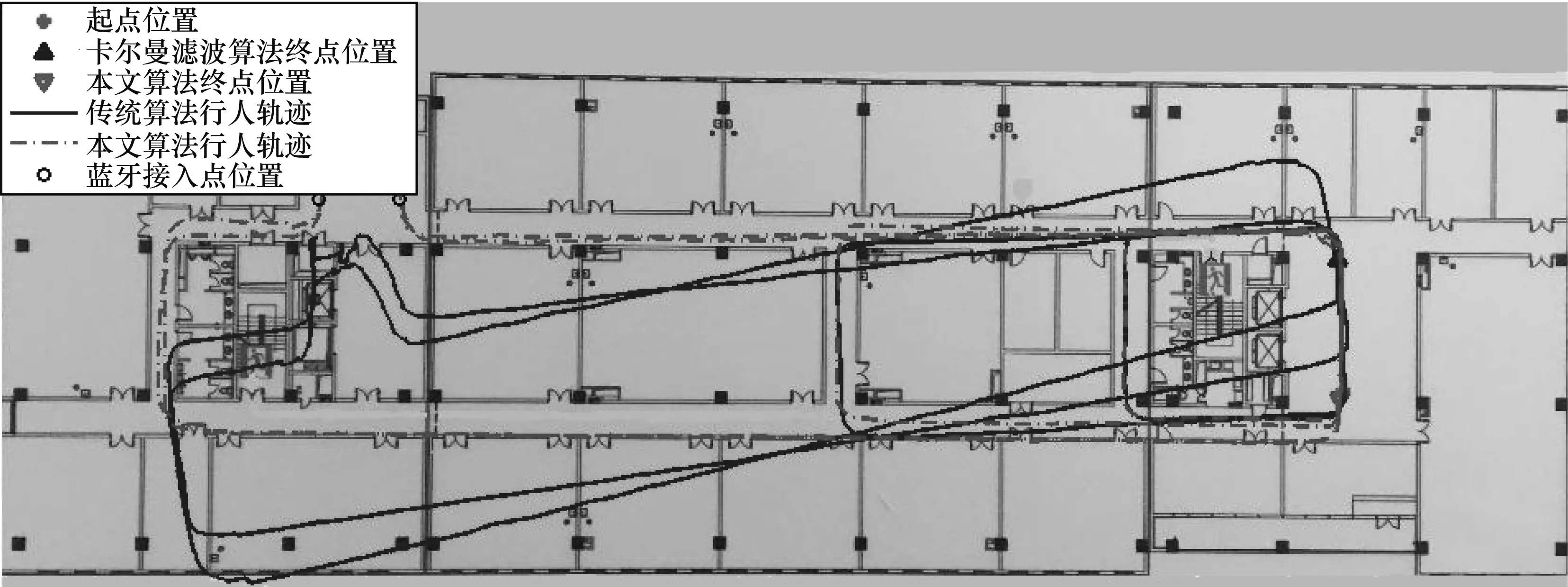
圖9 采用藍牙定位輔助所得2種算法的行人軌跡對比Fig.9 Comparison of pedestrian trajectories between two algorithms aided by Bluetooth location

為進一步驗證本文所提算法的有效性與穩(wěn)定性,獨立重復10次上述實驗且每次在行走距離為52 m、145 m、327 m和516 m處適當停頓。將10組實驗所得終點絕對誤差的平均值作為最終絕對誤差,將所得相對誤差的平均值作為最終相對誤差,以減小實驗結果的偶然性,實驗結果如表2所示。

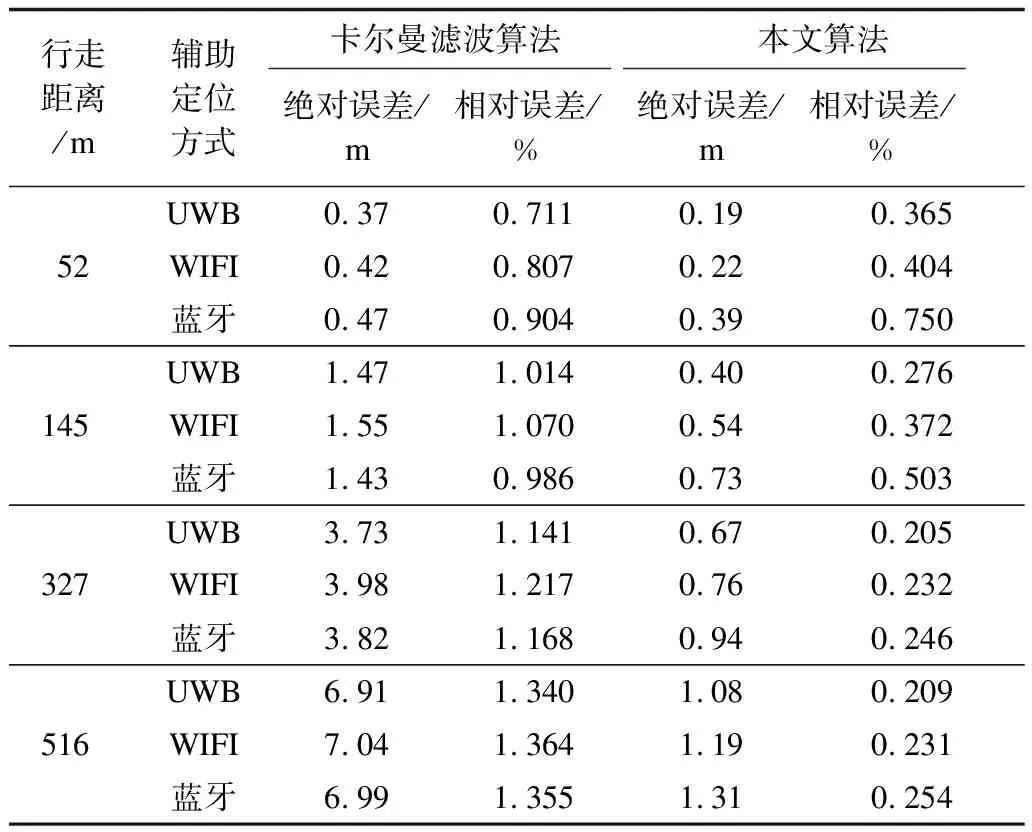
表2 3種定位方式輔助下2種算法不同行走距離的誤差統計結果Table 2 Error statistical results of two algorithms in differentwalking distances aided by three positioning methods

可以看出,卡爾曼濾波算法所得絕對誤差和相對誤差均隨著行走距離的增大而增加,且行走距離越大增幅越大。從相對誤差的變化趨勢可知,定位精度隨著行走距離的增大而降低,且行走距離越大降幅越大。而本文算法的絕對誤差雖然隨著行走距離的增大而增加,但增幅相對穩(wěn)定,且從相對誤差整體變化情況來看,本文算法可有效抑制相對誤差的發(fā)散。

從不同的輔助定位方式來看,本文算法對不同定位方式具有良好的適應性,可有效減少定位結果偏差,提高定位精度。從定位效果來看,UWB、WIFI和藍牙的定位效果逐漸減弱,這可能是因為UWB的室內定位抗多徑干擾能力強,能有效對慣性導航定位算法的計算數據進行修正,減少累積誤差。藍牙抗干擾能力最弱,對數據修正不足,存在較多累積誤差。

由上述可知,本文算法能較好的適應其他定位手段,可通過修正陀螺儀的偏移數據有效減小累積誤差,提高定位精度,但其所用計算時間較卡爾曼濾波算法也更長,卡爾曼濾波算法用時約5 s,本文用時約47.6 s。

4 結束語

本文針對多運動模式下零速校正困難的問題,提出一種基于LSTM網絡的零速判定算法。根據不同運動模式自適應調整零速檢測范圍,實現多運動模式下的零速檢測。在此基礎上,設計基于DE算法進行數據修正的融合PDR算法,用其分析定位結果并在UWB、WIFI和藍牙等定位方式下對本文算法效果進行驗證。實驗結果表明,該算法較卡爾曼濾波算法的絕對定位誤差與相對定位誤差更小,有效抑制了誤差發(fā)散。然而該算法在運行速度以及場景泛化上存在一定局限性,下一步將優(yōu)化DE算法加快運行速度,同時考慮在運動中進行UWB和IMU數據耦合以提高算法在不同場景下的應用性。