污水處理廠剩余污泥理論估算與實際產量的比較

金平日，顧雪鋒，汪玉平

(北控水務<中國>投資有限公司，浙江杭州 311100)

目前，我國對剩余污泥產量的研究較少，尚未形成適合我國各地區水質特點的統一方法。近年來，污泥處理處置已成為我國污水處理廠的重大難題[1]。研究污泥產量，以提高污水廠污泥產量預測的準確性及污泥處理系統設計的科學性十分必要[2]。一方面，污泥產量的預測影響污水廠的運行成本，從而影響污水處理費單價；另一方面，污泥產量的預測結果會直接影響污泥脫水系統的設計，若設計能力過小，則污泥處理系統無法正常運行，影響污水廠出水水質；設計能力過大，則會造成資源浪費。

剩余污泥是污水生化處理系統產生的污泥，一般占全廠污泥總量的90%以上。對剩余污泥量的準確預測有助于污泥處理系統的設計。陳曉光等[3]提出了基于IWA污泥產率的修正公式，指出剩余污泥中進水惰性SS(suspended solid)沉積量占比較大，進水中揮發性懸浮顆粒物所占比例(fv)污泥產率影響較大。譚學軍等[4]根據活性污泥微生物增殖公式，推算了污泥合成產率和衰減系數，為準確計算污泥量提供了條件。高靜等[5]通過對生產運行和化驗數據分析，在德國ATV標準推薦的污泥產率公式的基礎上，增加了修正系數K，提高了其準確性。

本文通過對我國《室外排水設計規范》(GB 50014—2006)(以下簡稱《規范》)中剩余污泥量計算公式的分析，對比山東某地區3個污水處理廠實際污泥產量數據，以新角度對污泥產量預測的方法進行了闡釋。

1 剩余污泥計算公式分析

我國《規范》中采用的剩余污泥產量計算如式(1)。

ΔX=YQ(S0-Se) -KdVXv+fQ(SS0-SSe)

(1)

其中：ΔX——每日產生的剩余污泥量，kg SS/d；

V——生物反應池容積，m3；

Y——污泥產率系數，kg VSS/(kg BOD5)，在溫度為20 ℃時，取值為0.3～0.8；

Q——設計日平均污水量，m3/d；

S0——進水五日生化需氧量，kg/m3；

Se——出水五日生化需氧量，kg/m3；

Xv——生物反應池內混合液揮發性懸浮固體平均濃度，g MLVSS/L；

f——SS的污泥轉換率，一般取值為0.5～0.7；

SS0——進水懸浮物濃度，kg/m3；

SSe——出水懸浮物濃度，kg/m3；

Kd——衰減系數。

衰減系數Kd受溫度影響，其計算如式(2)。將式(2)帶入式(1)得出式(3)。

KdT=Kd20(θT)T-20

(2)

ΔX=YQ(S0-Se)-Kd20(θT)T-20VXv+fQ(SS0-SSe)

(3)

其中：KdT——溫度為T時的衰減系數；

K20——20 ℃時的衰減系數，一般取值為0.04～0.075[6]；

T——溫度，℃；

θT——溫度系數，一般取值為1.02～1.06[6]。

可見，各參數的取值范圍較寬泛，在實際產泥量預測中，參數選取困難，且在實際設計過程中，為考慮設計的合規性，很少采用規范以外的計算模型作為設計基礎。因此，分析各參數對產泥量的影響，即進行各參數的敏感性分析，對污泥產量預測意義較大。

2 分析方法

首先對水廠A的產泥量進行研究，初步分析理論產泥量與實際產泥量的差異，再利用其他2個水廠的現場運行數據，對初步分析的結論進一步論證。分析基礎為現場實際運行數據，包括其工藝參數、進出水水質及產泥量等，利用IBM SPSS Statistics 23進行統計分析。

3 參數敏感性分析

為簡化分析過程，采用單因素敏感性分析方法，分析各參數對產泥量的影響，并按實際設計工作中的參數取值習慣選取參數區間間隔。初始值均采用最低值，即Y=0.3、Kd20=0.04、θT=1.02、f=0.5，進水BOD5為140 mg/L，出水BOD5為10 mg/L，進水SS為170 mg/L，出水SS為10 mg/L，揮發性污泥濃度(MLVSS)為2.1 g/L，好氧區停留時間為9 h。水量以6.0萬t/d作為測算基礎，則初始泥量為7.14 t/d。單因素敏感性分析如式(4)。

(4)

其中：α——代表性字母，代表式(3)中采用的參數(Y、Kd20、θ、f)；

ΔX1——參數α在α1時得出的產泥量；

ΔX2——參數α在α2時得出的產泥量。

敏感度系數越高，該參數對產泥量影響越大，具體如表1所示。

表1 產泥量公式參數的單因素敏感度分析Tab.1 Single Factor Sensitivity Analysis of Parameters of Theoretical Sludge Production

由表1可知，污泥產率系數Y的敏感度系數為8.4，懸浮物轉換系數f的敏感度系數為9.6，而衰減系數Kd與溫度系數θ的敏感度則相對較弱，分別為0.01左右及0.052。

結合式(3)可知，敏感度系數與BOD及SS有關，即污泥產率的敏感度系數與BOD關系較大，而SS轉換率的敏感度系數與SS濃度成正相關。

敏感度系數分析只能代表該條件下敏感度系數的大致范圍，并不能一一相互比較。但表1的結果表明，影響污泥產量程度較大的是污泥產率系數Y及SS轉換率f，這些參數的取值在實際設計過程中應尤為慎重。

4 線性回歸分析

為進一步研究理論產泥量與實際產泥量之間的關系，利用線性回歸分析方法，按《規范》中理論計算公式對污水廠A的實際產泥量進行了擬合。

周雹[6]認為，產泥系數Y的選擇需考慮COD/BOD，當COD/BOD > 2.2時，則應以COD為計算基礎；當COD/BOD < 2.2時，需以BOD為計算基礎。污水廠A的COD/BOD約為2.95。因此，以COD作為計算基礎，并進行分析，擬合結果如表2～表4所示。

表2 污水廠A線性回歸分析總表(I)Tab.2 Linear Regression Analysis of WWTP A(Ⅰ)

表3 污水廠A線性回歸分析總表(II)Tab.3 Linear Regression Analysis of WWTP A(Ⅱ)

表4 污水廠A線性回歸分析總表(III)Tab.4 Linear Regression Analysis of WWTP A(Ⅲ)

由R=0.994可知，線性回歸效果較好，但依據回歸結果中的參數，則可得Y=0.095、Kd20×(θT)(T-20)=-0.152、f=0.072，將上述參數代入式(3)，則計算如式(5)。

ΔX=0.095Q(S0-Se)+0.152VXv+
0.072Q(SS0-SSe)

(5)

這與規范中或理論推算結果相差甚遠。

為進一步驗證此結果，對污水廠A的2018年全年實際產泥量、《規范》計算理論產泥量及擬合后的預測產泥量進行了對比分析，結果如圖1所示。

為使《規范》預測的產泥量趨于實際產泥量，經測試不同參數取值后，確定為Y=0.9、Kd=0.04、θ=1.02，f=0.5。但《規范》公式的結果與實際產泥量

圖1 污泥模擬產量與實際產量對比曲線Fig.1 Comparison of Simulated and Actual Production of Sludge

差距較大，而擬合曲線卻更趨近于實際產泥量。

為避免結果的偶然性，選取山東另2個污水廠，即污水廠B和污水廠C的日運行數據作為分析基礎，進行并列分析。

B水廠采用AAO工藝，平均處理水量為5.43萬t/d，好氧區停留時間為11 h，其平均進出水水質如表5所示。

表5 B水廠進出水水質Tab.5 Influent and Effluent Water Quality of WWTP B

C水廠也采用AAO工藝，平均處理水量為10.58萬t/d，好氧區停留時間為10 h，其平均進出水水質如表6所示。

表6 C水廠進出水水質表Tab.6 Influent and Effluent Water Quality of WWTP C

將B水廠與C水廠分別進行分析。由表7～表9和圖2可知，B水廠的COD去除量和SS去除量對產泥量的影響較大，而污泥衰減部分對產泥量影響較小，但優化后的《規范》產泥量依然與實際產泥量相差較大，這與A水廠的情況有所不同。

表7 污水廠B線性回歸分析(Ⅰ)Tab.7 Linear Regression Analysis of WWTP B(Ⅰ)

C水廠的擬合結果，如表10～表12和圖3所示，R在0.9以上。

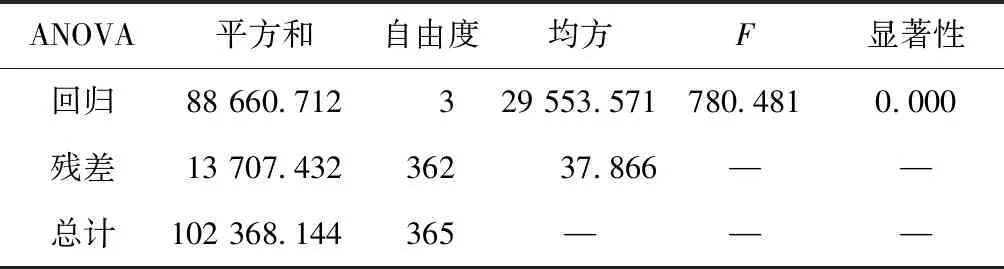
表8 污水廠B線性回歸分析(Ⅱ)Tab.8 Linear Regression Analysis of WWTP B(Ⅱ)

與污水廠B類似，《規范》產泥量高于實際產泥量，而擬合計算的產泥量則更趨于穩定。污水廠C的SS去除量對產泥量存在較大影響，而污泥衰減部分和COD去除量對其產泥量影響較小，與污水廠B的情況存在差異。

表9 污水廠B線性回歸分析(Ⅲ)Tab.9 Linear Regression Analysis of WWTP B(Ⅲ)

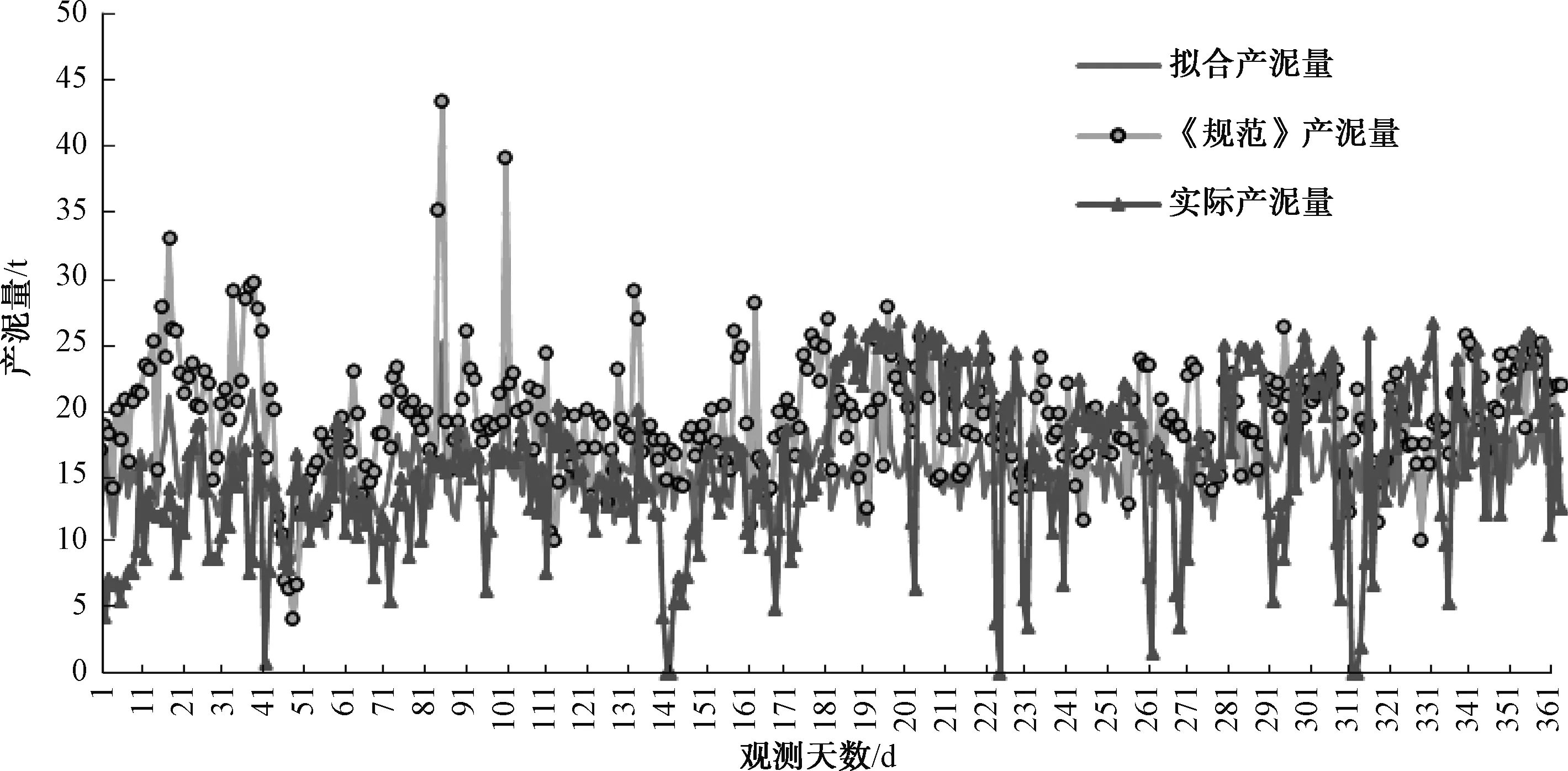
圖2 水廠B的計算與實際產泥量比較Fig.2 Comparison of Simulated and Actual Sludge Production of WWTP B

表10 污水廠C線性回歸分析(Ⅰ)Tab.10 Linear Regression Analysis of WWTP C(Ⅰ)

表11 污水廠B線性回歸分析(Ⅱ)Tab.11 Linear Regression Analysis of WWTP B(Ⅱ)

表12 污水廠B線性回歸分析(Ⅲ)Tab.12 Linear Regression Analysis of WWTP B(Ⅲ)

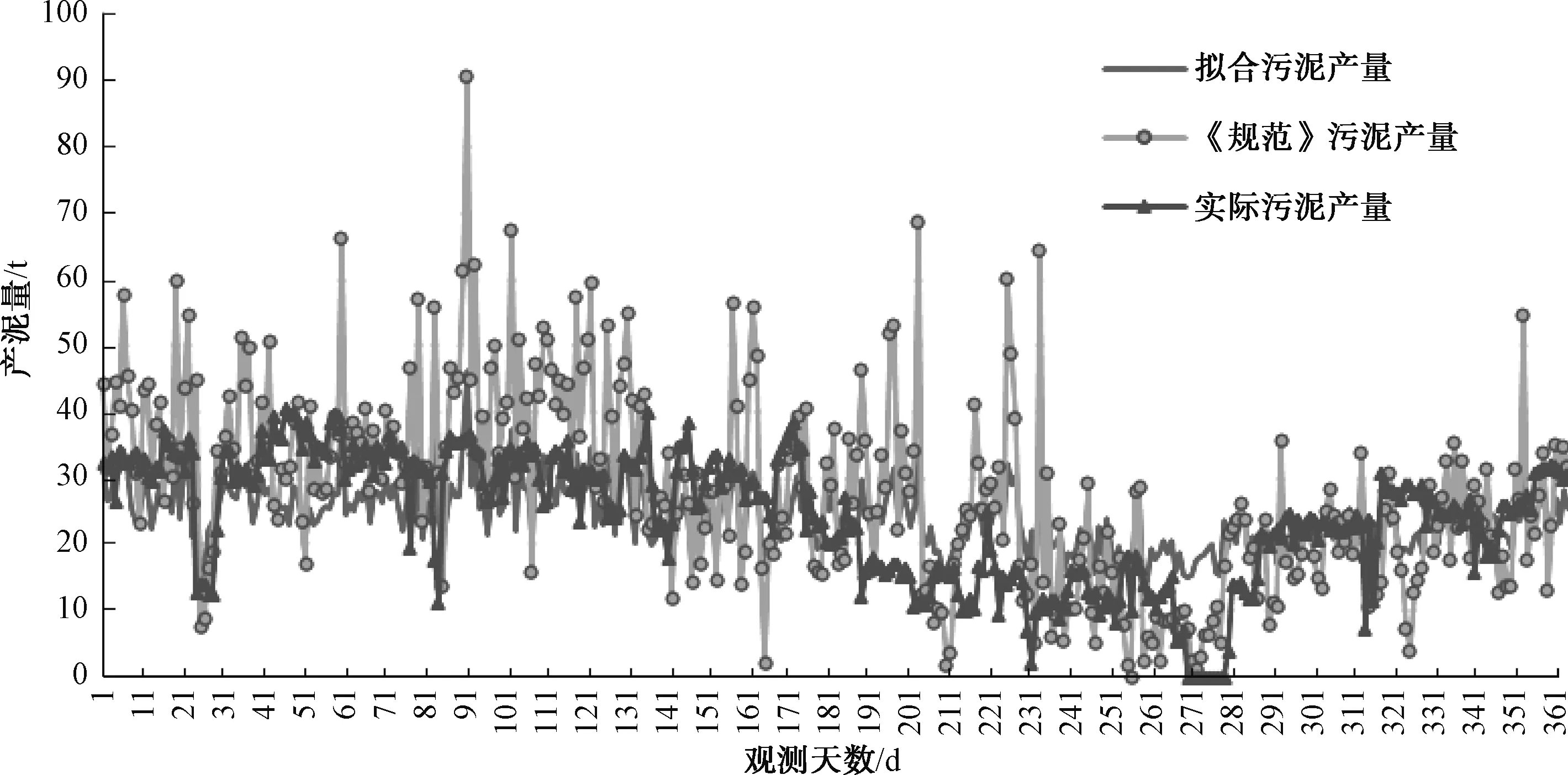
圖3 水廠C的計算與實際產泥量比較Fig.3 Comparison of Simulated and Actual Sludge Production of WWTP C

5 結果與討論

本文選取了山東某地區的3個污水廠作為研究對象，以3個污水廠的日運行數據作為分析基礎，比較分析了理論產泥量和實際產泥量的差異。結果表明，在理論計算中，污泥產率系數Y及SS轉化系數f對污泥產量影響較大。但實際運行數據的分析結果表明，污水廠A系統中揮發性污泥總量對產泥量有較大影響，污水廠B中的SS去除量和COD去除量對產泥量存在較大影響，而污水廠C的產泥量則更多取決于SS去除量。利用《規范》中的參數及變量，無法準確預測實際產泥量，甚至在同一地區，其參數及影響產泥量的變量也存在較大差距。

因此，若僅依據《規范》中的計算方法進行產泥量預測，將與實際產泥量存在較大差異?！兑幏丁分挟a泥量的計算，以微生物動力學為基礎，以生物系統穩定、進水水量水質穩定，并以忽略運行人員操作能力對系統的影響，且微生物增長速率及衰減速率均符合相應理論等情況為前置條件。實際運行中，進水普遍含有一定比例的工業污水，污泥產量不僅取決于生物系統，更取決于進水波動、污水廠運行習慣、化驗數據的滯后性及準確性等諸多因素。Jung等[7]認為，即使進水相同、池容相同，但厭氧環境和好氧環境頻繁交替時，也會影響污泥產量。

6 結論

本次研究發現，實際運行過程中，可在長期數據積累的基礎上，對相應計算模型進行擬合及回歸分析，找出各污水廠的“特征”參數，作為指導日常運行的依據，以保證污水處理系統的穩定性。

基于不同數學模型，所采用的參數估計方法也有所不同。《規范》中采用的數學模型較為簡單，變量較少，需采用統計學估計的系數較少，便于現場人員操作。因此，建議依然采用《規范》中建議的變量及邏輯，即COD或BOD的變化量、SS去除量、污泥衰減量等變量，并利用水廠運行數據進行線性擬合，找出水廠特征系數，后按此特征系數靈活調整排泥量及其他運行內容。

在缺少相關數據情況下，進行污泥系統設計時，應參考周邊或類似地區的運行特點及相關數據作為參考，并進行相關試驗作為設計基礎，而非簡單套用《規范》中的相關公式。