典型激勵方式對船舶結構振動聲輻射的影響

宋 超，趙 巖，劉江濤，張乾坤，高 聰

(1.海軍裝備部裝備項目管理中心，北京 100071；2.中國艦船研究院，北京 100192；3.哈爾濱工程大學，黑龍江 哈爾濱 150001)

0 引 言

船舶結構在機械設備不平衡激擾力和不平衡激擾力矩作用下，會產生多種形式的振動，從而引起結構向外輻射噪聲，不僅對船舶聲學性能產生負面影響，而且對船載機械設備的正常運行以及人員的舒適性帶來極大威脅[1–3]。

船舶結構振動聲輻射特性與其所受到的激勵載荷密切相關，如何明確設備對船舶結構的激勵載荷輸入[4]與減小船舶結構振動聲輻射一直以來都是國內外研究人員著力解決的問題[5–7]。早期專家學者對機械設備結構振動特性的分析，大多是采用互易原理和等效力方法經測量換算后獲得的[8–10]。隨著研究的深入，逐漸采用設備輸入到船體結構的功率來表示機械設備結構振動特性的基本參數[11–12]。王振鴻[13]系統介紹了船舶結構中能量的傳遞以及設備激振力獲取的問題。俄羅斯中央科學研究院[14]建立了“設備—隔振器—基座結構”強迫振動系統的一般求解方程，形成了分析系統激勵載荷的理論。馬建強[15]等采用數值方法分析了典型船舶基座結構的阻抗特性，并研究了基座結構參數與結構形式對艙段聲振特性的影響，

綜上所述，目前國內外所進行的研究工作大多數只是探究了在單一載荷形式對于船舶結構振動聲輻射特性的影響，一定程度上忽略了船舶結構振動聲輻射特性與激勵載荷形式因素之間的關系，因此本文將開展在設備不平衡激擾力、不平衡激擾力矩、不平衡激擾力與力矩聯合作用下船舶結構振動聲輻射特性分析，并歸納總結不同激勵載荷對于船舶結構振動聲輻射的影響。

1 船舶結構振動聲輻射理論分析

1.1 聲固耦合理論基礎

船舶結構振動產生的聲輻射聲場與船舶結構之間相互耦合，這種耦合作用相比空氣噪聲源與空氣的耦合作用更為復雜，所以針對船舶這種大型復雜結構且考慮到船舶振動多是低頻激勵源，有限元/邊界元法是較適合解決船舶結構振動聲輻射的方法。聲固耦合有限元法計算船舶結構振動聲輻射計算流程如圖1 所示。

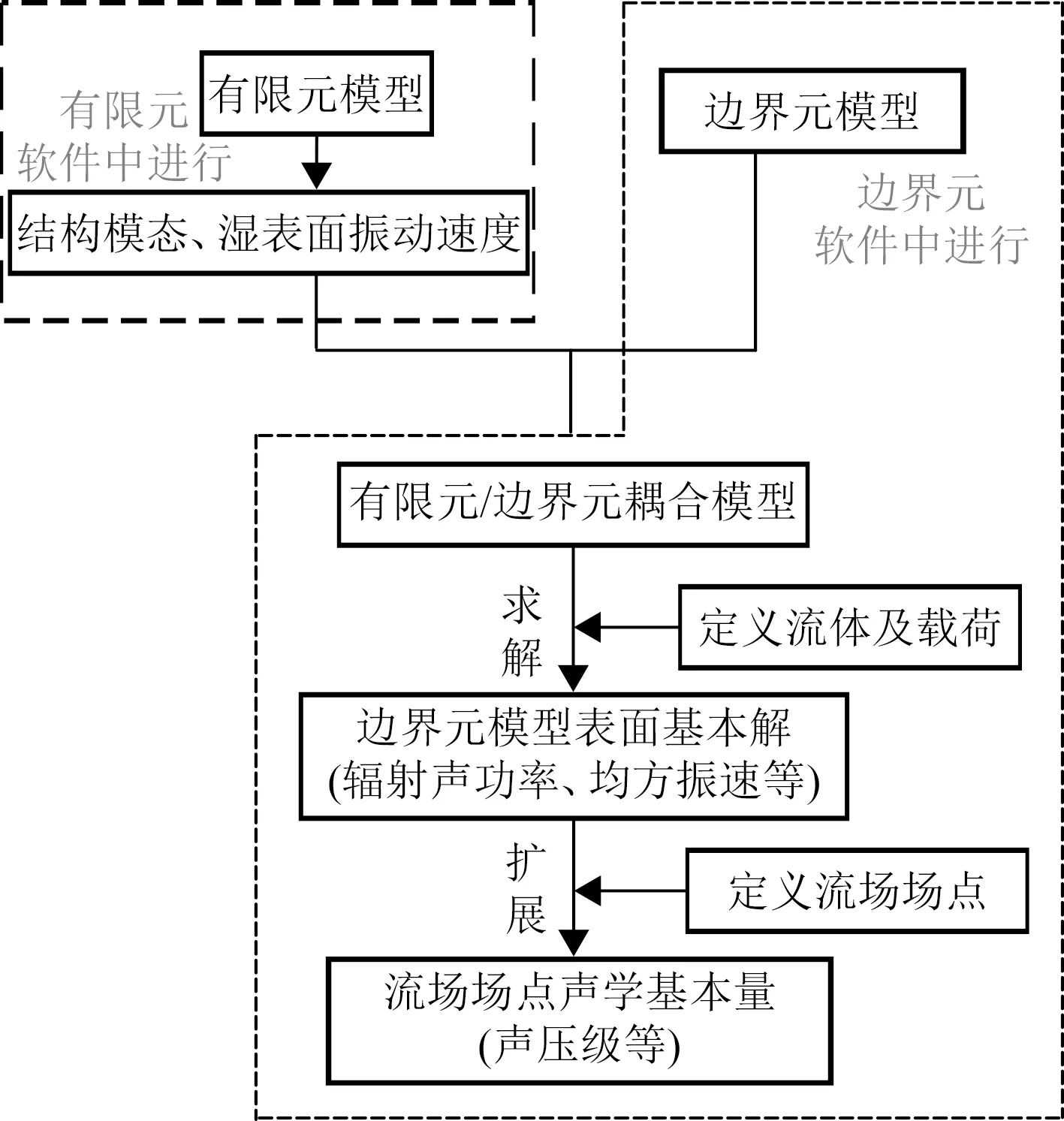
圖1 聲固耦合有限元法計算流程圖Fig.1 Acoustic-structure coupling finite element method calculation flowchart

假定流體為理想聲學介質，流場中聲波的波動方程為：

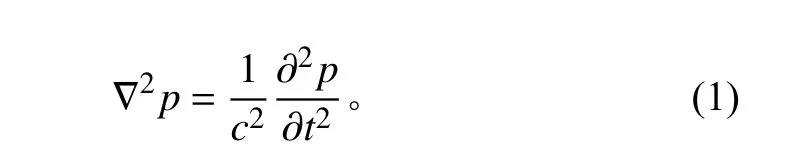
其中：p 為瞬時聲壓；t 為時間；c 為聲速； ?2為拉普拉斯算子。

約去聲壓變分，得到流體區域內聲場的有限元方程矩陣如下：

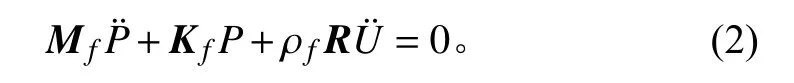
式中： Mf為流體等效質量矩陣； Kf為流體等效剛度矩陣； R為流體和結構耦合矩陣； P為節點聲壓矩陣；為聲壓的2 階導數； U¨為位移的2 階導數。

當考慮在流體區域邊界Σ 上和流體與船體結構的交界面S 上有阻尼吸聲材料時阻尼時，矩陣方程式為：

式中： Cf為聲阻尼矩陣。

類似的，有結構阻尼艙段結構振動的有限元方程為：

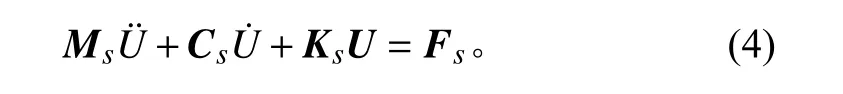
式中： Ms為 船舶結構的質量矩陣； Ks為船舶結構的剛度矩陣； Cs為 船舶結構的阻尼矩陣； Fs為船舶結構載荷力向量。

船舶結構與聲場耦合振動矩陣方程為：

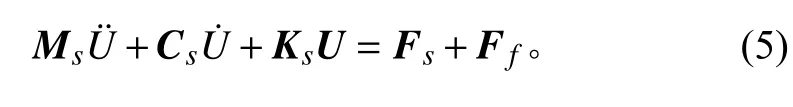
式中： Ff=RTP。

將以上兩式聯立得：

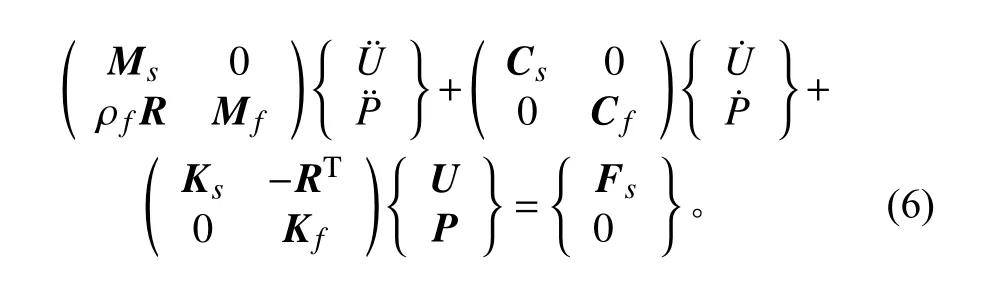
根據上式，可以得到船體結構表面節點處的位移和聲壓，當流場邊界無聲波反射時，可以看作無限流體域結構與流體的耦合振動和聲輻射問題。

1.2 船舶結構分析模型建立

1.2.1 艙段結構基準模型選取

綜合考慮本文研究目的旨在探索不同類型激勵載荷作用下結構振動聲輻射特性規律，因此設置本文研究目標模型為某船舶典型機艙艙段結構。艙段模型幾何尺寸為4×2.4×2 m，舷側艙壁結構沿縱向布設有7 根加強筋，相鄰加強筋間距0.5 m，舷側艙壁結構沿縱向布設有7 根加強筋，相鄰加強筋間距0.5 m，肋骨選用尺寸0.14×0.12×0.008×0.01 m T 型材，艙壁厚度為0.01 m；艙室上甲板與艙室內底板同樣布設有加強結構，頂部肋板2.1×0.006×0.1 m，底部肋板1.8×0.008×0.2 m；基座安裝在艙室底板的局部式基座，屬水平方向上的中央位置，主要由面板、腹板及肘板組成，艙段結構原模型的基座結構面板厚度0.006 m、腹板厚度0.006 m、肘板厚度0.006 m。

1.2.2 聲固耦合分析模型建立

在開展艙段結構振動特性分析之前，首先建立內外流場，定義物理屬性，然后根據計算的頻率范圍確定流場單元尺寸，最后將結構和流場之間相互耦合。為保證計算結果的正確性，在板架結構中一個波長范圍內必須包含至少4～5 個節點，可以根據下式確定最大網格尺寸。

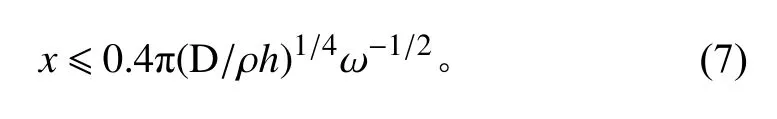
基于上述理論，建立船舶典型艙段結構有限元分析模型，結構網格尺寸λ=0.04m。結構面單元數46000個，有限元模型單元總數46000 個，邊界元模型單元總數5000 個，如圖2 所示。

圖2 艙段結構基準模型有限元/邊界元模型Fig.2 Finite element/boundary element model of cabin structure benchmark model

2 不同激勵載荷對船舶結構振動聲輻射影響

船用機械設備按照振動機理不同，可分為往復類、旋轉類及流體動力類等，有些設備在運行過程中會產生不平衡激擾力或不平衡激擾力矩，如推進電機、汽輪發電機等設備。因此本文在分析設備對安裝基礎激勵特性的過程中，分為設備不平衡力單獨作用，設備不平衡激擾力矩單獨作用以及聯合作用3 種工況分別進行討論。考慮到機械設備產生的激振載荷主要處于低頻段，所引起結構輻射噪聲也主要處于低頻范圍，因此計算頻段選定為1～200 Hz。

2.1 設備不平衡力激勵作用

2.1.1 設備對基座激勵力分析

設備對安裝基礎的激勵載荷與設備自身以及安裝方式密切相關，為便于研究，采用常見安裝方式即設備通過隔振器與基座相連接的方式，分析基座所受到的激勵載荷。

當僅有不平衡激擾力作用在設備上時，設備-基座耦合模型簡化為一維振動模型，如圖3 所示。

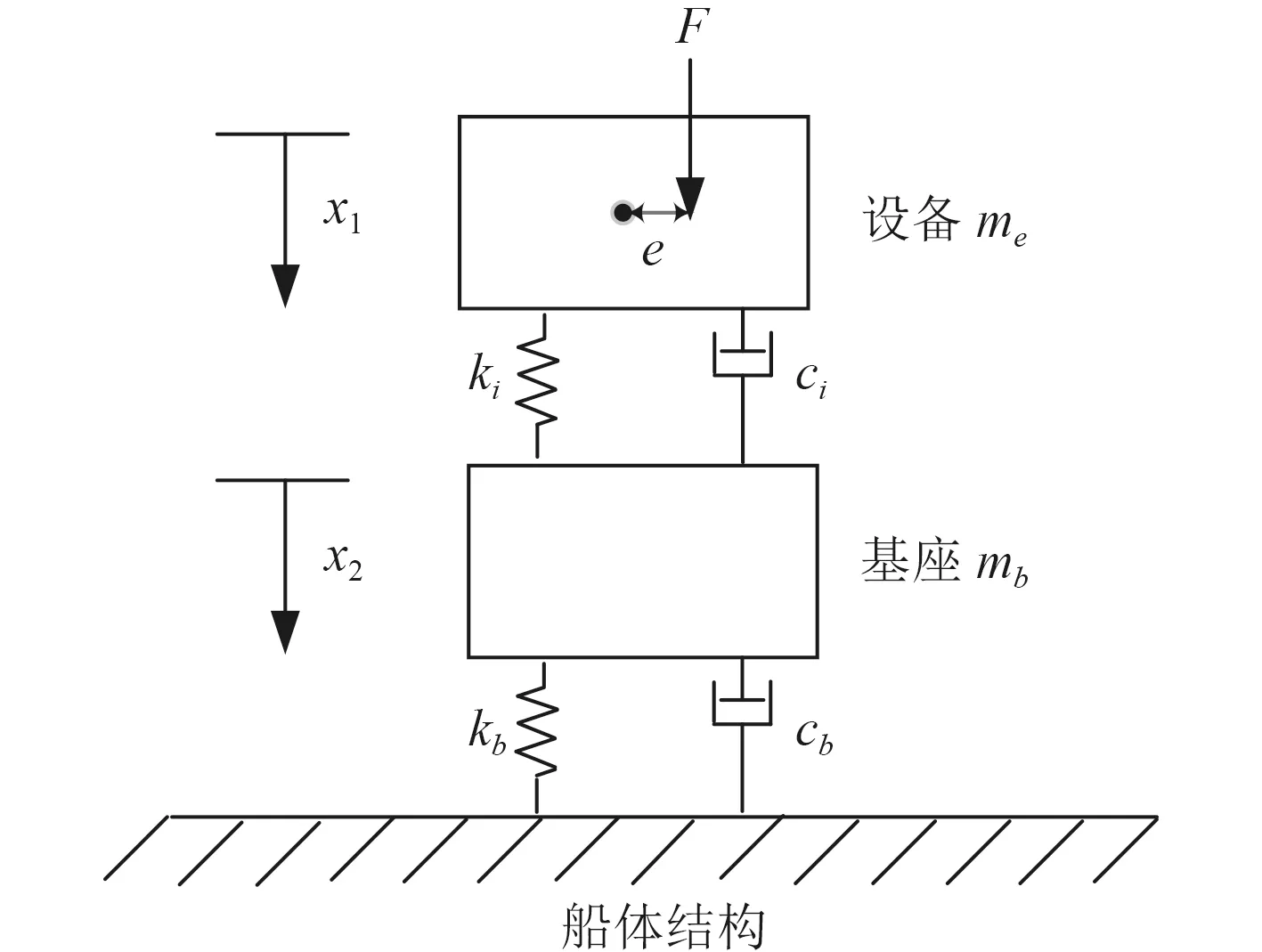
圖3 不平衡力作用下設備與基座耦合模型圖Fig.3 Coupling model diagram of equipment and base under unbalanced force

根據強迫振動理論[16]，不平衡激擾力單獨作用情況下的振動系統的運動方程為：

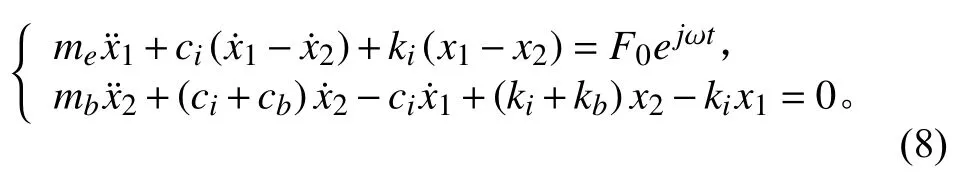
經求解，基座受到的激勵載荷為：

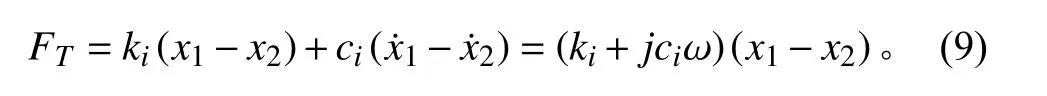
2.1.2 不平衡力作用下結構振動聲輻射特性

如果設備主要因為自身不平衡力產生對外部的激勵，此設備自身的不平衡力既有垂向力（垂直于基座面板）又有水平力，且兩者幅值大小相當。因此在分析設備不平衡力作用下，在設備質心處施加垂向與水平方向單位力，艙段結構在不平衡力作用下振動聲輻射計算結果如圖4 所示。

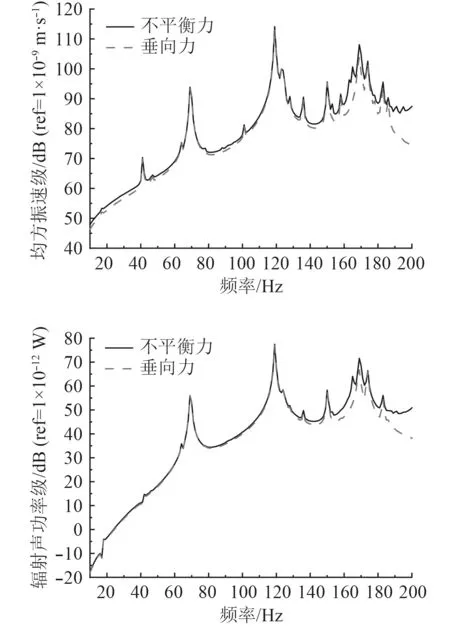
圖4 不平衡力作用下艙段結構振動聲輻射特性Fig.4 Vibration and sound radiation characteristics of cabin structure under unbalanced force

可以看出，艙段結構在不平衡激振力載荷作用下相應曲線趨勢與垂向力作用下響應曲線趨勢基本一致，振動峰值所對應的頻率基本相同，且在所計算頻段范圍內，只考慮垂向力的計算結果與不平衡力計算結果在大多數頻點處響應值相差3 dB 以內，由此可知，不平衡力作用下，垂向載荷起到主導作用。隨著頻率的升高，振動頻譜特性更加豐富，小的振動峰出現頻率增大。部分典型振動峰值頻率下結構振型圖如圖5 所示。

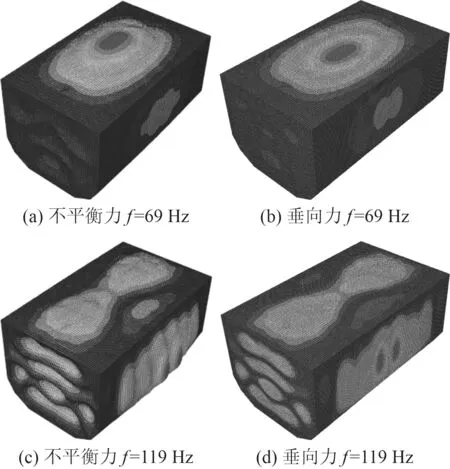
圖5 峰值頻點處振動響應云圖對比Fig.5 Contrast of vibration response cloud images at peak frequency points

由結構振動位移響應云圖可以發現，69 Hz 時結構振型均表現為甲板結構的1 階振動，119 Hz 處表現為甲板2 階振動，側面艙壁主要表現為板格中心振動，隨著頻率的升高，結構主要表現為板格中心振動。

2.2 設備不平衡力矩激勵作用

2.2.1 設備對基座激勵力分析

當設備受到不平衡激擾力矩作用時，設備-基座耦合振動系統會出現平面內扭轉運動，因此基座受到的載荷會發生相應改變。

假設設備的不平衡激擾力矩的作用點為設備的質心，隔振器對稱布置在設備幾何中心兩側；由于設備將發生扭轉振動，兩側基座受到的激勵大小不同，因此分析模型分為左右兩基座進行討論，耦合振動系統計算模型如圖6 所示。

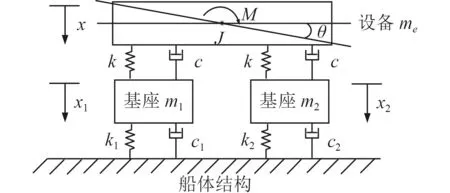
圖6 不平衡力矩作用下設備與基座耦合模型圖Fig.6 Coupling model diagram of equipment and base under unbalanced moment

對設備與基座聯立振動方程組，則設備通過隔振器向安裝基礎所傳遞的激勵力可表示為：

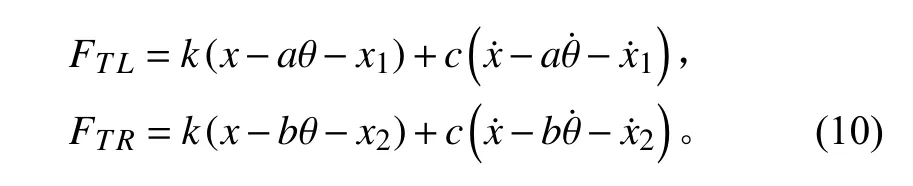
2.2.2 不平衡力矩作用下結構振動聲輻射特性

以設備產生的不平衡力矩為輸入載荷，分析計算結構的聲振特性。如果設備主要因為自身不平衡彎矩對外發出激勵，此設備以自身轉動為主。因此在分析設備不平衡力矩作用下，在設備質心處施加單位力矩，艙段結構在不平衡彎矩作用下振動聲輻射計算結果如圖7 所示。

可以看出，艙段結構在不平衡激振力矩載荷作用下，響應曲線趨勢與垂向力作用下曲線趨勢基本一致，在低頻處出現明顯振動峰值，但波峰數量以及峰值大小較不平衡力載荷作用時均有減小。在計算頻段內，艙段結構聲振特性曲線在大多數頻點相差5 dB 以內，且在垂向力作用下結構響應值較不平衡彎矩作用下響應值偏大，由此所計算出的結果可以認為是偏于安全的，所以對于以不平衡彎矩載荷為主的機械設備來說，將其等效為垂向力作用是可行的。隨著頻率的升高，振動頻譜特性更加豐富，小的振動峰出現頻率增大。部分典型振動峰值頻率下結構振型圖如圖8 所示。

由結構振動位移響應云圖可以發現，69 Hz 頻率時結構振型均表現為艙壁結構的1 階振動，119 Hz 處表現為甲板橫向2 階振動，側面艙壁主要表現為板格中心振動，隨著頻率的升高，結構主要表現為板格中心振動。

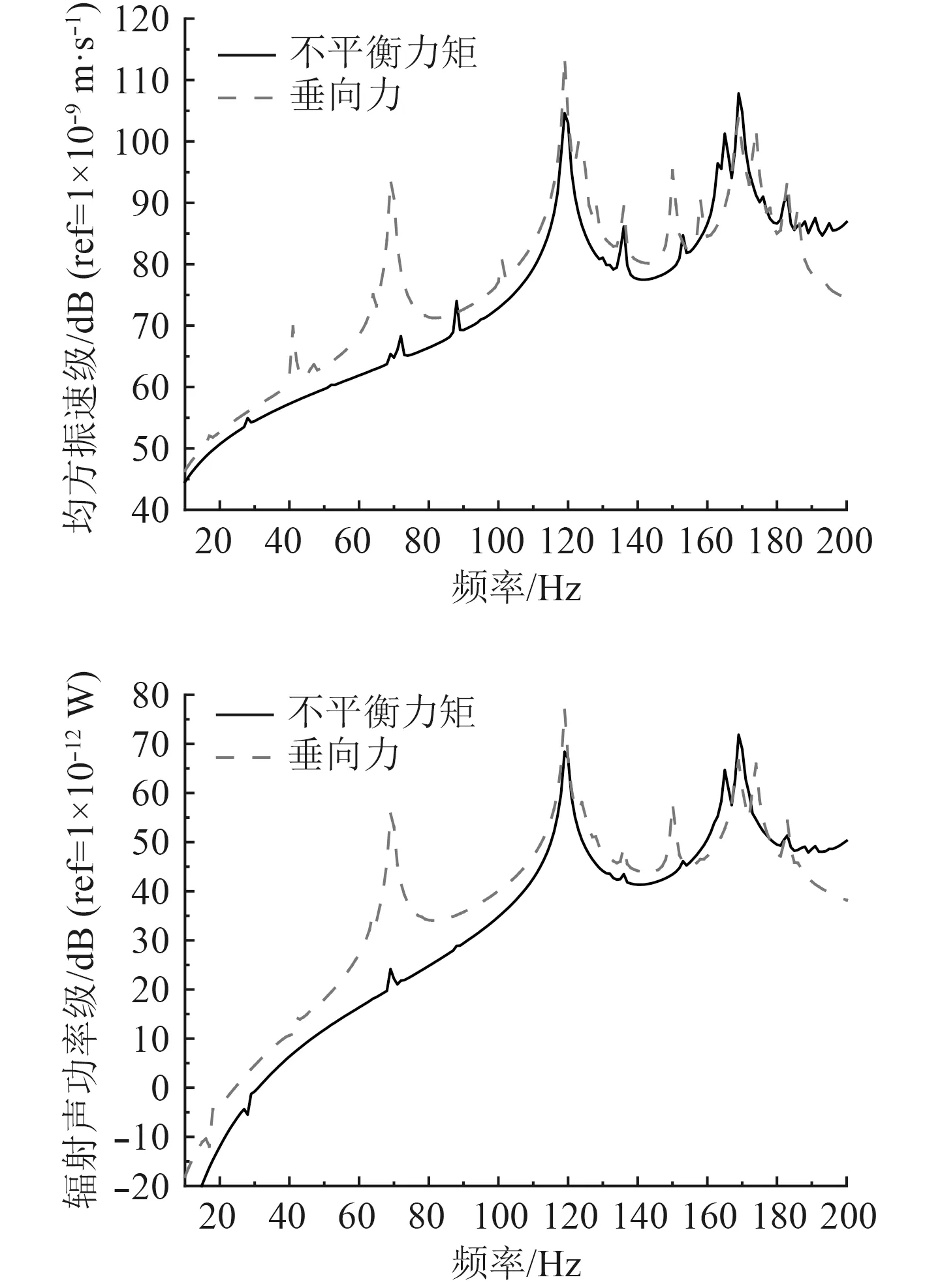
圖7 不平衡力矩作用下艙段結構振動聲輻射特性Fig.7 Vibration and sound radiation characteristics of cabin structure under unbalanced moment

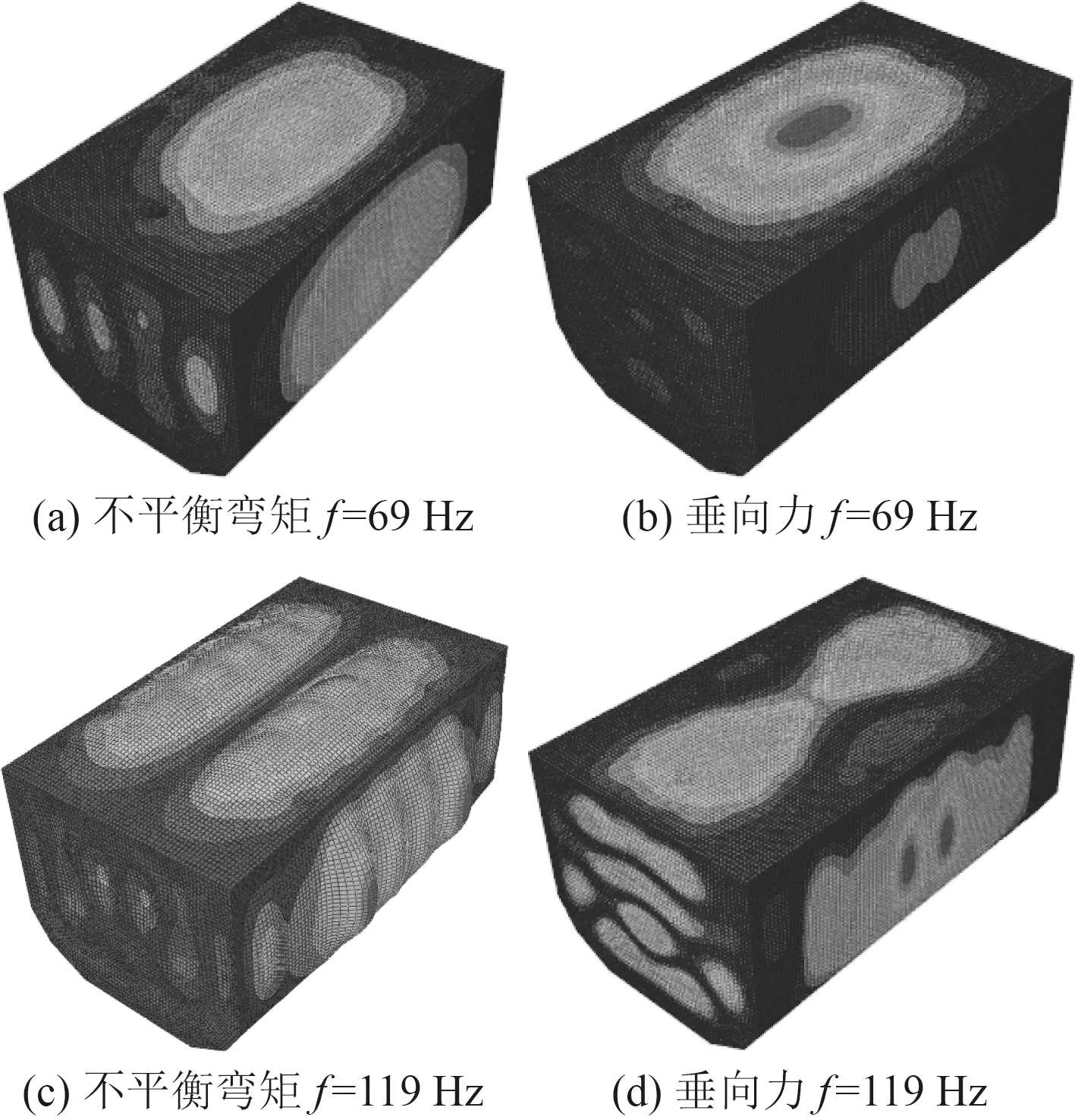
圖8 峰值頻點處振動位移響應云圖Fig.8 Vibration displacement response cloud diagram at peak frequency

2.3 設備不平衡力與力矩聯合激勵作用

2.3.1 設備對基座激勵力分析

當設備是不平衡激擾力和不平衡激擾力矩共同作用的情況時，該振動系統會同時出現上述所描述的激擾力方向的振動以及平面內的扭轉振動，仍按上述思路分析基座所受的載荷。

假設設備的不平衡激勵力和不平衡激擾彎矩的作用點為設備的質心，耦合系統分析模型進行簡化，如圖9 所示。

對設備基座聯立振動方程組，根據平衡條件，則設備通過隔振器向安裝基礎所傳遞的激勵力可表示為：

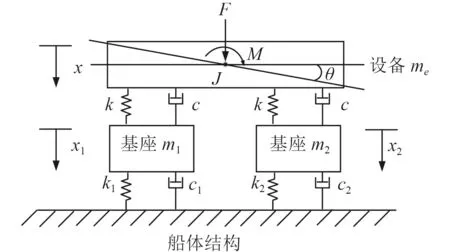
圖9 不平衡力與力矩聯合作用下設備與基座耦合模型圖Fig.9 Coupled model diagram of equipment and base under the combined action of unbalanced force and moment

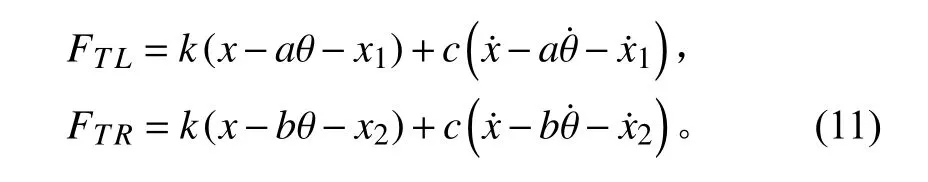
2.3.2 不平衡力與力矩聯合作用下結構振動聲輻射特性

當設備激勵既有不平衡力又有不平衡力矩時，在設備質心處施加不平衡單位力與不平衡單位力矩，艙段結構在不平衡力與不平衡力矩聯合作用下振動聲輻射計算結果如圖10 所示。

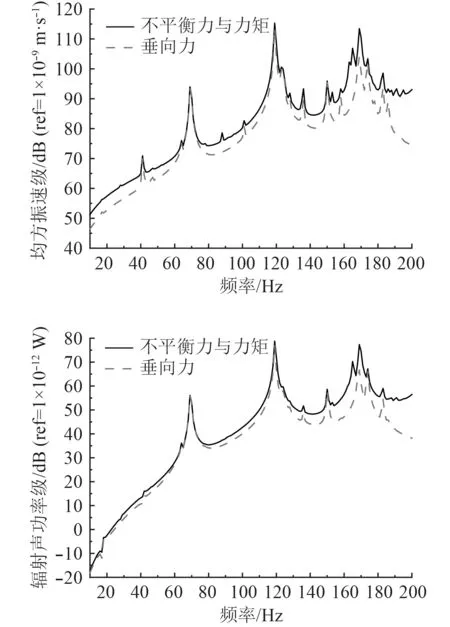
圖10 不平衡力與不平衡力矩聯合作用下艙段結構振動聲輻射特性Fig.10 Vibration and sound radiation characteristics of cabin structure under the combined action of unbalanced force and unbalanced moment

可以看出，艙段結構在不平衡激振力與激振力矩載荷聯合作用下，在低頻處出現明顯振動峰值，且峰值數量較不平衡力單獨作用或不平衡彎矩單獨作用時更為豐富，幅值也較載荷單獨作用時有一定增加；與垂向力單獨作用相比較，不平衡力與力矩聯合作用情況下結構響應略微增大，在大多數頻點響應值相差4 dB以內，但在艙段結構固有頻率所對應的頻點處，峰值大小相差較小，響應值相差小于1 dB，可見在不平衡力與力矩等效為垂向載荷作用時，仍能有效地反映出結構振動特性。隨著分析頻率的增大，振動頻譜特性更加豐富，小的振動峰出現頻率增大。部分典型振動峰值頻率下結構振型圖如圖11 所示。

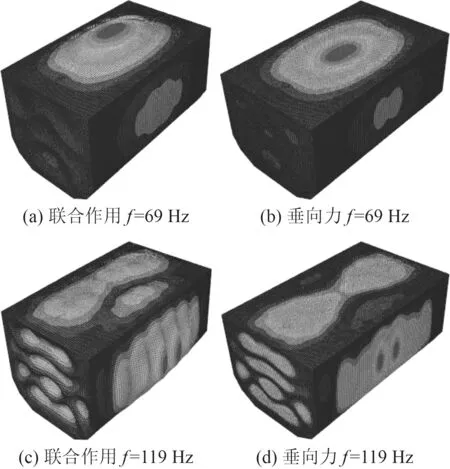
圖11 峰值頻點處振動位移響應云圖Fig.11 Vibration displacement response cloud diagram at peak frequency

由結構振動位移響應云圖可以發現，69 Hz 頻率時結構受迫振動振型均表現為甲板結構的1 階振動，119 Hz處表現為甲板2 階振動，側面艙壁主要為板格中心振動，隨著頻率升高，結構模態信息更為豐富，主要表現為板格中心振動。

3 結 語

本文首先對聲固耦合方法進行簡單闡述，在此基礎上，從“設備-基座-船舶結構”系統耦合振動角度出發，針對設備不平衡激擾力、不平衡激擾力矩、不平衡激擾力與力矩聯合作用等典型設備激勵載荷，以船舶結構振動與輻射噪聲為考核量，探究艙段結構在設備不同典型設備激勵載荷作用下輻射噪聲的影響變化，得出如下主要結論：

1）艙段結構在不平衡激振力載荷作用下相應曲線趨勢與垂向力作用下響應曲線趨勢基本一致，振動峰值所對應的頻率基本相同。對于以不平衡力載荷為主的機械設備來說，垂向載荷起到主導作用。隨著頻率的升高，振動頻譜特性更加豐富，小的振動峰出現頻率增大。

2）艙段結構在不平衡激振力矩載荷作用下，響應曲線趨勢與垂向力作用下曲線趨勢基本一致，在低頻處出現明顯振動峰值，但波峰數量以及峰值大小較不平衡力載荷作用時均有減小。對于以不平衡彎矩載荷為主的機械設備來說，將其等效為垂向力作用是可行的。隨著頻率的升高，振動頻譜特性更加豐富，小的振動峰出現頻率增大。

3）艙段結構在不平衡激振力與激振力矩載荷聯合作用下，在低頻處出現明顯振動峰值，且峰值數量較不平衡力單獨作用或不平衡彎矩單獨作用時更為豐富，幅值也較載荷單獨作用有一定增加。可見在不平衡力與力矩等效為垂向載荷作用時，仍能有效反映結構振動特性。隨著分析頻率的增大，振動頻譜特性更加豐富，小的振動峰出現頻率增大。