基于承運人視角的運輸線路組合問題及粒子群算法求解
郭俊
(重慶交通大學經濟與管理學院,重慶400074)
0 引言
物流組合問題是指將物流領域內的單一問題或單一因素綜合考慮,再設計適當的求解算法對組合問題求解。邱國慶等人[1]提出運輸任務分配與路徑選擇的組合優化問題,并針對該問題建立了組合優化模型,設計了基于二維染色體結構的改進遺傳求解算法。Mesa-Arango R 等人[2]在任務可搭載的基礎上,將m-PDVRP 模型應用在零擔物流車輛路徑優化中,并且采用分支定界算法對模型進行解。而其他研究者使用了諸如禁忌搜索法[3]、粒子群算法[4]等智能算法求解可搭載問題。
綜上所述,少有研究者關注運輸線路組合問題,雖多基于承運人視角,但更關注任務執行階段。因此,本文著重于任務選擇,并根據任務選擇情況規劃車輛路徑。
1 問題描述和建立模型
1.1 問題描述
本文研究問題如下:無向圖G=(V,E)為運輸網絡,其中 V={0,1,2,…n}表示所有運輸節點,0 表示車場。邊集合E={(i,j)|i,j∈V},每個邊上的單位成本為cij;∞1和∞2分別表示車輛空載和滿載情況下單位距離的油耗成本,則cij=(Qij,k/Q)(∞1-∞2),其中 Q、Qij,k分別表示車輛最大載重和邊(i,j)上的載重;各個節點的位置表示為(xi,yi),dij表示節點i,j 間的距離。假設某承運人的任務集合為C={1,2,3…n],任務t 的運價用pt表示,需求量用qt表示。在時間窗[elt,ltt]上增加了最大容忍上限eett和最大容忍下限eltt;承運人同型車輛集合 K={1,2,3…m],k 表示任意車輛,Lk表示車輛的最大行駛里程,v 表示速度。承運人在運力范圍內選擇f 個任務,當承運人選擇承運任務t 時,Yt=1,否則Yt=0。當車輛 k 經過邊(i,j),決策變量 Xij,k=1;否則,Xij,k=0。當任務 t 分配給車輛 k,決策變量 Zt,k=1;否則,Zt,k=0。
1.2 建立模型
基于上述分析和變量的設置,建立以承運人收益最大化為目標的數學模型:

目標函數(1)表示承運人收益最大化;式(2)表示承運人的運力限制;式(3)表示物流流量的平衡;式(4)表示車輛的最大里程限制;式(5)表示車輛最大運量限制;式(6)~式(8)表示決策變量取值范圍。
2 算法設計
眾所周知,任務組合問題是NP-hard 問題,而對該類問題的求解是較為困難的。因此本文采用標準的PSO 算法[5]構架對模型求解。
2.1 粒子群算法
粒子群算法也稱粒子群優化算法,是由J. Kennedy 和R. C. Eberhart 等開發的一種進化算法。算法通過改變粒子的速度來控制粒子的飛行方向和距離,不斷產生由優化的函數決定的適應值,具體公式如下:

上式中,vi表示粒子 i 的速度,w 表示慣性權重;c1、c2表示兩個為常量的學習因子;pbesti和gbest 分別表示粒子群體中個體局部最優和全局最優位置;r1、r2為兩個0、1 之間的隨機數。
2.2 任務選擇
Step1:初始化,生成 n×N 隨機數矩陣,n、N 分別表示任務個數和粒子個數。
Step2:將隨機數進行四舍五入處理,0 代表不選擇,1代表選擇。
2.3 路徑規劃
Step1:計算單獨運輸任務t 的開始服務時刻Tt。
Step2:計算每個任務的初始時間執行權重φt,若Tt<eett,則 φt=0;若 Tt>eltt,則 φt=1;若 eett≤Tt≤eltt,則 φt=Tteett/eltt-eett。
Step3:將執行權重降序排列,確定首個任務點。
Step4:判斷是否為多任務起點,若是,則在不拆分的情況下盡可能多的裝載任務。
Step5:判斷車輛剩余運力,若運力不足,則完成已裝載任務的運輸后進入step6;若運量充足,則進入下一步。
Step6:更新執行權重,尋找下一節點。
Step7:判斷節點性質,若是pickup 點則返回step4;若是delivery 點,則卸載對應的任務。
Step8:判斷任務是否運輸完成,若完成進入下一步;若未完成則返回step6。
Step9:根據車輛行駛里程約束,拆分線路。
Step10:結束。
3 算例分析
該章節根據上述算法思想設計了數值算例,物流網絡節點距離信息和托運人任務信息分別如表1 和表2 所示。

表1 節點間距離表
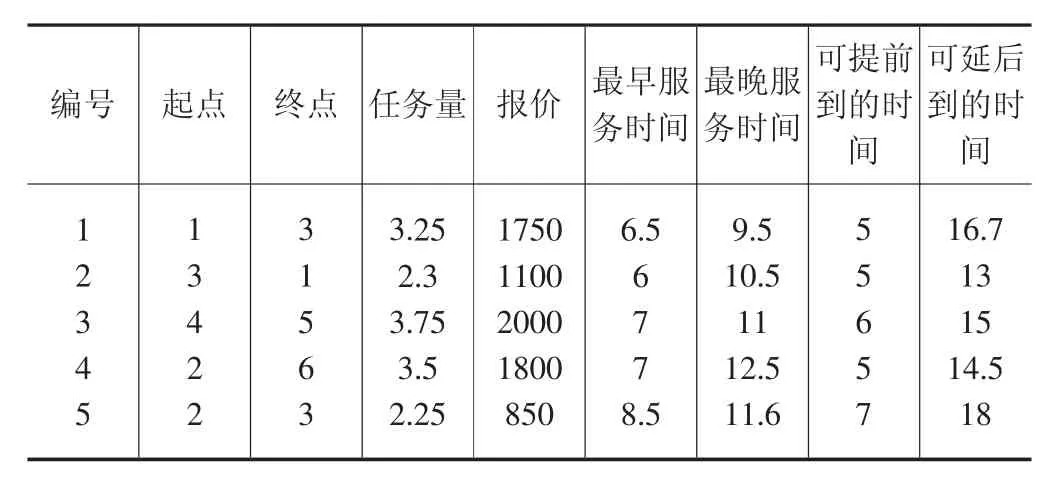
表2 任務信息表

表3 車輛信息表
粒子群參數設置為:種群規模為20,迭代次數為100,學習因子 c1=1.5,c2=0.3,ωmax= 0.4,通過 PSO 計算結果如圖1。

圖1 收益迭代圖
根據算法計算結果,承運人選擇承運任務1、2、3 和任務4 時,收益最大為4609.5 元。在設定承運人最大運力為13t 的情況下,算法選擇承運的總任務量為12.8t。而為了在車輛的行駛里程內完成任務的運輸,最少需要2 輛車。具體的車輛運輸信息表如表4 所示。

表4 車輛運輸信息表
4 結論
本文從承運人的視角對運輸線路組合問題展開研究,建立了承運人收益最大的數學模型。結果顯示,在承運能力允許范圍內,承運任務1、2、3 和4,承運人收益最大。因此,本文所以提出的算法對求解運輸線路組合問題具有一定的理論和應用價值,有利于承運人充分運用其運輸能力,避免造成資源閑置。同時,本文還存在些許不足之處。本文所研究的問題,是在運量不允許的拆分的情況下進行的。然而,就實際情況來看,適當的將需求進行拆分是可以降低承運人的運輸成本,達到增加承運人收益的效果。

