雙站測向陣列中點的目標到達角近似求解

郁 濤

(上海裕韜智能科技有限公司,上海201802)

0 引言

已有的研究結果表明,如果將程差方程和幾何輔助關系結合起來,就能得到平面雙基三站定位方程的線性解,由此即可得到適用于長基線的雙基三站程差測向公式。在此基礎上,通過適當的簡化處理,即可獲得長短基線都適用的單基中點測向解[1]。為進一步提高單基中點測向解的準確度,文獻[1]采用將程差的幾何投影式展開,并將站點處的到達角轉換為基線中點的到達角的方法,給出了一個基線中點目標到達角的嚴格解。這個嚴格解以站點處的到達角與增量角之和來表示單基中點方位角,但實際上其中的增量角是未知的。這個嚴格解最終僅在近似簡化消去增量角之后,給出了一個利用雙站交會角使計算準確度更高的近似解。

現有的單基中點測向解的解析分析是建立在程差測量的基礎之上的,和這種程差測量直接對應,基于雙站時差測量的高精度長基線測向或定位問題[2-3]已經被研究。雙站無源定位仍是一個極具發展潛力的研究課題[4]。作為整個拓展應用研究過程的一個過渡階段,本文從定位三角形的邊角關系入手,通過程差與角度之間的轉換,研究了基于雙站角度測量的陣列中點方位角的計算問題。主要目的是期望得到一個既簡單,又有較高計算準確度的解析計算式,以利于進一步的研究分析。

1 定位三角形的邊角關系

圖1為單基定位三角形的示意圖。其中,T為被探測目標,S1和S2表示探測站點,d為站點間基線長度,r1和r2分別為對應站點的目標徑向距離,α1和α2分別為兩站點處以站間基線為測量基準的目標方位角。

根據圖1中定位關系,由正弦定理可得到

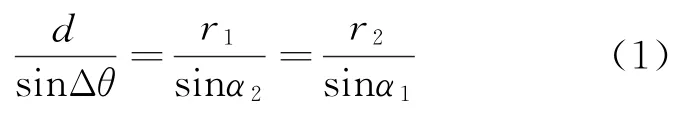
式中:Δθ=180°-α1-α2為目標處的交會角。

由式(1)可得到兩站點到目標的徑向距離

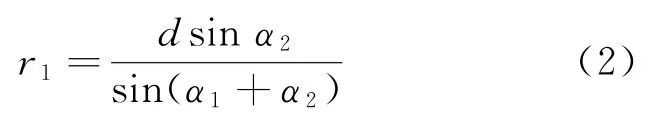
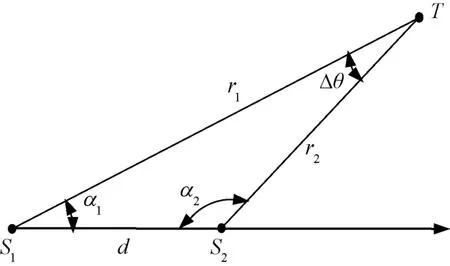
圖1 單基定位三角形

如將兩徑向距離相減,則可得到站點S1和站點S2間的程差Δr1]2與方位角之間的關系式

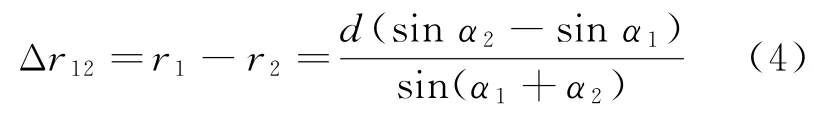
圖2為一維雙基定位三角形的示意圖。站點S2位于站點S1、站點S3連線中點,d為站點S2與站點S1、站點S3]間基線長度,r1、r2、r3]分別為對應站點的目標徑向距離,α1、α2、α3]分別為對應站點處以站間基線為測量基準的方位角,θ2為站點S2的目標到達角。可以分別得到相鄰兩個站點間程差和方位角的關系式。其中,Δ r1]2與方位角關系見式(4),Δ r2]3與方位角關系式為

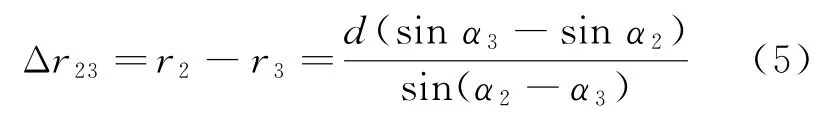
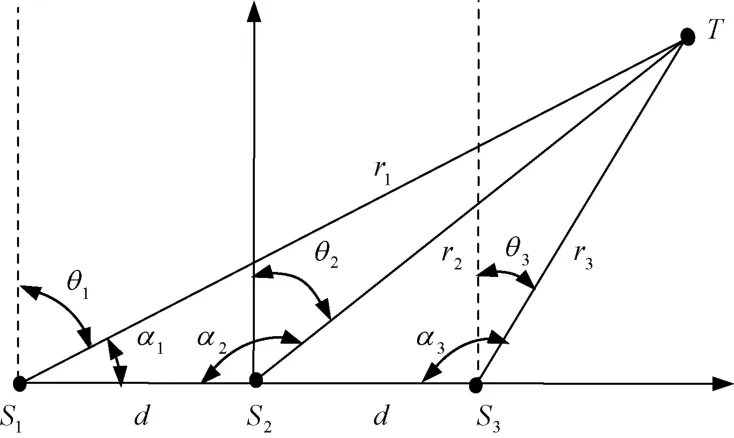
圖2 一維雙基定位三角形

對于整個雙基定位三角形,利用上述的方法,可得到站點S1和站點S3間程差Δ r1]3和方位角之間的關系式

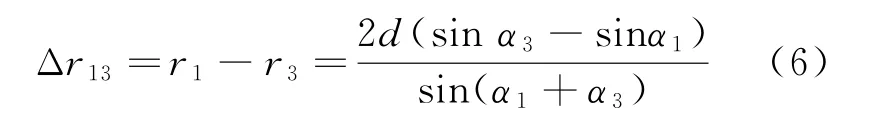
2 從程差到角度的變換

2.1 基于程差測量的近似測向公式

通過直接對一維雙基測向公式[1]中程差的高階項做近似處理,可得到僅與程差測量相關的目標到達角θ2的單基近似測向解[2]

借助幾何投影的方法,將基線投影到程差所在的徑向方向上,可得到一個能利用雙站間的交會角有效提高計算準確性的單基修正近似測向解

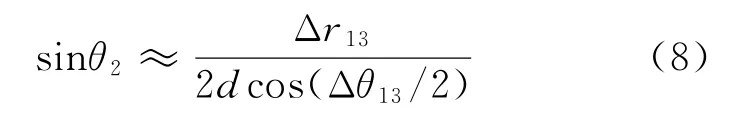
式中:Δθ1]3=180°-α1-α3,是站點S1和站點S3之間的交會角。

2.2 近似的幾何解釋

如圖3所示,對于雙站定位系統,由目標和兩個觀測站所構成的定位三角形△S1TS2可被分解為兩個三角形:一個是和程差相關的,稱之為程差三角形△S1BS2;另一個是扣減程差三角形后所得到的等腰三角形△BTS2。

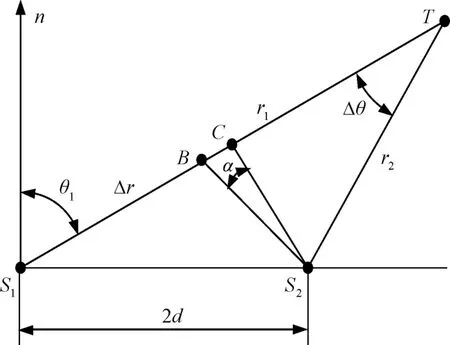
圖3 定位三角形的分解

對于等腰三角形△BTS2,根據兩底角相等的條件,可得

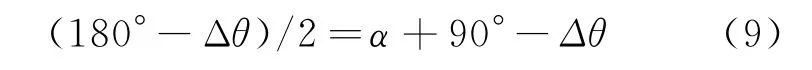
式中:α=∠BS2C為修正角。

由此即可證得

根據圖3所示的幾何關系可得

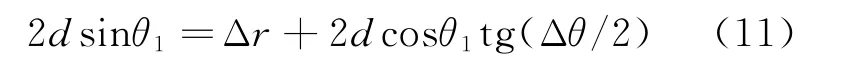
如忽略實測程差所在直角邊的修正長度Δa=2dcosθ1tg(Δθ/2),則即得到近似測向解。

2.3 邊角關系的演繹

將式(6)代入式(7),可直接給出利用陣列兩端點測向值的單基中點測向解

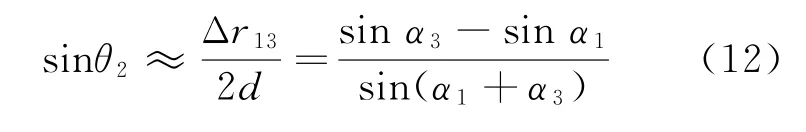
利用三角函數的倍角關系以及和差化積關系,可將式(12)變形為

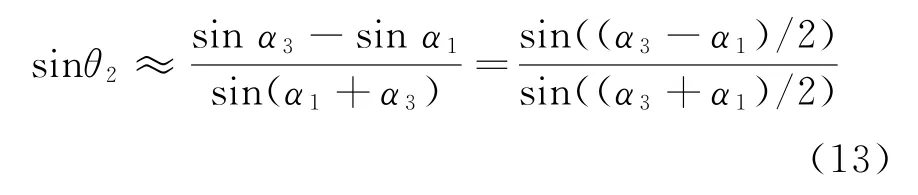
從圖2可知方位角與到達角之間的關系為α1=90°-θ1和α3=90°+θ3,代入式(13),有

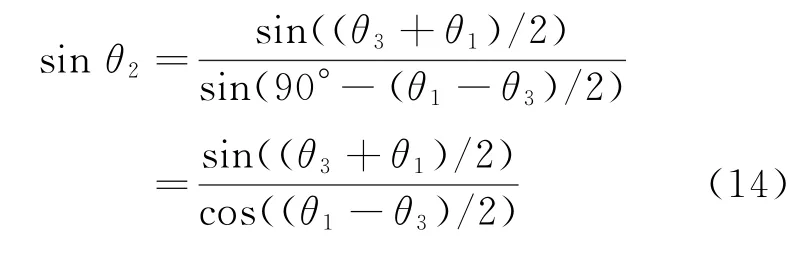
對于遠距目標,θ1-θ3將是一個很小的量,此時cos((θ1-θ3)/2)近似為1,于是近似有到達角之間的中值關系為

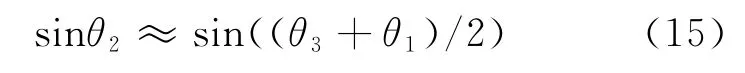
因此,在雙站陣列中點的目標到達角可以直接用陣列端點處的到達角進行近似估計。

3 基于程差關系的雙站測算解

對于圖2所示一維雙基陣列,程差之間關系式為

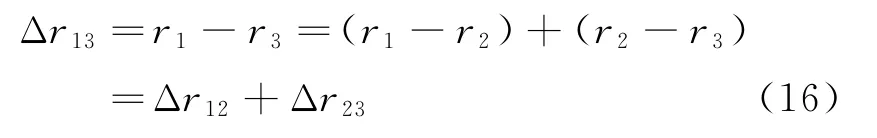
根據式(4)～式(6),將基于角度測量的程差表達式代入式(16),得到

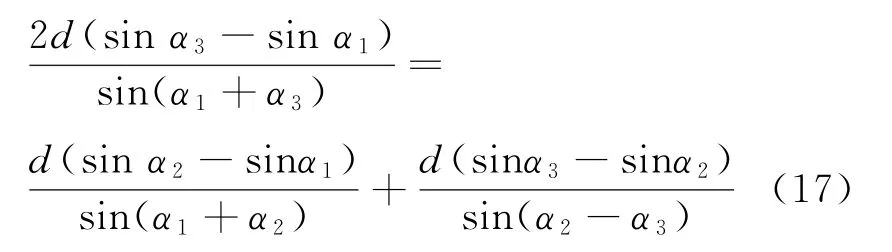
將陣列中點的方位角α2作為未知量求解,且為形式簡單,上述方程的左端直接用Δ r1]3表示。可解得方程

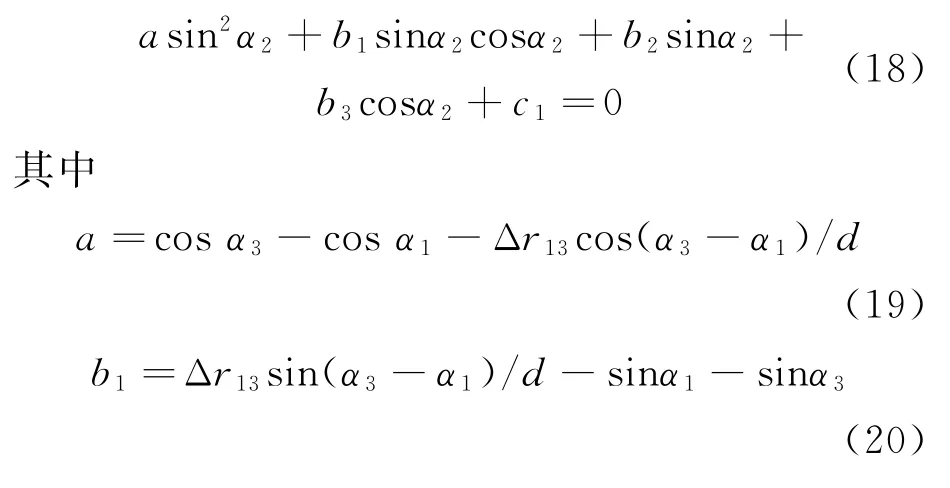
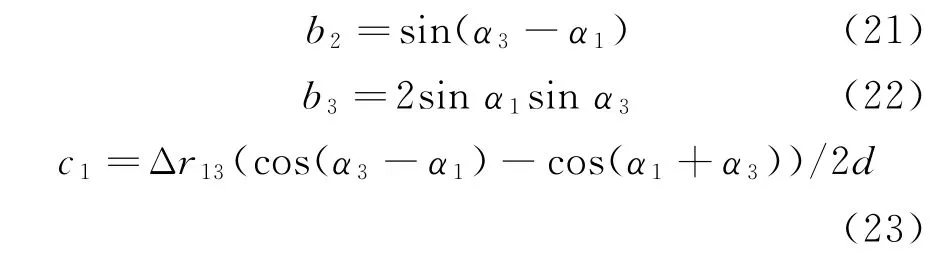
在此基礎上,如進一步做函數變換,例如將余弦函數化為正弦函數,則將出現一元四次方程,即使給出顯示解亦難以應用于工程解析分析。為此采用近似,先將式(18)中的余弦函數變換為

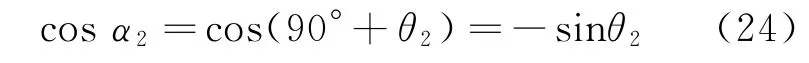
將式(8)代入式(24),得到

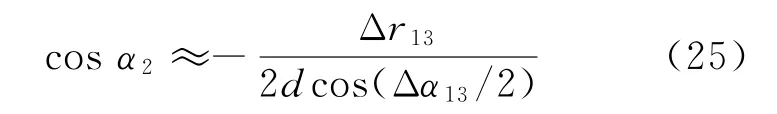
于是,求解方程式(12),可表示為

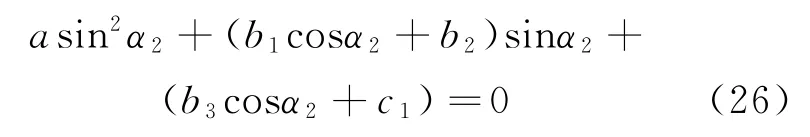
進一步的簡潔表示為

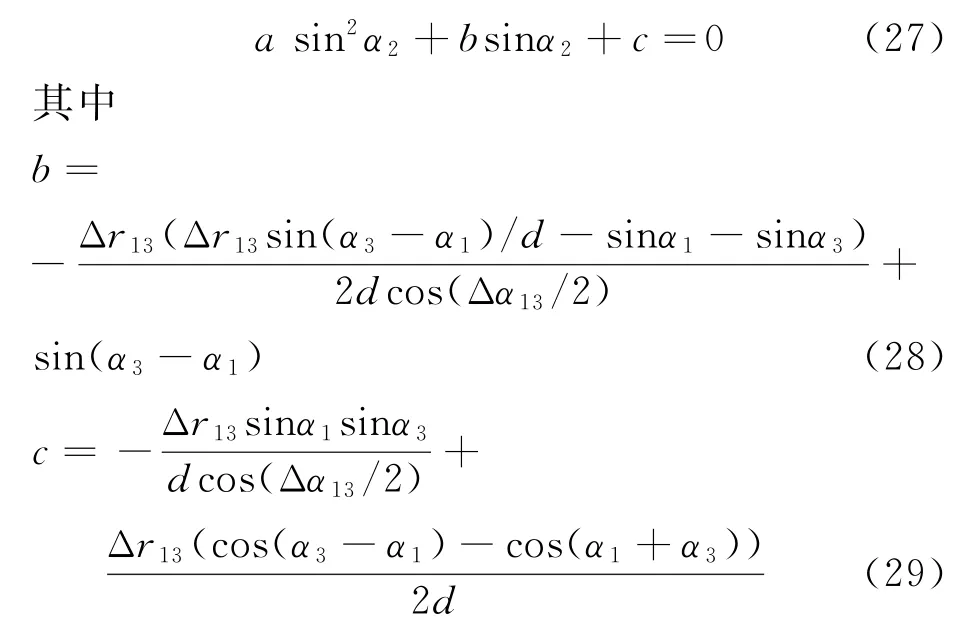
經計算驗證,基于程差關系的雙站測算解公式為

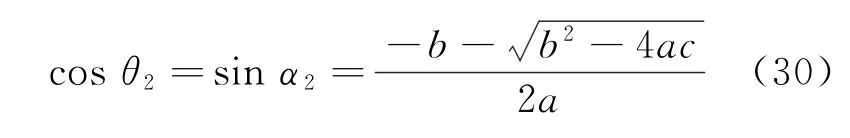
4 計算準確度分析

4.1 相對計算誤差理論參考值

從理論角度,為確定計算準確度,可使用文獻[1]給出的雙基測向解作為基于雙站測向角測算陣列中點目標到達角的理論參考值。計算公式為

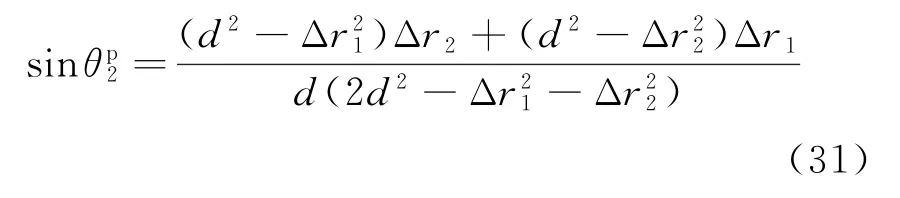
式中:上標p表示是理論值。相對計算誤差為

但實際模擬計算時,為處理簡單,是先直接設置中點到達角、中點徑向距離和基線長度,并讓預設的陣列中點到達角在指定區間內線性變化,然后用預設值計算出定位三角形內的各個幾何參量,由此就可按式(30)給出陣列中點目標到達角的計算值。

圖4給出了當目標距離為300km時,不同基線長度情況下的相對計算誤差理論值。計算結果表明,對于300km遠的目標距離,只要站間距離小于200km,則基于雙站測向角測算陣列中點目標到達角的相對計算誤差就能小于1.5%。如果站間距離大于200km,則雙站測算解將不再有效。

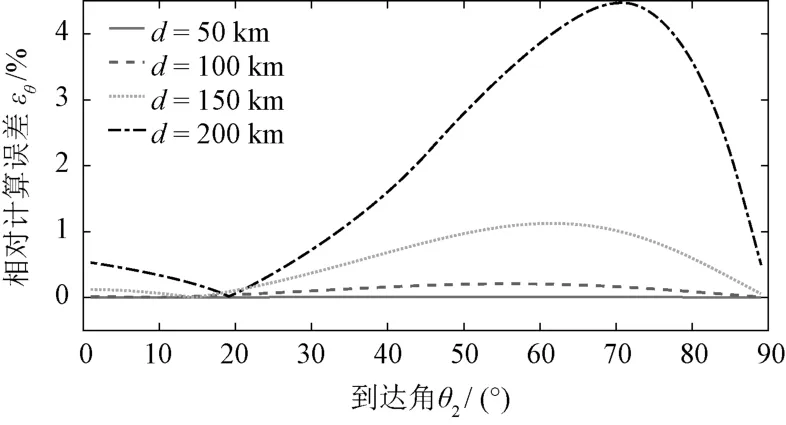
圖4 不同基線長度的相對計算誤差

4.2 解算準確度比較

圖5給出了雙站測算解和修正近似解的相對計算誤差。計算的參數為:基線長度d=100 km,目標距離r2=300km。由圖示曲線可見,雙站測算解的計算準確度略高于修正近似解。

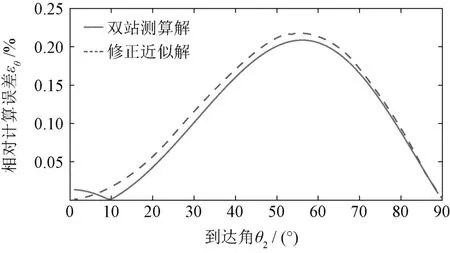
圖5 計算準確度的比較

5 結束語

基于角度測量的數學處理過程較為繁雜。基于雙站角度測量,利用相鄰兩基線的程差和關系,所得到的單基中點測向的嚴格解析解涉及一元四次方程,直接求解高階方程所得到的嚴格解析解并不適合工程解析分析。本文的分析僅是初步確定,利用雙站交會角改進單基中點修正近似測向解的計算準確度和雙站測算解的計算準確度基本相同,換句話說就是用修正近似解即可取代高階近似的解析解。