導引頭電子艙框架有限元仿真及模態試驗

陸 玥, 劉亞龍, 劉 宇, 張發洋

(上海無線電設備研究所,上海201109)

0 引言

導引頭電子艙在導彈飛行過程中,會受到發動機及氣動力矩的受迫振動、各種沖擊、過載效應和噪聲干擾的綜合作用,始終處于復雜激勵狀態。隨著導引頭朝向小型化、輕量化的方向發展[1],要求結構件更加輕薄。隨之帶來電子艙結構強度下降,振動量級過大等問題,可能會導致產品工作異常。同時,隨著相控陣技術的應用和復合體制導引頭的普及,導引頭結構發生了較大改變。傳統的經驗設計參考價值不高,需要對新體制的導引頭進行細致的力學分析,保證結構設計的可靠性[2]。

模態特征能夠從質量和剛度特性上反映結構的力學性能。采用仿真或試驗的方法對產品進行模態分析,可以清楚了解結構在某一易受影響頻率范圍內的各階主要模態特性,為結構系統的振動特性分析、振動故障診斷以及結構動力特性的優化設計提供依據。其中有限元模態仿真分析靈活便捷,可以快速得出模態振型,用以指導模態試驗力錘激勵點位置排布。但是仿真結果依賴仿真工程師經驗,難以一次性保證仿真置信度。試驗模態分析可以直觀地顯示結構的動力學特性,得到的低階模態固有頻率和模態振型結果非常可靠。但是模態試驗對試驗條件有一定要求,大型結構的模態試驗時間較長。對復雜結構進行模態試驗[3-4]是結構動力學設計中必要的環節。同時,使用模態試驗得到的參數對有限元仿真模型進行修正,是建立足夠精確的有限元模型的重要手段[5-7]。本文對某導引頭電子艙框架結構進行有限元模態仿真分析及模態試驗,分別得到電子艙框架的固有頻率和振型,并進行比較,驗證仿真分析的可靠性。

1 模態分析原理

模態分析的主要目的是分析系統的固有特性,從而確定模型的固有頻率和相應振型。假定在無激勵無阻尼的作用下,模型的振動方程為

式中:M為質量矩陣;K為剛度矩陣;為節點速度矩陣;u為節點位移矩陣。可將模型變為簡諧運動,令ω為角頻率,u=u(t)ejω t。求解可以得到ω的多個解,任意一個解代入u可以得到相應位移變化矩陣,進而得到模型固有振型。

真實情況下模型會有阻尼,并且存在外部激勵。此時的線性微分方程為

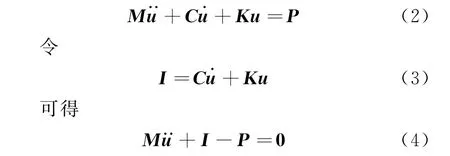
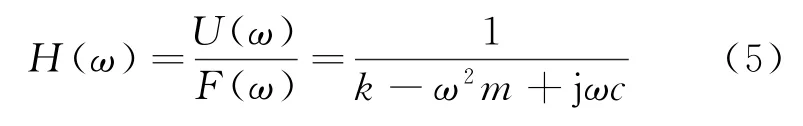
式中:m、k和c分別表示系統的質量、剛度與阻尼。而對于n輸入和n輸出的線性時不變多自由度系統(n≥2),它的頻率響應函數為一常數矩陣,表示為

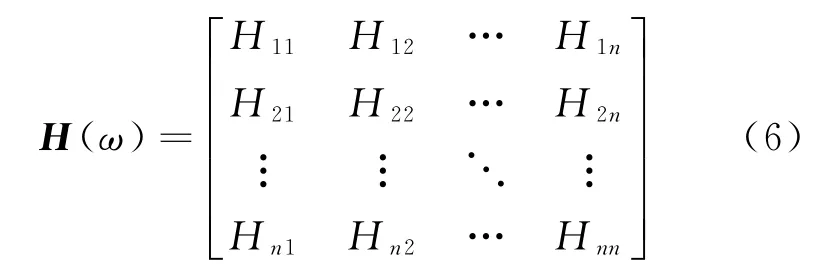
式(6)中的任一元素Hl p的表達式為

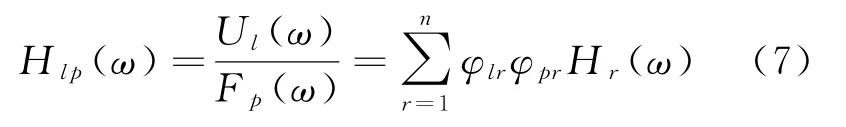
式中:l為響應點自由度;p為激勵作用點自由度;φ表示振型函數;Hl p表示在p自由度上作用單位力時,在l自由度上所引起的響應,即l和p兩點之間的頻響函數。

2 電子艙框架結構模態仿真

2.1 仿真模型的建立及網格劃分

將在Pro/E三維軟件中建立的導引頭電子艙框架幾何模型導入到網格劃分軟件Hyper Mesh中進行有限元仿真分析。在分析過程中,需要對模型進行適當的簡化處理。由于在仿真中沒有使用到的螺紋孔對模態影響極小,同時較小的孔處理不當可能會導致網格畸形,影響計算結果,因此對其進行幾何清理。本文采用Hyper Mesh四面體網格劃分功能,對螺紋孔等特征較為密集的地方進行細化處理,其他部分網格較為稀疏。劃分結果如圖1所示。該處理方法可以極大地提高計算效率,同時也可以保證計算精度。

圖1 導引頭電子艙框架有限元網格劃分

2.2 材料屬性設置

電子艙框架包含連接環、梁、底板及緊固件。其中連接環、梁和底板材料為鋁合金(2A14),螺栓為不銹鋼(1Cr18Ni9Ti)。各材料屬性見表1。

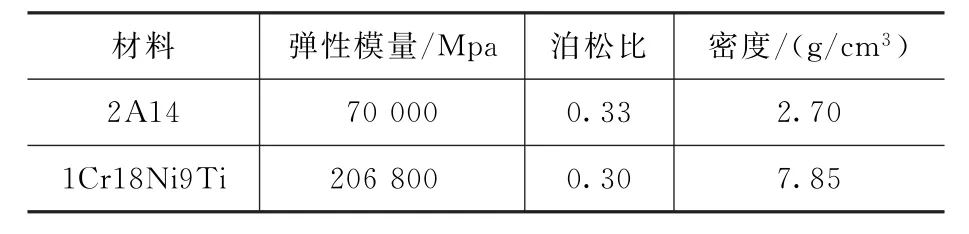
表1 模型材料屬性

2.3 螺栓連接等效方法

結構件之間經常使用螺栓進行連接和固定,各結構件連接處的處理方式對有限元仿真精度的影響極大[8]。如果根據實際結構建立仿真模型,會使模型邊緣復雜、結構自由度增加,導致網格劃分困難、計算時間增加,甚至產生仿真結果不收斂問題,導致仿真計算失敗[9]。在結構分析中,很多時候只需考慮結構整體性能,通過對模型和連接方式進行簡化處理,將復雜的結構形式進行等效,便于網格的優化,加快計算速度。

Hyper Mesh中提供了強大的一維單元創建功能,可以簡化并等效螺栓連接、焊接和粘接等常用的連接方式,用戶可以根據自己的模擬需要選擇不同的一維單元。本文使用梁截面工具Hyper Beam創建剛性(rbe2)單元。rbe2單元是一種模擬多節點自由度耦合關系的單元,可以用來模擬剛度非常大的構件,如螺栓與結構件的螺紋連接。如圖2所示,rbe2單元將螺紋孔中的網格節點進行剛性抓取,將螺紋孔的剛度集中在一點上,以代替兩端的螺紋連接。桿(bar)柔性單元可以用來模擬螺栓的螺桿等一個方向尺寸遠大于另外兩個方向的構件。如圖3所示,使用bar單元分別連接兩個rbe2單元的集中點,同時定義bar單元的橫截面積和材料參數。由此bar單元和rbe2單元就可以組合成為一種簡化螺栓的連接方式。螺栓連接的整體等效方式如圖4所示。

圖2 rbe2單元等效螺栓的螺紋

圖3 bar單元連接方式

2.4 模態仿真結果

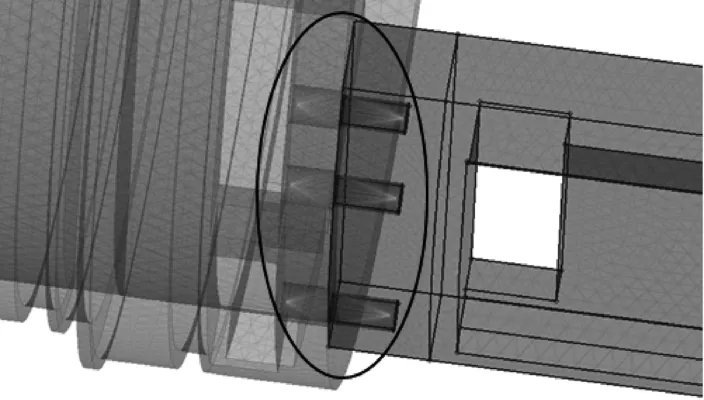
圖4 螺栓連接等效方式

利用Nastran軟件分析上述模型的自由振動模態,即自由狀態下結構振動特性,得到400Hz以內的固有頻率依次為120.1,173.6,249.3,339.8Hz,對應振型如圖5所示。其中1階為整體橫向的同側彎曲變形,2階為整體縱向的異側彎曲變形,3階為梁橫向的異側彎曲變形,4階為梁橫向的同側彎曲變形。

圖5 仿真振型

3 電子艙框架結構模態試驗

模態試驗可以從實際結構的激勵和響應數據中辨識結構的數學模型和特性參數。工程應用中,可以用模態試驗的結果驗證和修正仿真模型,校核動態分析結果的有效性,檢查結構中的薄弱點及鑒定結構的動態特性是否符合設計要求。

3.1 試驗方案

模態試驗采用的主要設備有東華DH 5902信號采集處理系統、安裝江蘇東華模態分析軟件的計算機、B&K公司三軸向加速度傳感器、力錘。

進行模態試驗前,需要在模態分析軟件中建立試驗模型。通過仿真得到的振型確定節點位置,并在電子艙框架結構上標出與試驗模型節點對應的激勵點,作為力錘敲擊的位置。本次試驗采用跑錘法進行激勵,即使用力錘敲擊不同激勵點,傳感器位置不改變,采集各點的頻響函數進行模態識別。試驗模型如圖6所示。

圖6 試驗模型

模態試驗分析關鍵步驟包括施加激勵、參數采集、參數識別等。為了獲得所關注頻率范圍內的所有模態振型,應該合理地選擇激勵點與響應點,并完成相關參數的設置。為了更好地模擬導引頭電子艙框架的工作環境,排除外界物體振動對框架的干擾與影響,本試驗采用彈性細繩懸掛的方式來模擬自由邊界條件。

測試系統框圖如圖7所示。將電子艙框架懸吊好后,貼好加速度傳感器,打開信號采集處理系統,設置好相應參數。使用力錘敲擊框架上標記好的激勵點,為保證精確度,每個點敲擊四次進行平均。待所有點都敲擊完成后,使用模態分析軟件對采集到的數據進行處理,即可得到模態頻率及其對應的振型。

圖7 試驗測試系統框圖

3.2 試驗結果及對比分析

通過對試驗數據進行分析、處理,識別模態參數,得到400Hz以內的試驗振型如圖8所示。模態試驗得到的被測件固有頻率依次為125.6,177.5,230.1,325.1Hz,各頻率對應的振型與有限元仿真結果一致。

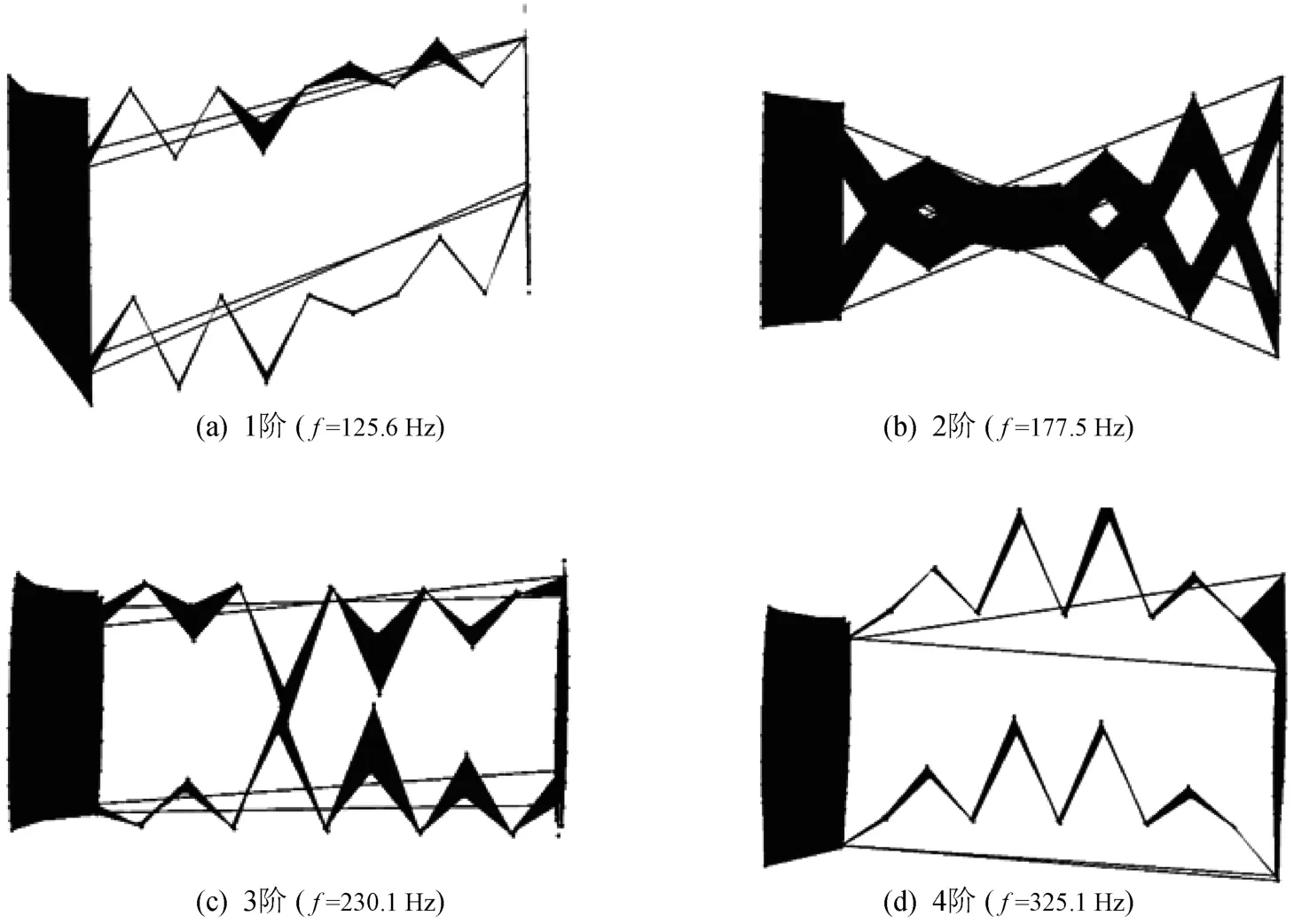
圖8 試驗振型

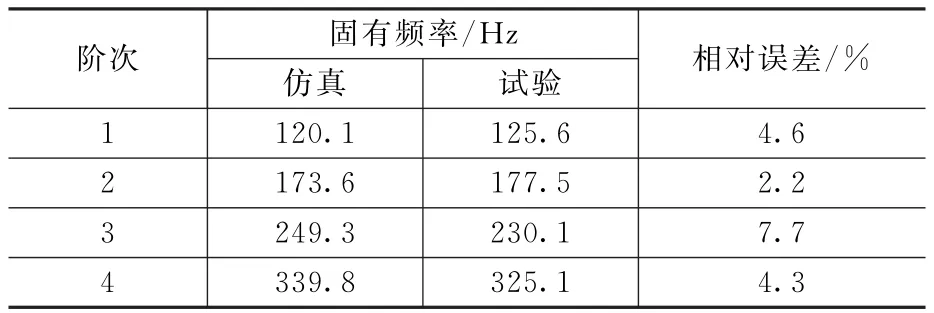
表2 有限元仿真與試驗獲得的固有頻率對比

綜合對比試驗結果和有限元仿真結果,二者所得固有頻率對比如表2所示,仿真與試驗所得固有頻率在數值上最大相對誤差為7.7%。經分析初步判定,二者不一致的主要原因包括:a)試驗中被測件螺栓連接處結構較為復雜,與有限元中簡化的結構相比,質量更大;b)試驗中通過細繩懸掛框架來模擬自由邊界條件,繩子具有一定剛度,不能完美復現有限元仿真中的自由狀態;c)傳感器等增加了試驗中被測件的質量;d)力錘激勵、采集電纜以及人為操作導致試驗結果存在誤差。但是通過對比振型可以看出,試驗所得振型與有限元仿真中所得振型完全符合,因此仿真結果較為準確。

4 結論

本文建立了導引頭電子艙框架結構模型,并提出了一種螺栓等效方法,進行了有限元模態仿真,得到其400Hz以內固有頻率及模態振型。通過力錘激勵方法對該結構進行了模態試驗,并與仿真結果進行對比,試驗測得的固有頻率與仿真結果相對誤差均在10%以內,并且模態振型完全一致,驗證了仿真結果的準確性。在后續結構設計中,可用該仿真方法進行結構強度與剛度校核。