基于可靠度理論的水下大直徑盾構隧道耐久性設計

武建力 高 抗

(中交第二公路勘察設計研究院有限公司 武漢 430056)

隨著國內(nèi)盾構技術的成熟，大直徑盾構法在水下隧道工程中得到了廣泛應用。武漢三陽路長江隧道、上海長江隧道、杭州錢江隧道等超大直徑盾構隧道越來越多。盾構隧道管片的結構耐久性問題關系到隧道使用壽命、舒適度等多方面，結構使用環(huán)境能明顯地導致結構材料性能隨使用時間的延長而劣化，因此水下大直徑盾構隧道管片耐久性設計是結構設計必不可少的重要內(nèi)容。

管片襯砌結構在投入使用后，受到混凝土碳化、氯離子侵蝕等各種環(huán)境因素的作用，最終會引起鋼筋銹蝕，混凝土截面損傷，以及鋼筋與混凝土之間的黏結性能退化，從而導致隧道襯砌結構承載能力逐步降低，結構失效。因此，在襯砌結構耐久性損傷過程中，環(huán)境因素起了決定性的作用，而地下復雜環(huán)境也給混凝土的耐久性帶來了極大的挑戰(zhàn)[1]。

隧道襯砌結構耐久性是與時間相關的，是由襯砌結構外界環(huán)境和本身因素共同作用下所達到的使工程結構正常使用的年限[2]。水下隧道襯砌主體結構設計使用年限一般為100年，有的隧道甚至提出更高的年為(港珠澳大橋設計使用年限為120年)。因此，為了保證水下大直徑盾構隧道100年的設計使用年限，有必要對隧道襯砌結構耐久性設計進行研究，不僅具有重大的經(jīng)濟意義，也可為今后類似水下盾構隧道耐久性設計提供理論依據(jù)。

1 大直徑盾構隧道結構耐久性設計

李田、劉西拉提出的基于近似概率的耐久性設計方法，從計算和構造要求兩部分進行耐久性設計[3-4]。在計算和驗算過程中，采用現(xiàn)行結構設計規(guī)范GB 50010-2010(2015版)《混凝土結構設計規(guī)范》中極限設計表達式中加入耐久性設計系數(shù)的方法，與該規(guī)范相協(xié)調(diào)。該方法概念明確，形式簡單，而且易被工程設計人員熟悉和掌握。同時，考慮了抗力隨時間衰減的變化規(guī)律，使新建結構有明確的目標使用年限，達到結構安全、經(jīng)濟、耐久和實用的建設目的。基于此，本文建立的水下大直徑盾構隧道襯砌結構耐久性設計方法就是基于近似概率法的耐久性設計方法，同時結合DuraCrete方法，將參數(shù)考慮為隨機變量。

1.1 基于近似概率法的耐久性設計方法

現(xiàn)行的GB 50010-2010(2015版)混凝土結構設計規(guī)范中關于計算與驗算部分的公式可以歸納為式(1)所示形式。

S≤R

(1)

式中：S為結構內(nèi)力(作用效應)設計值；R為結構抗力設計值。

基于式(1)，可得混凝土結構耐久性設計的極限狀態(tài)功能函數(shù)隨機過程表達式如式(2)。

Z(t)=R(t)-S(t)

(2)

式中：Z(t)為混凝土結構極限狀態(tài)功能函數(shù)隨機過程；R(t)為混凝土結構抗力衰減隨機過程；S(t)為混凝土結構荷載效應隨機過程。

結構構件在內(nèi)外因素的共同作用下，隨著時間的增長會發(fā)生耐久性損傷，結構承載力下降，即結構抗力R(t)是隨時間增長而降低的隨機過程；而荷載效應S(t)在使用期內(nèi)可能會發(fā)生變化，但由于構件受力方式、構件結構形式和荷載作用形式基本恒定，所以在正常情況下變化的幅度很小。因此，在考慮耐久性損傷的情況下，引入結構安全系數(shù)和耐久性設計系數(shù)，則基于近似概率的耐久性設計極限狀態(tài)方程見式(3)。

r0S(t)≤ηR(t)

(3)

式中：r0為結構安全系數(shù)；η為耐久性設計系數(shù)，是可靠度指標的函數(shù)，可表示為

(4)

式中：β為規(guī)范[5]中規(guī)定的可靠度指標；βt為達到使用年限時的可靠度指標，一般取βt=β0；β(t)為結構使用期限內(nèi)可靠度指標下降的過程，是時間t的函數(shù)。

綜上所述，進行結構耐久性設計主要是求得結構抗力R(t)衰減的隨機過程、結構荷載效應S(t)的隨機過程，及可靠度指標β(t)。

1.2 大直徑盾構隧道襯砌結構耐久性設計流程

大直徑盾構隧道襯砌結構耐久性設計流程圖見圖1。

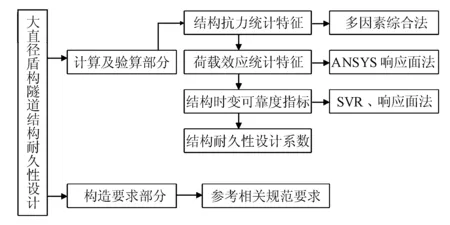
圖1 大直徑盾構隧道襯砌結構耐久性設計流程圖

2 大直徑盾構隧道襯砌結構耐久性計算

2.1 襯砌結構抗力衰減統(tǒng)計特征

盾構隧道管片結構，其受力形態(tài)一般為偏心受力。近年來，國內(nèi)外學者對銹后鋼筋混凝土構件的承載力進行了大量的研究，研究結果表明，鋼筋銹蝕對構件承載力的影響主要體現(xiàn)在3個方面：①鋼筋截面積的減小；②鋼筋屈服強度的降低；③鋼筋與混凝土之間黏結性能的退化。考慮以上3個方面，本文在計算鋼筋銹蝕后隧道襯砌結構抗力時，分別引入3個損傷系數(shù)[6]，分別反映鋼筋銹蝕引起的鋼筋截面損失及強度降低、混凝土截面損傷、鋼筋和混凝土間黏結力下降三方面的損傷效應。

因為結構抗力是隨服務年限的增加不斷降低的，所以將損傷系數(shù)看成隨機變量。同時考慮混凝土強度、鋼筋強度、鋼筋銹蝕率等隨機變量，從而求得隧道襯砌結構抗力衰減計算模型。

根據(jù)可靠度原理，隨機變量的統(tǒng)計特征為均值和標準差。通過計算結構的各隨機變量參數(shù)的統(tǒng)計特征，可得到小偏心受壓襯砌結構抗力R(t)統(tǒng)計特征見式(5)。

μRN(t)=RN(t)|μ

(5)

(6)

式中：μRN(t)為結構抗力平均強度；σRN(t)為結構抗力標準差。

2.2 荷載效應S(t)統(tǒng)計特征

對大直徑盾構隧道襯砌結構而言，由于其受力變形的機理相當復雜，且缺少基本變量的統(tǒng)計資料，因此幾乎不能采用解析法求得作用效應的顯式解。針對這些問題，國內(nèi)外已進行了大量的工作，目前通用的做法是采用隨機有限元法，該方法概念明確，計算量少，但需要對確定性有限元程序進行改造，且對高度非線性問題，存在較大的計算誤差。為解決以上問題，張彌等[7]首先將響應面法引進到隧道結構可靠度分析中，用以計算襯砌結構的荷載效應。

本文主要采用傳統(tǒng)的有限元響應面法，將結構高度的隱式非線性極限狀態(tài)方程用一個簡單的響應面函數(shù)進行替代，即建立荷載效應與隨機變量之間的一個顯式表達式，然后以該顯式表達式作為響應面函數(shù)，利用Monte-Carlo方法進行抽樣計算，最后得到荷載效應的統(tǒng)計特征。

計算襯砌結構荷載效應的統(tǒng)計特征主要是利用ANSYS計算軟件中的可靠度計算模塊，首先利用“荷載-結構”法生成可靠度分析文件，然后利用中心點復合設計擬合大直徑盾構隧道襯砌管片結構截面上彎矩和軸力的響應面方程，最后利用Monte-Carlo方法進行抽樣計算，最后得到該截面彎矩和軸力的均值和方差。

以某大直徑盾構隧道為例，隧道的外徑為14.5 m、內(nèi)徑為13.3 mm，選取江中埋深約17.5 m處襯砌管片單位寬度進行荷載效應的統(tǒng)計特征計算，用響應面法擬合截面上的彎矩和軸力的表達式，并進行敏感性分析。因荷載效應影響因素較為復雜，所以本文只將幾個主要參數(shù)看成隨機變量，其余參數(shù)假定為定值，主要參數(shù)的統(tǒng)計特征[8]見表1。

表1 影響襯砌結構荷載效應隨機參數(shù)統(tǒng)計特征表

通過“荷載-結構”法，荷載取隧道上覆水土壓力，按松散土壓力理論計算，得到該截面的襯砌結構內(nèi)力圖見圖2。

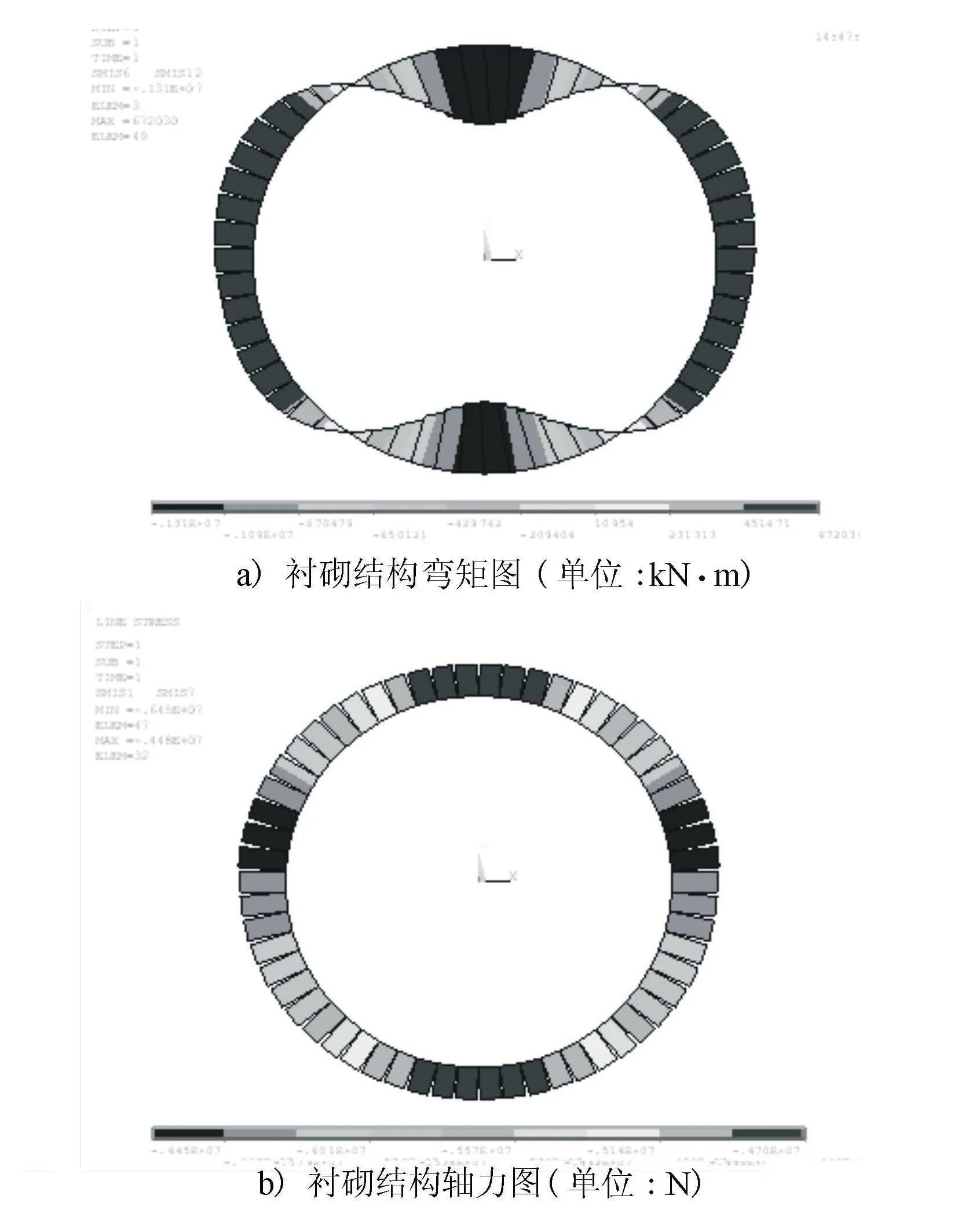
圖2 襯砌結構內(nèi)力圖

根據(jù)圖2的計算結果提取軸力(受壓)的最大值，利用ANSYS有限元的可靠度分析模塊，基于響應面法計算襯砌結構軸力的均值和標準差，其襯砌結構軸力分布圖見圖3。

圖3 襯砌結構軸力分布圖

由圖3可見，襯砌結構軸力的均值為μN=6 442.2 kPa，標準差為σN=32.942 kPa。

根據(jù)響應面有限元計算，對軸力影響因素：管片混凝土彈性模量E、管片混凝土密度DENS、管片厚度H、地基彈性抗力系數(shù)K4個輸入隨機變量進行敏感性分析，顯著性水平2.5%下，軸力影響因素敏感性分析結果對比餅狀圖見圖4。

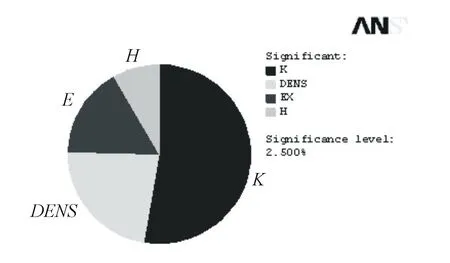
圖4 軸力影響因素敏感性分析圖

由圖4可見，對于影響軸力的4個隨機因素中，地基彈性抗力系數(shù)對襯砌結構軸力的影響是最大的，其次是管片密度、彈性模量和管片厚度。

2.3 襯砌結構時變可靠度指標計算

大直徑盾構隧道襯砌結構極限狀態(tài)方程是高度非線性的，直接采用一般的可靠度計算方法得到的是幾何可靠度，存在較大誤差，需進行改進。可采用基于結構風險最小化原理的支持向量機回歸(SVR)和響應面法相結合的方法，利用支持向量機回歸對小樣本數(shù)據(jù)良好的學習和泛化能力，用SVR重構結構響應面方程建立基于SVR和響應面結合的結構時變可靠度的計算方法。

通過結合室內(nèi)試驗和經(jīng)驗公式得到結構原始極限狀態(tài)方程及其參數(shù)的統(tǒng)計特征，通過二次規(guī)劃，得到利用支持向量回歸機重構的響應面極限方程，以響應面方程作為近似功能函數(shù)進行抽樣，考慮抗力衰減的時變性，從而計算結構的時變可靠度。主要流程如下。

1) 假定初始迭代點x(t)=[x1(t),x2(t),…,xn(t)]T，一般取平均值μX(t)。

2) 通過結構數(shù)值分析或試驗在各個展開點處計算功能函數(shù)的估計值gi(t)(i=1,2,…,2n+1)，并形成相應的系數(shù)矩陣。

3) 將上述2n+1個樣本點作為訓練樣本集，并對輸入樣本和輸出樣本進行數(shù)據(jù)歸一化處理。

4) 根據(jù)輸入和輸出樣本，利用交叉驗證法和試算法選擇最優(yōu)的SVR參數(shù)C和r。

5) 構造核函數(shù)K矩陣，將歸一化后的2n+1個樣本點代入非線性求解問題的內(nèi)積核函數(shù)，求解二次規(guī)劃問題，求得拉格朗日乘子及常數(shù)項b的數(shù)值，從而求得SVR響應面方程式。

6) 通過SVR響應面方程求得設計驗算點和可靠度指標，并判斷其變化幅度。

|βk(t)-βk-1(t)|是否滿足所需精度，若不滿足，則返回第(3)步，重新開始迭代計算。

7) 根據(jù)可靠度指標與失效概率、耐久性系數(shù)之間的轉換關系，分別求出結構服務年限內(nèi)失效概率與耐久性系數(shù)。

2.4 襯砌結構時變可靠度指標計算

基于上述程序理論，對某大直徑盾構隧道襯砌結構進行耐久性設計，利用MATLAB軟件，計算結構的時變可靠度指標及失效概率，從而計算結構耐久性設計系數(shù)η(t)和結構安全系數(shù)，當?shù)竭_結構100年服務壽命時，確定其對應的耐久性設計系數(shù)，從而據(jù)此建立隧道襯砌結構耐久性設計的極限狀態(tài)方程見式(7)。

γ0S≤η(100)R

(7)

式中：γ0為結構重要性系數(shù)，本文取1.1；S為100年服務壽命內(nèi)襯砌結構的軸力，本文取初始軸力的均值；η(100)為100年服務壽命時襯砌結構耐久性設計系數(shù)，根據(jù)程序進行計算；R為100年服務壽命時襯砌結構抗力，按程序進行計算。

依據(jù)以上極限狀態(tài)方程可以改進隧道襯砌結構設計，從而確保隧道襯砌結構主體結構的設計使用年限的順利實現(xiàn)。實例計算如下。

隧道盾構管片環(huán)寬2 m，管片厚度60 cm，采用雙面楔形形式。管片混凝土標號C60，保護層厚度為50 mm。

計算結構失效概率、結構可靠度指標、結構耐久性設計系數(shù)圖，結果見圖5～圖7。

圖5 某大直徑盾構隧道襯砌結構失效概率計算圖

圖6 某大直徑盾構隧道襯砌結構可靠度指標計算圖

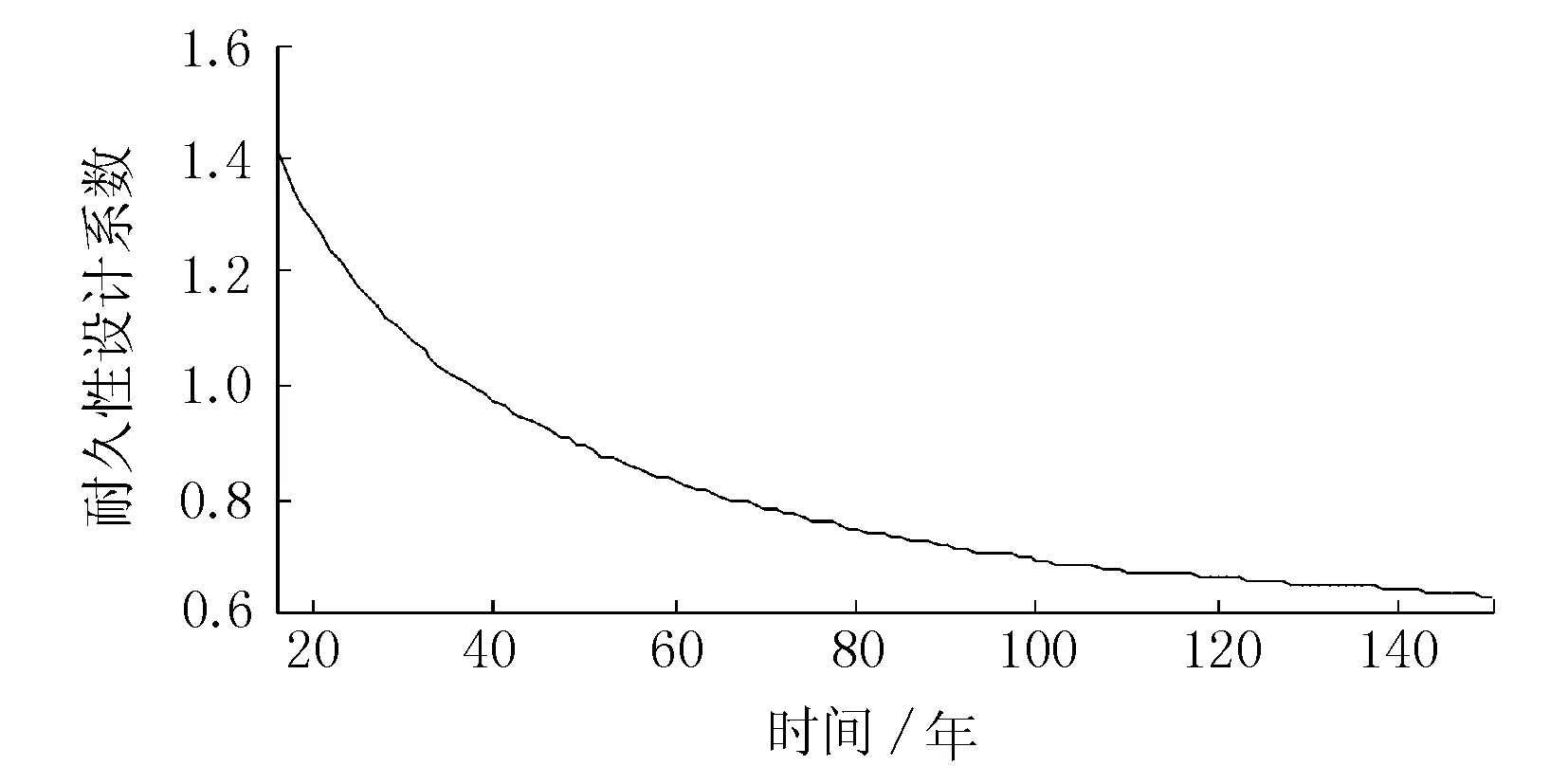
圖7 某大直徑盾構隧道襯砌結構耐久性設計系數(shù)計算圖

從圖5～圖7中可知，某大直徑盾構隧道建成投入使用100年后，隧道襯砌結構可靠度指標為2.047 7，耐久性設計系數(shù)為0.691 3，失效概率為2.03%，滿足GB/T 50476-2019 《混凝土結構耐久性設計標準》失效概率不大于5%～10%的要求，說明盾構隧道100年的設計使用年限可以得到保證。同時由100年后耐久性設計系數(shù)，可以建立大直徑盾構隧道襯砌結構耐久性設計的極限狀態(tài)方程如式(8)。

γ0S≤0.693 1R

(8)

根據(jù)極限狀態(tài)方程的計算，可知某大直徑盾構隧道襯砌主體結構能滿足結構100年服務壽命的要求。

3 結論

本章通過采用支持向量機(SVR)與響應面相結合的方法作為大直徑盾構襯砌結構耐久性設計的計算方法，基于可靠度理論，利用MATLAB計算軟件，并在某大直徑盾構隧道耐久設計中得到了應用，主要工作及研究成果如下。

1) 在對比傳統(tǒng)耐久性設計方法和相關規(guī)范規(guī)定的不足之后，利用SVR和響應面相結合的原理，給出了大直徑盾構襯砌結構耐久性設計的基本步驟，利用MATLAB編程軟件進行計算。

2) 通過建立結構抗力和結構作用效應之間的極限狀態(tài)方程，從而計算結構時變可靠度指標和失效概率，進而計算結構耐久性設計系數(shù)，進行耐久性設計。

3) 通過ANSYS計算軟件中的可靠度計算模塊，先根據(jù)“荷載-結構”法計算結構的內(nèi)力，然后進行響應面模擬，得到結構內(nèi)力的均值和方差，并進行影響結構內(nèi)力的參數(shù)敏感性分析。

4) 用SVR重構結構響應面方程，建立了基于SVR和響應面結合的結構時變可靠度的計算方法。利用MATLAB軟件編制了大直徑盾構隧道襯砌結構在服務壽命期限內(nèi)的時變可靠度指標及其失效概率的計算程序。

5) 根據(jù)耐久性設計系數(shù)與時變可靠度指標的相互關系，計算隧道襯砌結構達到100年服務壽命時的耐久性設計系數(shù)，得到某大直徑盾構隧道襯砌結構100年服務壽命時的極限狀態(tài)方程：從而得到某大直徑盾構隧道襯砌結構滿足100年服務壽命的結果。